包含混合过程的理想气体pVT变化导致的熵变计算

杨汉培 岑 程 吴俊明

(河海大学浅水湖泊综合治理与资源开发教育部重点实验室，河海大学环境学院，江苏 南京 210098)

包含混合过程的理想气体pVT
变化导致的熵变计算

杨汉培 岑 程 吴俊明

(河海大学浅水湖泊综合治理与资源开发教育部重点实验室，河海大学环境学院，江苏 南京 210098)

针对包含混合过程的理想气体pVT变化导致的熵变计算，现行教材中推荐的计算方法对气体体积V及压力p的使用易在总量或分量上产生混淆。本文探讨了一种分步计算方法，以使初学者深入理解包含混合熵的理想气体pVT变化导致的熵变计算，为该知识点的教与学提供有益参考。

熵 熵变计算 混合 理想气体

熵是一个重要的热力学函数，抽象、难懂。熵变的计算理论性强、公式繁多且限制条件严谨，初学者不易掌握，系教学中的难点[1]，尤其对包含混合过程的理想气体状态变化的熵变计算，学生在相关公式的运用中常存在困惑[2]，因此，积极实行新的教学尝试，以引导学生正确理解理想气体混合熵变及计算十分必要。

1 理想气体pVT变化熵变的一步法计算

对于理想气体单纯pVT变化导致的熵变计算，无论过程可逆与否，状态变化(p1V1T1→p2V2T2)的熵变均可按下列所示的式1或2计算[3]，式中Cv,m及Cp,m分别为理想气体的等温和等压摩尔热容。

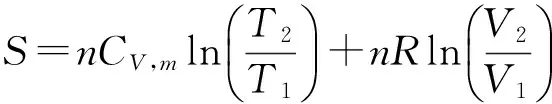
(1)

(2)

对于包含了混合过程的理想气体pVT变化导致的熵变计算，在运用式1或2时需在总压(体积)或分压(分体积)间正确选择，这常令初学者困惑，进而不能明确理想气体混合熵变的真正含义。以具体的习题求解为例[4]：

绝热恒容容器中有一绝热耐压隔板，一侧为2 mol的200 K，50 dm3的单原子理想气体A，另一侧为3 mol的400 K，100 dm3的双原子理想气体B。今将器中的绝热隔板撤去， 气体A与气体B混合达到平衡态，求过程的⊿S。

运用式(1)计算时，文献推荐的求解方法为[5]：

先解出末态温度T。绝热恒容混合过程：Q= 0，W= 0，⊿U=Q+W= 0, 即：

⊿U=nACV, m(A)(T-TA1) +nBCV, m(B)(T-TB1) = 0

⊿S= ⊿S(A) + ⊿S(B)

撤去挡板后，平衡时A、B两气体将充分混合并均占有整个容器，故VA2、VB2均应取总体积，即容器体积V(150 dm3)。由此可见，上述计算的结果已包含了理想气体混合过程的熵变。

若以式(2)计算，由理想气体普适方程pBV= nBRT(B为任何理想气体)，可分别求得混合前A、B气体的分压：

pA1= 66.51 kPa ,pB1= 99.77 kPa。

根据道尔顿分压定律可知，混合体系中气体的分压对应总体积，因此：

pA2= (nART)/VA2= (2×8.314×342.86)/(150×10-3) = 38.01 kPa，

同理，pB2= 57.01 kPa。

上述各数据代入式(2)，可得：

⊿S= ⊿S(A) +⊿S(B)

2 理想气体pVT变化熵变的两步法计算

由上述计算可见，直接运用式1或2，虽步骤简便，但需对式中压力或体积的总量和分量作出正确选择，同时，这种“黑箱式”的求解，也阻碍了学生对混合熵这一知识点的认识。为此，尝试此类问题的两步法求算。

设计一个中间状态2，同时将1中隔板虚拟为一种耐压导热隔板以平衡两侧气体温度和压力而气体分子无法通过，如此，上述过程可视为经历了两个各自独立的过程。

过程1：A、B两种气体经由各自pVT变化到达其平衡态(状态2)。

参见2的计算过程，求得TA2=TB2= 342.86 K

因pA2=pB2，则VB2/VA2= nB/nA= 3/2。

计算出：VA2= (2/5)×150 = 60 dm3,VB2= (3/5)×150 = 90 dm3。

运用式(1)，可得：

⊿S12=⊿S12(A) + ⊿S12(B)

同理，运用式(2)也能到相同的结果。

由于此时隔板还未撤除，不存在气体混合，因此无需在总量或分量上区分。

过程2：等温、等压下两种气体混合并达到其平衡态(状态3)。

根据理想气体混合及其混合熵的定义[6]，恒温下，各气体组分单独存在时的压力都相等且又等于混合后的总压力时，从每种气体各自独立存在至混合存在的过程称为混合，对应的熵变称为混合熵，其计算公式如式(3)所示[7]：

(3)

式中yB为任意气体组分的摩尔分数。

上述公式不仅适用于理想气体，对理想溶液的混合熵计算也同样满足。这一关键知识点，可以在分步计算的解题过程中有所体现。

即⊿S23= ⊿Smix= -8.314×(2ln(2/5) + 3ln(3/5)) = 27.98 J·K-1

⊿S13= ⊿S12+ ⊿S23= (4.24 + 27.78) J·K-1= 32.22 J·K-1。

3 结 论

实际教学中，可尝试将两种方式结合和对比以阐明，一步法计算步骤简便，但易在公式中的p或V的总量及分量间混淆，而两步法处理，可在前一步避免计算通式中的p或V总量与分量间的混乱，同时在后一步指明隐含的不同理想气体间的混合过程实质及其混合熵的计算，强化学生对于理想气体混合的概念及混合熵计算公式的应用，使模糊的过程具体化，避免学生的不确定感和可能导致的陌生感和厌学情绪。

[1] 王金艳.哈尔滨师范大学自然科学学报[J].2005,21(5):38～40.

[2] 岳凡,陈华梅,孙都成.关于理想气体混合熵变的讨论[J].大学化学,2013,28(1):61～63.

[3] 刘俊吉,周亚平,李松林.物理化学[M].上册.北京:高等教育出版社.5版,2012,109.

[4] 刘俊吉,周亚平,李松林.物理化学[M].上册.北京:高等教育出版社.5版,2012,146.

[5] 冯霞,高正虹,陈丽.物理化学解题指南[M].北京:高等教育出版社.2版,2013,73～74.

[6] 傅献彩,沈文霞,姚天扬.物理化学[M].上册.北京:高等教育出版社.4版,2001,113.

[7] 周鲁.物理化学教程[M].北京:科学出版社.3版,2012,55.

CalculationfortheEntropyChangesintheVariationofpVTofPerfectGasesInvolvingtheGasMixture

Yang Hanpei Cen Cheng Wu Junming

(Key Laboratory of Integrated Regulation and Resource Development on Shallow Lakes, Ministry of Education, College of Environment, Hohai University,Jiangsu Nanjing 210098)

For the calculation of the entropy changes in the variation ofpVTof perfect gases, most of the textbooks recommended a general formula and its variation form，which usually confuse the total and partial pressure (volume) in the formula. In this paper, a two step-treatment including the calculation for the mere state change and mixing of gases was proposed, respectively, to avoid the aforesaid confusion and contribute to their intensively understanding in calculation of entropy changes resulted by mere state change or gas mixture. The attempt provided a helpful reference in teaching and learning for the required knowledge.

entropy calculation of the entropy change mixture perfect gas

10.16597/j.cnki.issn.1002-154x.2017.03.005

2017-02-20

江苏省高校优势学科建设工程资助项目。

杨汉培(1964～)，男博士，教授，主要研究方向：现代水处理技术，E-mail：yanghanpei@hhu.edu.cn。