非等晕效应对NVST高分辨重建结果的影响*

李茂林，向永源 ，金振宇，刘 忠

(1. 中国科学院云南天文台，云南 昆明 650011；2. 中国科学院大学，北京 100049)

大气湍流将地基大望远镜的成像分辨率限制在1″左右，实时补偿的自适应光学技术和高分辨图像处理方法能够克服大气湍流的影响，实现地基望远镜衍射极限成像[1]。一些已经应用于太阳望远镜的高分辨图像处理方法主要有斑点重构法、相位差法、太阳多帧盲反卷积法。对于斑点重构法，比如斑点干涉术(Speckle Interferometry)、KNOX-THOMPSON算法和斑点掩模法(Speckle Masking)，只在等晕区内有效。等晕区内部近似是一个线性空不变系统，可认为具有相同的点扩展函数(Point Spread Function, PSF)。天文上一般一个等晕区大小不超过5″。通常，大视场目标的高分辨图像重建，图像需要分块重建，分块的原则是子块大小和等晕区大小匹配[2]。当重建区域大于等晕区时，不再满足线性空不变条件，大气的非等晕效应使斑点重构算法失效。

抚仙湖1 m新真空太阳望远镜(New Vacuum Solar Telescope, NVST)是国内口径最大的地基真空太阳望远镜，主要用于太阳光球和色球的高分辨率成像观测和太阳光谱观测[3-4]。1 m太阳望远镜目前采用斑点干涉术和斑点掩模法的图像统计重建技术对观测图像进行高分辨率重建[5]，重建子块大小为4.5″，是根据经验值确定的。真实的等晕区大小与大气状况有关，在观测过程中，很难精确知道等晕区的大小，这就导致在图像重建过程中子块大小不够精确。显然，以固定的经验值分块重建存在算法失效造成重建精度降低的可能性，比如会导致光球磁亮点与米粒间对比度降低，磁亮点分辨率下降。

已经有研究人员做过很多关于大气非等晕效应的研究，比如，文[6]使用数值模拟的方法分析非等晕性对斑点图功率谱的影响；文[2]通过双星的斑点图和斑点干涉术方法研究大气的非等晕性；文[7]使用斑点全息术(Speckle Holography)测量等晕区的大小；文[8]研究非等晕效应对KNOX-THOMPSON算法的影响。本文基于1 m太阳望远镜实测数据，采用斑点重构方法，展开对望远镜不同重建子块大小情况下非等晕效应的影响分析。

1 理论分析

斑点重构方法完整的重建目标，需要分别重建目标的傅里叶模(斑点干涉术)和傅里叶相位(斑点掩模法或KNOX-THOMPSON算法)。大视场目标图像分块重建时，如果分块大小超过真实的等晕区大小，重建结果的模和相位均可能存在因算法失效引起的误差。下面以两个点源目标为例，理论上推导大气非等晕性对模和相位重建算法的影响。

1.1 等晕区

观测时，因目标各部分的光传输路径不同，各部分的瞬时点扩展函数也不一样，但是一定视场范围内，各个小区域基本满足线性空不变假设，有相同的点扩展函数，这个区域称为等晕区。如图1，来自不同方向上的目标O1和O2的光束经历了不同的大气扰动，当两个目标靠得比较近时(比如1″、 2″)，可以认为这两个目标经历了相同的大气扰动，也可以认为在同一个等晕区内。图中虚线矩形框内为两个目标经历的相同的大气扰动，可以看出两个目标越靠近，经历的大气扰动相关性越大。根据文[9]的研究，对于Kolmogorov湍流，大气等晕角可表示为

(1)

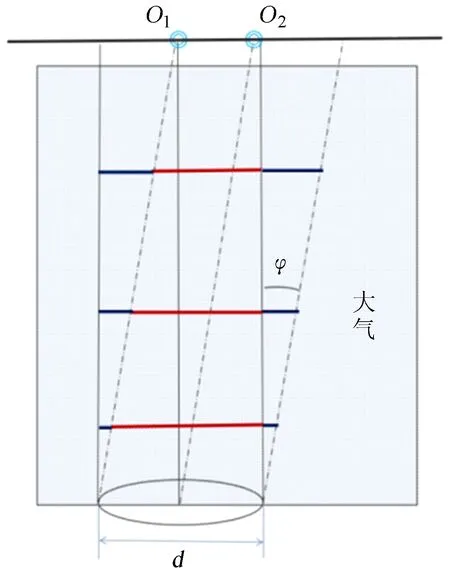
图1 等晕区示意图
Fig.1 The diagram of isoplanatic region

1.2 非等晕效应对斑点干涉术的影响

斑点干涉术由文[10]提出，是通过统计斑点图的平均能谱复原目标傅里叶振幅。在满足等晕性假设的条件下，每帧短曝光图像i(x,y)可以看作是目标o(x,y)和系统点扩展函数h(x,y)的卷积：

i(x,y)=o(x,y)⊗h(x,y) .

(2)

对斑点图进行能谱统计并引入遍历性假设后，目标功率谱可写为

(3)

其中，〈〉表示算术平均；I(u,v)，O(u,v)，H(u,v)为(2)式对应项的傅里叶变换；分母叫做斑点干涉术传递函数(Speckle Transfer Function, STF)。

假设两个角距离为θ的点源分别为m1δ1(x,y)，m2δ2(x,y,θ)，其中m1，m2为点源强度，通过大气不同部分成像时瞬时点扩散函数分别为h1(x,y)，h2(x,y,θ)，则斑点图强度为

ix,y=m1δ1x,y⊗h1x,y+m2δ2x,y,θ⊗h2x,y,θ，

(4)

在满足遍历条件下，斑点图平均功率谱为

〈I(u,v)2〉=m12〈H1u,v2〉+m22〈H2u,v,θ2〉+

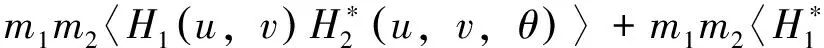
(5)

从(5)式可以看出，当θ足够小，两个目标在等晕区内，即H1(u,v)=H2(u,v,θ)时，(5)式简化为

〈I(u,v)2〉=m1+m22〈H1u,v2〉，

(6)

对(6)式退卷积可得目标的强度；当H1(u,v)≠H2(u,v,θ)时，不论使用哪个点源目标的斑点干涉术传递函数都无法准确得到两个目标的强度。因此，重建区域超过等晕区大小时，大气的非等晕效应导致斑点干涉术算法失效，算法失效使得目标的傅里叶模重建不准确。

1.3 非等晕效应对斑点掩模法重建相位的影响

斑点掩模法由文[11]提出，又称为三重相关法或重谱法，是对目标斑点图的三重相关进行统计平均。使用重谱法可以从统计结果中递推出重建目标的相位。函数i(x,y)的重谱表达式为

I(3)(u,v,Δu,Δv)=I(u,v)I(Δu,Δv)I*(u+Δu,v+Δv)，

(7)

为了简化，将(7)式写成如下形式：

(8)

在满足等晕条件和遍历假设的前提下，斑点图的重谱统计为

(9)

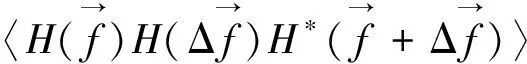
(10)

按照湍流大气理论，波相位的涨落服从高斯分布，根据对于任何实值高斯随机变量z和任何复常数a都成立的关系：

(11)

则：

(12)

(12)式所得结果为实数，可以说明(9)式中和传递函数相关的部分为实数，对重谱的相位没有贡献。

根据(9)式重谱相位和目标的相位关系可以写为

(13)

其中，ΦB为重谱对应的相位；φ为目标对应频率的傅里叶相位。根据(13)式可以从低频到高频递推目标的全部相位。

1.2节两个点源目标斑点图的重谱统计为

根据(11)式可证明(14)式中和传递函数相关的部分均为实数，传递函数对重谱的相位并没有贡献。虽然传递函数相关项不会影响重谱的相位，但是当扩展目标超过等晕区大小时，目标重谱相位与目标傅里叶相位之间的关系不再严格满足(13)式。因此，当重建区域超过等晕区大小时，非等晕效应导致目标相位与重谱相位不再满足相位递推关系，在使用斑点掩模法递推目标傅里叶相位时会出现误差，随着递推频率的增加，递推误差不断累积。

2 数据分析

2.1 数据重建流程简介

1 m太阳望远镜数据处理简要的流程图如图2，主要包括数据预处理、图像分块、振幅和相位重建以及图像拼接。其中数据预处理包括平暗场处理、数据对齐。图像分块应尽量使重建区域在等晕区大小以内。1 m太阳望远镜使用斑点干涉术复原目标各子块的傅里叶模，使用斑点掩模法重建目标各子块的傅里叶相位。重建各子块振幅和相位之后合成复变量，再通过逆傅里叶变换得到高分辨率的子图像，然后各子图像拼接成全视场图像[1]。

2.2 数据重建

理论上分析了当重建区域超过等晕区大小时非等晕效应会使算法失效，造成目标傅里叶模和相位重建准确度降低，接下来通过对模和相位的分析研究在实际数据处理中不同重建子块大小情况下非等晕效应对算法重建结果的影响。

2.2.1 实测数据

使用1 m太阳望远镜的实测光球数据分别进行分块重建，数据取自2014年10月3日。光球数据使用Andor sCMOS相机采集，波段为705.8 nm，采集图像大小2 560 × 2 160 pixel，每组200帧，采集时间30 s。数据分块重建区域大小分别为5″、10″、15″、20″。图3为其中一张原始数据图。

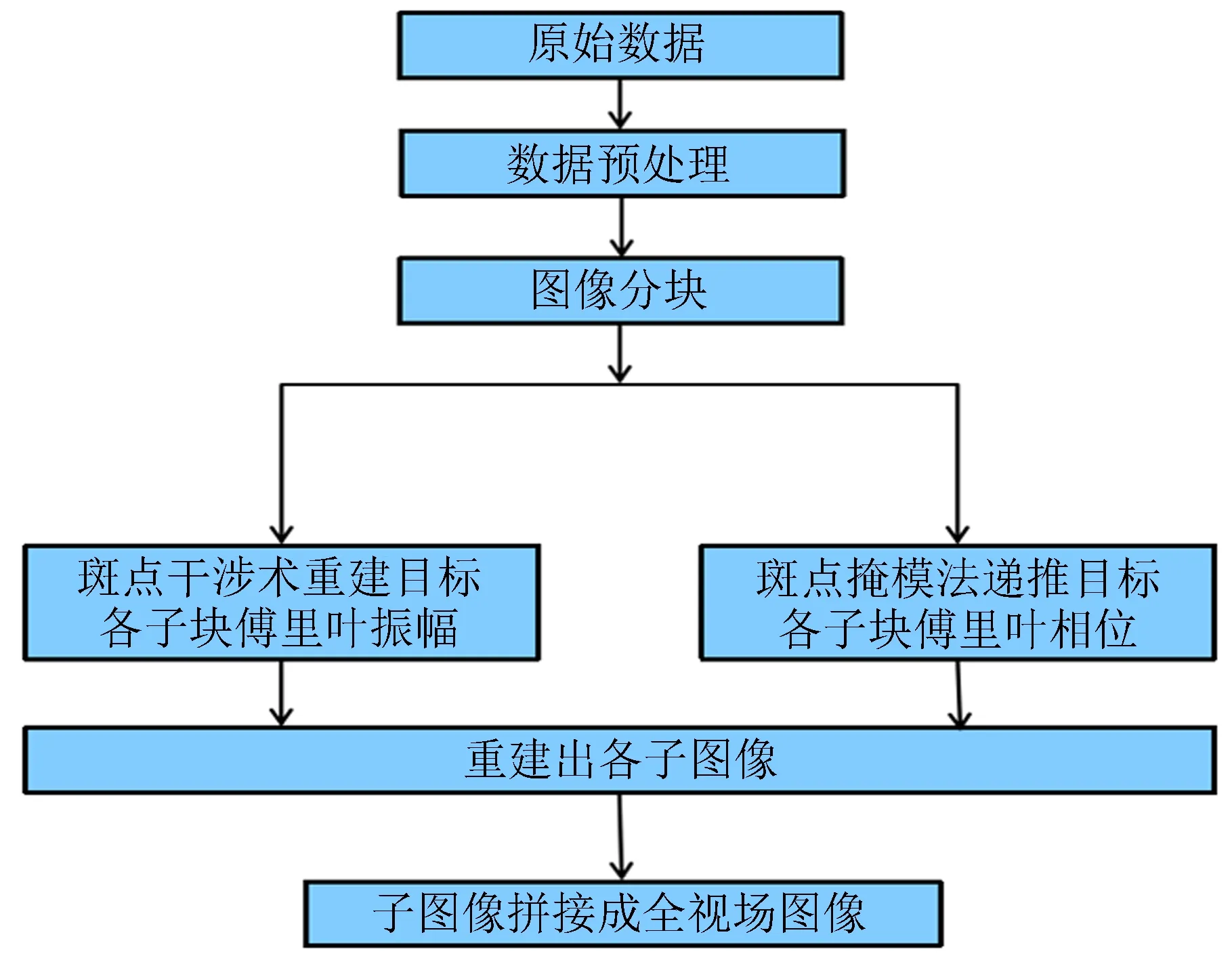
图2 数据处理简要流程图
Fig.2 Flow diagram of data processing

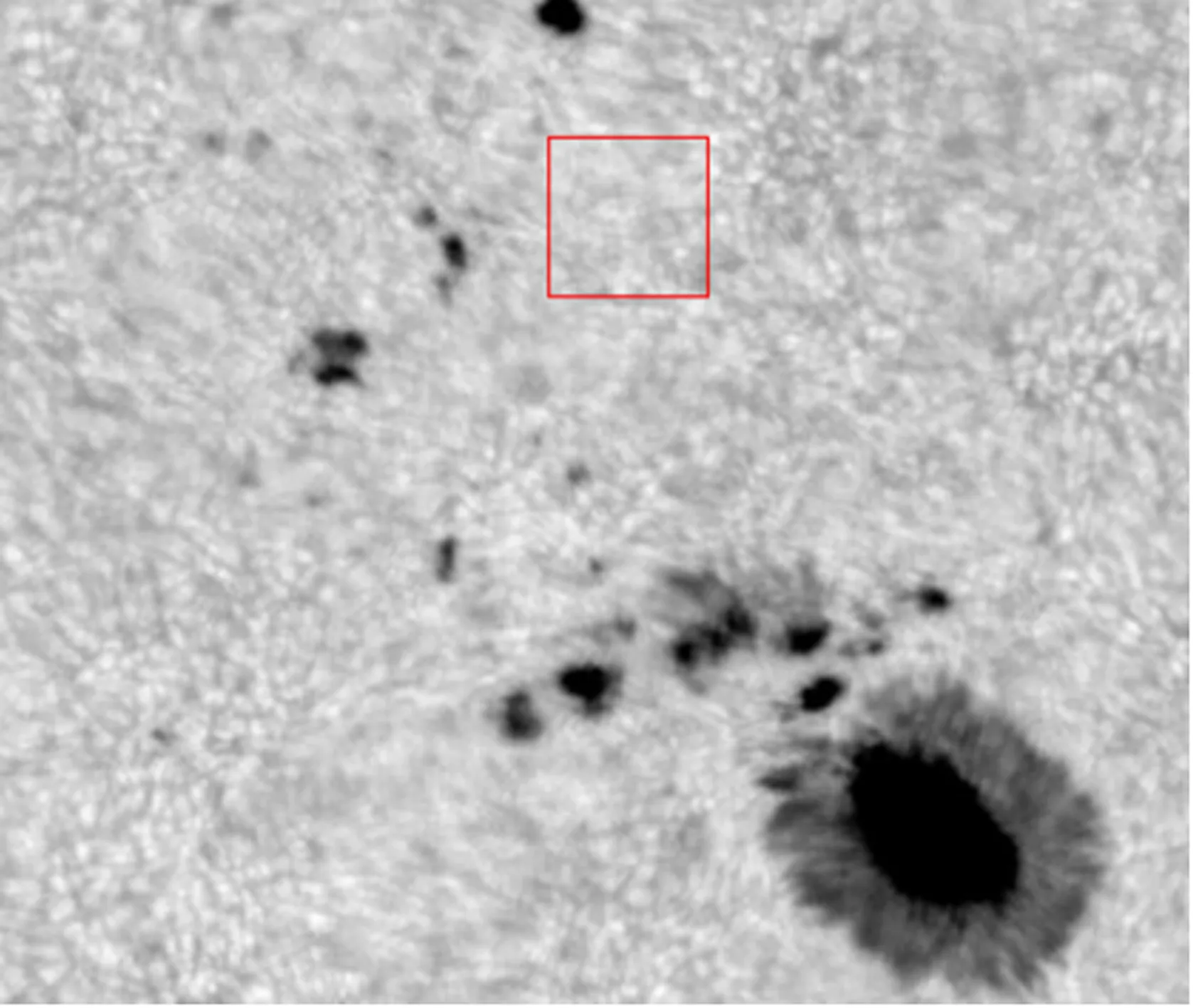
图3 原始数据图
Fig.3 The raw data

2.2.2 重建结果

由于重建图像过大，这里只取图3中红色框部分进行比较，图4为红色框部分对应的重建结果。从上至下、从左至右重建子块大小分别为5″、10″、15″、20″。

通过对不同结果的比较，可以发现，5″ 重建结果分辨率最高，图像质量最好。当子块大小为10″ 时，5″ 重建结果中米粒间部分相近的孤立磁亮点在10″ 重建结果中表现为长链式结构，并且磁亮点与米粒结构的对比度有所降低。15″ 和20″ 重建结果中图像分辨率明显降低，图像质量明显下降。

2.3 重建结果分析

从图4的重建结果可以看出，随着重建子块大小的增加，图像质量明显下降，接下来对重建图像的功率谱和相位做进一步分析。

2.3.1 功率谱分析

图像f(x,y)的功率谱可由其傅里叶变换模的平方得到，(15)式为图像功率谱表达式：

PSu,v=FFTfx,y2.

(15)

从(15)式可以看出，图像功率谱并不包含图像的傅里叶相位，只反映重建图像模的情况。

图5为重建结果的功率谱曲线图，为了方便分析，这里只给出3条曲线。图中实线、实线加“*”、虚线分别对应5″、15″、20″ 情况下重建图像的平均功率谱曲线。

通过功率谱图可以看到，重建分块的大小在低频部分对图像功率谱没有太大影响，影响比较大的是中频附近至高频部分。15″ 功率谱曲线中频、高频均低于5″ 的情况，在中频、中高频区域下降比较明显，说明图像的对比度、分辨率已经有变化。20″ 的功率谱曲线在中频附近低于15″ 的功率谱曲线，其它部分都很接近。对10″ 重建结果的功率谱进行了分析，发现10″ 和5″ 的功率谱曲线在低频部分非常接近，但是在中频至中高频部分，10″ 的功率谱曲线整体低于5″ 的功率谱曲线。随着重建子区域的增大，重建图像功率谱曲线之间的差距在减小且这种差距有向中频集中的趋势。

图4 数据重建结果，从上至下、从左至右重建区域大小分别为5″、10″、15″、20″

Fig.4 Data reconstruction results and from top to bottom, from left to right the reconstruction sub-fields size are 5″, 10″, 15″, 20″

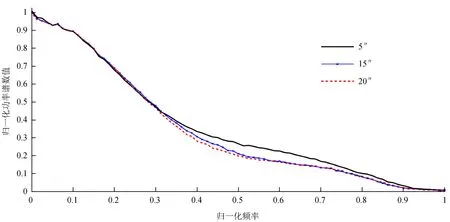
图5 图像功率谱曲线图
Fig.5 The curve of power spectrum

2.3.2 相位分析

相位和模共同决定重建图像的质量，为了看出相位对图像质量的影响，这里使用固定的模和重建的相位组合的方法。固定的模采用重建子区域为5″ 时得到的结果，和重建子区域大小为10″、15″、20″ 时得到的对应区域的相位分别组合得到的部分图像如图6。图6代表的区域与图4一致，从左至右采用的相位分别对应10″、15″、20″。

图6 固定的模与不同相位的组合结果，从左至右重建区域大小分别为10″、15″、20″

Fig.6 The results of fixed amplitude combine with different phases and from left to right the reconstruction sub-fields size are 10″, 15″, 20″

从图6可以看出，随着重建子区域的增大，图像质量逐渐下降且都低于图4中5″ 的情况。由于使用的模相同，图像质量的下降是由相位重建准确度降低引起，通过图像质量的比较可以知道，4种情况下重建子区域为5″ 时相位重建的准确度最高，最接近目标的真实相位。

将图6中10″、15″、20″ 重建的相位写成复指数形式与5″ 对应区域重建相位的复指数形式相减，并求出相减结果的模。(16)式为计算公式：

Z=expjΦm-expjΦ5″，

(16)

其中，||表示求复数的模；Φ5″为5″ 重建的相位；Φm为10″、15″、20″ 重建的相位。

经过计算得到图7的指数相位相减图，从左至右分别为10″、15″、20″ 与5″ 相同区域重建相位的复指数形式相减结果的模。从图7可以发现，10″、15″、20″ 情况下重建的中高频部分的相位与5″ 时均有差别，且随着重建子区域的增加中间低频部分差别也在增加。随着重建子区域的增大，相位重建准确度降低。

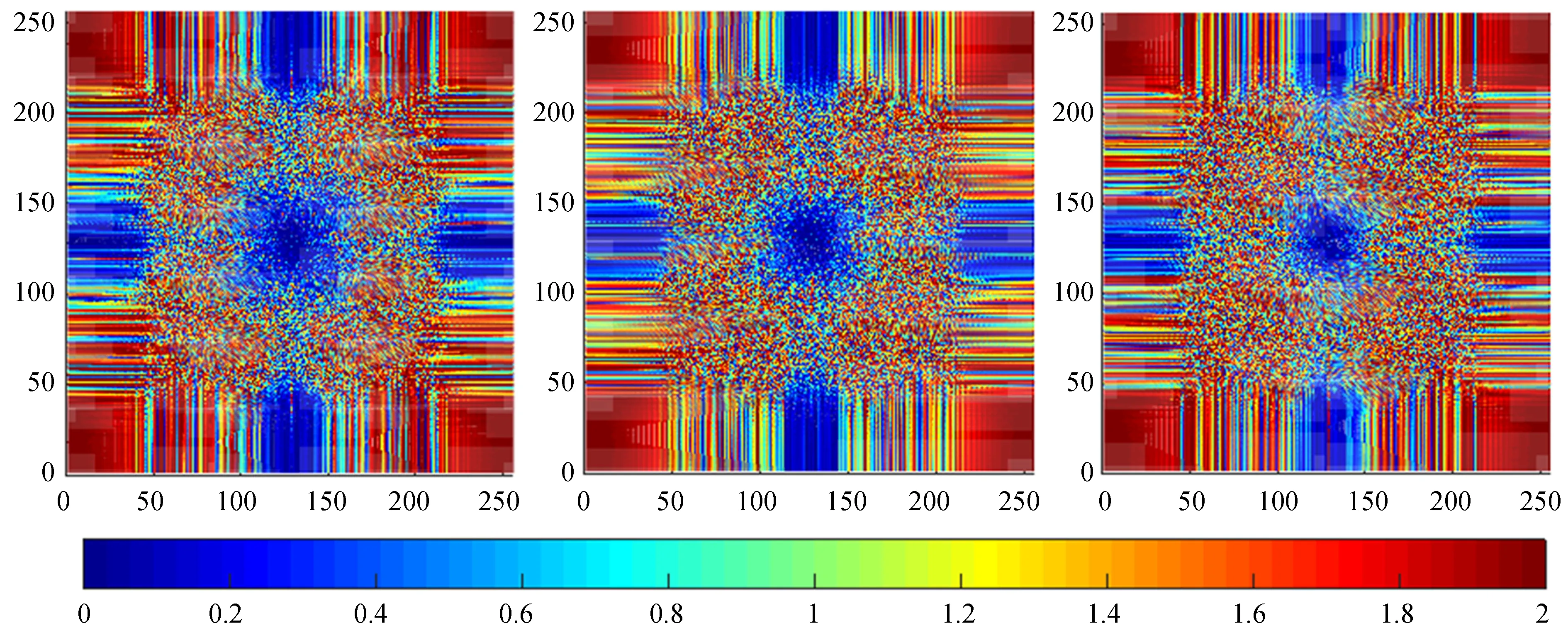
图7 相位相减结果图,从左至右对应重建区域大小分别为10″、15″、20″
Fig.7 The image of phase subtraction result and from left to right the reconstruction sub-fields size are 10″, 15″, 20″

3 讨论与总结

当重建子区域大小为10″、15″、20″ 时已经超过天文上一个等晕区大小，此时非等晕效应使斑点干涉术和斑点掩模法失效，算法重建的傅里叶模和相位准确度的降低导致图像分辨率降低，细节不丰富。通过以上分析可以知道，不同子块大小重建结果有差别，图像质量随着子块大小的增加而下降。说明重建子块越大，超过等晕区大小越多时，非等晕效应对斑点干涉术和斑点掩模法的影响越严重。

为了重建图像有更好的分辨率，最好以等晕区大小分块，这样非等晕效应对斑点干涉术和斑点掩模法的影响最小，甚至可以忽略。但是实时获取大气等晕区大小比较困难，分块小也未必能得到最好的结果，在上面的实测数据分块重建中，计算了子块大小2″ 时的结果，发现并没有5″ 效果好。这是因为在斑点重构之前需要对数据进行对齐以降低望远镜的晃动或者跟踪误差带来的不利影响，子块过小对齐精度降低，同样影响图像质量。

在数据处理中，分块大小要综合考虑多种因素，比如当日的大气视宁度、风速等。考虑到1 m太阳望远镜高分辨重建算法的实际情况，建议在对某一段时间的实测数据进行高分辨重建时，先采用不同子块大小重建出少量的图像。通过对不同子块大小的结果进行比较确定最合理的重建子块大小，最后再进行全部数据的高分辨图像重建。

[1] 向永源, 刘忠, 金振宇, 等. 高分辨率太阳图像重建方法[J]. 天文学进展, 2016, 34(1): 94-110.

Xiang Yongyuan, Liu Zhong, Jin Zhenyu, et al. High resolution solar image reconstruction[J]. Progress in Astronomy, 2016, 34(1): 94-110.

[2] Nisenson P, Stachnik R V. Measurements of atmospheric isoplanatism using speckle interferometry[J]. Journal of the Optical Society of America, 1978, 68(2): 169-175.

[3] 韩笑, 徐稚, 李正刚, 等. 一米新真空太阳望远镜多波段光谱仪杂散光及空间PSF的测量[J]. 天文研究与技术, 2017, 14(1): 52-59.

Han Xiao, Xu Zhi, Li Zhenggang, et al. Stray-light and space PSF measuring of the multi-band spectrometer of the 1m New Vacuum Solar Telescope[J]. Astronomical Research & Technology, 2017, 14(1): 52-59.

[4] 韩笑, 徐稚, 李正刚, 等. 一米新真空太阳望远镜多波段光谱仪CaⅡ通道杂散光研究[J]. 天文研究与技术, 2016, 13(4): 446-454.

Han Xiao, Xu Zhi, Li Zhenggang, et al. Stray-light research for the CaⅡ channel of multi-wavelength spectrometer of the 1m New Vaccum Solar Telescope[J]. Astronomical Research & Technology, 2016, 13(4): 446-454.

[5] 方玉亮, 金振宇, 刘忠, 等. 一米新真空太阳望远镜离焦对高分辨太阳观测图像重建的影响[J]. 天文研究与技术, 2015, 12(2):183-188.

Fang Yuliang, Jin Zhenyu, Liu Zhong, et al. A study of influences of defocus aberrations on high-resolution image reconstruction for data from the New Vacuum Solar Telescope of the YNAO[J]. Astronomical Research & Technology, 2015, 12(2): 183-188.

[6] Korff D, Dryden G, Leavitt R P. Isoplanicity: the translation invariance of the atmospheric Green′s function[J]. Journal of the Optical Society of America, 1975, 65(11): 1321-1330.

[7] Weigelt G P. High-resolution astrophotography. new isoplanicity measurements and speckle holography applications[J]. Optica Acta, 1979, 26(11): 1351-1357.

[8] Lühe O V D. High resolution speckle imaging of solar small-scale structure: the influence of anisoplanatism[C]// Proceedings of a Specialized Session of the Eighth IAU European Regional Astronomy Meeting Toulouse. 1985: 96-102.

[9] Fried D L. Anisoplanatism in adaptive optics[J]. Journal of the Optical Society of America, 1982, 72(1): 52-61.

[10]Labeyrie A. Attainment of diffraction limited resolution in large telescopes by fourier analysing speckle patterns in star images[J]. Astronomy and Astrophysics, 1970, 6(1): 85-87.

[11]Weigelt G P. Modified astronomical speckle interferometry “speckle masking” [J]. Optics Communications, 1977, 21(1): 55-59.