一种落角约束的自适应模糊滑模导引律

王雪梅, 邵国豪俊, 许 哲, 于 帆

(1.火箭军工程大学，西安 710025； 2.中国科学院光电技术研究所，成都 610000)

一种落角约束的自适应模糊滑模导引律

王雪梅1, 邵国豪俊1, 许 哲1, 于 帆2

(1.火箭军工程大学，西安 710025； 2.中国科学院光电技术研究所，成都 610000)

考虑末制导中的落角约束和过载约束，提出一种自适应模糊滑模导引律，并采用李雅普诺夫稳定性判据对其稳定性进行了证明。通过将落角与视线角联系起来，从而设计滑模面实现落角约束。通过引入自适应模糊推理系统消除滑模控制中的抖振，提高了导引律的实用性。由于模糊推理具有强大的自学习能力，可在线修正加速度指令，故而对于未知干扰和模型不确定性具有良好的鲁棒性，提高了导引精度。仿真验证了该导引律在不同条件下均能满足过载约束和落角约束。

末制导； 导弹； 多约束； 模糊神经系统； 滑模控制

0 引言

导弹武器因其打击精度高，拦截困难，杀伤力强，越来越成为世界军事研究的热点，导引律则是其中至关重要的一环。一方面，随着高新技术在军事领域的广泛应用，如车辆、舰船、飞机、导弹等武器装备的机动能力有了极大提高；另一方面，现代作战任务的丰富和武器运用的革新使得具有攻击角度约束的制导方法越来越受到各国关注，而目前应用最为广泛的比例导引律已经无法较好地完成这些条件下的导引任务。由于电子技术的发展，导弹导航制导系统的计算能力、控制能力都有了长足进步，这使得将现代控制领域的研究成果应用于导引律设计成为可能。

为了实现终端角度约束，KIM等人[1]首次在导引律的研究中提出攻击角度约束的最优制导律。其后越来越多的学者采用不同的方法，研究各种不同形式的导引律以实现对攻击角度的约束。从19世纪70年代以来，带攻角约束的制导律得到了极大的发展，主要有最优控制导引、偏置比例导引和滑模控制导引。文献[2]通过改进传统的比例导引律，提出了一种基于落角约束的偏置比例导引律，并研究了落角约束对导引律法向过载的影响，通过设计盲区控制方案减小了命中点法向过载，但只考虑了目标静止的情况；文献[3]考虑了目标机动和视场角约束，对偏置项进行了三阶段改进，提出了一种多约束的偏置比例导引律，但该方法存在较大抖振，制导指令过大，抗干扰能力较差；文献[4-5]针对地面固定和慢速移动目标，设计了考虑控制系统延迟和剩余时间的角度约束最优导引律；文献[6]将控制系统视为惯性环节，推导了终端落角约束最优制导律的一般形式。但以上最优导引均要求系统模型准确，且剩余时间的估计对制导性能影响很大。

滑模控制由于其对于非线性系统控制具有良好的鲁棒性和有效性，被广泛应用于落角约束的导引律设计。文献[7]基于滑模理论，考虑自动驾驶仪动态特性，设计了一种有限时间收敛的落角约束导引律，使用饱和函数代替符号函数抑制滑模制导律固有的抖动。但研究表明，随着边界层厚度增加，滑模制导律的鲁棒性将变差，如果减小滑模层厚度又将降低抖振抑制效果[8]。文献[9-10]基于终端滑模控制和有限时间控制理论，提出了一种带攻击角度约束的自适应非奇异终端滑模导引律；文献[11]应用扩张状态观测器对影响制导性能的目标总扰动进行动态补偿，改进了文献[9-10]的方法。以上方法具有良好的鲁棒性，对于干扰和系统不确定也有一定的抗干扰性，但对系统抖动的抑制效果欠佳，且导引律形式非常复杂。

本文考虑攻角约束和过载约束，采用滑模控制方法设计了一种攻击机动目标的非线性导引律，通过引入自适应模糊推理方法，抑制系统可能出现的高频抖动。由于自适应模糊推理方法的自适应能力，使该导引律对于参数摄动和外界干扰具有良好的鲁棒性，并且几乎不存在抖动，最终计算仿真验证了其有效性。

1 问题描述

以纵向平面内的制导律设计问题为例，导弹-目标相对运动关系如图1所示。

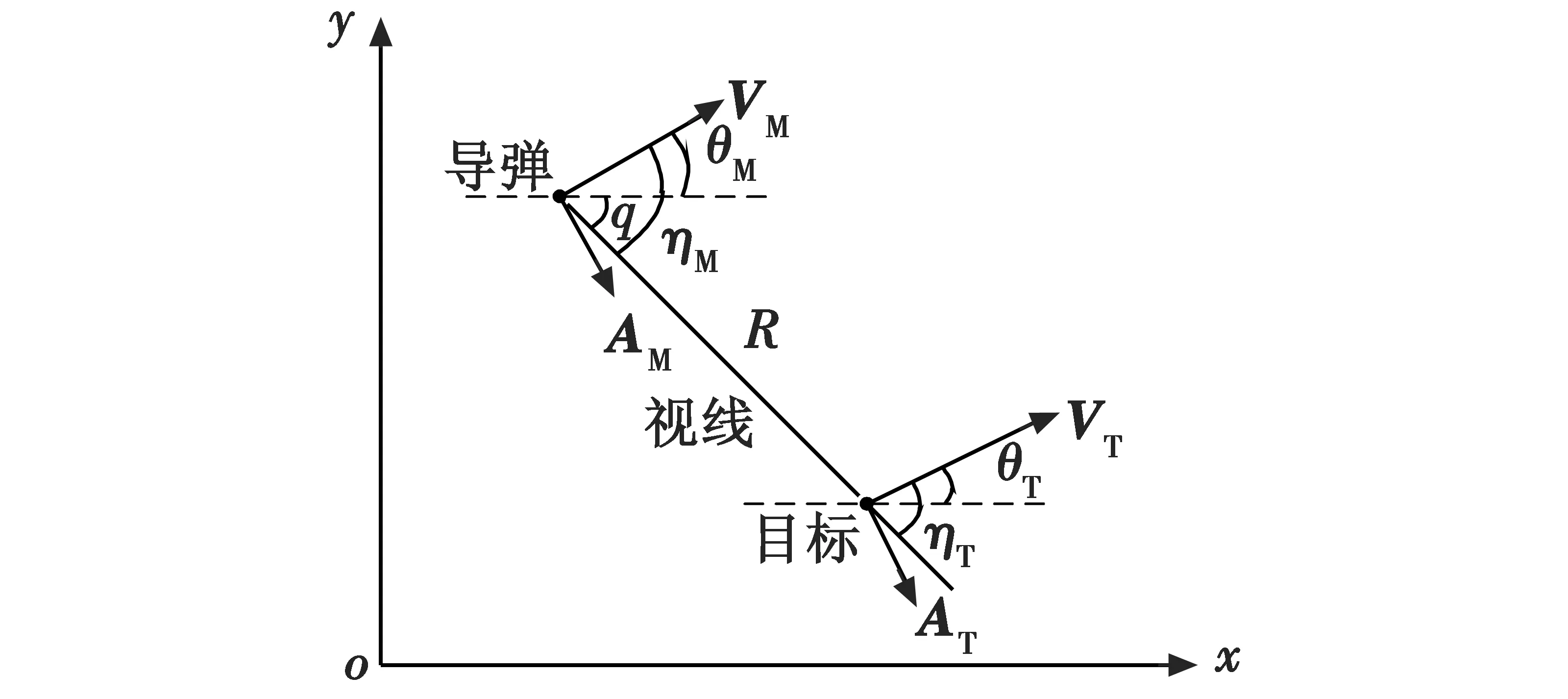
图1 导弹-目标相对运动关系Fig.1 Missile-target engagement geometry

图中：R为弹目相对距离；VM,AM分别为导弹的速度和加速度；VT,AT分别为目标的速度和加速度;q表示视线角；ηM,ηT分别为导弹和目标的视线倾角；θM,θT分别为导弹和目标在纵向平面的航迹角。以上角度均是逆时针为正。

为便于研究，假设：1) 导弹和目标均可视为质点；2) 导弹的速度和航迹角可以通过自身的惯性测量组合准确测量；3) 目标的速度和航迹角可以通过导弹导引系统估计得到；4) 导弹速度大小恒定，且VM>VT；5) 导弹能通过其导引系统测得弹目视线角及其角速度。

在实际的制导过程中，导弹在制导末端发动机推力一般不可控，且制导阶段较短，其控制指令一般也只能改变其速度方向，所以能够作以上假设。

1.1 落角定义

为了便于研究，本文中将落角定义为命中点处导弹速度矢量与目标速度矢量之间的夹角，用θimp表示，方向如图2所示(若目标静止则假设其航迹角为0°)。

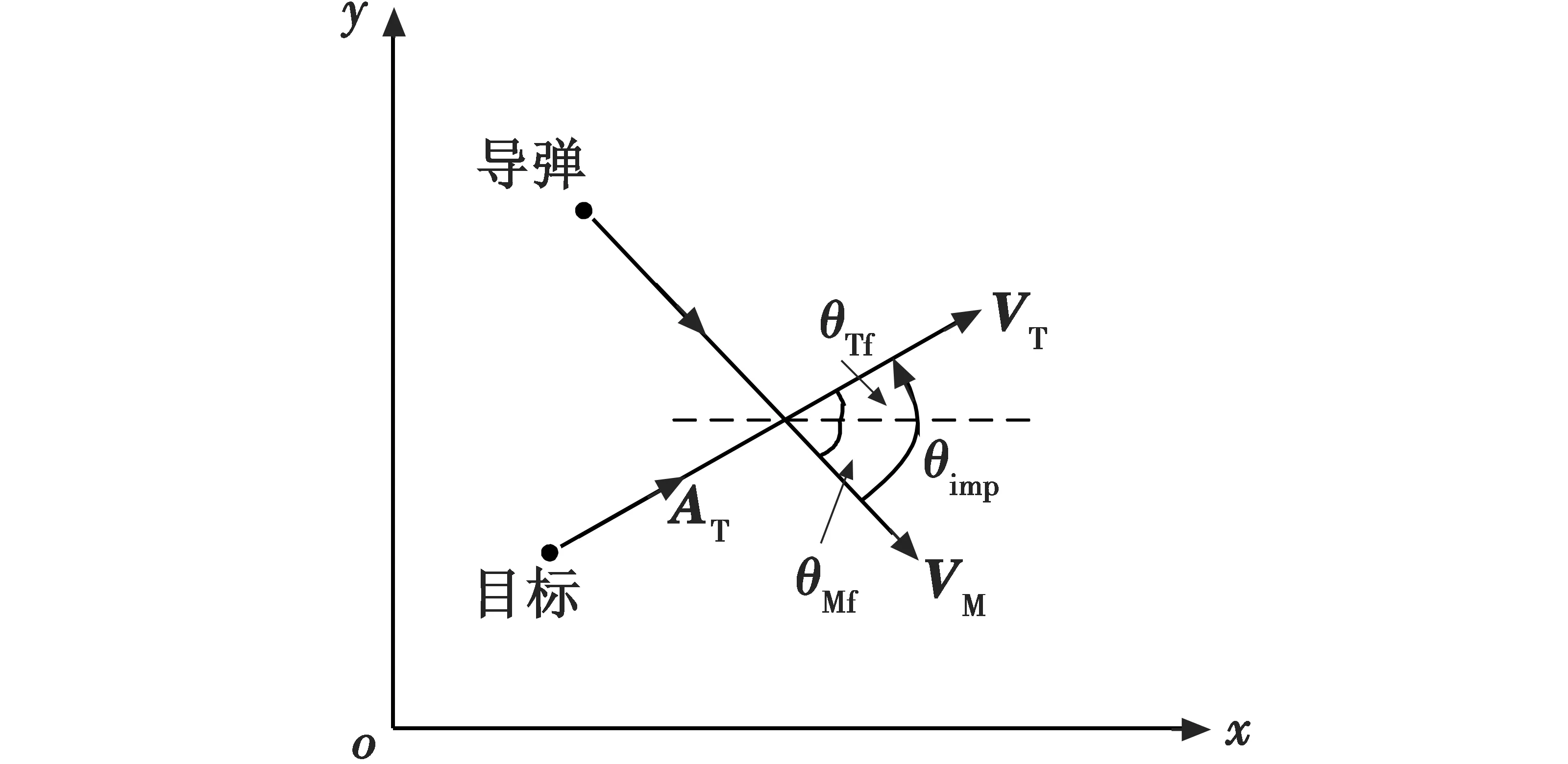
图2 落角定义示意图Fig.2 Definition of impact angle

图中,θTf,θMf分别表示目标和导弹在命中点处的航迹角。由图中几何关系可知

θimp=θTf-θMf。

(1)

1.2 运动方程

根据问题描述及假设，可得到如下微分描述

(2)

(3)

(4)

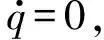
1.3 落角与视线角的关系

VMsinηM=VTsinηT

(5)

且在拦截点处有ηMf=θMf-qf,ηTf=θTf-qf,可推出拦截点处的期望弹目视线角为

(6)

式中,v=VT/VM。以上公式便是拦截点处视线角qf和落角θimp的关系。通过上式，落角约束的问题便能转化为对视线角约束的控制。

2 非线性滑模面设计

在实际中，空气动力误差、测量误差、速度变化和目标机动都极大地影响着导弹制导律的性能。为了提高制导系统的鲁棒性，本文基于模糊推理方法设计了一种鲁棒滑模控制导引律。通过模糊控制方法减小由于滑模控制参数非连续变化引起的系统抖动。

本文所研究的导弹飞行末段处于无动力飞行状态，采用空气舵控制时无法对其切向速度进行控制，故只研究对其法向加速度AM进行控制。

对式(3)求导，并代入式(2)可得

(7)

由上式可知

(8)

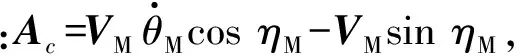
(9)

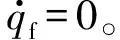
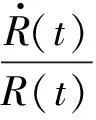
(10)

式中,λ为一个正常量。

为了保证系统状态接近滑模态s=0时具有良好的动态性能，选择以下趋近律函数

(11)

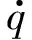
控制的目标是寻找合适的控制变量u使得滑模面和其导数在有限时间内收敛到零。为了分析所选滑模面的稳定性，选取如下李雅普诺夫函数

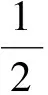
(12)

求导得

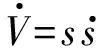
(13)

将式(11)代入式(13)得

(14)

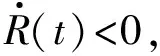
根据式(9)和式(11)，对式(10)求导可得滑模控制导引律形式为

u=AcarccosηM

(15)

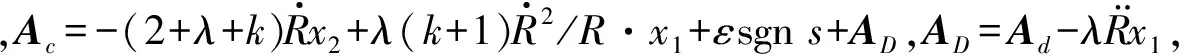
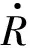
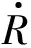
(16)

上式中包含符号函数项εsgns，可能导致系统发生高频抖动。为了削弱可能出现的抖动，下面引入模糊推理方法来解决这个问题。

3 鲁棒导引律设计

虽然上文使用了滑模控制的修正形式来提高导引律的鲁棒性，但其中的高频抖动会降低实际应用中的控制精度。引入模糊推理方法削弱εsgns引起的系统抖振。从式(16)可知，该导引律的性能受符号函数项εsgns影响较大。滑模控制中一般通过引入高增益连续函数或饱和函数替代符号函数减小系统抖动。然而，在针对机动目标时，很难选择合适的参数，既能满足系统鲁棒性的要求，又能减小高频抖动[8]。由于模糊推理具备自主学习能力，故而可以运用到导引律的设计中，达到减小抖动提高系统鲁棒性的目的[13]。

在本文中，运用模糊推理强大的自学习能力，在线修正附加法向加速度指令。

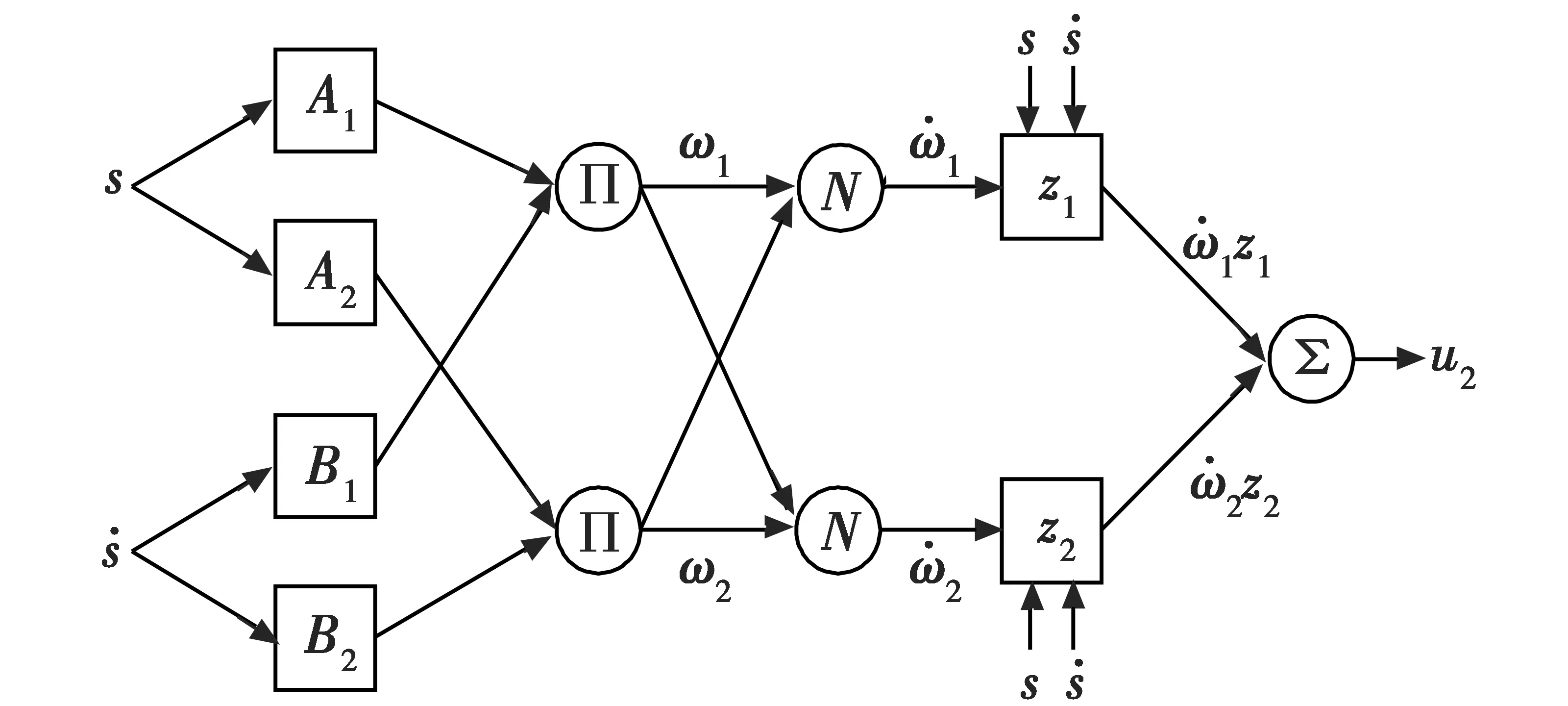
图3 模糊推理结构示意图Fig.3 Schematic diagram of ANFIS

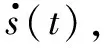
u=u1+u2

(17)

式中，u1=Ac1arccosηM。

3.1 模糊推理方法设计

早在1993年，JANG[14]就提出了基于Takagi-Sugeno模型的模糊推理系。自适应神经模糊推理系统(ANFIS)结构如图3所示，类似于神经网络。考虑神经网络物理意义的不确定性和学习速度的限制，而ANFIS的模糊推理与人的推理方法相似，且具有更快的学习能力，故而选择ANFIS设计导引律。

目前，有很多种ANFIS结构，但使用一阶Sugeno模糊模型的最为常见[15]。

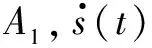
假设输入A(i)和B(i)的隶属度函数是Sugeno模型，形式为

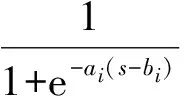
(18)

(19)

式中，{ai,bi}和{ci,di}(i=1,2)是Sugeno函数的特征参数。

由此可知，如果其特征参数改变，该模糊系统的Sugeno函数也将因此改变，相应的隶属度函数也就自适应改变。

根据以上推理系统，能构建以下5层网络结构。其中，同一层的节点函数是相同的函数类，具体如下所述。

1) 输入变量层。

(20)

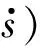
2) 输入语言层。

(21)

各节点的输出分别表示每条规则的适应度。

3) 控制规则层。

(22)

计算相关激励强度与总和之比，对应每一个规则的匹配度。

7) 输出语言层。

(23)

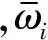
5) 输出变量层。

(24)

本层计算所有上一层到本层输入的加权和，起到解模糊的作用。

这样，就建立了一个基于Sugeno模糊模型的自适应网络。

为了提高导引律的响应速度，通过饱和函数离线训练该模糊推理系统，并代入符号函数，适时更新附加控制指令，其中饱和函数为

sat(s)=s/(s+σ)。

(25)

ANFIS结合了模糊控制和神经网络控制的优势，所以在运用专家经验建立模糊推理规则和自学习自适应能力方面具有良好的性能。

3.2 盲区导引设计

结合上文中的自适应模糊神经网络滑模控制鲁棒导引律，设计了盲区导引策略。考虑导弹的法向过载限制，设计了其法向约束，形式为

(26)

式中，AMmax为导弹的最大法向加速度。在式(26)中通过符号函数AMmaxsgnu限制AM的值，此符号函数不会引入高频抖动，但可以保证该导引律满足过载限制。

在拦截时，当弹目距离小于盲区范围df时，停止导引，定义误差距离为

ed(t)=df-R(t)

(27)

当ed(t)≥0时，停止导引，导弹依靠惯性打击目标；当ed(t)<0时，使用本文推导的自适应模糊滑模导引律(AFSMC)导引导弹打击目标。

3.3 导引律对比

为验证所设计导引律的性能和特性，将其与其他3种导引律，即一般比例导引律(PN)、落角约束的偏置比例导引律(IACBPN)和滑模控制导引律(SMC)进行对比。

1) 一般比例导引律(PN)。

经典的 PN形式简单，可实现性和追踪性能较强，也是目前应用最为广泛的导引律之一。其具体形式可表示为

(28)

2) 落角约束的偏置比例导引律(IACBPN)。

文献[2]在传统的比例导引律的基础上基于落角约束进行推导，得到了一种IACBPN，其简化形式为

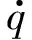
(29)

式中：k为比例导引系数；tgo为剩余时间，这里用tgo=r/VM进行估算。

3) 滑模控制导引律(SMC)。

本文中已经提出了SMC的具体形式见式(16)，并采用饱和函数代替符号函数削弱其抖振。

4 仿真分析

为了验证所设计导引律的性能，首先设计了导弹在不同落角约束条件下的仿真；其次，对比了AFSMC和其他3种导引律在导弹控制系统具有延迟特性以及外界存在较大干扰情况下的导引性能。假设导弹能准确测得θM,q,R(这在主动探测式导引头上是可以实现的)，导弹控制系统具有如式(26)所示的过载限制。

4.1 AFSMC导引律的基本性能

仿真建立的导引坐标系如图1所示，所设计的仿真参数为：导弹初始坐标为(0 m,10 000 m)，速度为900 m/s，方向指向目标，目标初始坐标为(1000 m,0 m)，速度为200 m/s，航迹角为0°，且无机动。AFSMC导引律的参数为：k=1.8，λ=1.5，ε=50，σ=0.01，AMmax=200 m/s2，df=5 m。所设计ANFIS输入的隶属度函数均为钟形函数，本仿真中使用Matlab中的gbellmf，输出为linear，训练次数为100。

在本仿真中，设置导弹的视线角约束分别为(0°,15°,30°,50°,70°)。表1给出了详细的仿真结果，图4给出了相应的仿真曲线。

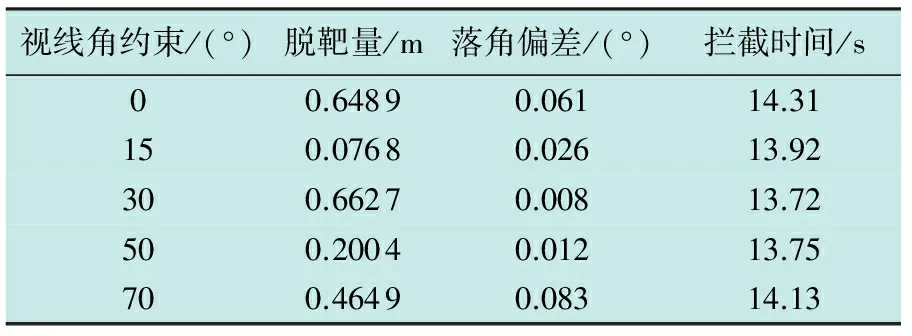
表1 不同落角约束的导引结果

表1中落角偏差表示命中前一时刻的弹目视线角与所约束的视线角之差的绝对值。从表1中可以看出，在AFSMC导引下的导弹能够以较小的脱靶量命中高速运动的非机动目标，同时实现相应的落角约束条件。

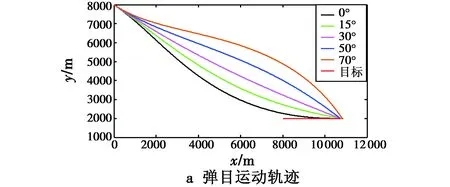
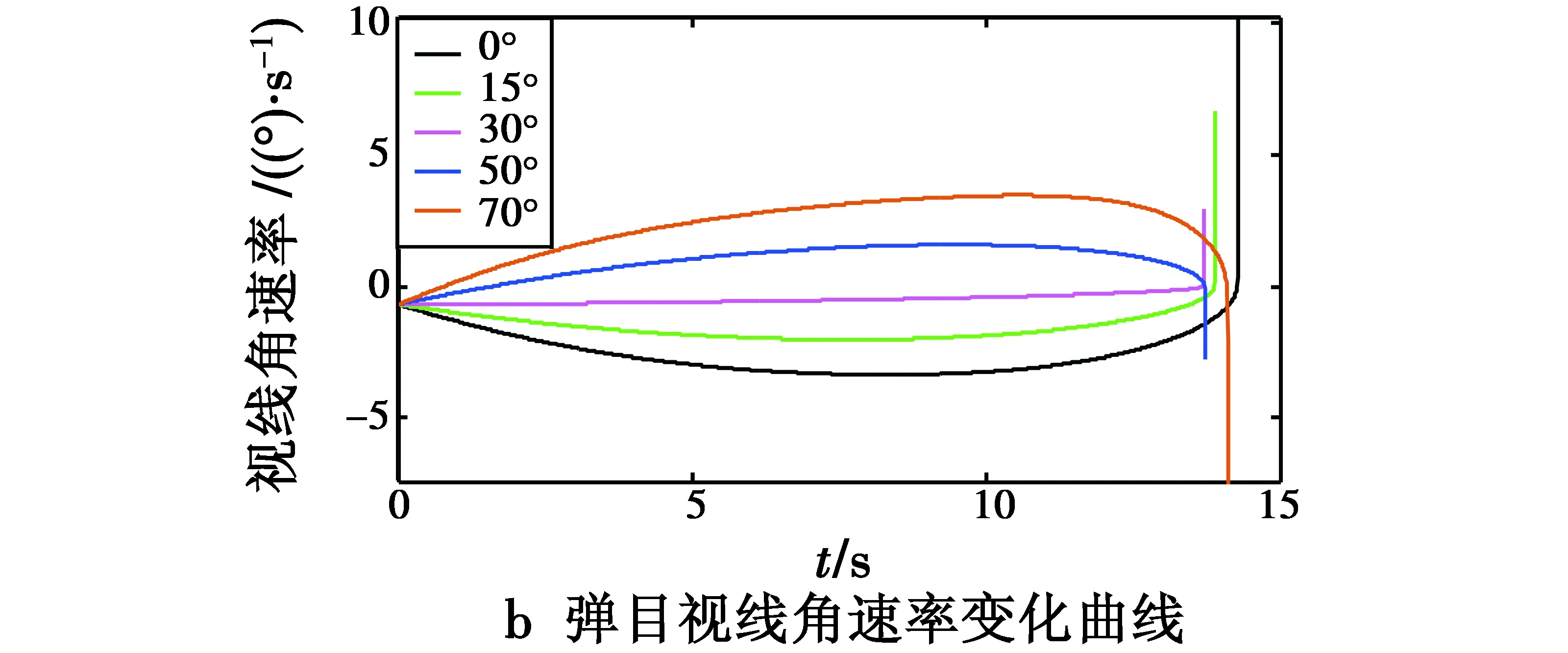
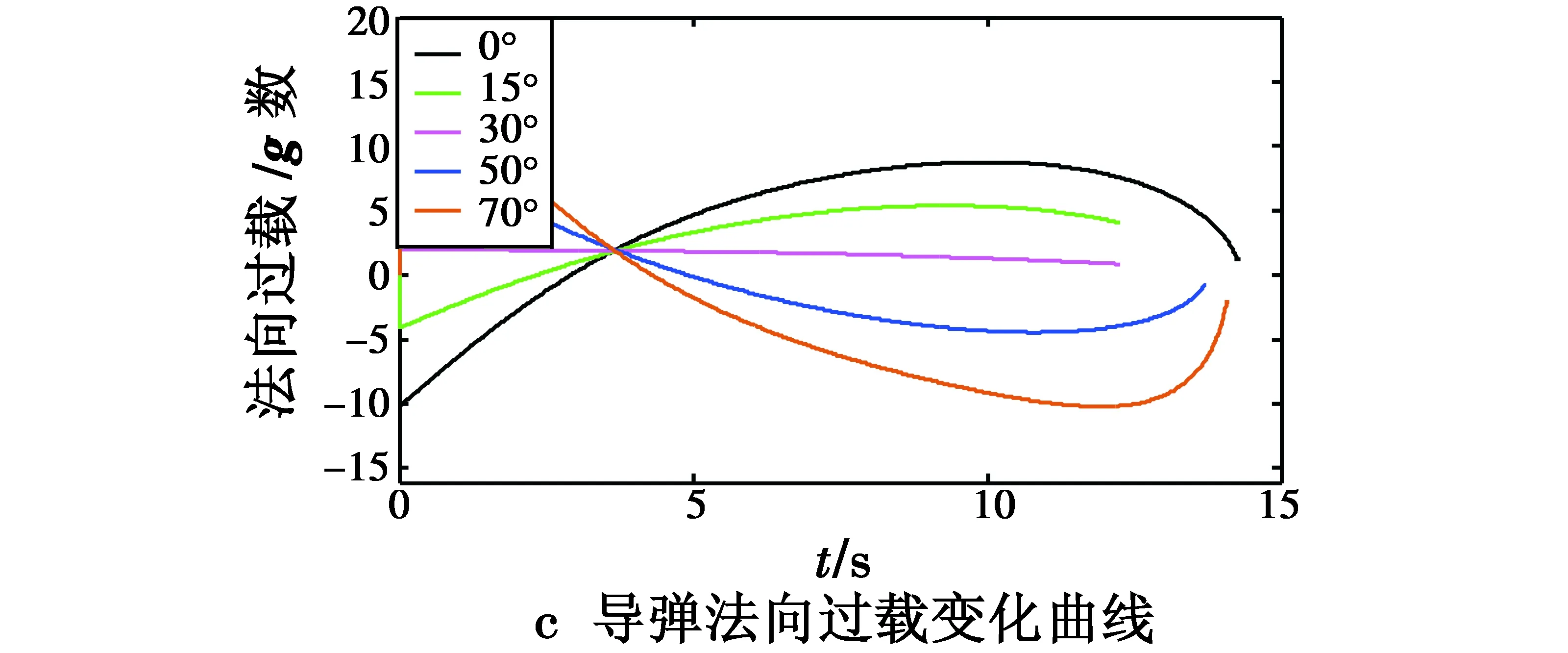
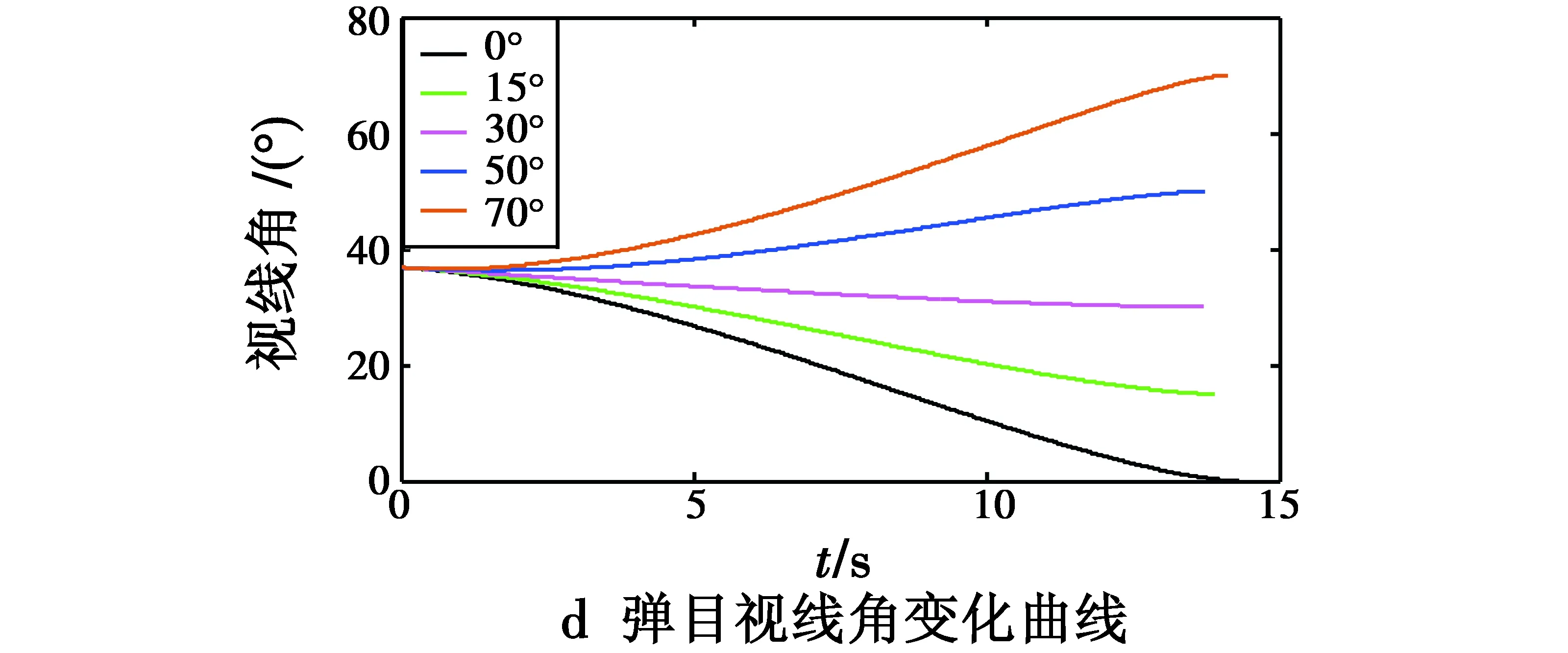
图4 不同落角约束的仿真结果Fig.4 Results of simulation with different impact angles

从图4也可以看出，AFSMC导引下的弹目视线角速率只在最后一刻才发散，保证了较高的落角精度，同时导弹法向过载变化平滑，且均在过载约束范围内。

4.2 多导引律仿真对比

导弹控制系统的动态特性对导引控制的精度影响较大，在本仿真中假设其为一阶惯性环节，表达式为

(30)

式中：u为控制变量；aM为导弹实际加速度；τ为控制时间常数，设τ=0.6。

外界干扰常常使得导弹测量的导引信息具有一定的不确定性，这里假设导引头测得的视线角速率具有零均值，方均根为10-2的高斯白噪声干扰。

坐标系及其他仿真参数设置与4.1节类似，其中,目标在其法向进行幅值为10g的正弦机动，g为重力加速度,视线角约束为80°。

表2给出了仿真的结果，图5给出了相应的仿真曲线。

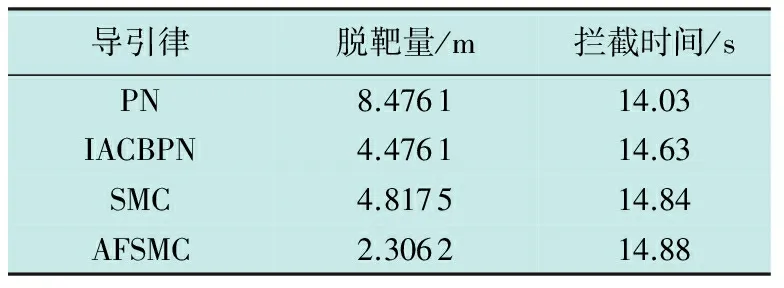
表2 不同导引律的仿真结果

从表2可以看出，在导引头测得的视线角速率存在较大干扰、导弹控制系统具有延迟特性的情况下，由于PN不考虑落角约束，故而拦截时间最短，但脱靶量很大，IACBPN和SMC的制导精度相当，而AFSMC的导引精度最高。

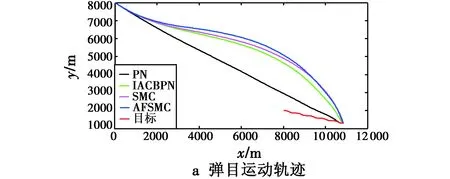
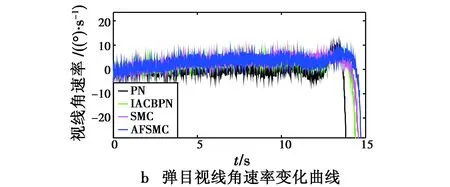
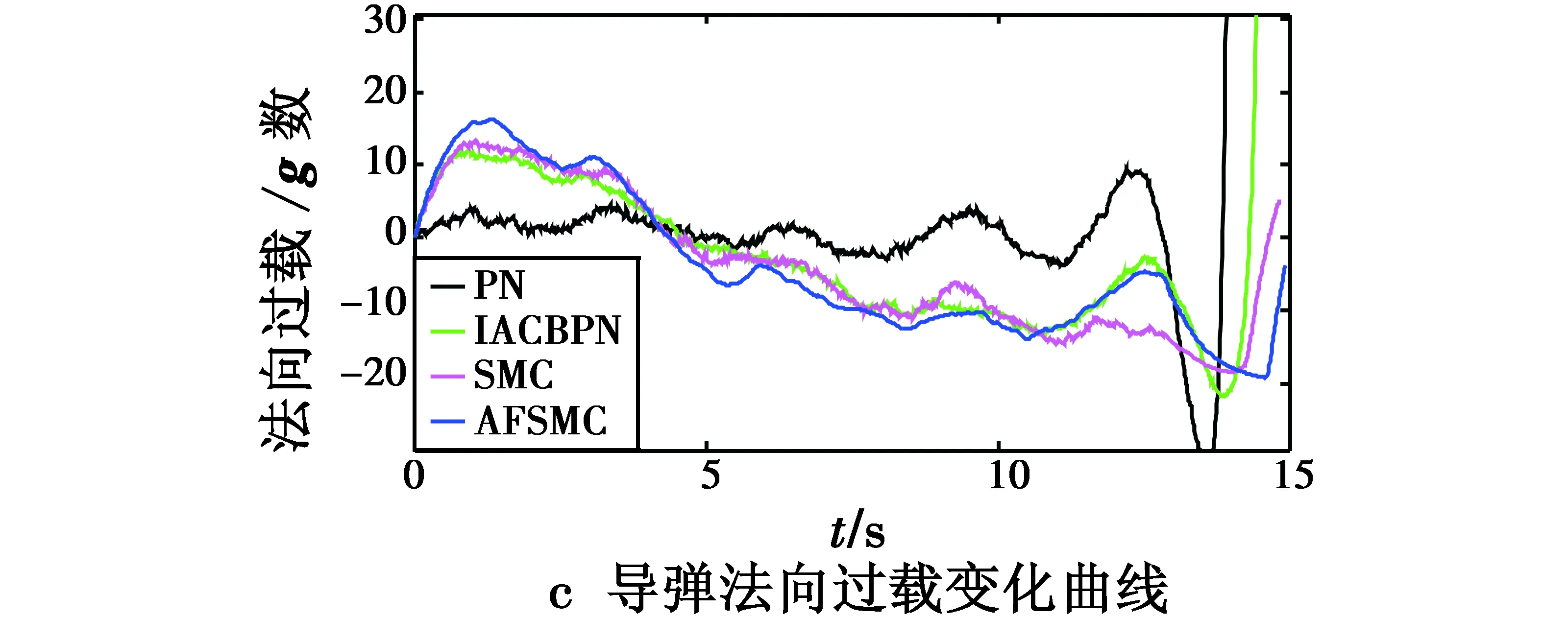
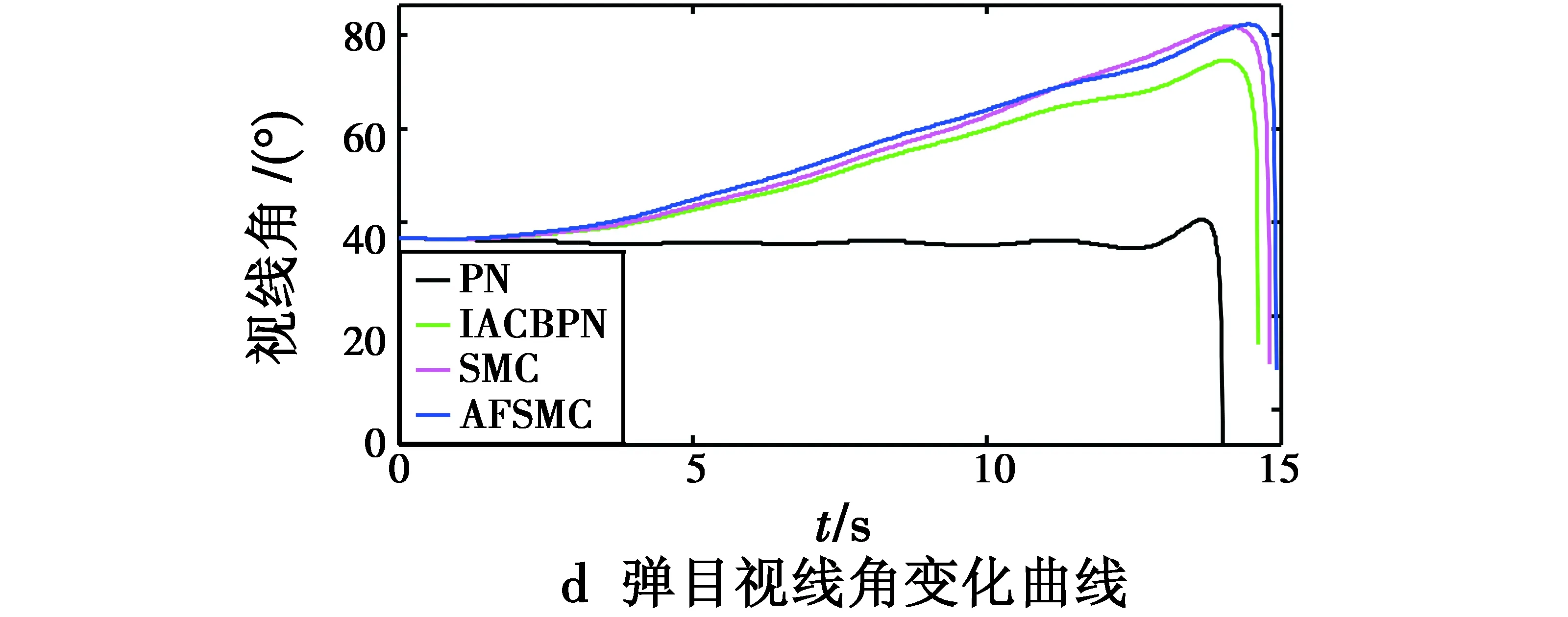
图5 不同导引律的仿真结果Fig.5 Results of simulation with different guidance laws

从图5可以看出，在本仿真条件下，导弹测得的弹目视线角速率具有很大的干扰，而由于导弹控制系统的延迟影响，PN和IACBPN导引下的导弹法向过载在接近目标的过程中呈现发散趋势，超过了过载约束范围；对比可以看出，AFSMC导引下导弹的法向过载相比SMC更为平滑，能够保证控制系统的稳定性能，且其视线角速率在最后时刻才发散，确保了高精度的落角控制。验证了AFSMC良好的自适应性能。

5 结束语

本文针对落角约束的目标拦截问题，结合滑模控制和模糊推理的优势，提出了落角约束的自适应模糊滑模导引律，通过理论分析和仿真验证可以得出以下结论：

1) 采用AFSMC可实现落角约束和过载约束条件下较高精度的导引，能够有效削弱滑模控制中的抖振;

2) 当导弹控制系统存在较大延迟、外界干扰影响导引头测量精度且目标进行大范围机动时，该导引律能够保证良好的控制性能和较高的制导精度;

3) AFSMC的形式简单，计算实时性强，易于工程实践。

在以后的工作中，可以考虑更多的实际问题，如导弹自动驾驶仪动态特性和气动模型等。另外，也可以深入研究针对三维空间的非解耦控制模型的导引律设计。

[1] KIM M,GRIDER K V.Terminal guidance for impact attitude angle constrained flight trajectories[J].IEEE Transactions on Aerospace and Electronic Systems,1973,9(6):852-859.

[2] 高峰,唐胜景,师娇,等.一种基于落角约束的偏置比例导引律[J].北京理工大学学报,2014,34(3):277-282.

[3] 黄诘,张友安,刘永新.一种有撞击角和视场角约束的运动目标的偏置比例导引算法[J].宇航学报,2016,37(2):195-202.

[4] RYOO C K,CHO H,TAHK M J.Optimal guidance laws with terminal impact angle constraint[J].Journal of Guidance,Control and Dynamics,2012,28(4):724-732.

[5] RYOO C K,CHO H,TAHK M J.Time-to-go weighted optimal guidance with impact angle constraints[J].IEEE Transactions on Control Systems Technology,2006,14(3):483-492.

[6] 张友安,黄诘,孙阳平.带有落角约束的一般加权最优制导律[J].航空学报,2014,35(3):848-856.

[7] 孙胜,张华明,周荻.考虑自动驾驶仪动特性的终端角度约束滑模导引律[J].宇航学报,2013,34(1):69-78.

[8] LEE J H,ALLAIRE P E,TAO G,et al.Integral sliding mode control of a magnetically suspended balance beam:analysis,simulation,and experiment[J].IEEE/ASME Tran-saction on Mechanical,2001,6(3):338-346.

[9] 杨锁昌,张宽桥,陈鹏.带攻击角度约束的自适应终端滑模导引律[J].北京航空航天大学学报,2016,42(8):1566-1574.

[10] 熊少锋,王卫红,王森.带攻击角度约束的非奇异快速终端滑模制导律[J].控制理论与应用,2014,31(3):269-278.

[11] 周慧波,宋申民,刘海坤.具有攻击角约束的非奇异终端滑模导引律设计[J].中国惯性技术学报,2014,22(5):607-613.

[12] LI Q C,ZHANG W S,HAN G,et al.Adaptive neuro-fuzzy sliding mode control guidance law with impact angle constraint[J].IET Control Theory & Applications,2015,9(14):2115-2123.

[13] LI H Q,TONG S G.A hybrid adaptive fuzzy control for a class of nonlinear MIMO systems[J].IEEE Transactions on Fuzzy Systems,2003,11(1):24-34.

[14] JANG J-S R.ANFIS:adaptive-network-based fuzzy inference system[J].IEEE Transactions on Systems,Man Cybernetics,1993,23(3):665-685.

[15] WAI R J,HUANG Y C,YANG Y C,et al.Adaptive fuzzy-neural-network velocity sensorless control for robot manipulator position tracking[J].IET Control Theory & Applications,2010,4(6):1079-1093.

Adaptive Fuzzy-Sliding Mode Control Guidance Law with Impact Angle Constraints

WANG Xue-mei1, SHAO Guo-hao-jun1, XU Zhe1, YU Fan2

(1.Rocket Force University of Engineering,Xi’an 710025,China； 2.Institute of Optics and Electronics,Chinese Academy of Sciences,Chengdu 610000,China)

Considering the terminal guidance problem with impact angle constraint and overload constraint,an Adaptive Fuzzy-Sliding Mode Control (AFSMC) guidance law is presented.Its stability is proved by Layapunov stability criterion.The desired impact angle is defined by a desired Line of Sight (LOS) angle,and achieved by design of sliding mode surface.The Adaptive Neuro Fuzzy Inference System (ANFIS) is introduced to reduce the high-frequency chattering of sliding mode control.Since the ANFIS has a powerful self-learning ability,it is applied to adaptive update the additional acceleration command.As a result,the guidance law has good robustness to uncertain chattering and model uncertainty,and the guidance accuracy is improved.Simulation results show that the AFSMC guidance law can meet the requirements of impact angle constraint,overload constraint and miss distance constraint in various scenarios.

terminal guidance; missile; multiple constraints; neuro-fuzzy system; sliding mode control

王雪梅,邵国豪俊,许哲,等.一种落角约束的自适应模糊滑模导引律[J].电光与控制，2017，24(9)：36-41,63.WANG X M,SHAO G H J,XU Z,et al.Adaptive fuzzy-sliding mode control guidance law with impact angle constraints[J].Electronics Optics & Control,2017,24(9):36-41,63.

2016-09-26

2017-07-20

王雪梅(1967 —),女，河北保定人，博士，教授，研究方向为控制科学与工程。

V448.13

A

10.3969/j.issn.1671-637X.2017.09.008