一种基于新的直觉模糊相似度的聚类方法

袁泽华，潘小东

(西南交通大学 数学学院，四川 成都610031)

一种基于新的直觉模糊相似度的聚类方法

袁泽华，潘小东

(西南交通大学 数学学院，四川 成都610031)

针对现有直觉模糊聚类方法中大多数未考虑指标权重，且计算结果为实数的问题，提出了一种基于新直觉模糊相似度的聚类方法。运用直觉模糊熵得到指标权重，构造了一种考虑指标权重的直觉模糊相似度公式，得到直觉模糊相似矩阵，构造了满意度阈值。决策者根据自身满意度偏好选择合适满意度阈值，将直觉模糊相似矩阵转化为实数矩阵，然后利用平方自合成方法得到模糊等价矩阵，选择适当的置信值进行聚类，最后通过实例验证所提方法的有效性和可行性。

直觉模糊相似度；聚类方法；直觉模糊熵；满意度阈值

1965年美国自动控制专家扎德教授首次提出模糊集理论[1]。随着该理论的发展和深入，1986年，保加利亚学者Atanassov提出了直觉模糊集的概念[2]。直觉模糊集是对传统模糊集的一种扩充和发展，增加了新的属性参数：非隶属度函数。相对于传统的模糊集，直觉模糊集在处理不确定性信息时更加的灵活和全面。直觉模糊集理论在模式识别、多属性决策和医疗图像处理等领域得到了广泛的应用。

目前许多学者对基于模糊集提出了很多的聚类方法，比如FCM聚类算法、模糊传递闭包法、编网法等。然而，基于直觉模糊集的聚类方法研究尚处于起步阶段。文献[3]将模糊C-均值聚类算法推广为直觉模糊C-均值聚类,并提出了基于直觉模糊集的聚类方法。该方法虽然考虑了指标权重问题，但其聚类结果为实数。另外，直觉模糊集本身就反映了一定的犹豫程度，其相似度也应该为直觉模糊数的形式；文献[4]针对聚类问题中样品属性值不能直接给出的情况，提出了一种基于集值统计的直觉模糊聚类方法。但该方法直接利用样本集的隶属度进行聚类，而忽视了非隶属度和犹豫度；文献[5]针对已有直觉模糊集聚类方法的局限性，提出了一种基于加权直觉模糊集合的聚类模型。然而现有的直觉模糊聚类方法大多数都是利用直觉模糊集的相似度最终得到一个实数相似度。直觉模糊集本身反映了一定的犹豫程度，其相似度也应该表现出一定的犹豫程度。对此，文献[6]提出了直觉模糊相似度的概念，其值为直觉模糊数，并构建了直觉模糊相似矩阵和直觉模糊等价矩阵及其λ-截矩阵，给出了一种直觉模糊等价矩阵的聚类方法。但其计算量较大且给出的直觉模糊相似度公式不满足定义中的第4条性质。文献[7]提出了基于直觉模糊相似矩阵聚类方法，并直接利用直觉模糊相似矩阵中样本的隶属度对方案直接进行聚类。该方法虽然计算量减小，但未考虑指标权重问题，得到模糊相似矩阵后仅仅采用隶属度作参考进行聚类，造成信息的丢失。

针对现有方法存在的问题，本文定义了任意两个方案之间隶属度距离：非隶属度距离和犹豫度距离。以此为基础构建了一种考虑属性权重的相似度，得到直觉模糊直觉模糊相似矩阵，设计满意度阈值，将直觉模糊相似矩阵转化为实数矩阵，利用平方自合成方法将实数矩阵转化为模糊等价矩阵并进行聚类，解决了现有直觉模糊聚类方法没有考虑指标权重和计算量较大的问题。

1 预备知识

定义1.1[1](模糊集合) 设X是一个给定论域，则X上一个模糊集合A={〈x,uA(x)〉|x∈X}。其中uA(x)表示x属于X的隶属度，uA:X→[0,1]。

定义1.2[2](直觉模糊集) 设X是一个给定论域，X上的一个直觉模糊集A={〈x,uA(x),vA(x)〉|x∈X}。其中uA(x)和vA(x)分别表示为X中的元素x属于X的隶属度和非隶属度，uA:X→[0,1]vA:X→[0,1],且满足条件0≤uA(x)+vA(x)≤1,x∈X，称πA(x)=1-uA(x)-vA(x)为X中元素x属于A的犹豫度。隶属度uA(x)表示对象x属于直觉模糊集A的程度、非隶属度vA(x)表示对象x不属于直觉模糊集A以及犹豫度πA(x)表示对象x对直觉模糊集A中立的程度。例如，假设直觉模糊集A={〈x,0.4,0.5〉|x∈X},即其隶属度uA(x)=0.4，非隶属度vA(X)=0.5,犹豫度πA(x)=0.1，表示对象x属于A的程度为0.4，不属于A的程度为0.5，中立的程度为0.1。X中的元素x属于A的隶属度和非隶属度组成的有序对〈uA(x),vA(x)〉称为直觉模糊数。直觉模糊集A可以看作是X上的全体直觉模糊数组成的集合，记为IFS(X)。

定义1.3[8](模糊度) 设A={〈x,uA(x),vA(x)〉|x∈X}为直觉模糊集,则称：fA(x)=1-|uA(x)-vA(x)|为x在A中的模糊度。

设A={〈x,uA(x),vA(x)〉|x∈X}和B={〈x,uB(x),vB(x)〉|x∈X}为直觉模糊集，则有：

(1)A⊆B当且仅当任意x∈X，有uA(x)≤uB(x)且vA(x)≥vB(x);

(2)A=B当且仅当任意x∈X，有uA(x)=uB(x)且vA(x)=vB(x)。

设C=(cij)m×n是一个m×n矩阵，如果任意cij(i=1,2,...,m,j=1,2,...,n)为直觉模糊数，则称C为直觉模糊矩阵。在模糊集理论中，相似矩阵是一种常见的具有自反性和对称性的矩阵。文献[6]将直觉模糊集理论与相似矩阵结合，提出了直觉模糊相似度和直觉模糊相似矩阵的概念。

定义1.4[6]设σ:Ω2→Θ，Ω为X上所有自觉模糊集的集合，且设Ai∈Ω(i=1,2,3)，若σ(A1,A2)满足以下条件：(1)σ(A1,A2)是直觉模糊数；(2)σ(A1,A2)=〈1,0〉当且仅当A1=A2;(3)σ(A1,A2)=σ(A2,A1);(4)如果A1⊆A2⊆A3，则σ(A1,A3)⊆σ(A1,A2),且σ(A1,A3)⊆σ(A2,A3)。则称σ(A1,A2)为A1和A2的直觉模糊相似度。

定义1.5[4]若直觉模糊矩阵C=(cij)m×n满足以下两个条件：(1)自反性：cii=〈1,0〉,i=1,2,...,m;(2)对称性：cij=cji。则称C为直觉模糊相似矩阵。

2 基于新的直觉模糊相似度的聚类方法

假设一个多属性决策问题有m个可行方案A1,A2,...,Am,n个评价指标I1,I2,...,In，可行方案Ai在评价指标Ij下的属性值为直觉模糊数dij=〈uij,vij〉，可得到直觉模糊决策矩阵D=(dij)m×n。

下面通过构造一种新的直觉模糊相似度进而得到直觉模糊相似矩阵。

定理1 设Ai和Ak为两个直觉模糊集，则

σ(Ai,Ak)=〈αij,βij〉=〈1-d1(Ai,Ak)-d3(Ai,Ak),d2(Ai,Ak)〉

(1)

为Ai和Ak的直觉模糊相似度。

证明: 需要证明公式(1)满足定义4的4个条件。

(1)先证明σ(Ai,Ak)为直觉模糊数。d1(Ai,Ak)≥0,d3(Ai,Ak)≥0；αij=1-d1(Ai,Ak)-d3(Ai-Ak)≤1。

又因为 0≤d1(Ai,Ak)+d2(Ai,Ak)+d3(Ai,Ak)≤1,所以αij=1-d1(Ai,Ak)-d3(Ai,Ak)≥d2(Ai,Ak)≥0。

显然0≤βij=d2(Ai,Ak)≤1，证明了σ(Ai,Ak)为直觉模糊数。

(2)当Ai和Ak相等时，σ(Ai,Ak)=〈1,0〉成立。同理，当σ(Ai,Ak)=〈1,0〉，即αij=1,βij=0，根据所给出的公式可得出Ai和Ak是相等的。

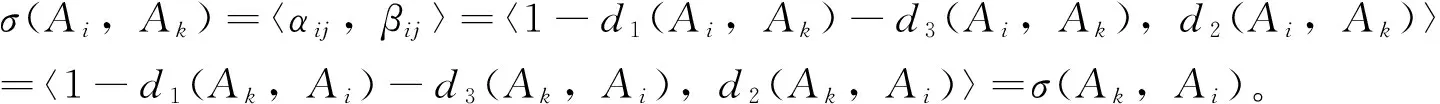
(4)如果A1⊆A2⊆A3，即u1j≤u2j≤u3j,v1j≥v2j≥v3j,j=1,2,...,n则

；

；且 |u1j-u2j|≤|u1j-u3j|,|v1j-v2j|≤|v1j-v3j|，由文献[4]得到|π1j-π2j|≤|π1j-π3j|。所以

即σ(A1,A3)≤σ(A1,A2),同理也可得到σ(A1,A3)≤σ(A2,A3)。

通过上面提出的直觉模糊相似度公式可将直觉模糊决策矩阵转化为直觉模糊相似矩阵D=(dij)m×n，其中cij=σ(Ai,Ak)=〈αij,βij〉为直觉模糊数。

令fij=αij+η(1-αij-βij)，η∈[0，1]为满意度阈值，则可将直觉模糊相似矩阵转化为实数矩阵F=(fij)m×n，然后用平方自合成方法将实数矩阵转化为模糊等价矩阵，再选择合适的置信度λ∈[0，1]对实数矩阵进行聚类。

假如各个指标权重已知的话，直接带入上述公式进行计算，然而在实际中很难直接得到各指标的权重，下面结合直觉模糊熵来计算各个指标的权重。文献[9]提出的直觉模糊熵的公理化定义。

定义2.1[9]∀A,B∈IFS(X),隶属度函数分别为uA(x)和uB(x)，非隶属度函数分别为vA(x)和vB(x)，犹豫度分别为πA(x)和πB(x)。称映射E:IFS(X)→R+为IFS(X)上的熵，如果映射E满足下列条件：

(1)E(A)=0⟺A∈P(X)(P(X)为普通集合的全体)；

(2)E(A)=1⟺∀x∈X,uA(x)=vA(x)=0；

(3)∀x∈X,若πA(x)=πB(x)且fA(x)≤fB(x)，则E(A)≤E(B)。若fA(x)=fB(x)且πA(x)≤πB(x)，则E(A)≤E(B)；

(4)E(A)=E(AC)。

设论域X={x1,x2,...,xn}，A={〈xi,uA(xi),vA(xi)〉|xi∈X}是X上的直觉模糊集，由文献[10]可得到A的模糊熵为：

(2)

特别地，对于直觉模糊数a=〈uA(x),vA(x)〉，其模糊熵为：

(3)

(4)

综上得到新的直觉模糊聚类方法如下：

步骤1：查看指标的权重是否给出。若已经给出，则转步骤3；若未给出，则转步骤2；

步骤2：通过式(4)计算指标权重w=(w1,w2,...,wn)；

步骤3：运用式(1)得到直觉模糊相似矩阵C=(cij)m×n；选择合适的合适的满意度阈值，将直觉模糊相似矩阵C=(cij)m×n转化为实数矩阵F=(fij)m×n,利用平方自合成方法求得模糊等价矩阵。

步骤4：选择合适的置信度λ∈[0，1]对模糊等价矩阵进行聚类。

本文提出的基于直觉模糊相似度的聚类方法与现有的方法对比具有以下两个优点：(1)本文提出的直觉模糊相似度公式的结果仍然是直觉模糊数形式且考虑了指标权重的问题，更加的符合实际情况；(2)本文提出的聚类方法设计了满意度阈值，决策者可根据自身偏好选择合适的满意度阈值，充分考虑隶属度、非隶属度以及犹豫度 3方面的信息。

3 实例分析

为了方便对比，本文引用文献[9]的实例(由于直觉模糊数的定义不同，我们在数据形式上进行了修改，但不影响后面的计算和聚类)。某汽车市场欲对5种不同的车Ai(i=1,2,3,4,5)进行分类，每辆车有6个可供评价的属性指标：燃料消耗量(G1)、摩擦度(G2)、价格(G3)、舒适度(G4)、车身设计(G5)、安全性(G6)。每辆车在各评价属性下的特征信息用直觉模糊数表示，如表1所示。

表1 每辆车在各评价属性下的特征信息

由于指标的权重未知，需计算各指标的权重，根据式(3)和式(4)可得到w1=0.13，w2=0.17，w3=0.17，w4=0.23，w5=0.16，w6=0.14，运用式(1)得到直觉模糊相似矩阵：

选择满意度阈值η=0.5，即满意度中性，得到实数矩阵：

利用自合成方法得到等价矩阵

选取合适的置信水平值λ∈[0,1]，按λ截矩阵t(R)λ进行动态聚类

当0.81<λ≤1，车组Ai(i=1,2,3,4,5)分为5类，即{A1}、{A2}、{A3}、{A4}、{A5};

当0.80<λ≤0.81，车组Ai(i=1,2,3,4,5)分为4类，即{A1}、{A2,A3}、{A4}、{A5};

当0.79<λ≤0.80，车组Ai(i=1,2,3,4,5)分为3类，即{A1,A2,A3}、{A4}、{A5};

当0.74<λ≤0.79，车组Ai(i=1,2,3,4,5)分为2类，即{A1,A2,A3,A4}、{A5};

当0<λ≤0.74，车主Ai(i=1,2,3,4,5)分为1类，即{A1,A2,A3,A4,A5}。

文献[8]提出的聚类方法如下：当0.78<λ≤1，车组分为5类；当0.71<λ≤0.78，车组分为3类，为{A1,A2,A3},{A4},{A5}；当0<λ≤0.71，车组分为1类；没有考虑指标的权重，默认为指标的权重是相同的；利用用户对汽车指标指的隶属度进行聚类而忽视非隶属度和犹豫度，造成用户对汽车评价信息的丢失。从上述结果可以看出，本文提出的新的直觉模糊相似度是有效的。提出的新的聚类方法分类更加详细。可以根据取值不同，分为1到5类。

4 结 语

本文提出的聚类方法分别考虑了指标权重已知和未知两种情况，对于未知的情况运用直觉模糊熵方法得到权重；在得到直觉模糊相似矩阵后，决策者根据自己满意度偏好选择合适的满意度阈值η，并将直觉模糊相似矩阵转化为实数矩阵F，观察实数矩阵是否为等价矩阵，如果不是，则利用平方自合成方法求出实数矩阵的传递闭包t(R),选择合适的置信值λ进行聚类。从实例看出本方法的有效性和可行性。

[1] Zadeh L A.Fuzzy sets[J].Information and Control,1965,8(3):338-353.

[2] Atanassov K T.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1986,20(1):87-96.

[3] 贺正洪,雷英杰.直觉模糊C-均值聚类算法研究[J].控制与决策,2011,26(6):847-850.

[4] 陈晓明,姚泽清.基于集值统计的直觉模糊聚类[J].模糊系统与数学,2011,25(3):100-108.

[5] 吕燕,张仕斌.基于加权直觉模糊集合的聚类模型[J].计算机应用,2012,32(4):1070-1073.

[6] 张洪美,徐泽水,陈琦.直觉模糊集的聚类方法研究[J].控制与决策,2007,22(8):882-888.

[7] Wang Z,Xu Z S,liu S S.A netting clustering analysis method under intuitionistic fuzzy environment[J].Applied Soft Computing,2011,11(8):5558-5564.

[8] 吕印超,郭嗣琮.直觉模糊集的熵及其一般形式[J].计算机工程与应用,2011,47(28):52-55.

[9] 吴涛,白礼虎,刘二宝.直觉模糊集新的熵公式及应用[J].计算机工与应用,2013,49(23):48-51.

[10] 沈小雪,郭嗣琮.新的直觉模糊熵公式及其应用[J].计算机工程与应用,2013,49(23):28-31.

Clustering Method Based on New Intuitionistic Fuzzy Similarity Degree

YUAN Zhehua, PAN Xiaodong

(Xinan Jiaotong Univesity, Chengdu 610031, China)

Aiming at the problem, which most of the existing intuitionistic fuzzy clustering methods do not take the weight of the index into account and the calculation result is real number, a clustering method based on the new intuitionistic fuzzy similarity degree is proposed. By using the intuitionistic fuzzy entropy, the index weight is obtained, and an intuitionistic fuzzy similarity degree formula for attribute weight is constructed as well as an approach is developed to construct an intuitionistic fuzzy similarity matrix. A satisfaction threshold is designed and the decision maker selects the appropriate satisfaction threshold according to their own preference, and transforms the intuitionistic fuzzy similarity matrix into real matrix, then, the fuzzy equivalence matrix is obtained by using the square self synthesis method, selects the appropriate confidence value to cluster. Finally, an example shows the validity and feasibility of this method.

intuitionistic fuzzy similarity degree; cluster method; intuitionistic fuzzy entropy; satisfaction threshold

10.3969/j.issn.1674-5403.2017.04.019

TP18

A

1674-5403(2017)04-0085-05

2017-07-20

袁泽华(1993-),男,江西九江人,在读硕士研究生,主要从事模糊决策和数据挖掘的研究.