基于逾渗理论的非晶合金屈服行为研究∗
2018-01-11平志海钟鸣龙志林
平志海 钟鸣 龙志林
(湘潭大学土木工程与力学学院,湘潭 411105)
基于逾渗理论的非晶合金屈服行为研究∗
平志海 钟鸣 龙志林†
(湘潭大学土木工程与力学学院,湘潭 411105)
非晶合金,逾渗理论,剪切失稳,逾渗阈值
1 引 言
非晶的结构和很多性质遗传于过冷液体,其内部原子排列长程无序、短程有序,是复杂的多体相互作用体系,非晶合金是合金液态相在一定冷却速率下被冻结为非晶态(玻璃态)而形成,因此可以把非晶合金看作是“冻结的液体”[1].这类兼具玻璃与金属双重特性的新材料展现出了优异的力学、物理和化学性质,例如高强度、耐腐蚀和热磁性等[2,3],但大部分非晶合金主要缺陷在于其室温下宏观塑性较差.非晶合金的塑性变形是由于其内部一系列原子扩散和自由体积变化或局部“流动单元”的演变和自组织行为引起[4,5],一些学者认为剪切带的失稳是自由体积和热耦合软化共同作用的结果[6−8],而剪切带的形成实质上是非晶合金塑性流动局部化的结果.为描述非晶塑性流变过程,Spaepen[9]提出了以单原子跃迁为基础的“自由体积(free volume)”模型,Argon[10]提出了以原子团簇(atomic cluster,AC)协同剪切运动为基础的“剪切转变区”(shear transformation zone,STZ)模型.基于自由体积理论,Wang等[11]认为非晶合金剪切带失稳存在临界约化自由体积浓度xC.那么,相对应的非晶合金剪切带失稳时的临界STZs的浓度到底是多少呢?STZ是原子流动时产生的一种动态缺陷,不能从某确定时刻的非晶固体原子图像上事先确定SZT.另外,其定义的是包含一定数量的易于发生塑性变形且拥有剩余自由体积的AC的STZ,如果知道在非晶合金失稳时这些AC临界浓度,则可从另外一个侧面揭示STZ与塑性变形的内在关联.
对一个阻塞(jamming)系统(如非晶合金、颗粒、泡沫等无序体系属于阻塞系统),Liu和Nagel[12]提出温度、应力和密度都能够使之发生阻塞-流动转变.对于非晶合金这类阻塞系统,逾渗理论是一种较好的处理方法[13].逾渗理论(percolation theory)是由Boardbent和Hammersley[14]在1956年提出的,最初逾渗模型被用于描述流体在随机多孔无序介质中的随机扩展和流动.基于逾渗理论并结合橡胶颗粒填充尼龙复合体系的增韧性研究,Wu[15]提出了脆韧转变(brittleductile transition,BDT)理论;李强等[16]在研究非极性PP/EPDM(聚丙烯/三元乙丙橡胶)共混体系时对BDT理论进行了改进和完善,使其能够适用于分析聚合共混物的韧脆转变行为.受改进后的BDT理论启发,本文将逾渗理论应用到非晶合金的屈服行为研究,建立了非晶合金在剪切失稳或屈服时STZ中AC临界浓度的逾渗模型,计算了该浓度的阈值和这些AC的尺寸大小,并得到了一些有意义的结论.
2 理论分析与模型建立
2.1 “自由体积”理论和“STZ”理论
“自由体积”理论认为局部的一系列单个原子的跃迁是非晶合金塑性变形的根源.Spaepen[9]将自由体积vf和流变或应变速率˙γ有效地联系在一起,得到

式中f是Debye频率或原子振动频率;∆f是一个体积比例分数,均匀变形时,∆f∼1;k是Boltzmann常数;T是温度;τ是切应力;va是原子体积;v∗是原子硬球模型体积,满足va=1.25v∗;∆Gm是单个原子跃迁的能量势垒.分析表明,非晶合金的屈服是由于局部自由体积浓度的持续增加导致非晶合金软化.由于实际的自由体积难以测量,于是引入约化自由体积分数x,其定义为x=vf/αv∗(α是对自由体积点重复计算的几何修正因子,一般取值在0.5—1之间).借用引入的约化自由体积x,发现其与黏滞系数η有如下关系:

由(2)式可知,当x持续增加,黏滞系数η逐渐减小,原子的流动性增强,最终导致非晶合金屈服变形.
STZ模型[10]从原子或分子水平上将“自由体积”理论进行拓展和延伸,弥补了自由体积模型不能准确描述低温状态下非晶合金塑性流动过程的不足.STZ模型认为,非晶合金塑性流动是非晶合金中的原子团簇或集团等基本流动单元的时空演化,不是单原子的跃迁或自由体积的变化.总之,无论是自由体积模型还是STZ模型,虽然两者在适用范围上有所不同,但这两种模型均能很好地解释非晶合金的一些屈服行为,如常温下的局域变形与软化、高温下的均匀变形等.
2.2 STZ的逾渗模型
如前所述,对于非晶合金失稳,自由体积的增加有一个临界值(∼2.4%).对应于STZ区,如图1(a)所示,在一个STZ区域内,包含着一定数量的AC,这些AC是富含自由体积的,在外界条件作用下,每个AC会在自己的小范围内发生较大的流动现象.如图1(b),当这些ACs达到一个临界值时,在STZ内会形成一个贯穿整个区域的主连通团,从而导致单个STZ发生屈服,而当多个STZ发生屈服时就会演化为宏观尺度的剪切带.

图1 非晶合金中含有不同大小AC的STZ示意图 (a)AC数量未达到临界值;(b)AC数量达到临界值并形成逾渗连通集团Fig.1.The STZ containing atomic clusters of different sizes in amorphous alloys:(a)The schematic graph of the STZ with the number of ACs not reaching the critical value;(b)the schematic graph of the STZ with the number of ACs reaching a critical value and forming a percolation connected group.

图2 单个AC的等效及屈服 (a)包含原子和自由体积的单个AC;(b)等效自由体积球和应力体积球;(c)AC内原子在τ作用下的流动和应力体积球的屈服Fig.2.Equivalence and yielding of a single AC:(a)The simple AC containing atoms and free volume;(b)the stress volume sphere involving the equivalent free volume sphere;(c)the flowing of atoms in the AC and the yielding of the stress volume sphere under shear stress.
在图2(a)中是单个AC,在这里,我们定义的AC是包含一定数量的原子和自由体积的一个空间区域,即图2中虚线所包围的区域.如图2(b),根据BDT理论的思想,我们将AC中的自由体积等效为一个球体,以这个球为中心,在一定厚度内形成一个应力体积球.图2(c)是当剪应力τ达到非晶合金临界剪应力τC时,AC中的原子的流动,对应着应力体积球的屈服.
图3是对应力体积球的模型简化示意图,d是等效自由体积球的直径,S是应力体积球的直径,TC是临界应力体积球间的厚度.

图3 等效应力体积球示意图Fig.3.The schematic diagram of the equivalent stress volume sphere.
依据Wu[15]的观点,当非晶合金发生韧脆转变时,临界应力体积球间的厚度TC和自由体积球直径d有如下关系:

其中θf是自由体积球的体积分数,它不同于约化自由体积分数.x的表达式为

(4)式中的n是单个AC中所可能包含的原子个数;是这些原子的平均直径,其中非晶合金的平均原子半径可由公式[17]得到,Ai是非晶合金成分中原子半径为ri的原子所占的体积分数.自由体积球的体积分数θf应为

将(4)式代入到(5)式中,就会得到θf与约化自由体积分数x的关系:

由自由体积球的体积分数θf就可以得到应力体积球的体积分数φs[16].
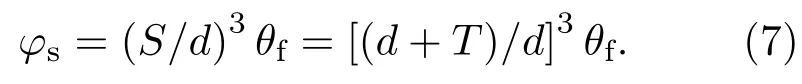
从(6)式可以看出,α是常数,θf只与约化自由体积分数x有关,当x达到临界值时,θf也就达到其临界值θfC,那么φs理论上也会达到其临界值φsC(到后面的计算中会发现φsC与θf无关),而φsC正是我们最终所要获取的.下面以Cu25Zr75为例,计算φsC的大小.
查阅文献[18]知Cu原子直径D1=0.256 nm,Zr原子直径D2=0.32 nm,以Cu-Zr二元合金的成分比例可算得平均原子直径¯D=0.306 nm.根据自由体积理论的观点[9],自由体积v应该满足v6v∗,但v又不能过小,应该大于最小的原子硬球模型体积,即dmin6d6dmax,其中这里我们假设AC在STZ内是随机分布的,而等效的自由体积球在各个AC中是大小相等的单分散分布的,即d的取值是上述范围内的某一固定值.依据Huang等[19]和刘龙飞课题组[20,21]对α值的讨论,取α=0.75较为合适,将xC∼0.024代入(6)式,再代入(3)和(7)式得到了临界塑脆转变阈值φsC=0.524.另外,由(4)式可以得到单个AC在临界状态下包含的原子数的范围是33—64.
通过上面的估算,可以认为:对于非晶合金中的STZ,由于其内部拥有一定体积大小(原子数为33—64)的较易发生流动的原子团,在达到了临界浓度(单分散分布时φsC=0.524)时,STZ发生软化,然后连通其他的STZ形成了一个宏观上较大的软化区,体系发生韧脆转变.
显然,在上面的假设中,我们的设想过于理想与简单化,考虑到非晶合金内部原子结构的无序性,d的取值不应该是单分散的固定值,而是多分散的.因此,我们考虑分散程度对φs的影响,特引入一个重要的分散度σ参数.分散度描述的是等效自由体积球的大小情况和自由体积的聚集程度,其大小分布说明在STZ内形成次连通团时有先后、大小之分.
由于可以将自由体积球看作是嵌入非晶合金基体中的第二相[22],故可将此等效为两相聚合共混体系,所以等效自由体积球的直径d(d∈[dmin,dmax])服从对数正态分布[23],对其定义域内任意直径di,其概率密度f(di)可表示为[24]



由(10)式可知,当所有自由体积球直径d均取某一直径di时,分散度σ与自由体积球的直径di和平均自由体积球直径有关系:lnσ=因此我们按如下规则取σ值:当时(小分布),当时(大分布),假设取最大值与最小值时的分散度是相同的,那么就可以依据得到Cu25Zr75二元非晶合金中的平均直径于是就可以得到σ的最小值σ0=1和最大值σmax=1.12,这样,无论di取何值,其直径的分散度均在[1,1.12]内.
[25],可具体知道相邻应力体积球间厚度T与分散度σ的关系:

将(11)式代入(3)式中便得到新的应力体积球的体积分数φ′s的表达式:


在(11)和(13)式中,相邻应力体积球间厚度T和新的体积分数φ′s中均有两个变量:自由体积球的体积分数θf和分散度σ,所以我们主要探讨这两个变量对T和φ′s的影响.
3 结果与讨论
我们在初始约化自由体积浓度[20,21]x0∼0.008和临界失稳的约化自由体积浓度xC∼0.024之间取五组值,在分散度σ∈[1,1.12]之间取七组值,由(11)式计算结果如表1和图4.由表 1和图4可知,应力体积球间厚度T随着自由体积分数θf的增加而减小,T的减小使得相邻的应力体积球间相互作用加强,可能导致应力场相互交迭,引起大量剪切屈服区,出现较多次生逾渗团,非晶合金的塑性变形变大,这说明自由体积浓度影响着非晶合金在变形过程中的塑性强弱[26];当分散度变化时,其值却基本保持不变,说明T值的大小与分散度σ无关.在初始自由体积分数θf=0.6%时,由于自由体积的浓度较低,而等效自由体积球的直径有一定的范围限制,所以应力体积球间厚度的值较大;当约化自由体积的浓度达到临界值2.4%时,自由体积分数也达到其临界值1.76%,此时的临界应力体积球间厚度TC约为0.57 nm.

表1 在不同自由体积分数和不同分散度情况下计算的相邻应力体积球间厚度(T)值Table 1.Calculated T values at different free volume fractions and different dispersities.

图4 自由体积分数θf和分散度σ对T的影响Fig.4.Effects of free volume fraction θfand dispersityσ on T.
分别固定一个变量时,计算θf和σ对φ′s值的影响,由(13)式计算结果如表2、表3、图5和图6所示.从表2、表3、图5和图6可知,当分散度σ=1时,即等效自由体积球直径分布是单分散的,无论自由体积分数为多少,应力体积球体积分数都保持为0.524的恒定值;无论等效自由体积球直径处于小分布范围内还是大分布范围内,当分散度σ值变化,不再是单分散分布时,对于同一σ值,即便自由体积分数θf在不断增加,虽有极其微弱的减小,但整体上却保持恒定.另外,在小分布范围内,即随着σ值增加,的值明显变大,而σ的变大说明STZ内的自由体积呈现无规分布,在外力作用下较易形成次连通团却不会形成逾渗连通团,说明非晶合金的断裂强度愈高,所以逾渗阈值就会变大;在等效应力体积球直径处在大分布范围内,即随着σ值增加的值明显变小,而σ的变大说明自由体积在STZ内偏聚,在外力作用下较易形成逾渗连通团却不会形成较多次连通团,说明非晶合金的断裂强度较低,所以逾渗阈值就会变小,非晶合金也易发生破坏.但是σ=1和σ=1.12都不太科学,由于等效自由体积球直径符合对数正态分布,因此,非晶合金的塑脆转变阈值应在0.524±0.05之间.
表2 在不同自由体积分数和不同分散度情况下计算的Table 2.Calculated values at different free volume fractions and different dispersities

表2 在不同自由体积分数和不同分散度情况下计算的Table 2.Calculated values at different free volume fractions and different dispersities
约化自由体积浓度x/% 0.8 1.2 1.6 2.0 2.4自由体积球分数θf/% 0.6 0.9 1.2 1.5 1.76 φ′s/%σ=1.0 0.524 0.524 0.524 0.524 0.524 σ=1.02 0.549 0.548 0.547 0.546 0.546 σ=1.04 0.578 0.576 0.574 0.572 0.571 σ=1.06 0.609 0.605 0.602 0.600 0.598 σ=1.08 0.643 0.638 0.634 0.631 0.629 σ=1.10 0.681 0.675 0.670 0.665 0.661 σ=1.12 0.722 0.714 0.708 0.704 0.701
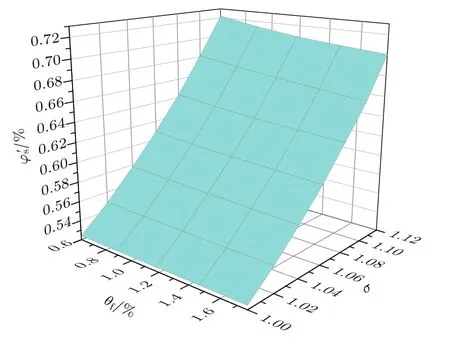
图5 自由体积分数θf和分散度σ对 的影响Fig.5.Effects of free volume fraction θfand dispersity
表3 在不同自由体积分数和不同分散度情况下计算的Table 3.Calculated values at different free volume fractions and different dispersities

表3 在不同自由体积分数和不同分散度情况下计算的Table 3.Calculated values at different free volume fractions and different dispersities
约化自由体积浓度x/% 0.8 1.2 1.6 2.0 2.4自由体积球分数θf/% 0.6 0.9 1.2 1.5 1.76 φ′s/%σ=1.0 0.524 0.524 0.524 0.524 0.524 σ=1.02 0.501 0.503 0.504 0.504 0.504 σ=1.04 0.481 0.483 0.485 0.486 0.487 σ=1.06 0.464 0.468 0.471 0.472 0.473 σ=1.08 0.449 0.453 0.456 0.458 0.459 σ=1.10 0.436 0.440 0.443 0.445 0.446 σ=1.12 0.425 0.429 0.432 0.434 0.435

图6 自由体积分数θf和分散度σ对的影响Fig.6.Effects of free volume fraction θfand dispersity σ on
由以上分析发现,应力体积球间厚度与自由体积分数密切相关,与分散度无关;而逾渗阈值与分散度密切相关,与自由体积分数无关;等效应力体积球间厚度T和逾渗阈值φ′s都是描述非晶合金的塑性变形能力高低的物理量,一定程度上都可以作为非晶合金塑性强弱的判据,T的大小决定着等效应力体积球间厚度的大小,实际上是非晶合金STZ内“增韧粒子”的大小,其对非晶合金力学性能的影响与多孔非晶合金复合材料[27]和内生枝晶相非晶合金材料[28]以及微量添加元素的非晶合金材料[29]目的一样,都是为提高非晶材料的塑性.但这些“增韧粒子”大小有临界值,即当非晶合金塑性能力提高至最优值时,所对应的“增韧粒子”临界体积分数φ′s便是非晶合金韧脆转变的逾渗阈值,而其值大小说明了非晶合金韧脆转变的难易程度,是非晶材料本身的塑性变形能力的体现.且该逾渗模型下得到的韧脆转变的逾渗阈值是非晶合金的特有性质,与临界自由体积浓度[11]和临界应变[30]类似,它不会随初始自由体积浓度和变形过程中自由体积的变化而改变,而与自由体积在非晶合金内部分布特征或聚集状态有关.
4 结 论
本文首次将逾渗理论应用于处理非晶合金屈服时的剪切带形成,基于逾渗阈值处系统特性发生突变的特点,以Cu25Zr75为例,计算分析后得到了以下结论:
1)在STZ内,当内部AC的浓度达到阈值(φsC=0.524±0.05)时,STZ发生屈服,然后STZs会自组织演化为宏观尺度的剪切带,计算的AC中的原子数大约在33—64之间;
2)应力体积球间厚度T随自由体积浓度增加而变小;塑脆转变阈值在小分布范围内随着分散度的增加而变大,在大分布范围内,随着分散度的增加而减小;
3)等效应力体积球间厚度T和逾渗阈值都是描述非晶合金的塑性变形能力高低的物理量,但逾渗阈值是非晶合金的固有特性,不受初始自
参考文献
[1]Wang W H 2013Prog.Phys.33 177(in Chinese)[汪卫华2013物理学进展33 177]
[2]Ding D,Zhang Y Q,Xia L 2015Chin.Phys.Lett.32 106101
[3]Schroers J 2013Phys.Today66 32
[4]Jiang M Q 2014Mater.China33 257(in Chinese)[蒋敏强2014中国材料进展 33 257]
[5]Gao W,Feng S D,Qi L,Zhang S L,Liu R P 2015Chin.Phys.Lett.32 116101
[6]Jiang M Q 2012Acta Mech.Solida Sin.33 227(in Chinese)[蒋敏强2012固体力学学报 33 227]
[7]Wang W H,Yang Y,Nieh T G,Liu C T 2015Intermetallics67 81
[8]Wang Q,Zhang S T,Yang Y,Dong Y D,Liu C T,Lu J 2015Nat.Commun.6 7876
[9]Spaepen F 1977Acta Metall.25 407
[10]Argon A S 1979Acta Mater.27 47
[11]Wang J G,Zhao D Q,Pan M X,Wang W H,Song S X,Nieh T G 2010Scripta Mater.62 477
[12]Liu A J,Nagel S R 1998Nature396 21由体积浓度和变形过程中自由体积演化的影响.
[13]Chen D Z,Shi C Y,An Q,Zeng Q,Mao W L,Greer J R 2015Science349 1306
[14]Broadbent S R,Hammersley J M 1957Math.Proc.Cambridge53 629
[15]Wu S H 1985Polymer26 1855
[16]Li Q,Zheng W G,Qi Z N,Zhu X G,Cai Z L 1992Sci.China:Chem.22 236(in Chinese)[李强,郑文革,漆宗能,朱晓光,蔡忠龙1992中国科学:化学22 236]
[17]Pan D,Inoue A,Sakurai T,Chen M W 2008Proc.Nat.Acad.Sci.USA105 14769
[18]Senkov O N,Miracle D B 2001Mater.Res.Bull.36 2183
[19]Huang R,Suo Z,Prevost J H,Nix W D 2002J.Mech.Phys.Solids50 1011
[20]Liu L F,Hu J,Cai Z P,Li H Q,Guo S B,Zhang G Y 2012Acta Mech.Solida Sin.33 69(in Chinese)[刘龙飞,胡静,蔡志鹏,李会强,郭世伯,张光业 2012固体力学学报33 69]
[21]Hu J 2011M.S.Thesis(Xiangtan:Hunan University of Science and Technology)(in Chinese)[胡静2011硕士学位论文(湘潭:湖南科技大学)]
[22]Arogn A S,Demkowice M J 2008Metall.Mater.Trans.A39 1762
[23]Wu X Z,Zhu X G,Qi Z N 1991Proceedings of the 8th International Conference on Deformation,Yield and Fracture of Polymers London1991 p78
[24]Irani R R,Callis C F 1963Particle Siz:Measurement,Interpretation and Application(New York:Wiley)p40
[25]Liu Z H,Zhu X G,Zhang X D,Qi Z N,Cai Z L,Wang F S 1998Acta Polym.Sin.1 32(in Chinese)[刘浙辉,朱晓光,张学东,漆宗能,蔡忠龙,王佛松1998高分子学报 1 32]
[26]Liu L F,Dai L H,Bai Y L,Ke F J 2008Sci.China:Phys.Mech.Astron.51 1367
[27]Wang B P,Wang L,Xue Y F,Wang Y W,Zhang H F,HuaMeng F U 2016Trans.Nonferrous Met.Soc.China26 3154
[28]Jeon C,Kang M,Kim C P,Kim H S,Lee S 2016Mater.Sci.Eng.A650 102
[29]Yang B,Li X,Luo W,Li Y 2015Acta Metall.Sin.51 465
[30]Wu Y C,Wang B,Hu Y C,Lu Z,Li Y Z,Shang B S,Wang W H,Bai H Y,Guan P F 2017Scripta Mater.134 75
Yield behavior of amorphous alloy based on percolation theory∗
Ping Zhi-HaiZhong Ming Long Zhi-Lin†
(College of Civil Engineering and Mechanics,Xiangtan University,Xiangtan 411105,China)
25 April 2017;revised manuscript
5 June 2017)
According to the microstructure of amorphous crystal,the percolation theory,which is a theoretical approach to dealing with the inhomogeneous physical systems or random fractals,is used to describe the plastic flows of amorphous alloys under shear yielding.In order to understand in depth the critical problems about the shear band initiations in amorphous alloys,a percolation model for shear transformations of these alloys is established by combining with the existing free volume model and shear transformation zone model.Taking the binary amorphous alloy Cu25Zr75for example,the percolation threshold for the shearing instability of the atomic clusters prone to producing plastic flows in the shear transformation zone is calculated when a shear band comes into being.In addition,the size of the abovementioned cluster is also roughly estimated.The calculated results show that the percolation threshold of the shearing instability is similar to the critical reduced free volume value(xC)of∼2.4%for the onset of yielding in amorphous alloy although this threshold is closely related to the dispersity of free volume.The present study may provide a new idea and method of studying the ductile-brittle transition in amorphous alloy.
amorphous alloy,percolation theory,shear instability,percolation threshold
PACS:61.43.Dq,45.10.HjDOI:10.7498/aps.66.186101
*Project supported by the National Natural Science Foundation of China(Grant Nos.51471139,51071134).
†Corresponding author.E-mail:longzl@xtu.edu.cn
(2017年4月25日收到;2017年6月5日收到修改稿)
从非晶合金的微观结构出发,基于处理强无序和具有随机几何结构系统常用的理论方法——逾渗理论来描述非晶合金剪切屈服时的塑性流变.为了更好地理解非晶合金剪切带萌生时的临界问题,结合已有的“自由体积(free volume)模型”和“剪切转变区(shear transformation zone)模型”,建立了非晶合金剪切转变的逾渗模型.以Cu25Zr75二元非晶合金为例,计算了在剪切转变区内易发生塑性流动的原子团簇剪切失稳的逾渗阈值,并粗略估算了这些原子团簇的大小.研究发现,剪切失稳的逾渗阈值与临界约化自由体积浓度(xC∼2.4%)有着相似的特性,不同之处在于其值与自由体积的分散度有着密切联系.研究结果作为非晶合金的韧脆转变问题提供了新思路.
10.7498/aps.66.186101
∗国家自然科学基金(批准号:51471139,51071134)资助的课题.
†通信作者.E-mail:longzl@xtu.edu.cn
