基于响应面的悬浮火箭协同优化设计

张鹏程，杨 军，罗志清，李晓晖

(中国航天科技集团公司四院四十一所，西安 710025)

0 引言

随着海军装备的不断更新，对提升舰艇防御能力的研究就愈加重视。以美、澳联合研制的“Nulka”悬浮火箭型诱饵武器为例，它通过悬浮平飞模拟舰艇运动的方式诱导来袭导弹，且具有快速响应、空中悬浮、全方位覆盖及环境适应能力强的特点[1]，大大提升海军舰艇的防御能力，受到许多国家的广泛关注和研究。

针对传统的飞行器总体设计优化具有研究周期长，研制费用高等缺点，美国等发达国家提出一种多学科设计优化(Multidisciplinary Design Optimization，MDO)。这种优化方法最早由Sobieski提出[2]，其主要优点在于将一个复杂系统分为多个学科进行并行设计优化，学科关系由强耦合变为弱耦合，充分挖掘学科级的设计潜力，通过系统级的优化平衡各学科的设计，最终达到多学科设计的优化目标[3]。目前应用比较广泛的多学科设计优化方法有：并行子空间优化方法(Concurrent Subspace Optimization，CSSO)及基于响应面的CSSO方法，这类方法用于高超声速飞行器的外形尺寸及控制率一体化优化，也被用于求得质量最小化的最优结构布局优化等[4-6]；两级集成系统优化方法(Bi-evel Integrated System Synthesis，BLISS)被应用于亚声速近空间飞行器机翼气动弹性与微机电系统微梁设计等问题[7-8]；协同优化方法(Collaborative Optimization，CO)及基于近似技术的协同优化方法，这类方法应用于船舶设计以及平流层飞艇的总体优化等[9-11]。

提出了基于改进的响应面协同优化方法，简化了目标函数以及系统分析的复杂性，通过拟合系统一致性响应面取消对梯度信息的求解。将该方法以某悬浮火箭为研究对象，研究其总体设计任务，建立多学科分析模型和MDO框架，最终优化并验证得到结果，旨在为将MDO应用到悬浮火箭这类软杀伤武器提供理论基础和方法指导。

1 协同优化方法及其改进

1.1 协同优化方法(CO)

协同优化方法(CO)是一种耦合系统的多级优化过程，协同优化方法将复杂系统分为两层结构：一个系统级和多个学科级。其系统级和学科级数学描述可表示如下。

系统级：

Minf(Z)Z={z1,z2,…，zm}

学科级：

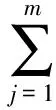
s.t.Gi(X)≤0

Hi(X)=0

协同优化方法(CO)的优化构架如图1，学科级模块之间的连接主要通过系统级的一致性约束。优化过程为将系统级设计变量传递给每个学科级模块进行优化，得到当前最优学科设计变量，将优化后的学科级设计变量传递到系统级生成多学科一致性约束，然后进行系统级优化得到当前最优的系统设计变量，不断迭代从而减小各学科之间的耦合，最终得到满足系统一致性要求的最优设计方案。这种优化构架结构简单，减少学科之间的数据传输，实现了学科级模块的并行自主优化。

对于只有简单双层结构的协同优化方法(CO)，在对实际的复杂系统工程进行设计优化时会带来相应的计算困难：

(1)在实际复杂系统设计中，设计对象的优化目标与设计变量往往不是显式关系，对于过于复杂的(即系统分析或学科分析过于复杂)系统工程会对设计计算带来很大不便，这就使得系统级优化对计算机造成很大负担，无法提高计算效率。

(2)对于系统优化中采用的一致性等式约束是一种理想状态下的优化，没有考虑实际工程设计中不同系统设计变量和学科级设计变量的差别，计算中存在的误差会使得系统优化问题在可行域内无法收敛。

1.2 基于改进的响应面协同优化方法

针对传统协同优化方法(CO)的缺陷，本文提出一种基于改进的响应面协同优化方法，优化流程如图2所示。对于复杂系统设计目标采用均匀设计[12]，选取样本点进行系统分析，运用径向基神经网络技术(Radial Basis Function，RBF)生成系统目标函数响应面。对于系统一致性等式约束，先给定初始中心点和初始置信域，按照中心组合设计原则在初始置信域内选取一系列样本点，将样本点传递到学科级模块优化得到结果，采用二次响应面技术(Response Surface Model，RSM)拟合出系统一致性响应面约束[13]。

具体流程如下：

(1)在可行域内生成设计变量均匀设计表，将系统设计变量进行系统分析，利用RBF生成目标函数响应面fk(Z)。

(2)给定初始中心点Z0，初始置信域Δ0，置信域误差ε1和最优值收敛误差ε2，令k=0。

RBF的优点在于该网络不仅同通常神经网络(Back Propagation，BP)一样具有任意精度的泛函逼近能力，且具有最优泛函逼近特性，同时还具有较快的收敛速度[14]。随着样本点数量逐渐增加，RBF将会越来越逼近真实的映射关系。从图2可看出，该算法含有两个循环，内循环虽然增加了计算量，但也使得系统优化的同时不断提高目标函数精度；外循环使中心点向最优解运动，运动的同时不断缩小置信域，置信域缩小系数决定了算法的优化效率和优化精度，其值越大则搜索面积越大，其结果越精确，但计算效率降低，因此合理的选择置信域缩小系数能有效提高算法的优化效率和精度。

2 悬浮火箭总体多学科优化设计

2.1 悬浮火箭任务设计及优化目标

以某悬浮火箭为例，在接受发射指令后7 s内到达预定60 m左右的悬浮高度，模拟舰艇机动速度约10～20 m/s，其机动距离不下于700 m，悬浮平飞时间不小于27 s，箭体在飞行过程中始终保持在一个平面内，且俯仰角大于75°。

悬浮火箭的飞行轨迹如图3所示分为爬升段、悬浮平飞段、自由落体段。优化目标为在满足发动机总冲一定的情况下提高火箭的悬浮时间。

2.2 悬浮火箭多学科分析模型

悬浮火箭由于飞行速度慢，因此忽略气动因素对箭体的影响，悬浮火箭到达预定高度开始做悬浮平飞运动，为减少火箭各学科的耦合性，将悬浮火箭分为与发动机有关的推进学科、与火箭悬浮控制有关的控制学科以及与飞行轨迹和飞行姿态有关的弹道学科。

对于推进学科，从飞行轨迹可看出发动机为火箭的爬升段和悬浮平飞段提供推力，发动机采用单室双推力发动机，在第一段推力为火箭提供较大推力为其得到较快的速度，第二段推力为火箭悬浮提供推力，随着发动机燃料的不断减小，火箭总质量也在减小。因此，一段逐渐减小的推力不仅能维持火箭的悬浮姿态，也提高了发动机燃料的能量利用率。

发动机的推力曲线可表述为

式中F(t)为发动推力随时间的函数；Fc为第一段推力；Fst为第二段起始推力；Fed为第二段终止推力；t1,t2分别为发动机第一段和第二段的推力工作时间。

对于控制学科，控制回路主要由推力矢量模型和高度控制器组成，推力的矢量控制靠三个线性输出的扰流片呈120°夹角对称分布于喷管外端面，伺服舵机推动扰流片绕转轴转动，通过改变其插入喷管尾流的角度和面积从而实现对推力大小和方向的调节，推力矢量控制选用扰流片为无级调节的连续控制方案，控制器采用传统的PID控制算法[15]。

对于弹道学科，根据推进学科和控制学科的状态输出，根据“瞬时平衡”假设，在准箭体坐标系下建立悬浮火箭六自由度弹道模型[16]，弹道模型主要用于系统分析，生成系统目标函数响应面以及系统状态变量约束响应面。

各个学科的输入输出关系如图4所示。图4中m(t)为火箭质量随时间变化函数；I为发动机总冲；δymax为扰流片在Y方向的最大舵偏；Kp_H为控制器的比例系数；Fyc为推力矢量模型在Y方向的控制力；Tj为火箭进入悬浮高度的时间；Xe为火箭在X方向上的机动距离；Tx为火箭悬浮持续时间。

2.3 悬浮火箭多学科总体设计优化

将悬浮火箭分为推进学科、控制学科及弹道学科，结合基于改进的响应面协同优化构架对悬浮火箭总体设计进行多学科设计优化，其MDO框架如图5所示。

由图5可看出，参与悬浮火箭多学科优化的只有推进学科和控制学科，弹道学科主要用于系统分析，建立系统目标函数和状态变量约束的响应面，系统的优化目标是在发动机总冲不变的条件下使得悬浮时间延长，因此悬浮火箭的系统级的优化问题为

maxfRBF(Fc,Fst,Fed,δymax,Kp_H)

G1(Fc,Fst,Fed,δymax,Kp_H)≤0

G2(Tj,Xe)≤0

H1(I)=0

推进学科的优化问题为

H12(I)=0

控制学科与推进学科具有较强耦合性，因此控制学科的优化问题为

H22(I)=0

3 优化结果与分析

分别用CO算法与基于改进的响应面协同优化算法对悬浮火箭的总体参数进行优化，设计变量的上下限、初始值、初始置信域分量，Δ0及目标函数置信域Δc分量如表1所示。利用Matlab中的Simulink工具箱构建悬浮火箭的六自由度弹道模型，集合iSIGHT软件搭建CO算法与改进算法的优化平台进行悬浮火箭多学科总体设计优化。CO算法在系统级与学科级优化采用序列二次规划法(SQL)进行寻优计算，经过155次迭代最终收敛得到结果。改进算法采用均匀设计方法得到50组系统分析试验样本点，其每次迭代运用中心组合设计增加20组样本点进行系统分析，更新目标函数响应面，置信域缩小系数取0.5，同样运用序列二次规划法进行系统级和学科级的寻优计算，经过14次迭代得到优化结果。

由图6和图7可看出，随着迭代的进行，火箭的悬浮时间逐渐提高，推进学科和控制学科的系统一致性约束也越来越小，最终达到收敛结果。两种优化算法的结果对比如表2所示。

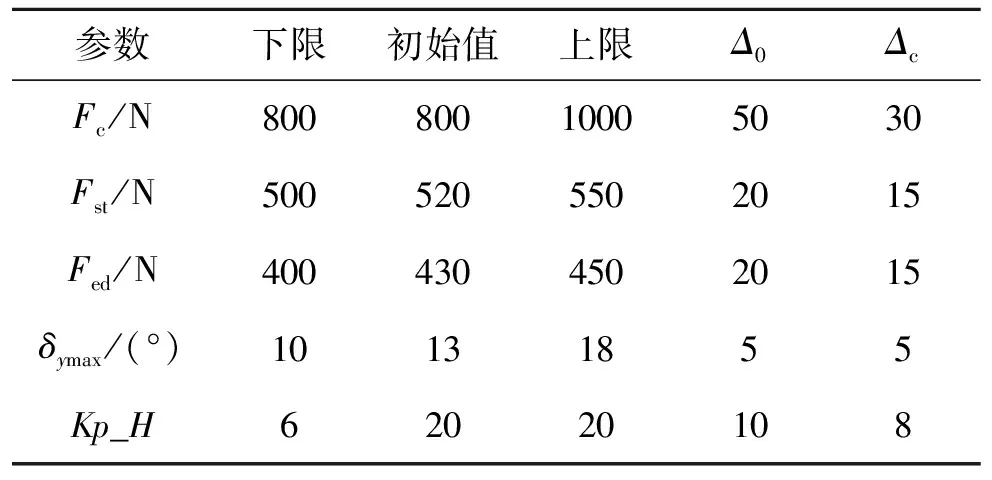
表1 设计变量初始值以及初始置信域分量

参数类型参数优化前CO算法改进算法设计变量Fc/N800841．478855．954Fst/N520512．582508．142Fed/N430424．175409．672δymax/(°)1316．53617．254Kp＿H2017．38416．034状态变量Tj/s6．696．586．06Xe/m702716728Tx/s27．21829．49630．361

由表2可看出，悬浮火箭在总冲一定的情况下，改进算法的优化结果明显优于CO算法，改进算法迭代次数更少，计算效率更高。CO算法因其复杂的系统分析及过度依赖系统一致性的梯度信息增加了计算机的运算负担，而改进算法通过响应面近似技术简化了系统分析求解目标函数的运算量，同时拟合系统一致性约束响应改善了系统优化对梯度信息的求解，提高了系统级的优化效率。

改进算法优化后与优化前相比悬浮时间延长了11.5%，达到了提高悬浮时间的优化目标；机动距离增加了3.7%，这使得悬浮火箭飞行的距离更远，提升了舰艇防御范围；进入悬浮姿态时间提高了9.4%，使得火箭提前进入悬浮姿态，提高了其响应速度，提升了悬浮火箭的总体性能。将优化结果载入弹道模块进行计算，计算结果符合任务设计要求，优化后的发动机推力和主要的弹道参数曲线如图8所示。

4 结论

(1)针对传统协同优化方法的缺陷，提出基于改进的响应面协同优化方法，并通过对悬浮火箭建立学科优化模型和MDO框架进行优化，优化结果表明火箭的悬浮时间得到了提高，验证了悬浮火箭MDO框架的合理性和改进方法的有效性。

(2)通过iSIGHT软件搭建基于改进的响应面协同优化构架，集成Simulink建立悬浮火箭六自由度弹道模型，对悬浮火箭进行多学科总体设计优化，为悬浮火箭MDO研究提供理论基础和工程上的技术指导。

[1] 胡国兵.有源诱饵作战使用 [J].水雷战与舰船防护,2014,22(1):70-73.

[2] Sobieszczanski-Sobieski J.A linear decomposetion method for optimization problems-blueprint for development[R].NASA-TM-83248.1982.

[3] 王振国,陈小前,罗文彩,等.飞行器多学科设计优化理论与应用研究[M].北京:国防工业出版社,2006.

[4] Parashar S,Bloebaum C L.Multi-objective genetic algorithm concurrent subspace optimization (MOGACSSO) for multidisciplinary design [C]//47th AIAA/ASME/ASCE/AH-S/ASC Structures,Structural Dynamics,and Materials Conference.Newport,Rhode Island:May 1-4,2006;AIAA Paper 2006-2047.

[5] 尉建利,王聪,葛颖琛,等.高超声速飞行器操纵性/控制律一体化设计方法[J].固体火箭技术,2015,38(5):601-607,652.

[6] 王毅,姚卫星.桁架结构布局优化的并行子空间方法[J].工程设计学报,2015,22(3):256-261,268.

[7] Sobieszczanski-Sobieski,Sandusky R R.Bilevel integrated system synthesis [R].AIAA 1998-4916.

[8] 许林.飞行器MDO过程及相关技术研究与应用[D].长沙:国防科学技术大学,2009.

[9] Chen S.Zhang F,Khalid M.Evaluation of three decomposition MDO algorithms[C]//23rd International Congress of Aerospace Sciences.Toronto,Canada,2002.

[10] 姚壮乐,陈超核.改进协同优化算法在船舶概念设计中的应用(英文)[J].船舶力学,2014,18(12):1453-1459.

[11] 梁浩全,祝明,姜光泰,等.基于改进CO-RS的平流层飞艇总体设计与优化[J].北京航空航天大学学报,2013,39( 2):239-243.

[12] 王磊.实验设计方法[M].重庆:重庆大学出版社,1997.

[13] Sevant N E.Aerodynamic design of a flying wing using response surface methodology[J].Journal of Aircraft,2000,37(4):562-569.

[14] 张科施.飞机设计的多学科优化方法研究[D].西安:西北工业大学,2006.

[15] 杨军.导弹控制原理[M].北京:国防工业出版社，2010.

[16] 钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2008.