基于MATLAB的轮毂轴承寿命计算
2018-01-11龚晓乾刘学马文伦汪亮
龚晓乾,刘学,马文伦,汪亮
(中国第一汽车股份有限公司技术中心,吉林长春 130011)
基于MATLAB的轮毂轴承寿命计算
龚晓乾,刘学,马文伦,汪亮
(中国第一汽车股份有限公司技术中心,吉林长春 130011)
根据轮毂轴承的不同布置型式,介绍轮毂轴承相关的力学模型及计算方法,以某半浮式驱动桥轮毂轴承为例,论述复杂受力情形时的综合寿命计算;通过MATLAB软件编制程序,指导设计人员进行轮毂轴承的寿命校核及选配。分析计算结果,简述轴荷、轮距、布置形式等因素对寿命的影响。
轮毂轴承;寿命计算;MATLAB
0 引言
轮毂轴承作为承载整车重力并为轮毂转动提供精确引导的关键部件,对保证汽车平稳、安全及可靠行驶至关重要。轮毂轴承的选取主要考虑预期寿命、使用工况、空间结构、安装要求等因素的影响[1],其中预期寿命是实现功能及可靠性的基础。因此,设计人员需掌握轮毂轴承寿命计算,合理选取轴承结构型式。
在上述背景下,作者主要分析了不同布置型式时轮毂轴承(简化为两个单列圆锥滚子轴承)受力状态,并基于MATLAB软件对轮毂轴承的寿命进行计算探讨。
1 车轮力学模型
对于车轮总成,其承受的主要是整车重力及地面施加于车轮的反作用力(径向载荷及侧向载荷)。车辆直行、左转、右转工况时轮荷的分配不同,同时,质心高度、轮距等整车布置参数也影响车轮受力情况。综合各方面因素,车轮(均以左侧为例)受力分析如图1所示。

图1 直行、右转、左转状态(左侧)车轮受力分析示图
图中:W为满载时轴荷,N;H为质心高度,mm;Rw为轮胎滚动半径,mm;Lh为轮距,mm;f为载荷系数;a为侧向加速度,m/s2;Fb为直行时地面作用在轮胎的垂直反力,N;Fbr为右转时地面作用在轮胎的垂直反力,N;Fbl为左转时地面作用在轮胎的垂直反力,N;Far为右转时地面作用在轮胎的侧向反力,N;Fal为左转时地面作用在轮胎的侧向反力,N。
根据图1中车轮力学模型,结合理论力学相关知识,车轮中心面受到地面的反力如下:
(1)车辆直行状态

侧向反力:0
(2)车辆右转状态
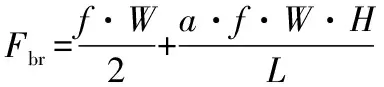
侧向反力:Far=a·Fbr
(3)车辆左转状态
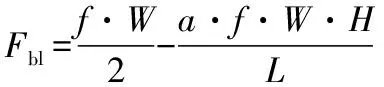
侧向反力:Fal=a·Fbl
2 轮毂轴承力学模型
轮毂轴承既可以应用在驱动轮,又可以应用在从动轮,既可以应用在全浮式车桥,又可以应用在半浮式车桥[4],不同布置型式时轮毂轴承力学模型存在差异。
根据轮毂轴承的使用情况,其力学分析如图2和图3所示。图2为一般轮毂轴承受力状态,轴承主要承受整车重力及地面反力所引起的轴向及径向载荷。图3为某半浮式驱动桥中的轮毂轴承受力情况,在一般轮毂轴承布置型式的基础上增加了驱动齿轮力的输入,需根据实际使用工况将该力分解至轴承,受力情况更为复杂。因而,文中主要以图3所示结构作为计算对象。
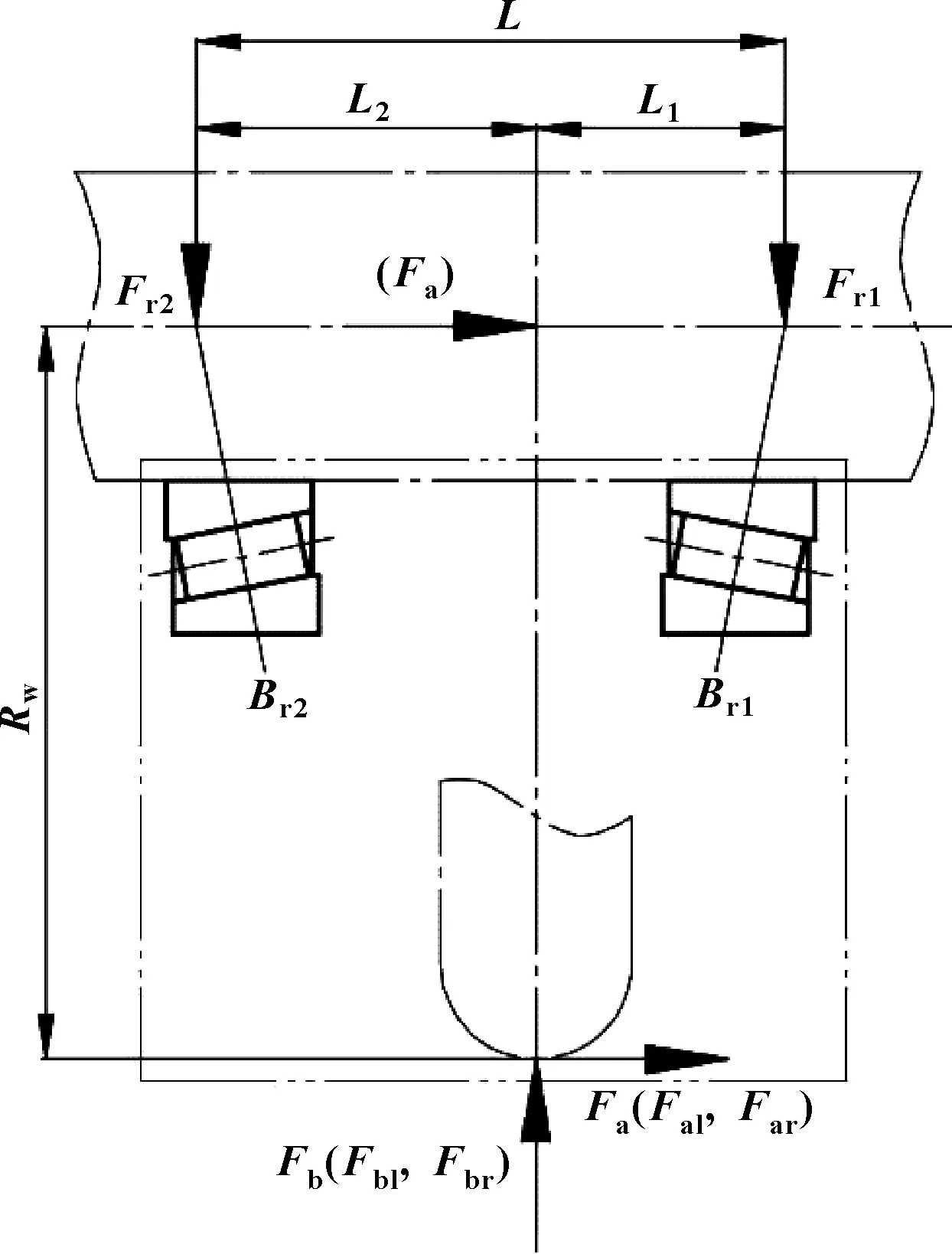
图2 一般轮毂轴承受力分析示图

图3 某半浮式驱动桥轮毂轴承受力分析示图
图中:L为内、外轴承(Br1、Br2)受力点距离,mm;L1、L2分别为内、外轴承距轮胎平面距离,mm;Fr1、Fr2分别为内、外轴承承受的径向载荷,N;Fal、Far分别为左、右转时地面产生的侧向力,N;Fx、Fy、Fz分别为驱动齿轮施加的力。
2.1 轴承径向载荷Fr及轴向载荷Fa分析
2.1.1 径向载荷Fr
径向载荷Fr由图3根据理论力学相关知识计算确定。
2.1.2 派生轴向力Fd
圆锥滚子轴承在承受径向载荷时产生派生的轴向力Fd[2-3]的计算公式为:
2.1.3 外加轴向载荷Fao
在布置上,圆锥滚子轴承组的内外轴承所受外加轴向力可以分为独立和关联两种形式进行讨论,如图4和图5所示。主要差别体现在轴承轴向力的大小及方向判定。
图4结构中外加轴向力(车轮力及驱动力Fz)分别作用在单个轴承上,不传递到另一侧。
图5结构中外加轴向力(车轮力及驱动力Fz的合力)同时作用在两轴承。
(1)当两轴承受力相互独立时,外力产生的轴向力如表1所示。其中Fao、Falo、Faro分别为直行、左转、右转时地面和主动齿轮作用的总轴向力,单位N。
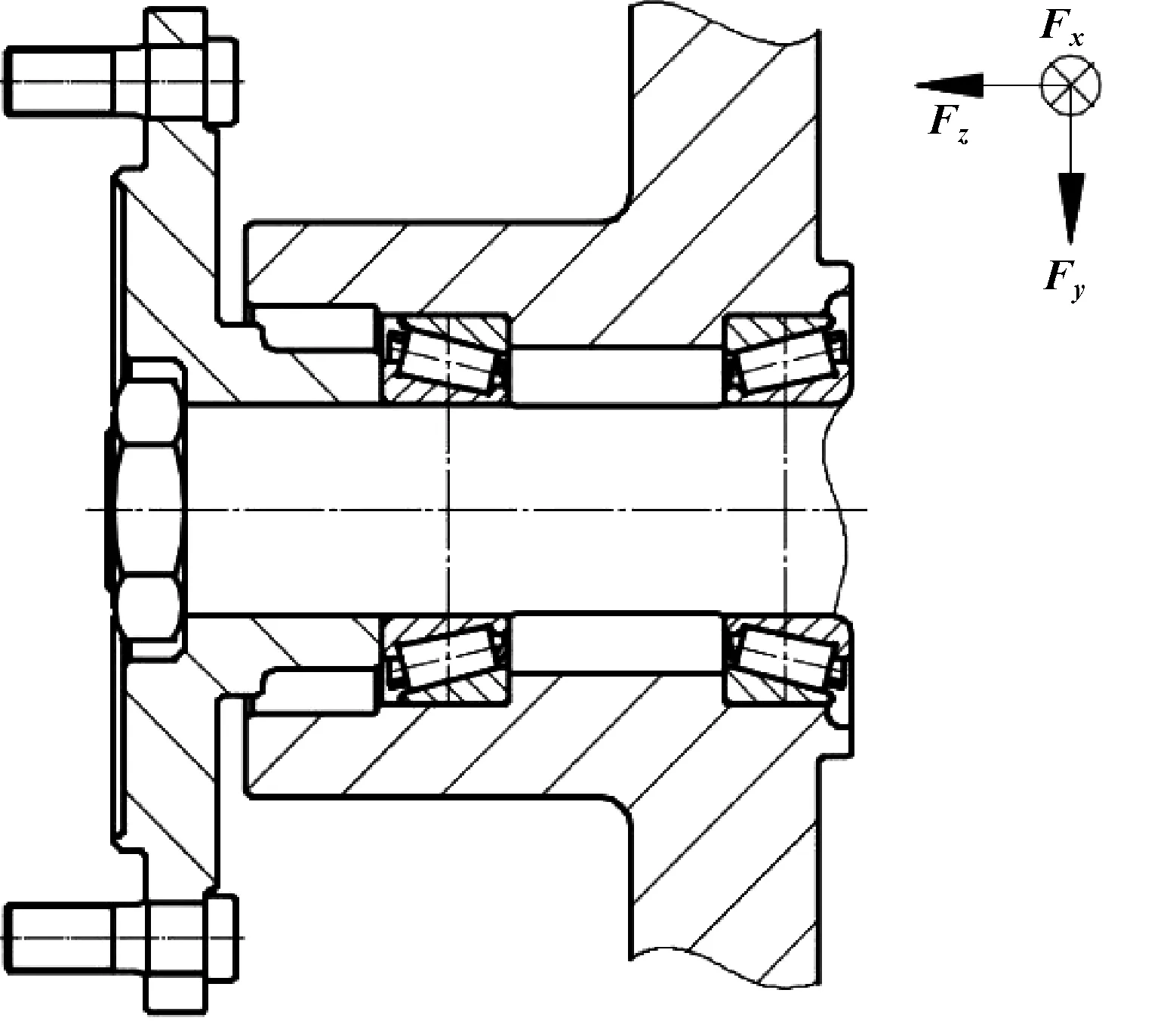
图4 内外轴承外加轴向力相互独立

图5 内外轴承外加轴向力相互影响

表1 两轴承受力独立时外力产生的轴向力
(2)当两轴承受力相互影响时,外力产生的轴向力如表2所示。其中Fao、Falo、Faro分别为直行、左转、右转时地面和主动齿轮作用的总轴向力,单位N。

表2 两轴承受力关联时外力产生的轴向力
2.1.4 轴向载荷Fa
(1)当两轴承受力相互独立时,其轴向载荷主要与作用在单个轴承上的外加轴向力及派生轴向力合力有关。
Fa=|Faa±Fd|
式中:Faa为外加轴向力合力,单位N。
(2)当两轴承受力相影响时,需对各轴承的窜动趋势(“压紧”或“放松”)进行判断,见表3,进而确定轴向力的大小。表中Faa为外加轴向力合力,单位N。

表3 轴承受力相关联轴承轴向载荷判别
2.2 当量动载荷P计算
对于圆锥滚子轴承,同时承受轴向载荷Fa和径向载荷Fr,在寿命计算时需将实际载荷转换为当量动载荷P。
当量动载荷的计算公式为
P=X·Fr+Y·Fa
式中:P为当量动载荷,N;Fr为径向载荷,N;Fa为轴向载荷,N;X为径向动载荷系数;Y为轴向动载荷系数。
3 轮毂轴承寿命计算
滚动轴承的寿命与所受载荷有关,工作载荷大时其接触应力也大,因而寿命越短。为表征不同轴承在某一寿命条件下的承载能力,定义了基本额定动载荷C,即使轴承的基本额定寿命恰好为100万转时轴承所能承受的载荷。但当载荷P不为基本额定动载荷C时,就要根据实际情况去计算所选轴承的预期寿命,以满足使用要求。
3.1 轴承预期寿命
根据每个轴承的当量动载荷P及从轴承手册查得该型号轴承基本额定载荷C,可计算轴承预期寿命。
图6所示为轴承载荷P与基本额定寿命L10之间关系[2],其公式可表示为
式中:L10为基本额定寿命,106r;ε为指数,滚子轴承取10/3,球轴承取3。

图6 轴承的载荷-寿命曲线
3.2 综合行驶里程(寿命)
由于轮毂轴承搭载在车辆上使用,以车辆行驶里程来判断轴承使用寿命更为简便。此外,不同行驶工况(转弯频率、路况、使用环境等)存在不同的冲击系数[5],见表4。因此,考虑诸多影响计算过程中将基本额定寿命转化为综合行驶里程。
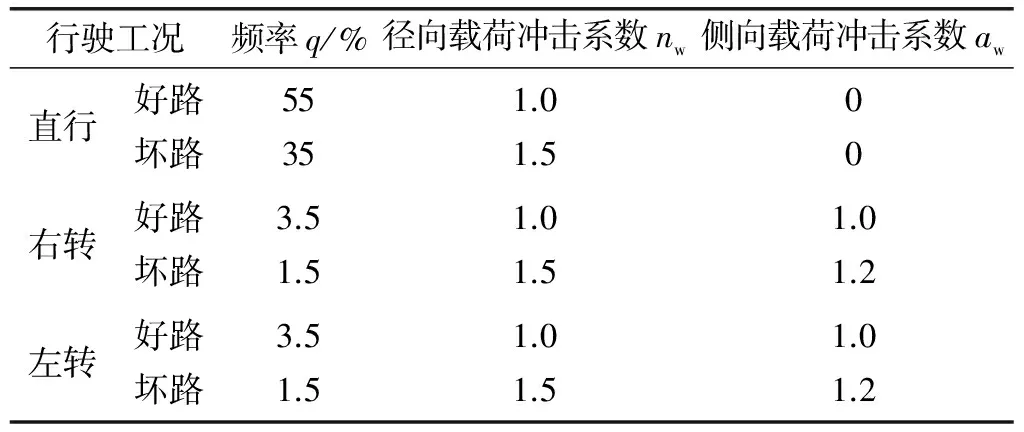
表4 各行驶工况频率及冲击系数经验值
4 基于MATLAB轮毂轴承寿命计算程序
应用MATLAB软件编制计算程序,通过GUI界面实现数据输入及结果输出的可视化[6-7]。
4.1 轮毂轴承寿命计算流程
轮毂轴承寿命计算流程见图7。

图7 轮毂轴承寿命计算流程图
4.2 轮毂轴承寿命计算结果
(1)分别根据轴荷变化及轮距变化计算内外轴承综合寿命,如图8所示。

图8 内外轴承计算结果
轴荷变化比轮距变化对轴承寿命的影响更大,且外侧轴承的寿命对各因素变化更加敏感。
(2)外加轴向力相互独立及相互影响的轴承综合寿命,如图9所示。

图9 独立与关联轴承对比
在相同型号轴承及布置参数情况下,两轴承的外加轴向力是否相互影响对轴承寿命具有较大的影响。
5 结束语
从计算结果可以看出:轮毂轴承在整车中的布置型式(驱动轮与否、半轴结构型式、受力关联与否、轴距等)及使用条件(轴荷等)对其寿命具有重要影响;轴荷变化比轮距变化对轮毂轴承寿命的影响更大,且外侧轴承对变化更为敏感。通过该方法对某车型车轮毂轴承进行相关校核选配,在整车试验及使用周期内使用情况良好。
另外,对车辆其他轴承的寿命计算选配,综合使用寿命的确定也需根据使用部位的具体工况设定相关加权系数。
[1]高秀荣.汽车轮毂轴承结构型式选取及寿命影响因素[J].汽车工程师,2016(6):48-52.
GAO X R.Selection of Vehicle Hub Bearing Structure Type and Life Influence Factors[J].Auto Engineer,2016(6):48-52.
[2]濮良贵,纪名刚.机械设计[M].8版.北京:高等教育出版社,2006:319-320.
[3]彭文生,李志明,黄华梁.机械设计[M].2版.北京:高等教育出版社,2008:419-427.
[4]王望予. 汽车设计[M].4版.北京:机械工业出版社,2004:165-166.
[5]董晓,陈东照,邓四二,等.轿车轮毂轴承疲劳寿命的计算与分析 [J].河南科技大学学报(自然科学版),2014,35(5):19-23.
[6]陈杰.MATLAB宝典[M].4版.北京:电子工业出版社,2013.
[7]王正林,刘明,陈连贵.精通MATLAB[M].3版.北京:电子工业出版社,2013.
TheCalculationofHubBearingLifeBasedonMATLAB
GONG Xiaoqian,LIU Xue, MA Wenlun,WANG Liang
(Research & Development Center, China FAW Corporation Limited,Changchun Jilin 130011, China)
According to the different layouts,the mechanical model and calculation method of hub bearings were introduced. Taking a semi-floating driving axle as an example, the calculation of hub bearing comprehensive life was discussed.Program written by using MATLAB software was used for calculation of hub bearing life and selection.By analyzing the results, the influences of the axle load, track, layout for the life of bearing were briefly described.
Hub bearing;Life calculation;MATLAB
2017-09-30
龚晓乾(1988—),男,工学学士,工程师,主要从事汽车转向系统设计开发工作。E-mail:gxqxiaoqian@163.com。
10.19466/j.cnki.1674-1986.2017.12.004
TH133.3
B
1674-1986(2017)12-014-05
