基于稳定系数法的盾构隧道开挖面失稳概率分析

， ，，

(1.中国科学院 a.武汉岩土力学研究所; b.岩土力学与工程国家重点实验室,武汉 430071； 2.中国科学院大学, 北京 100049)

基于稳定系数法的盾构隧道开挖面失稳概率分析

程红战1a,1b,2，陈健1a,1b,2，胡之锋1a,1b,2，黄珏皓1a,1b,2

(1.中国科学院 a.武汉岩土力学研究所; b.岩土力学与工程国家重点实验室,武汉 430071； 2.中国科学院大学, 北京 100049)

基于B. B. Broms等提出的开挖面稳定系数的概念，结合概率分析方法，考虑了土性参数的空间变异性，将黏土参数不排水抗剪强度看作服从对数正态分布的随机变量，形成了盾构隧道开挖面稳定性概率分析法;并讨论了不排水抗剪强度的变异系数和其均值随深度线性增加的特征对开挖面失稳概率的影响规律。研究结果表明:黏土参数不排水抗剪强度的空间变异性对盾构隧道开挖面稳定性有着重要的影响,参数变异程度越高，开挖面发生失稳破坏的概率也就越大;开挖面失稳概率会随着线性系数的增大而逐渐降低。单一的开挖面稳定系数很难恰当地反映盾构隧道开挖面的稳定性状态，而采用失稳概率的表示方法更为合适。

隧道；开挖面稳定性；稳定系数；空间变异性；概率方法

1 研究背景

随着我国经济的蓬勃发展，城市轨道交通逐渐成为一个衡量城市发展程度的重要指标。盾构法隧道施工以其环境影响小、施工安全性高以及地层适应强等优点，已经成为城市轨道交通建设的重要施工方法[1]。为了平衡盾构隧道开挖面前方的水土压力，施工过程中需要对开挖面提供适当的支护压力，以维持其稳定性。支护压力过小，就会引起地表沉降，支护压力过大则会诱发地表隆起。因此，盾构隧道开挖面稳定性一直是一个非常重要的问题，国内外学者也做了诸多针对性的研究[2-6]，其研究方法包括了极限分析、极限平衡和数值模拟等。但是，目前多数研究成果均是在假设岩土体为均质、各向同性的材料的基础上提出的，未能考虑岩土体参数的空间变异性特征[7]。

最近几年来,关于概率分析方法在隧道开挖面稳定性方面的研究才日益受到关注。国内研究学者李志华等[8]提出了采用可靠度的方法来评价土体参数的变异性对盾构隧道开挖面稳定性的影响程度，对于盾构施工过程也具有一定的参考作用。国外研究中Mollon等[9-10]基于随机响应面的方法重点研究了土性参数内摩擦角、黏聚力的空间变异性对开挖面极限支护压力和失稳模式的影响。Eshraghi等[11]与实际工程相结合，研究了多个土性参数的不确定性对土压平衡盾构施工断面开挖面极限支护压力的影响，并与现场监测数据相比较得出，采用概率分析方法得到的结果更加可靠。以上研究成果在一定程度上提高了土性参数的空间变异性对盾构隧道开挖面稳定性影响的认识，但是，上述研究更多的停留在定性-半定量的层面，很难直接应用于工程设计当中。

本文基于Broms等[2]提出的开挖面稳定系数的概念，结合概率分析方法，考虑了土性参数的空间变异性，将黏土参数不排水抗剪强度看作服从对数正态分布的随机变量，形成了盾构隧道开挖面稳定性概率分析法。重点分析不排水抗剪强度的变异系数和其均值随深度线性增加的特征对开挖面失稳概率的影响，形成了一定的规律性的认识，可为工程设计提供参考。

2 土体参数的空间变异性特征

物质组成的差异和复杂的沉积过程，导致土体表现出非均质性的特征。岩土体中不同点之间的物理力学性质参数也呈现出一定的差异性。蒋水华[12]统计了不同地区不排水抗剪强度cu的变异系数COV(标准差与均值的比值)的取值情况(表1)。可以看出，不同地区土层cu的统计结果均表明具有一定程度的变异性，而且不同地区之间的差异性也比较明显。众所周知，cu并非土体的固有性质参数，其大小还与土体所处的应力状态有关，所处应力水平越高，土体的不排水抗剪强度也越大。Lumb[13]根据土体参数均值和标准差随深度的变化关系，将土体参数空间变异性划分为3种类型，如图1所示。类型1为参数均值和标准差都不随深度变化；类型2为参数均值随深度线性增加，而标准差保持不变；类型3为参数均值和标准差都随深度的增加而增大。李典庆等[14]指出cu沿深度方向上的分布规律更加符合服从类型2。cu表示为

cu=a+bz+σU。

(1)

式中：a,b,σ为常数;z表示深度(m);变量U为任意一个均值为0、方差为1的随机变量，变量U的分布也决定了cu的概率分布特征。

表1不排水抗剪强度参数变异系数统计[12]
Table1Statisticsofcoefficientofvariationofundrainedshearstrength[12]

变异系数COV来源18%(海积土)，16%(伦敦黏土)Lumb(1966)18%～30%(纽约黏土)Asaoka和Grivas(1982)5%～50%Lee等(1983)Lacasse和Nadim(1996)21%～23%Soulie等(1990)4%～44%(黏土)，8%～38%(粉土)Phoon和Kulhawy(1999)13%～40%Duncan(2000)0～33%(黏土)Al⁃Homoud和Tanash(2001)5%～55%Uzielli等(2007)6%～80%Srivastava(2010)

图1 cu随深度变化的3种类型Fig.1 Three types of variation of cu against depth

3 稳定系数法

在大量模型试验的结果的基础上，1967年B. B. Broms等[2]最早提出了开挖面稳定系数的概念，建立了适用于描述不排水黏土中垂直开挖面稳定状态的计算表达式,即

(2)

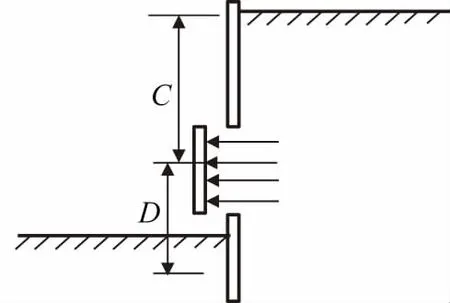
图2 无衬砌的垂直开挖面模型Fig.2 Unsupported opening in vertical hold

式中：N为开挖面稳定系数；σs为地面荷载；σt为开挖面支护应力，假设支护应力为均布力；γ为隧道轴线处的土体重度；C为隧道埋深；D为隧道直径。简化模型如图2所示。通过对现场多个基坑及隧道工程的实测统计分析及简单的室内模拟试验可以发现，当N>6时开挖面开始出现失稳破坏[15]。

4 开挖面稳定概率分析方法

从式(2)中可以看出，计算稳定系数N所涉及的土性参数包括土体重度γ和不排水抗剪强度cu。Phoon等[16]统计大量试验数据得出，土体重度γ的变异性较小，其变异系数一般<0.1，因此可以不考虑土体重度的变异性对盾构隧道开挖面稳定性的影响。如式(1)中所示，假设cu为一随机变量，服从对数正态分布[10]。由概率论可知，对于任意一个服从对数正态分布的随机变量X的累积分布概率Pf可以表示为

(3)

式中：Φ表示标准正态分布的累积概率分布函数；μlnX和σlnX分别表示变量lnX的均值和标准差，其中lnX服从正态分布。将随机变量X用开挖面稳定系数N替换，变换式(2)就可以得到变量lnN的均值μlnN和标准差σlnN分别为：

μlnN=ln[σs+γ(C+D/2)-σt]-μlncu;

(4)

σlnN=σlncu。

(5)

式中μlncu和σlncu分别为变量lncu的均值和方差。由正态分布函数和对数和正态分布函数之间的转换关系可知：

(6)

(7)

式中COVcu表示cu的变异系数，等于其标准差σcu与均值μcu的比值。由式(3)—式(7)可知，开挖面发生失稳破坏的概率可以表示为

Pf=P(N>6)=

(8)

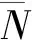
(9)

首先不考虑cu的均值随深度变化的情况，即式(1)中线性系数b=0。取γ=18 kN/m3,C/D=1,C=10 m,μcu=40 kPa,σs=0(不考虑地面荷载的作用)。当作用于开挖面的支护应力σt取值不同时，则可以得到不同的平均稳定系数，由式(9)就可以得到不同不排水抗剪强度参数变异系数COVcu下的隧道开挖面失稳概率随平均稳定系数的变化规律曲线，如图3所示。

图3 不同变异系数下平均稳定系数的概率分布Fig.3 Probability distribution against mean stability coefficient in the presence of varying coefficient of variation

下面研究cu的均值在深度上的变化,即式(1)线性系数b的变化对开挖面失稳概率的影响。在cu的标准差随深度不变的情况下，由于cu的均值随深度线性增大，导致cu的变异系数COVcu随深度逐渐减小。因此本部分采用地表处的变异系数COVcu0进行定量表示，其定义式为σ/μcu0。与图3中各参数取值相同，变化线性系数b的大小，如图4给出了不同COVcu0下失稳概率Pf与无量纲参数γD/σt之间变化关系。

图4 不同COVcu0下的失稳概率Pf与无量纲参数 γ D/σt之间关系曲线Fig.4 Variation of failure probability Pf against dimensionless parameter γ D/σt in the presence of different COVcu0

随着COVcu0的增大，线性系数b对失稳概率的影响差异逐渐减小。保持COVcu0和γD/σt不变，Pf随着b的增大而逐渐降低。从工程设计的角度来说，要求工程发生失稳概率不能过高，例如欧洲岩土规范[17]要求失稳概率不宜超过5%。

取Pf=5%，求得不同工况组合下的支护应力值(用无量纲参数γD/σt替代)，如图5所示。显然，随着COVcu0的增大，γD/σt逐渐减小，相应的所需的支护应力σt也就越大。这表明土体参数变异程度越高，工程发生失稳破坏的概率也就越大。

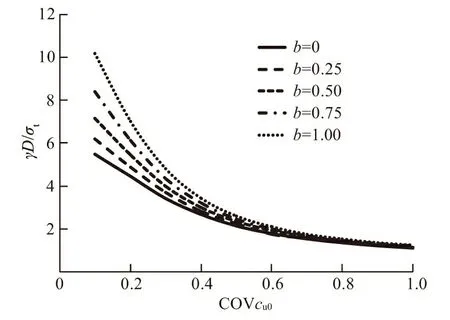
图5 Pt=5%时所对应的无量纲参数γ D/σtFig.5 Dimensionless parameter γ D/σt when failure probability Pt=5%

4 结 论

基于B. B. Broms等提出的开挖面稳定系数的概念，结合概率分析方法，考虑了土性参数的空间变异性，将黏土参数不排水抗剪强度看作服从对数正态分布的随机变量，形成了盾构隧道开挖面稳定概率分析法，讨论了不排水抗剪强度的变异系数和其均值随深度线性增加的特征对开挖面失稳概率的影响规律。研究结果表明:黏土参数不排水抗剪强度的空间变异性对盾构隧道开挖面稳定性有着重要的影响;参数变异程度越高，开挖面发生失稳破坏的概率也就越大，即忽略土性参数的空间变异性会在一定程度上高估开挖面的稳定性。保持不排水抗剪强度的变异系数和开挖面支护应力不变;开挖面失稳概率随着不排水抗剪强度均值线性变化系数的增大而逐渐降低。

从以上研究结果可以看出，单一的开挖面稳定系数很难恰当地反映盾构隧道开挖面的稳定性状态，而采用失稳概率的表示方法更为合适。

[1] 缪林昌, 王正兴, 石文博. 砂土盾构隧道掘进开挖面稳定理论与颗粒流模拟研究[J]. 岩土工程学报, 2015, 37 (1):98-104.

[2] BROMS B B, BENNERMARK H. Stability of Clay at Vertical Openings[J]. Journal of Soil Mechanics and Foundation Engineering Division, 1967, 93(1): 71-94.

[3] HORN M.Horizontal Earth Pressure on Perpendicular Tunnel Face[C]∥Proceedings of the Hungarian National Conference of the Foundation Engineer Industry, Budapest, Hungary, November 7-16, Hungary, 1961.

[4] MAIR R J. Centrifugal Modelling of Tunnel Construction in Soft Clay[D]. UK: Cambridge University Engineering Department 1978.

[5] 陈仁朋, 李 君, 陈云敏,等. 干砂盾构开挖面稳定性模型试验研究[J]. 岩土工程学报, 2011, 33(1):117-122.

[6] 朱 伟, 秦建设, 卢廷浩. 砂土中盾构开挖面变形与破坏数值模拟研究[J]. 岩土工程学报, 2005, 27(8):897-902.

[7] LUMB P. Spatial Variability of Soil Properties[C]∥Proceedings of the Second International Conference on Application of Statistics and Probability in Soil and Structural Engineering, Aachen, Germany. 1975: 397-421.

[8] 李志华, 华 渊, 周太全,等. 盾构隧道开挖面稳定的可靠度研究[J]. 岩土力学，2008，29(增1): 315-319.

[9] MOLLON G, DIAS D, SOUBRA A H. Probabilistic Analysis of Pressurized Tunnels Against Face Stability Using Collocation-based Stochastic Response Surface Method[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(4): 385-397.

[10] MOLLON G, DIAS D, SOUBRA A H. Range of the Safe Retaining Pressures of a Pressurized Tunnel Face by a Probabilistic Approach[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(11): 1954-1967.

[11] ESHRAGHI A, ZARE S. Face Stability Evaluation of a TBM-driven Tunnel in Heterogeneous Soil Using a Probabilistic Approach[J]. International Journal of Geomechanics, 2014, 15(6),doi:10.1061(ASCE)GM. 1943-5622.0000452.

[12] 蒋水华. 水电工程边坡可靠度非侵入式随机分析方法[D]. 武汉:武汉大学, 2014.

[13] LUMB P. The Variability of Natural Soils[J]. Canadian Geotechnical Journal, 1966, 3(2):74-97.

[14] LI D Q, QI X H, PHOON K K,etal. Effect of Spatially Variable Shear Strength Parameters with Linearly Increasing Mean Trend on Reliability of Infinite Slopes[J]. Structural Safety, 2014, 49:45-55.

[15] 韦良文, 张庆贺, 孙统立,等. 盾构隧道开挖面稳定研究进展[J]. 重庆交通大学学报(自然科学版), 2007,26(6):67-72.

[16]PHOON K K,KULHAWY F H.Characterization of Geotechnical Variability[J].Canadian Geotechnical Journal, 1999, 36(4): 612-624.

[17] BS EN 1997-1:2004, EN1997-1 Eurocode 7: Geotechnical Design-Part 1: General Rules[S]. Brussels: European Committee for Standardization, 2005.

Probability Analysis of Face Stability in Shield TunnellingBased on Stability Ratio

CHENG Hong-zhan1,2,3，CHEN Jian1,2,3，HU Zhi-feng1,2,3，HUANG Jue-hao1,2,3

(1.Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan 430071, China; 2.State Key Laboratory of Geomechanics and Geotechnical Engineering, Chinese Academy of Sciences, Wuhan 430071, China; 3.University of Chinese Academy of Sciences, Beijing 100049, China)

A probabilistic method for the stability of shield tunnelling face is proposed based on the concept of stability ratio defined by B. B. Broms and H. Bennermark in consideration of the spatial variability of soil parameters. The undrained shear strength of clay is regarded as a stochastic variable following lognormal distribution, and the failure probability of excavation face affected by the linear increases of variation coefficient and mean value of undrained shear strength against depth is analyzed. Results indicate that the spatial variability of undrained shear strength has a significant effect on face stability. The probability of failure increases correspondingly as coefficient of variation increases, but decreases with the growing of linear coefficient of the mean undrained shear strength. Probabilistic method is more suitable in evaluating the face stability of shield tunnelling than single face stability ratio.

tunnel; face stability; stability ratio; spatial variability; probabilistic method

2016-09-28;

2016-10-29

中国科学院百人计划项目(KZZD-EW-TZ-12)；中国科学院科技服务网络计划项目(STS)(KFJ-EW-STS-122)

程红战(1990-)，男，山东菏泽人，博士研究生，主要从事随机场理论及其在盾构隧道变形和开挖面稳定性应用方面的研究。E-mail:cheng2217@126.com。

10.11988/ckyyb.20161002

TU442

A

1001-5485(2018)01-0133-04

(编辑：赵卫兵)