基于流量-面积比值的小流域设计洪水计算方法对比研究
2018-01-10,,,,,,
,, ,, ,,
(1.长江科学院 重庆分院,重庆 400026;2.武汉长江科创科技发展有限公司 重庆分公司,重庆 400026)
基于流量-面积比值的小流域设计洪水计算方法对比研究
幸新涪1,周火明1,秦维2,谭昭娣2,卢宇2,张乾柱1,卢阳1
(1.长江科学院 重庆分院,重庆 400026;2.武汉长江科创科技发展有限公司 重庆分公司,重庆 400026)
为确定分布式模型法、地区瞬时单位线法及推理公式法在估算山区小流域设计洪水过程中的适用性,基于洪峰流量-流域面积比值,以重庆市綦江区蒲河水系为研究对象,采用3种方法分别进行设计洪水计算,并与重庆市实测100 a一遇洪峰流量进行对比。结果表明:①当流域面积<10 km2时,采用推理公式法更合理可靠;此时河道坡度较大,流域的产、汇流条件符合推理公式法假定条件,计算结果符合实际。②当流域面积为10~100 km2时,分布式模型法与地区瞬时单位线法均可合理计算设计洪水,但前者计算结果比后者更接近实测值。此类流域河道长、坡度平缓,流域的水动力在空间中可视为均匀的扩散;计算格栅单元间连续性强,各栅格向流域出口演算能合理反映真实的设计洪水过程。③当流域面积>100 km2时,3种方法计算结果与实测值均有不同程度的偏离,但分布式模型法偏离程度最低,可作为设计洪水计算的首选方法。研究结果将有助于合理选择设计洪水计算方法,为类似山区小流域设计洪水计算提供参考。
山洪灾害;设计洪水;分布式模型法;地区瞬时单位线法;推理公式法
1 研究背景
山洪系指发生在流域面积小的溪沟或周期性流水的荒溪中快速、强大的地表径流,具有暴涨暴落、破坏力大等特点,往往导致道路和桥梁毁坏,水坝、山塘溃决,甚至造成人员伤亡,形成山洪灾害。集水面积<200 km2的流域常发生山洪灾害[1],而此类流域水文资料往往相对匮乏,无法利用长序列的水文资料进行设计洪水计算,故常用分布式模型法、地区瞬时单位线及推理公式法进行洪水估算。
分布式模型法根据地形资料将研究的流域划分成若干子流域计算单元,按照截留、地表径流、土壤水径流、地下水径流等多种径流成分的汇流特性,沿各单元逐级向流域出口演算。此模型充分考虑了流域降雨、地形、植被以及人类活动等要素对水文过程的影响,也可充分应用传统水文模型的成果与经验,易于建模;但各子流域均有若干参数需要率定[2],尤其在水文资料短缺的小流域地区,参数的率定是分布式模型运用的难题。地区瞬时单位线法以水系生成的随机理论为基础,通过水系中链分布的函数建立流域地貌参数和流速的关系,一定程度上可以反映地貌扩散的物理机制,但缺乏对水动力扩散的科学处理[3]。在汇流时间内,推理公式法假定暴雨强度、径流系数在时间与空间上均匀分布,可以根据不同暴雨条件和流域下垫面细化降雨强度及径流参数,但未能改变假定条件与实际情况不符的差异。
此前,业内学者对3种方法开展了很多研究。孔凡哲等[4]对分布式模型法研究发现,栅格分区会出现坡度为0的情况,且坡度为0的栅格数越多,对洪水结果影响越大;芮孝芳等[5]认为地貌扩散作用取决于流域大小、形状和水系分布状况,水动力扩散作用取决于地形坡度、糙率分布;王国安等[6-7]指出河流槽面面积占比大的平原地区,地区瞬时单位线法比较合理,且认为推理公式法不能用于平原河流和平原河网地区洪水计算;陈家琦等[8]认为流域面积越小越能满足推理公式的假定。这些研究大多是从理论角度对3种洪水设计方法的假定条件及不足作出分析与讨论,并选用较大流域的设计洪水计算结果进行比较,探讨了3种方法的优缺点;但尚未对山区小流域设计洪水计算中3种方法的计算结果合理性及适用范围进行研究。
为研究山区小流域设计洪水计算中分布式模型法、地区瞬时单位线法及推理公式法结果的合理性及适用范围,本文基于重庆市綦江区2015年度山洪灾害调查评价数据,选取典型的山区河流——蒲河流域作为研究对象开展设计洪水计算,将3种方法计算得到的洪峰流量-流域面积比值与重庆市实测100 a一遇洪峰-面积比值[9]进行比较,分析与讨论3种方法计算结果的差异性,确定其适用范围,为同类型山地无资料小流域山洪灾害洪水计算提供参考借鉴。
2 研究对象概况
蒲河位于重庆市綦江区,系綦江第二大支流。该河发源于重庆市万盛区,自东北流向西南,沿途有孝子河、金家河、永丰河等支流依次汇入,流域集水总面积834.7 km2。蒲河地处川东平行岭谷区,地势由东北向西南倾斜,东部又略高于中、西部。流域地形以深丘为主,有部分中、低山。
为讨论3种洪水估算方法在不同特征小流域进行设计洪水计算的适用性,本文选取蒲河水系中流域面积、河道长度及河道坡降不同的10个小流域作为研究对象,合理选取河(沟)道的横断面、纵断面开展实地测点调查与测量,获取流域的特征数据。10个小流域调查点分布位置与编号如图1所示。

图1 蒲河水系及流域测点位置Fig.1 Map of the Puhe river drainage basin and measuring points in the basin
根据实际测点数据,提取测点横断面以上集水面积(下文均用流域面积表述)等相关特征值,如表1所示。其中,测点1、测点5、测点10流域面积均超过100 km2,河道常年活水流动,是蒲河二级或三级支流。其中测点1流域面积最大,为121.24 km2,河道长39.23 km,河道比降0.005 2。测点6—测点9流域面积为25~80 km2,河道长度为10~24 km,河道比降为0.002 8~0.009 6。测点2—测点4流域面积均<25 km2,具有河道短、比降大的特点,为典型的山地干沟。

表1 小流域特征参数Table 1 Characteristic parameters of small catchments
3 设计洪水计算方法及原理
3.1 分布式模型法
分布式模型法是直接基于流域地形地貌及植被特征的单位线计算方法,它以流域水质点汇流时间的概率密度分布函数等价于单位线为理论基础。假定净雨空间分布均匀,首先分析计算小流域中各栅格内径流滞留时间,然后根据汇流路径得到每一点的径流到达小流域出口的汇流时间,最后计算汇流时间的概率密度分布及单位线[10]。
坡地上水流的速度与地形坡度大小有关,还与水量有关。参照曼宁公式,采用考虑坡度和雨强影响的流速公式计算水流在流域某处的速度V:
V=K0S0.5ia;
(1)
Q=AV。
(2)
式中:V为水流速度(m/s);S为流域上某处沿着水流方向的坡度;K0为流速系数,参照分布式中SCS模型研究(1986),本文取值范围为0.3~2.5[11];i为降雨强度(mm/min);a为待定参数,一般取值0.4;Q为流量;A为河道断面面积(m2)。
3.2 地区瞬时单位线法
瞬时单位线的数学基本公式为
(3)
式中:γ为伽马函数,γ(n)=(n-1)!,n相当于水库个数或调节次数;K1为相当于流域汇流时间的参数;n,k为流域单位线的2个模型参数;μ(t)相当于时间变量的瞬时单位线值。
根据计算得到的参数n,k,可得到一个确定的瞬时单位线,它是净雨历时为无限小的μ(0,t)。因此,将μ(0,t)积分转换成积分曲线s(t),即
(4)
对上式进行积分与转换,得无因次时段单位线:μ(Δt,t)=s(t)-s(t-1)。当s(0)=0时,可得到时段为Δt、净雨深度为ΔR的时段单位线;地面净雨过程h(t)与时段单位线q(Δt,t)的卷积即可得还原地面径流过程Qc(t),实际应用时取离散卷积形式,即

(5)
式中:Tu为净雨过程历时;i为第i个净雨历时过程。
3.3 推理公式法
推理公式法以推理成因为基础,结合了经验性参数定量,它从基本的洪水成因出发,假定流域强度在时间、空间上均匀分布,经过线性汇流推导,表达了流域产汇流因素的经验关系。推理公式法表达式为:
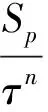
(6)
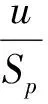
(7)

(8)
式中:Qm,p为频率为P的洪峰流量;ψ为洪峰径流系数;Sp为雨力,即年最大1 h平均雨强;τ为流域汇流时间;n为暴雨公式指数;m为汇流参数;F为流域面积;L为河流长度;J为河道平均比降;μ为损失参数,即产流历时内流域平均入渗强度。
计算过程中,当产流历时tc>τ为全面产流,此时成峰暴雨时段内的雨强都大于下渗率,产流强度都>0;当tc<τ为部分产流,成峰暴雨时段内部分时段的雨强小于下渗率而不产流,在产流历时tc范围内产生的径流全部参与形成洪峰。
4 洪水计算与成果分析
采用3种方法分别计算小流域设计洪水,对比100 a一遇(P=1%)的洪峰流量结果,并拟合与流域面积之间的关系;对比重庆市多场实测洪水数据,比较各计算结果的差异,分析3种方法的优缺点并确定适用范围。
4.1 蒲河流域暴雨参数信息
由于重庆市尚未编制暴雨洪水计算手册,故采用《四川省中小流域暴雨洪水计算手册》(以下简称《手册》)进行流域暴雨计算[12]。根据《手册》查得蒲河流域暴雨时面深关系和设计雨型综合分区,获取典型时段暴雨均值和CV值;按照CS=3.5CV,依据Pearson-III型曲线模比系数Kp值表,计算典型设计频率的设计点雨量;合理选取时段雨量折减系数与点面雨量转换系数,折算设计面雨量[13];按照前期土壤中等湿润,初损雨量15 mm,平均入渗率0.9 mm/h的工况进行设计洪水计算[14]。暴雨参数及成果见表2。

表2 最大1 d降水量设计结果Table 2 Design of maximum daily precipitation inthe study area
注:CS为偏态系数;CV为变差系数
4.2 设计洪峰流量计算结果与分析
100 a一遇设计洪水计算成果见表3。
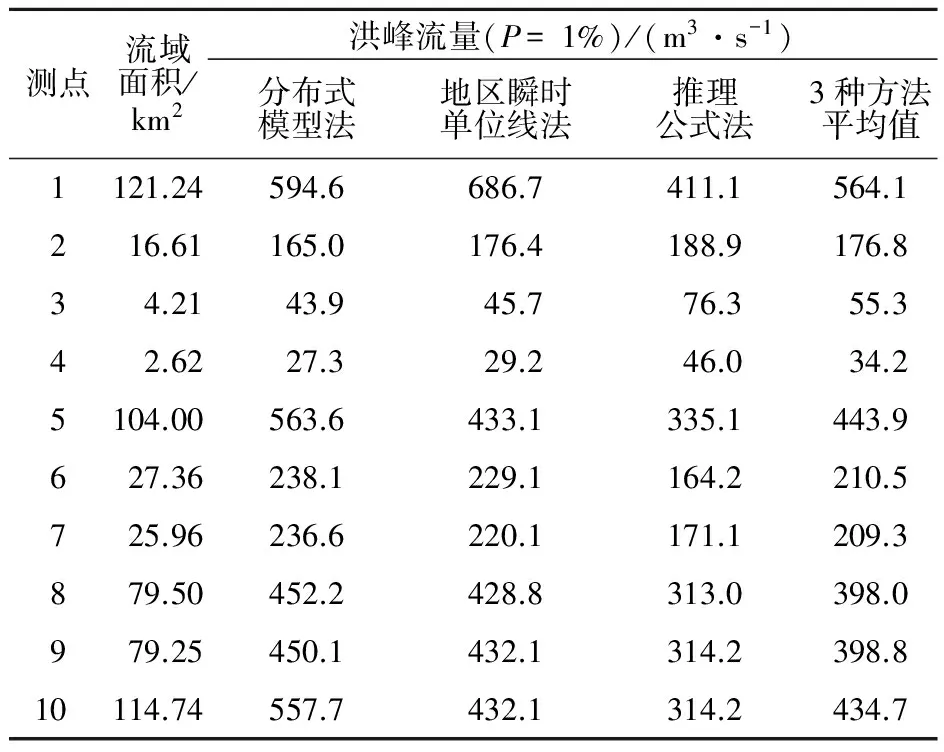
表3 100 a一遇设计洪水计算结果Table 3 Calculation results of 100-year design flood
结果表明,推求不同流域面积P=1%时的设计洪峰流量,3种方法存在较大的差异性。流域面积<20 km2的3个对象中,推理公式法计算值最大。以测点2为例,分布式模型法、地区瞬时单位线法、推理公式法计算的洪峰流量分别为165.0,176.4, 188.9 m3/s,与3种方法平均洪峰流量176.8 m3/s分别相差了6.7%,0.2% ,6.8%,可见地区瞬时单位线法计算值差异小,而另外两种方法偏差较大。
流域面积接近100 km2时,分布式模型法与地区瞬时单位线法计算结果相差不大,而推理公式法计算结果明显小于前两者计算结果。
在流域面积>100 km2的3个对象中,随着流域面积的增加,分布式模型法计算值与其对应的平均值差值分别为26.5%,28.7%,5.4%,可见流域面积越大,分布式模型法相对差异越小。
4.3 流量-面积指数比分析
将表3的洪峰流量与对应流域面积点绘在双对数图上,对数点拟合直线的斜率为流量-面积指数比,与重庆市多年实测100 a一遇(P=1%)洪峰流量-流域面积指数比相关图比较[12],详见图2、图3。

图2 重庆市多年实测100 a一遇洪峰-面积指数比Fig.2 Ratio of measured 100-year flood peak flow to catchment area in Chongqing
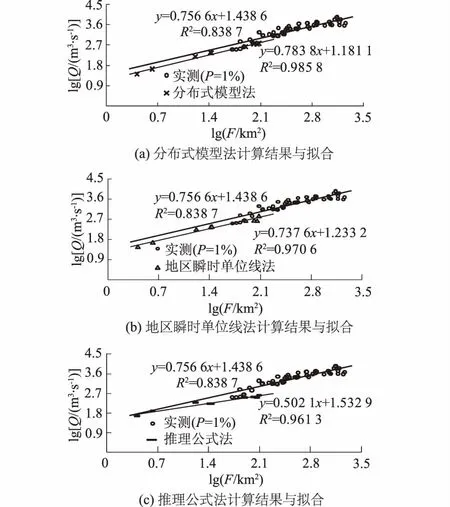
图3 洪峰流量Q与流域面积F双对数曲线拟合Fig.3 Double logarithmic curves of peak flow vs. catchment area
图3(a)中,实测值与分布式模型法计算结果拟合线相关系数R均>0.9,均表现出高度相关性,拟合效果可靠。实测洪峰流量-流域面积对数拟合直线斜率为0.756 6,计算结果拟合直线斜率为0.783 8,两拟合直线近乎平行;各计算结果均靠近实测拟合直线,证明分布式模型法在设计洪水计算时,结果整体符合实际情况。图3(b)中,地区瞬时单位线计算结果拟合直线斜率为0.737 6,与实测值拟合直线斜率相差2.5%,计算结果均靠近实测拟合直线,即该方法进行设计洪水计算结果符合实际。图3(c)推理公式法计算结果与实测值则表现出明显的差异性,具体为在流域面积小时,洪峰流量计算值接近实测值,结果合理;随着流域面积不断增大,计算值越来越偏离实测值,超出实测值分布的区间范围,此时计算结果不合理。
4.4 相对误差分析
为进一步分析各方法计算结果与实测值的差异程度,故采用相对误差指标开展量化分析。相对误差计算公式为
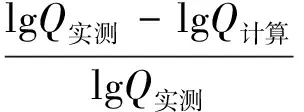
(9)
将10个小流域的流域面积对数值分别代入实测洪水拟合线得到lgQ实测,分别减去3种方法对应的lgQ计算值,最终按照式(9)可以得到相对误差δ。3种方法得到的各流域洪水计算相对误差见图4。
图4中,分布式模型法与地区瞬时单位线的相对误差曲线表现出先下降、后逐步上升的规律,推理公式法的相对误差曲线则呈现单调递增的规律,3条曲线在流域面积10 km2附近相交。当流域面积<10 km2时,推理公式法的平均相对误差为7.5%,明显小于另外2种方法计算结果的相对误差,即推理公式法计算结果更匹配重庆市实测洪水的拟合曲线。此时采用推理公式法进行设计洪水计算更合理。当流域面积>10 km2时,推理公式法相对误差明显大于另外2种方法,推理公式法的设计洪水计算结果偏差明显,此时可考虑分布式模型法与地区瞬时单位线法进行设计洪水计算。
分布式模型法与地区瞬时单位线法相对误差曲线规律相似,但也存在差异性。当流域面积<10 km2时,前者计算结果相对误差略小于后者结果相对误差,即分布式模型法计算结果更接近实测洪峰流量;当流域面积为10~25 km2时,地区瞬时单位线计算结果相对误差较小;当流域面积>25 km2时,地区瞬时单位线法相对误差介于分布式模型法与推理公式法的相对误差曲线之间,比分布式模型法的计算结果更偏离实测值;随着流域面积增大,偏离程度越显著,此时运用分布式模型法计算设计洪水,结果更合理可靠。当流域面积>100 km2时,3种方法的δ曲线均不同幅度上升,表明此时的计算结果均有较大的偏差值,但分布式模型法偏离程度最低。
4.5 3种方法的适用范围
结合小流域的其他特征,探讨3种方法的适用范围。当流域面积<10 km2时,河道平均长度为5 km,平均坡度为8.6%,为典型的山区小流域。此时河流槽面占比小,河槽蓄流能力小,整个流域的产流条件与汇流条件基本相等,实际情况与推理公式法的假定条件匹配度高;故此时采用推理公式法进行设计洪水计算更合理。
当流域面积为10~100 km2时,河道平均长度为16 km,平均坡度为1.7%。由于流域面积较大,坡度平缓,流域的水文响应过程越能得以真实模拟,此时水动力扩散在坡面漫流、坡面-河道交汇及河道行流3个阶段差异不大,可视为在空间均匀扩散,地面径流过程曲线能准确合理反映实际的径流过程,故地区瞬时单位线计算结果合理;同样,在坡度平缓的流域中,划分的计算单元栅格之间的地貌形态及河道坡度均不会发生大的差异性改变,流速在栅格之间整体连续性强,各栅格向流域出口拟合演算的过程能合理反映实际的设计洪水过程,计算的洪峰流量值符合实际情况。
当流域面积>100 km2时,河道平均长度为32 km,平均坡度为0.9%,由于河道长,沿途流经深丘及中、低山等不同地形,地区瞬时单位线法拟合的径流过程以及分布式模型法的各栅格间会出现流域特征突变的情况,这种局部的改变会降低整体结果的合理性,故2种方法的计算结果均不同程度偏离实测值。由于分布式SCS模型的关键问题在于率定参数、调节降雨初损及土壤前期湿润度等,面积较小的流域没有准确资料校正率定参数,其计算结果偏离实际较大;当流域面积增大时,参数率定的准确度增加,降雨初损值也相对可靠,其计算结果更接近实际结果。
5 结 论
本文通过与重庆市实测洪水资料对比,探讨了山区无资料小流域设计洪水计算中分布式模型法、地区瞬时单位线法以及推理公式法计算结果的差异性,并分析了3种方法的适用范围。得到以下结论:
(1) 当流域面积<10 km2时,推理公式法的设计洪水计算结果与实测值偏差7.5%,此时河道坡度较大,流域的产流条件与汇流条件相似,符合推理公式法假定条件,故采用推理公式法更合理可靠。
(2) 当流域面积为10~100 km2时,此类流域面积较大、坡度平缓,流域的水动力在空间中可视为均匀扩散;栅格之间整体连续性强,各栅格向流域出口演算能合理反映真实的设计洪水过程。故分布式模型法与地区瞬时单位线法均可合理计算设计洪水,但前者计算结果比后者更接近实测值。在精度要求较高的情况下,优先考虑采用分布式模型法进行设计洪水计算;若力求计算简便,可优先考虑采用地区瞬时单位线法。
(3) 当流域面积>100 km2时,山区河流往往流经深丘及中、低山等不同地形,流域局部之间差异明显,3种方法计算结果与实测值均有不同程度的偏离,但分布式模型法偏离程度最低,可作为设计洪水计算的首选方法。
[1] 全国山洪灾害防治项目组.山洪灾害分析评价技术要求[R].北京:全国山洪灾害防治项目组,2015.
[2] 张红萍.山区小流域洪水风险评估与预警技术研究[D].北京: 中国水利水电科学研究院,2013.
[3] 芮孝芳.地貌瞬时单位线研究进展[J].水科学进展,1999,10(3):345-350.
[4] 孔凡哲,韩继伟,赵 磊,等.分布式单位线分析方法的对比分析[J].人民黄河,2011,33(1):28-30.
[5] 芮孝芳,石 朋.基于地貌扩散和水动力扩散的流域瞬时单位线研究[J].水科学进展,2002,13(4):439-444.
[6] 王国安,贺顺德,李超群,等.论广东省综合单位线的基本原理和适用条件[J].人民黄河,2011,33(3):15-18.
[7] 王国安,贺顺德,李荣容,等.论推理公式的基本原理和适用条件[J].人民黄河,2010,32(12):1-4.
[8] 陈家琦,张恭肃.小流域暴雨洪水计算[M].北京:水利电力出版社,1985.
[9] 彭万兵,赵 东.重庆市万州区山洪灾害分析评价报告[R].重庆:长江上游水文水资源勘测局,2015.
[10] 芮孝芳.水文学原理[M].北京:中国水利水电出版社,2004.
[11] 范姝云.基于SCS模型的尖山河小流域不同土地利用类型地表径流及COD污染负荷研究[D].昆明:西南林业大学,2015.
[12] 四川省水利厅.四川省中小流域暴雨洪水计算手册[K].成都:四川省水利厅,1984.
[13] 四川省水利厅.四川省暴雨洪水图集[K].成都:四川省水利厅,2011.
[14] 詹道江,叶守泽.工程水文学[M].北京:中国水利水电出版社,2000.
Comparison of Calculation Methods for Design Flood ofSmall Catchments Based on Flow-Area Ratio
XING Xin-fu1, ZHOU Huo-ming1, QIN Wei2, TAN Zhao-di2, LU Yu2, ZHANG Qian-zhu1, LU Yang1
(1.Chongqing Branch, Yangtze River Scientific Research Institute, Chongqing 400026, China; 2.Chongqing Branch of Wuhan Changjiang Kechuang Technology Development Co., Ltd., Chongqing 400026, China)
The design flood in a mountainous small catchment was calculated by using distributed model, regional instantaneous unit hydrograph, and deducted formula respectively based on the ratio of peak discharge to catchment area, and the calculated results were further compared with the measured peak discharge of 100-year flood to determine the applicability of the above-mentioned three methods. Puhe river system in Qijiang, Chongqing was selected as a case study. Conclusions are drawn as follows: 1) deducted formula is more accurate and reliable for catchment with an area smaller than 10 km2as steep river slope makes the runoff yield and concentration condition consistent with the assumption of the deducted formula; 2) distributed model and regional instantaneous unit hydrograph are both applicable to catchment with an area between 10-100 km2, with the result of the former closer to measured result; in such catchment of long channel and gentle slope, the hydrodynamic dispersion can be regarded as uniform diffusion in space, and the computation grid units are strongly continuous, well reflecting the real design flood process; 3) distributed model is recommended as the preferred method when catchment area is larger than 100 km2, as it deviates to the smallest extent to the measured value among the three methods. The conclusions will be helpful to the selection of a reasonable calculation method.
mountain flood disaster; design flood; distributed model; regional instantaneous unit hydrograph; deducted formula
2016-09-13;
2016-11-10
中央级公益性科研院所基本科研业务费专项项目(CKSF2016034/CQ)
幸新涪(1992-),男,重庆万州人,助理工程师,硕士,研究方向为山洪灾害与防治。E-mail:xing_xinfu1992@163.com
卢 阳(1982-),男,湖北汉川人,高级工程师,博士,研究方向为山地灾害形成机理与防治技术。E-mail:crsrily@163.com
10.11988/ckyyb.20160943
P333
A
1001-5485(2018)01-0057-06
(编辑:罗 娟)
