断层力学与几何参数对岩质边坡稳定性的影响

， ，,，

(中国地质大学(武汉) 工程学院，武汉 430074)

断层力学与几何参数对岩质边坡稳定性的影响

和大钊，胡斌，姚文敏,李华舟，毛元静

(中国地质大学(武汉) 工程学院，武汉 430074)

采用FLAC3D强度折减法并对比slide极限平衡法，分别研究断层破碎带岩土体的泊松比、抗拉强度、内聚力和内摩擦角等力学参数及断层的断距、厚度、倾角、相对临空面的距离等几何参数对岩质边坡破坏模式和稳定性的影响。结果表明：边坡的稳定性随内聚力的增大而增大,且基本不受泊松比和抗拉强度的影响，2种方法得出的内摩擦角对边坡的稳定性影响规律有所不同；断层的几何参数对边坡的破坏模式和稳定性有较大的影响，并且影响程度大于其力学参数的影响。

岩质边坡;断层；力学参数；几何参数；破坏模式；边坡稳定性

1 研究背景

岩体在漫长的地质演化过程中，内部会形成大量的断层、节理[1]。断层是构造运动中广泛发育的构造形态，它大小不一、规模不等，断层带内岩土体力学性质较差[2]，断层的存在破坏了岩层的连续性和完整性。大量工程实践表明，岩质边坡由于含断层而使得自身的变形破坏模式及稳定性问题变得复杂而多样，其失稳多是由于其内部的节理、裂隙等缺陷及其发展导致的[3-5]，给露天矿开采等生产活动带来较大的安全隐患[6]。

近年来，诸多学者针对地下煤层、储油层等采用数值模拟方法研究了断层对地应力的影响[7-9]，而断层对岩质边坡的稳定性影响等方面的研究[10-12]相对较少。鉴于此，本文采用数值模拟手段研究断层的力学参数和几何参数对边坡稳定性和破坏模式的影响规律，为该类边坡工程稳定性评价提供借鉴。

2 模拟方案

2.1 数值模型的建立

数值计算模型以四川峨胜某露天采石灰石矿山边坡为原型。该边坡岩性主要为二叠系灰岩，内部存在F1和F22条断层，其中F1断层为较早的断层，F2断层为较新的断层，F1断层与边坡走向基本一致，F2断层与边坡走向斜交。相应的岩石力学试验及钻孔资料显示，随着边坡的开挖，沿边坡走向不同部位的断层破碎带岩土体力学参数和断层几何参数有所变化。边坡剖面示意如图1，其中D=3 m,L=40 m,θ=60°,S=40 m，模型未考虑局部开挖台阶的影响。

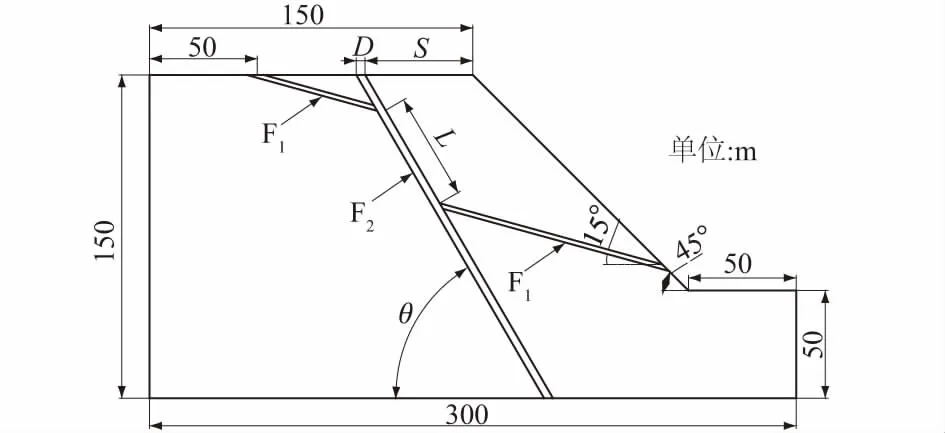
图1 边坡模型示意图Fig.1 Schematic diagram of slope model

弱化法和Interface命令法是FLAC断层模拟中的2类基本方法[13-14]，本次研究选用的是弱化法。基本假设：岩体为均匀各向同性材料；断层为完全弹性材料；断层仅仅受到现代构造应力场作用,古构造应力场对断层产生的残余应力忽略不计。利用有限元软件ANSYS建立边坡模型，为消除尺寸效应并考虑到单元数量对于计算效率的影响，确定模型划分单元的尺寸约为计算模型的1/10～1/20，将模型导入到FLAC3D软件中进行计算，边界条件为底部固定约束，四周采用法向约束，上部为自由边界。

2.2 计算方法

计算选用能同时考虑关联流动拉伸屈服和非关联流动剪切屈服的Mohr-Coulomb屈服准则，采用FLAC3D内置的强度折减法计算边坡的稳定性系数，以边坡临界破坏(即计算不收敛)时的x方向位移云图与位移矢量图进行分析。

3 断层破碎带力学参数对边坡的影响

3.1 力学参数的选取

选取对岩土体力学性质影响较大的4种力学参数，即断层破碎带岩土体的泊松比、抗拉强度、内聚力和内摩擦角，首先根据相关断层破碎带物质的力学试验结果及工程经验确定每种力学参数的常见范围，然后对该范围进行适当扩宽作为极端范围，在极端范围内进行内插取值作为计算参数，图1所示剖面位置的岩土体力学参数取值如表1所示。

表1 力学参数Table 1 Mechanical parameters

3.2 数值模拟结果

采用控制变量法分别改变表1中F1和F2断层破碎带岩土体的泊松比、抗拉强度、内聚力和内摩擦角，在研究其中某一参数时，保持其他参数为表1中的数值不变。由FLAC3D软件计算其稳定性，结果如图2所示。可以看出，断层的存在切断了应力的传递路径，变形运动主要为2断层面与临空面之间的楔形体顺层滑移，F2断层出露部位的变形量最大。不同力学参数下计算所得的边坡x方向位移云图和位移矢量图均与图2相似(位移大小不同)，说明力学参数的改变不会改变边坡的破坏模式。

边坡稳定性随力学参数的变化见图3。由于极限平衡法只考虑抗剪强度参数，因此只对内摩擦角和内聚力采用slide软件进行对比研究。

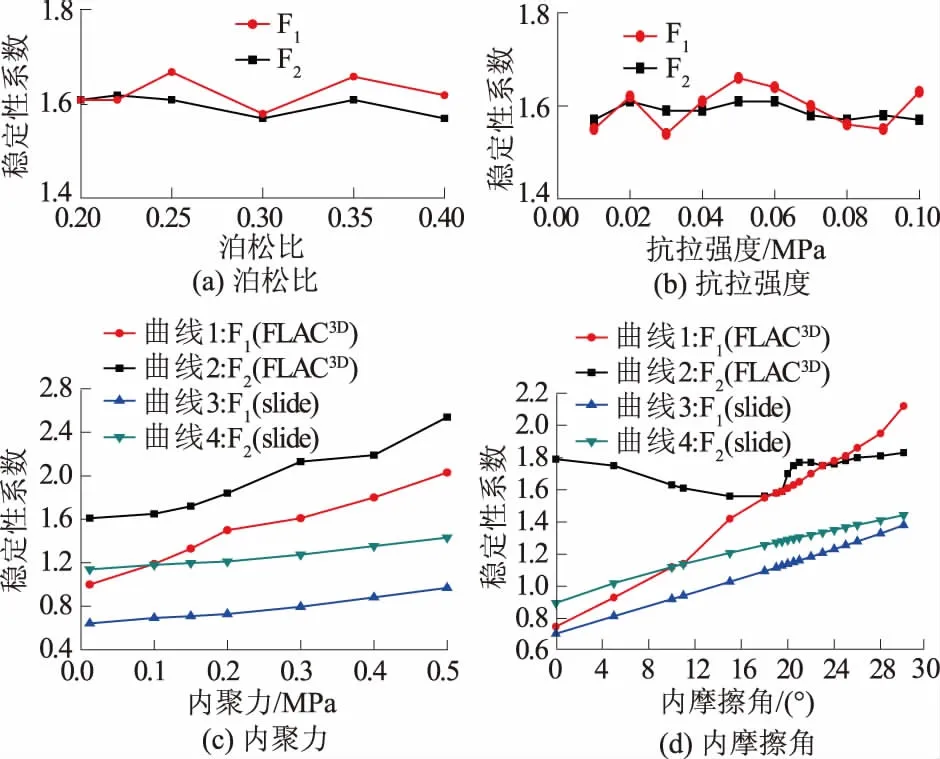
图3 稳定性系数随力学参数变化Fig.3 Variation of stability coefficient with mechanical parameters

3.3 模拟结果分析

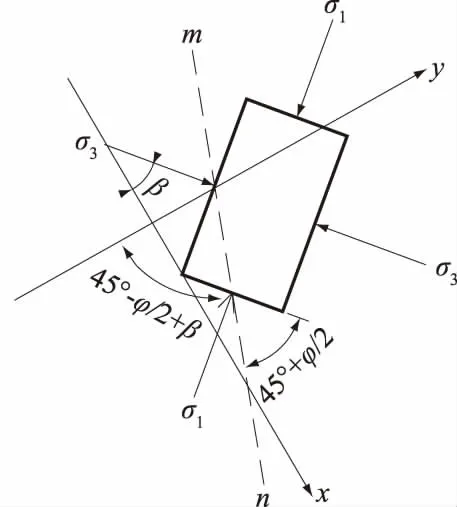
图4 单元体受力分析Fig.4 Mechanics analysis of unit

由图3(a)、图3(b)可知F1和F2断层破碎带岩土体的泊松比和抗拉强度对边坡稳定性影响都很小；由图3(c)可知边坡稳定性随内聚力的增大而增大，并且由slide软件极限平衡法比FLAC3D软件强度折减法的计算结果更加保守且敏感性相对较低；由图3(d)可知，由slide软件算得的边坡稳定性随2断层破碎带岩土体内摩擦角增大而增大，这与由FLAC3D软件计算所得的F1断层曲线的趋势是一致的。上述规律符合预期并且也与前人的研究成果一致，而由FLAC3D软件计算所得的F2断层曲线的变化趋势为先减小后增大最后基本保持不变，对该现象的原因分析为：在F1或F2断层破碎带内取一单元体(图4)进行受力分析，可以确定在垂直纸面方向内单元体受到的法向约束力为正应力σ2，则最大主应力σ1和最小主应力σ3必在平行纸面的平面内，以断层倾向方向为x轴，垂直断层面方向为y轴建立如图所示的坐标系，假设σ3与断层面的夹角为β。

由弹塑性力学知识可知单元体的破坏面mn面,即剪应力τ所在平面与最大主应力σ1作用面的夹角为45°+φ/2，其中

τ=c+σtanφ。

(1)

由几何关系可得剪应力τ所在平面与y轴的夹角为45°+φ/2+β，将τ分解为τx和τy，则∑τx提供了对断层面右侧岩土体的摩擦力或抗滑力，由图4可知τx=τ·sin(45°-φ/2+β)，则

τx=(c+σ·tanφ)·sin(45°-φ/2+β) 。

(2)

对曲线2(图3(d))进行分析，当F2断层带的内摩擦角φ<20°时，边坡破坏首先开始于F2断层带，单元体所受σ值较小;当φ<15°时，σtanφ远小于内聚力c，式(2)可简化为τx=csin(45°-φ/2+β)，此时随着φ的增大，τx逐渐减小，抗滑力减小，因此边坡稳定性曲线呈现递减的趋势。而当τx>16°时，σtanφ不可忽略，此时式(2)为增函数，τx随着φ的增大而增大，抗滑力增大，因此边坡稳定性曲线呈现递增趋势。随着φ继续增大至21°时，模型的破坏将会首先发生在F2断层带部位，稳定性主要由F2断层带的力学性质决定，因此当φ继续增大时，边坡稳定性系数基本不再变化。

对曲线1(图3(d))进行分析，由于F1断层带内单元体所受的σ值较大，σtanφ不可忽略，此时式(2)为增函数，τx随着φ的增大而增大，抗滑力增大，因此边坡稳定性曲线呈现递增趋势。

4 断层几何参数对边坡的影响

4.1 几何参数的选取

由于F2断层与边坡走向斜交，不同部位剖面显示的断层相对临空面的距离S将产生连续变化，同时本次研究还模拟了F2断层不同厚度D、断距L、倾角θ等情况下的边坡稳定性。在图1模型的基础上采用控制变量法分别改变F2断层的D,L,θ,S4种几何参数，选取的计算力学参数仍如表1所示。

4.2 断层的断距对边坡的影响

在断距-80～90 m范围内分别建立14种不同断距的模型，部分模型如图5，计算所得部分位移云图和矢量图如图6。

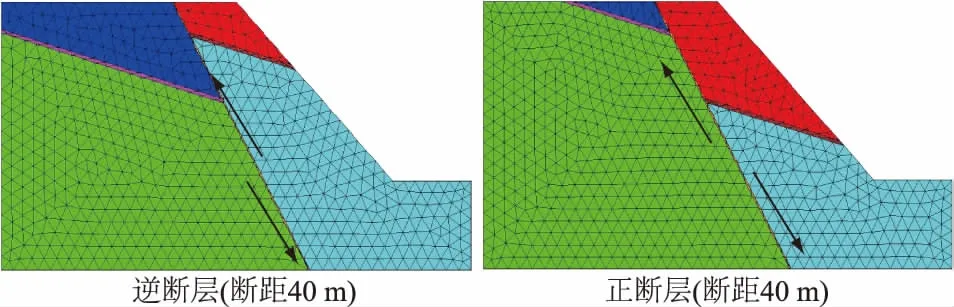
图5 不同断距FLAC3D模型Fig.5 Diagrams of FLAC3D model with different fault throws

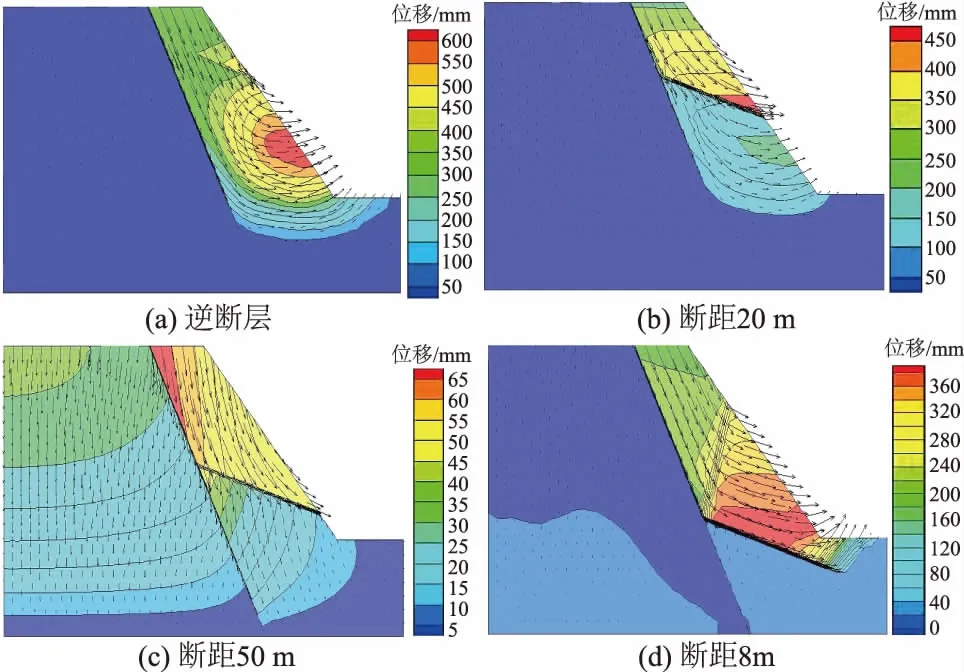
图6 不同断距下位移云图与矢量图Fig.6 Cloud and vector graph of displacement of model with different fault throws

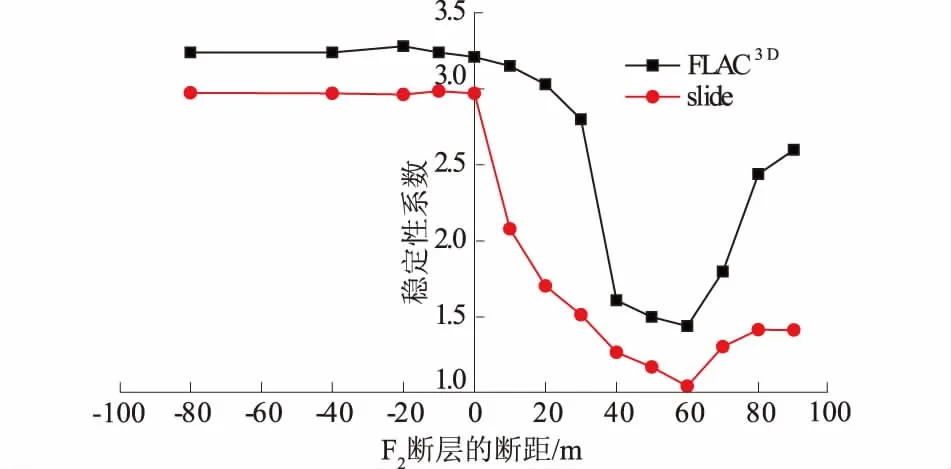
图7 稳定性系数随断距的变化Fig.7 Variation of stability coefficient with fault throw

由图6(a)可知，当F2断层为逆断层或走滑断层(断距为0m)时，F1断层的存在对边坡的变形运动基本无影响，断层面右侧岩土体向临空面发生滑移-压致拉裂，坡脚处的变形运动最剧烈。当F2断层为正断层时，变形运动主要为楔形体顺层滑移、楔形体下部岩体滑移-压致拉裂或两者组合变形运动。

将边坡稳定性系数绘制成图7所示的变化趋势图，由图7可知：逆断层的断距对边坡稳定性基本无影响，而正断层的断距对边坡稳定性影响较大，随正断层断距的增大，边坡的稳定性系数呈现出先减小后增大的趋势，断距为60m时边坡的稳定性最差。

分析原因为：由经验可知坡角为45°的边坡剪出口位置在坡脚上方附近，F1断层的存在会加剧边坡的剪出破坏，其出露位置距离剪出口越近且上部楔形体体积越大则边坡稳定性越差。而当F2为逆断层时，F1断层出露位置距离剪出口较远且保持不变，因此其稳定性系数较高且保持基本不变。综上所述，F2断层的断距通过改变F1断层的出露位置与楔形体的体积从而改变边坡的稳定性。

4.3 断层的倾角对边坡的影响

在图1模型的基础上分别建立6种不同断层倾角的边坡模型，部分模型如图8，所得位移云图与矢量图如图9所示。当F2断层倾角<15°即与F2断层平行时，由于F2断层带的力学参数比F1断层更差，因此边坡首先沿F2断层面产生顺层滑移。当F2断层倾角为30°时，F2断层右侧楔形体不足以抵挡左侧楔形体向临空面的运动，因此产生如图9(b)所示的变形运动。当F2断层倾角>30°时，F2断层左侧楔形体不能向临空面运动，因此只有右侧楔形体发生顺层滑移。

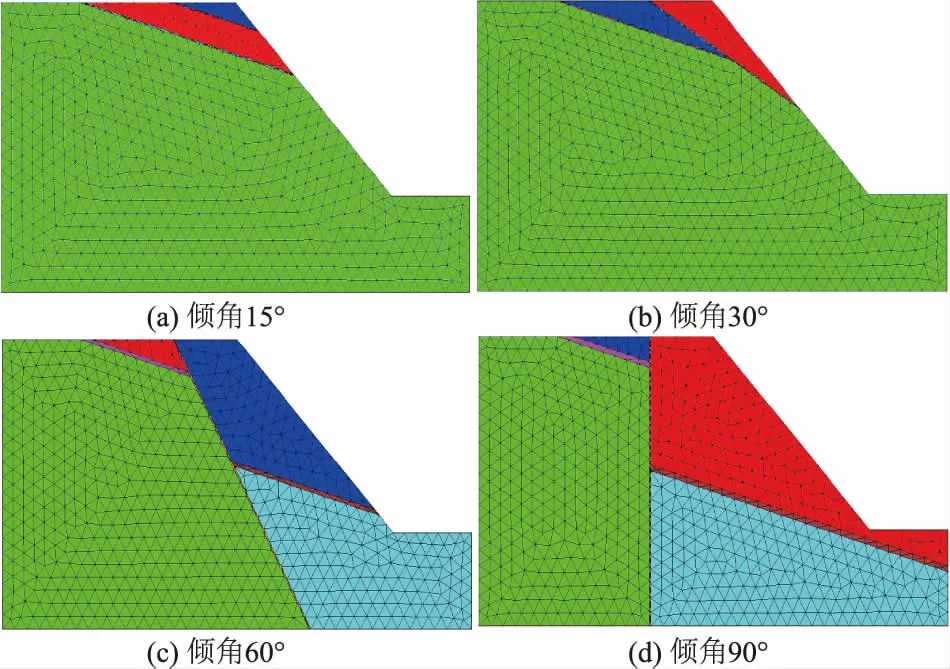
图8 不同倾角FLAC3D模型Fig.8 Diagrams of FLAC3D model with different dips

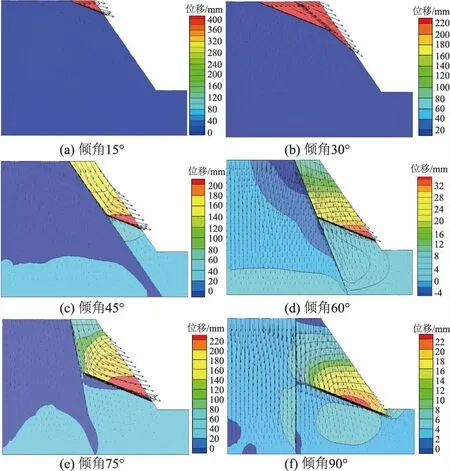
图9 不同倾角下位移云图与矢量图Fig.9 Cloud and vector graph of displacement of model with different dips

将边坡稳定性系数绘制成如图10所示的变化趋势图，随着断层倾角的增大，边坡稳定性系数呈现先增大后减小再增大的趋势，当断层倾角约为15°或60°时边坡的稳定性最差。

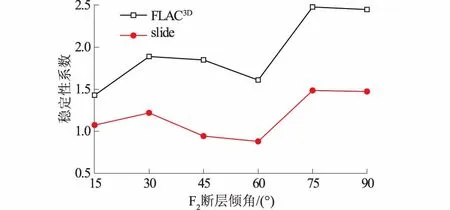
图10 稳定性系数随断层倾角的变化Fig.10 Variation of stability coefficient with dips

4.4 断层的厚度对边坡的影响

本次研究选用弱化法模拟断层，断层部位的力学参数是在其周围岩土体的力学参数条件下进行适当折减得到的，这种方法可以通过改变模型中断层部位的宽度从而模拟不同的断层厚度D，这也是弱化法相对Interface命令法的优势之一。本次研究通过在图1模型基础上改变F2断层的厚度共建立了5个模型，计算结果见表2，可知在所研究的范围内，断层厚度对边坡的破坏模式及稳定性影响很小。

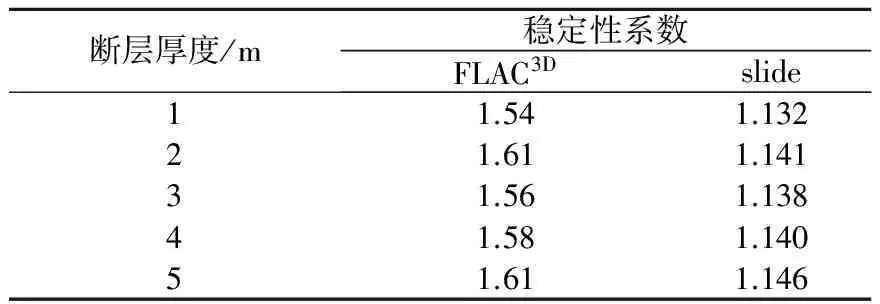
表2 不同断层厚度下的边坡稳定性系数Table 2 Stability coefficient of slope with differentthickness of fault

4.5 断层相对临空面的距离对边坡的影响

在图1模型基础上将边坡的宽度由300 m扩大至500 m，在10～300 m范围内改变F2断层相对临空面的距离共建立11个模型，计算所得部分位移云图与矢量图如图11。

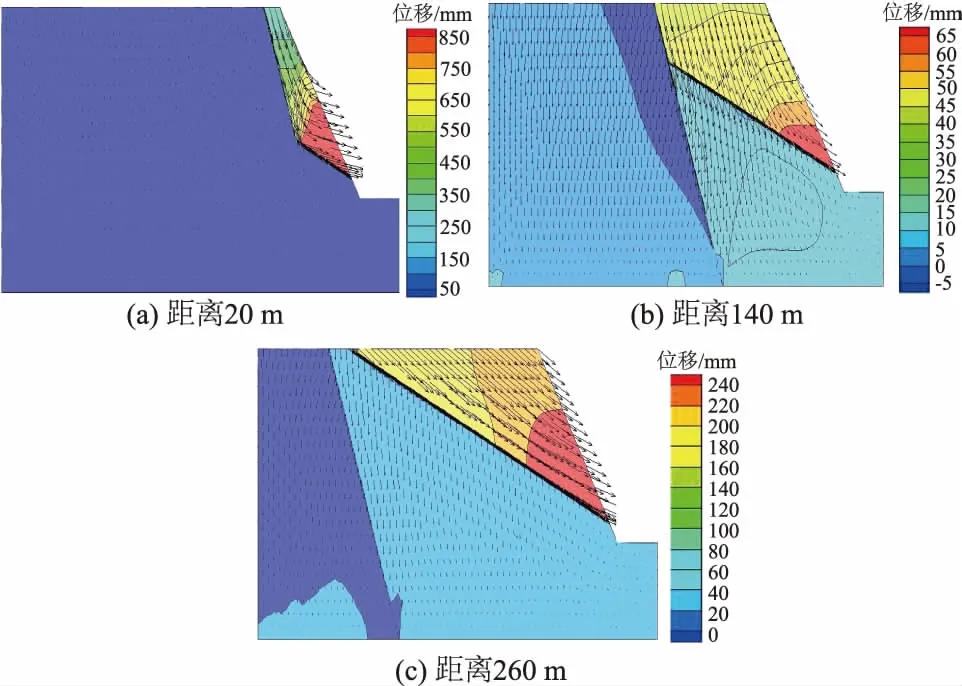
图11 不同相对临空面距离下位移云图与矢量图Fig.11 Cloud and vector graph of displacement of model with different distances from free face

当F2断层相对临空面的距离<40 m时，右侧楔形体在自重应力作用下向下挤压发生滑移-压致拉裂；当F2断层相对临空面的距离>40 m时，右侧楔形体沿F2断层整体顺层滑移。边坡稳定性随断层相对临空面距离的变化趋势如图12。

由图12可知：当距离<30 m时，楔形体的体积逐渐增大，抗滑力增幅小于下滑力增幅导致剩余下滑力减小，稳定性系数亦减小；当距离为30～200 m时，下滑力增幅减小和抗滑力增幅变大导致剩余下滑力增大，稳定性系数亦越来越大；当距离>200 m时，下滑力和抗滑力都不再变化，因此稳定性系数也趋于不变。

通过上述各个稳定性趋势曲线的变化幅度可以看出，几何参数对边坡的影响程度大于力学参数的影响程度。

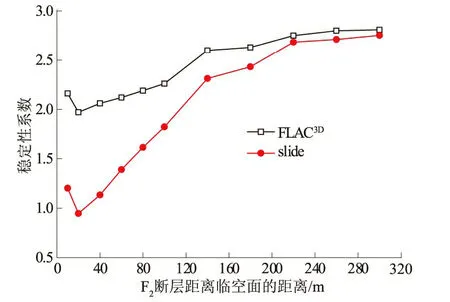
图12 稳定性系数随断层相对临空面距离的变化Fig.12 Variation of stability coefficient with distance from free face

5 结 语

本文运用数值模拟方法研究了含双断层岩质边坡的破坏模式与稳定性系数变化规律，主要结论为：

(1) 断层切断了应力的传递路径，导致边坡变形破坏集中在断层面与临空面之间的楔形体部位。

(2) 力学参数对边坡的影响程度较小；几何参数通过改变楔形体的形状、大小及底部出露位置从而改变边坡的破坏模式和稳定性，并且其影响程度大于力学参数的影响程度。

(3) slide软件极限平衡法相比FLAC3D软件强度折减法的计算结果更加保守，敏感性相对较低，并且由于两者在计算方法上的不同，其计算所得的内摩擦角对边坡稳定性的影响规律也有所差异。

[1] 刘 刚, 赵 坚, 宋宏伟. 节理分布对岩体破坏影响的数值模拟研究[J]. 中国矿业大学学报, 2007, 36(1):17-22.

[2] 江 涛, 徐卫亚, 陈 宏,等. 受断层切割影响的拱坝坝肩岩体三维稳定性数值分析及加固措施模拟[J]. 岩石力学与工程学报,2005, 24(增2):5840-5844.

[3] 王永胜, 郭静芸, 董高峰,等. 辽宁抚顺西露天矿北帮边坡稳定性分析及变形分区[J]. 中国地质灾害与防治学报, 2012,(4):86-93.

[4] 漆祖芳, 姜清辉, 唐志丹,等. 锦屏一级水电站左岸坝肩边坡施工期稳定分析[J]. 岩土力学, 2012, 33(2):531-538.

[5] 王 东, 曹兰柱, 朴春德,等. 露井联采逆倾边坡破坏模式及稳定性评价方法研究[J]. 中国地质灾害与防治学报, 2011, 22(3):33-38.

[6] 尚文凯, 王 东, 曹兰柱,等. 露天矿顺倾层状边坡稳定性的断层效应[J]. 有色金属(矿山部分), 2015, 67(3):92-97.

[7] 贾晓亮, 崔洪庆, 张子敏. 断层端部地应力影响因素数值分析[J]. 煤田地质与勘探, 2010, 38(4):47-51.

[8] 沈海超, 程远方, 赵益忠,等. 基于实测数据及数值模拟断层对地应力的影响[J]. 岩石力学与工程学报, 2008,27(增2):3985-3990.

[9] 马淑芝, 贾洪彪, 易顺民,等. 罗湖断裂带地应力场三维有限元模拟分析[J]. 岩石力学与工程学报, 2006, 25(增2):3898-3903.

[10] 姜耀东, 王 涛, 赵毅鑫,等. 采动影响下断层活化规律的数值模拟研究[J]. 中国矿业大学学报, 2013, 42(1):1-5.

[11] 常来山, 张瑞鹏, 陶东海,等. 弓长岭露天矿顺倾断层影响边坡可靠性分析[J]. 有色金属(矿山部分), 2013, 65(3):62-65.

[12] 王 东, 王 珍, 曹兰柱,等. 断层位置对露天矿顺倾层状边坡稳定性的影响研究[J]. 中国安全科学学报, 2014, 24(12):83-89.

[13] 文世鹏, 李德同. 储层构造裂缝数值模拟技术[J]. 中国石油大学学报(自然科学版), 1996,(5):17-24.

[14] 欧阳秀兰, 占文锋. 断层模拟中FLAC模拟方法的对比研究[J]. 北京工业职业技术学院学报, 2006, 5(4):77-81.

Influence of Mechanical and Geometric Parameters ofFaults on Rock Slope Stability

HE Da-zhao, HU Bin, YAO Wen-min, LI Hua-zhou, MAO Yuan-jing

(Faculty of Engineering, China University of Geosciences, Wuhan 430074, China)

The influences of strength parameters (including Poisson’s ratio, tensile strength, cohesion, and internal friction angle) and geometrical parameters (fault throw, thickness, dips, and distance from free face) of fault fracture zone on the failure mode and stability of rock slope were analyzed by FLAC3Dstrength reduction method in comparison with limit equilibrium method in Slide. Simulation results indicate that the increase of cohesion could improve the slope stability while Poisson’s ratio and tensile strength have barely no influence on the stability; the effects of internal friction angle on slope stability obtained from the two methods are different; in addition, the geometric parameters of rock-soil body in faults have a stronger impact on the failure modes and stability of rock slope than mechanical parameters do.

rock slope; faults; mechanical parameters; geometric parameters; failure mode; slope stability

2016-09-19；

2016-12-25

国家自然科学基金项目(41672317)

和大钊(1991-)，男，山东新泰人，硕士研究生，主要从事边坡稳定性分析与岩土数值模拟方面的研究。E-mail:1049510874@qq.com

胡 斌(1974-),男，山东曲阜人，教授，博士，主要从事边坡稳定性分析与数值模拟方面的研究。E-mail:40275083@qq.com

10.11988/ckyyb.20160974

TU457

A

1001-5485(2018)01-0128-05

(编辑：赵卫兵)