基于全过程曲线循环加卸载的岩石塑性硬化软化模型研究

， ，，， ，，

(1.新华水力发电有限公司，北京 100070；2. 长江科学院 水利部岩土力学与工程重点实验室，武汉 430010)

基于全过程曲线循环加卸载的岩石塑性硬化软化模型研究

张振杰1，汪斌2，朱杰兵2，冯志军1，卢波2，张利洁2，蒋昱州2

(1.新华水力发电有限公司，北京 100070；2. 长江科学院 水利部岩土力学与工程重点实验室，武汉 430010)

基于不同围压下的岩石三轴全过程循环加卸载试验成果曲线，分离出空间塑性主应变，在屈服函数上增加塑性理论中的某种塑性硬化或软化函数项，研究满足Mohr-Coulomb屈服准则的强度参数在初始屈服、峰前硬化及峰后软化全过程中随塑性参量的动态演化规律。通过试验数据整理分析，发现岩石破坏过程中在塑性硬化阶段内摩擦角、剪胀角有一个先增加后跌落的过程，而黏聚力在塑性硬化和软化阶段均减小这一规律；并采用非线性函数对该规律进行拟合回归，得到了内摩擦角、剪胀角和黏聚力等强度参数以塑性参量为函数变量的演化模型；将该规律应用于拉格朗日数值分析中，模拟了室内大理岩试件破坏过程中的应力-应变关系曲线特征。研究表明，基于岩石全过程循环加卸载试验的力学模型能较好地描述大理岩的塑性硬化塑性软化的力学行为，具有一定的理论意义和工程应用价值。

循环加卸载；塑性硬化软化；塑性参量；Mohr-Coulomb屈服准则；强度参数

1 研究背景

岩石在加载受力破坏过程中一般都会经历一段塑性硬化和软化阶段，在达到初始屈服强度后还有一个强度继续升高的过程，称作强化阶段；当岩石的应力达到峰值强度之后，随着变形继续增加，岩石强度会发生一定的劣化或跌落，称作软化阶段。由于岩石介质的复杂性，硬化和软化在物理机制上也是不同的。有学者借用经典弹塑性本构理论中的初始屈服、后继屈服(即硬化)和破坏后区的概念来描述这些进入塑性后的状态[1-2]。采用中间变量的方法将要求的量与已知的量用中间变量联系起来，建立能反映岩石非线性力学响应的本构关系为目前研究峰后应变软化的主流方法。但研究成果主要集中在应变软化方面[3-6]，这些成果多采取先验性的一些屈服函数中材料参数演化模型进行峰后软化的计算和模拟。FLAC3D中包含了应变硬化软化本构模型，该模型通过不断调整强度参数来实现对峰后的模拟，但未见用于峰前硬化阶段的模拟[7]。关于峰前应变硬化阶段的研究多集中在硬化参量的选取与函数描述方面，其研究成果相对较少，如李小春等[8]为了定量描述煤岩的塑性硬化特性，提出了根据硬化参量的几何意义进行计算的方法；白冰等[9]提出了利用虚拟强度参数来描述介质塑性硬化规律的方法，其实质也是采用了硬化阶段实际不存在的强度参数c,φ随塑性参量变化而调整这一思路。在岩土本构研究方面，应变硬化软化理论是描述岩土介质真实破坏过程的理论，成为岩土塑性理论中的重要组成部分。总之，这些研究均未将应变硬化和软化阶段放在一起来考虑研究岩石应力-应变全过程破坏曲线。

目前关于硬化软化的本构模型多简化采用三折线软化规律，这一方法与实际岩石表现的本构关系相去甚远。FLAC3D中允许用户可以自定义这些材料参数为塑性应变的函数，但未能给出如何得到强度参数与塑性参量的关系表。针对这一技术难题，本文通过大量的室内岩石三轴试验，在硬化和软化阶段的多次循环往复加卸载试验中得到材料黏聚力、内摩擦角、剪胀角等材料属性参数与塑性参量的函数关系，从而可以描述真实的岩石硬化和软化过程；最后通过内嵌到FLAC3D中采用数值模拟方法来研究岩体试件应力-应变全过程曲线中的塑性硬化软化特性及其演化过程。

2 应变硬化软化特性的试验方法

2.1 岩石峰值三轴强度参数试验

以大理岩为研究对象，将现场钻孔取芯试件密封保存托运至长江科学院岩基研究所试验室加工成长106 mm，直径53 mm的试件。试验加载系统采用MTS815刚性伺服机(见图1)，该系统最大出力量值轴向载荷4 700 kN，围压140 MPa，渗透水压140 MPa；而且具有足够的刚度保证岩石试件峰后卸荷过程中机架不对试件释放弹性能。由于系统具有多种控制通道，整个加载试验采用了侧向变形控制，对于脆性材料也具有一定的可控性;另外，在硬脆性岩石峰值附近的加卸载辅助AE声发射监测，保证了不会发生峰后脆性失稳式破坏。

图1 MTS815.03岩石力学试验系统Fig.1 The MTS815.03 rock mechanical test system

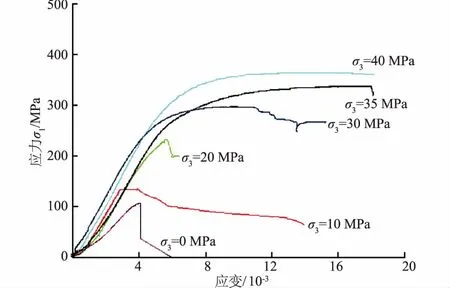
图2 三轴试验全过程曲线σ-ε关系曲线Fig.2 Triaxial σ-ε curves of marble test

塑性应变演化过程的三轴循环加、卸载试验之前，首先进行室内常规单轴和三轴试验，试验曲线成果见图2所示，得到该组岩样的单轴抗压强度约80.0 MPa，平均变形模量为35.8 GPa，弹性模量50.6 GPa，泊松比0.24。根据三轴摩尔-库伦强度准则得到髙围压下岩样三轴压缩抗剪强度参数为：内摩擦角45°,黏聚力16 MPa。

2.2 损伤控制的AE辅助试验方法

为求出三轴试验过程中任意一屈服应力下的塑性主应变，可采用该点处加卸载试验方法分离出不可逆的塑性应变。该方法在其他文献中也有报道，但多未卸载至应变轴上，而采用卸荷过程中所有的弹性模量恒定这一假设(含峰前峰后)，这与实际情况不符。

实际应用中，对于硬脆岩石采用损伤控制的循环加卸载方法，尤其是在单轴或低围压条件下加载至峰值强度附近时，尽管现在伺服机的加载机架刚性已足够大，但恰好越过峰值点后的软化段加卸载点很难控制，即使采用应变控制模式，实际操作中也很难保证岩样峰后平稳破坏。根据发明专利技术“岩石三轴单样法多级屈服点的声学判别方法及装置”，采用AE声发射和体应变曲线实时监测显示同时综合判断，解决了脆性岩石在峰值强度附近区域屈服点难以控制和判别的关键技术难题，从而可以实现全过程损伤控制的循环往复加卸载试验。如图3所示，岩石微裂隙扩展过程控制可以借助声发射装置安装高频声发射AE探头进行实时监控；图4为三轴条件下大理岩损伤控制的全过程加卸载破坏试验中采集到的AE声发射率和能率信号。从图4中可以辨识出初始屈服—后继屈服段声发射数和能量释放速率的变化特征，为试验的人工干预控制提供了判断依据。

图3 三轴循环加卸载中的三轴AE声发射装置Fig.3 The AE monitor and triaxial cell

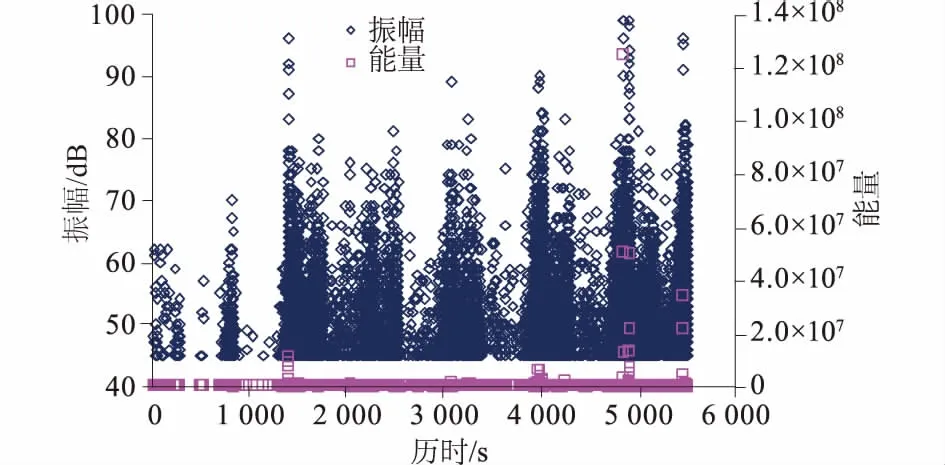
图4 损伤控制加卸载试验中的AE声发射监测成果Fig.4 AE monitoring results in the whole process of damage controlling test under varying σ3

2.3 岩石三轴循环加卸载试验成果曲线

采用以上试验方法和方案，得到了大理岩全过程破坏中的不同屈服应力点对应的轴向、侧向塑性应变之间的关系曲线(如图5所示)，进而可以得到全过程曲线任意轴向应力对应的主塑性应变。

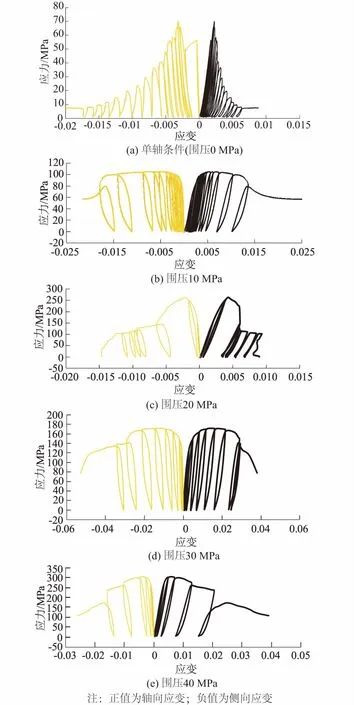
图5 不同围压下加卸载全过程曲线Fig.5 The loading and unloading curves of triaxial testing under different confining pressures

由给出的0，10，20，30，40 MPa条件下三轴加卸载全过程曲线，可以得到如下几点特征。

(1) 加卸载曲线遍及了首次屈服前、塑性硬化以及峰后软化3个阶段，每次加载和卸载在应变坐标轴上并不重合，而是由于每次加卸载循环中产生了不可逆塑性变形从而形成一系列的闭合环；而且随着塑性变形的累积，闭合环的形态由细长变为短粗形态，其闭合面积(耗散的塑性功)也由小变大。

(2) 比较不同围压下的加卸载全过程曲线，可看出单轴状态下加卸载过程中消耗的塑性功相对高围压下要小，峰后塑性阶段相对较短，整体曲线表现为脆弹塑性破坏；高围压下峰后塑性及延性表现强烈，峰后的残余强度也随围压的增加而增加，对应的累计塑性变形也大些，与常规三轴曲线表现出相同规律。

3 强度参数演化模型及方法

3.1 硬化软化参量的选取与实现

我们知道在弹塑性力学中，应力不仅与应变有关，还与整个变形历史有关，即具有历史相关性(或路径相关性)。要描述弹塑性介质的状态，除了需要应力、应变等外状态变量外，还需要一组合适的内状态变量κ，也可称为塑性参量，κ可取为塑性剪应变、塑性功、塑性体应变或等效塑性应变等。为了更好地刻画描述图5整个试验过程中的塑性应变历史累积和演化过程，就必须选择一个能标识和记录塑性变形历史的塑性特征演化参量，而且要与应力路径无关。在数学上，塑性参量通过塑性硬化或软化函数提供了一个对塑性定量描述的参数。该处我们选择与FLAC3D中相同定义的塑性参量εp。FLAC3D中应变软化模型在数值计算中采用的软化参数是等效塑性剪切应变εp，其增量形式定义为

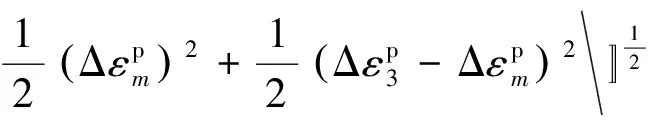
(1)

其中,

(2)

3.2 内摩擦角和黏聚力演化模型

在软化模型中，一般采用用户自定义黏聚力、内摩擦角、剪胀角等变量可以写成总应变中塑性参量εp的函数。为此，基于以上大理岩的全过程加、卸载三轴试验研究成果，可以得到任意塑性参量εp下不同围压下偏应力(σ1-σ3)与塑性参量εp的曲线簇，如图6所示。

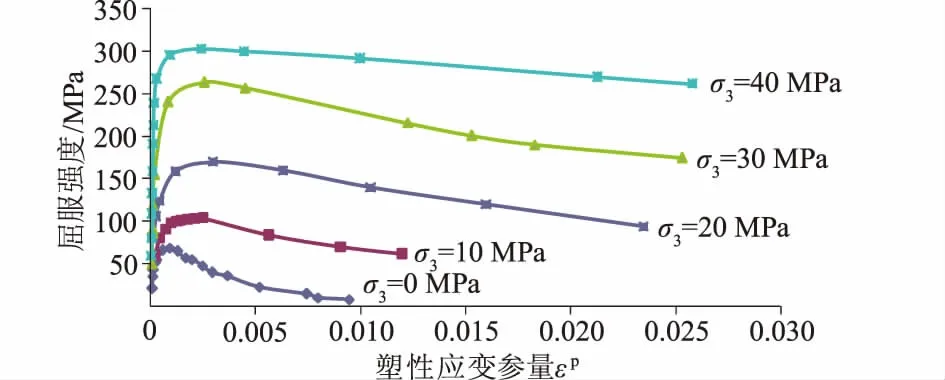
图6 不同塑性参量下对应的三轴屈服应力曲线簇Fig.6 Curves of yield stress vs. plastic parameter under different confining stresses

由这些曲线可得出不同围压条件下对应的屈服应力值，将各条曲线上具有相同塑性参量εp的应力点连接起来，认为这些点处于相同的硬化或软化面上。对于不同的εp值可拟合出不同的后继屈服面，在满足初始和后继屈服满足Mohr-Coulomb准则条件下，最后得到的屈服面形式为

f(σ1,σ3,εp)=σ1-m(εp)σ3-b(εp) 。

(3)

式中:σ1，σ3分别为最大、最小主应力；屈服准则函数待定系数m和b均为等效塑性剪切应变εp的函数,即：

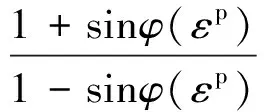
(4)

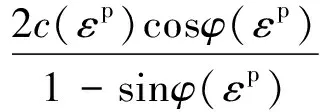
(5)

由式(4)、式(5)可以回归得到硬化面或后继屈服面上的强度参数黏聚力c和内摩擦角φ随塑性参量的演化函数关系曲线(见图7)。

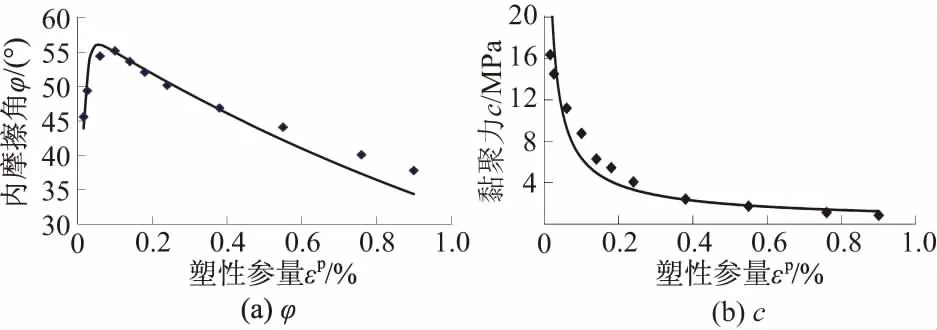
图7 基于摩尔-库伦准则回归的φ和c随塑性参量演化曲线Fig.7 Curves of φ and c vs. plastic parameter based on Mohr-Coulomb criterion

由图7可知，岩石破坏过程中在塑性硬化阶段内摩擦角有一个先增加然后跌落的过程，而黏聚力在塑性硬化和软化阶段均一直降低。这一规律为后续数值试验分析提供了通过室内试验得到的应变硬化软化本构关系。

采用指数函数的组合形式来描述内摩擦角的变化规律，函数取式(6)所示形式；对于黏聚力变化曲线采用幂函数形式，如式(7)所示。其中两函数的待定系数分别为P1,P2,P3,P4。回归后的内摩擦角和黏聚力模型参数见表1，其拟合曲线见图7所示。

φ=P1P2[exp(-P2εp)-

exp(-P1εp)]/(P1+P2) ；

(6)

(7)

3.3 剪胀角演化模型

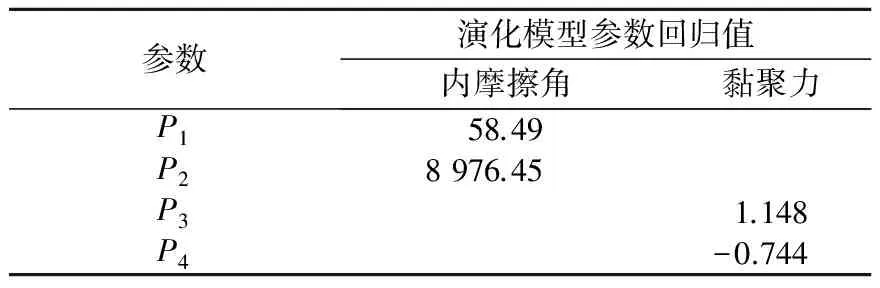
表1 内摩擦角和黏聚力演化模型参数回归值Table 1 Regression values of internal frictional anglemodel under different confining pressures

剪胀角ψ作为材料参数来描述扩容物质的性质，如式(8)所示，其表征参数Kψ含义就是塑性体积变形率与塑性剪切变形率的比值，经过换算推导可以写成式(9)。国内学者多采用“每次加卸载过程中岩石保持变形的变形模量始终恒定”这一假定，采用三轴一次压缩破坏曲线进行塑性应变分离，显然峰前峰后岩石变形特性差异巨大，不切实际[10-11]。 Alejano等[11]给出了岩石荷载下裂纹稳定发展初始至加速发生直至残余强度之间的侧向塑性主应变-塑性轴向主应变关系曲线的分离方法。本文采用损伤控制的三轴全过程循环往复加卸载试验方法更为合理。因此，根据图5中各围压下的系列滞回圈，可以得到系列曲线上的塑性主应变和弹性主应变。根据式(9)和拟合函数式(10)得到剪胀角随塑性参量变化的回归曲线，由于篇幅原因，此处仅给出单轴和10 MPa围压下的拟合曲线(见图8)。剪胀角回归模型参数P5和P6见表2。

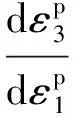
(8)

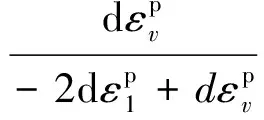
(9)

ψ=P5P6[exp(-P6εp)-

exp(-P5εp)]/(P5+P6) 。

(10)

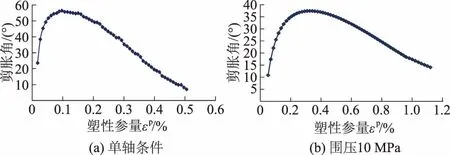
图8 单轴和10 MPa围压下岩石剪胀角随塑性参量演化回归曲线Fig.8 Regression curves of dilatancy angle vs. plastic parameter under uniaxial condition and10 MPa confining pressure

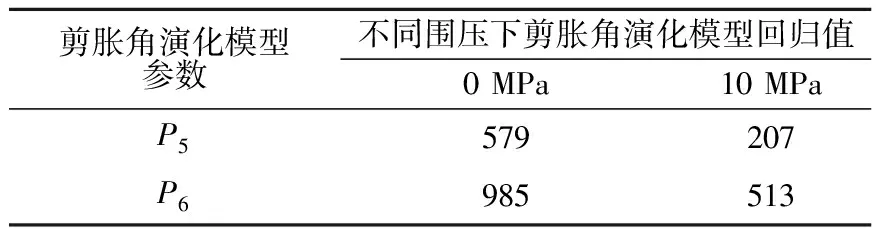
表2 不同围压下双参数剪胀角模型参数回归值Table 2 Regression values of dilatancy angle modelunder different confining pressures

4 应变硬化软化的数值验证分析

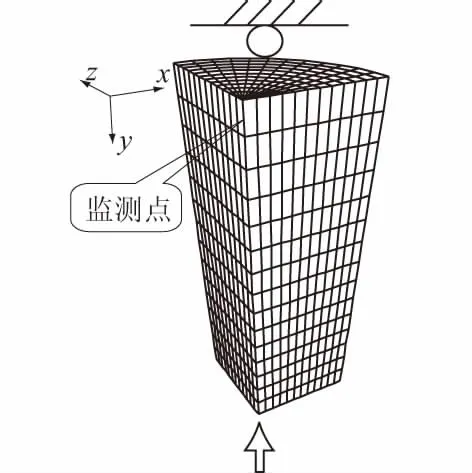
图9 岩样数值试验的计算单元及边界条件Fig.9 Elements and boundary condition of numerical model

FLAC数值试验的模型几何尺寸参照岩石试验规程，设计为Φ53 mm×106 mm圆柱体，单元划分及边界加载条件见图9。在试样的上端面施加固定铰支座约束，在试样的下端面施加常位移速度为2×10-6m/s，模型侧向采用应力控制模拟围压，其他参数采用前文中试验参数。岩石材料的满足取摩尔-库伦剪破坏与拉破坏复合的屈服准则，本构关系采用应变软化模型来研究应力变形性能，对于峰前硬化和峰后软化采用图7所示的函数对应关系式(6)、式(7)对强度参数进行调整。

图10给出了计算得到的岩石应力-应变曲线与试验曲线(该处仅列出单轴和围压10 MPa条件下曲线)。对于单轴和三轴应力-应变曲线，峰前硬化阶段和峰后软化阶段均有一定的差异，但数值计算曲线也表现出一定的应变硬化和应变软化效应。就整体而言，基于试验成果的数值计算结果与试验曲线基本吻合，说明该模型能描述大理岩的应变硬化和软化力学行为。

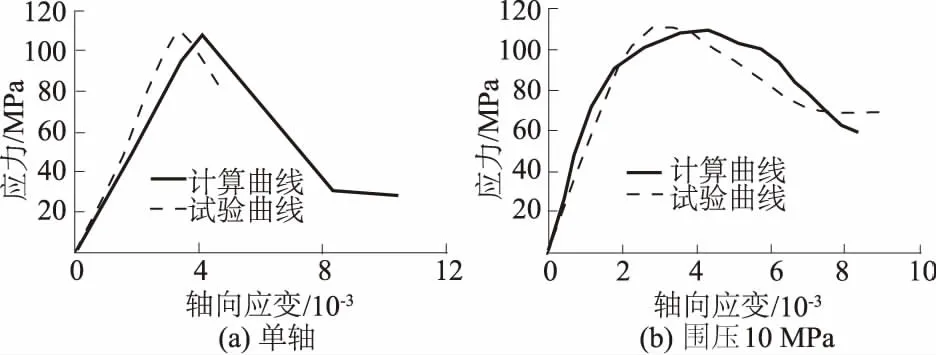
图10 基于应变软化模型的应力-应变曲线Fig.10 Curves of stress-strain based on strain softening constitutive model

5 结 论

本文通过室内三轴加卸载控制的试验方法来研究大理岩应力-应变曲线的塑性硬化和软化特性，得到以下几点结论。

(1) 文中给出的基于MTS815系统的侧向应变式损伤控制的全过程曲线加卸载三轴试验方法解决了FLAC3D中未能给出的关于岩土类材料参数如内摩擦角、黏聚力和剪胀角等随塑性参数函数变化关系的获取方法等技术难题。

(2) 在屈服函数上增加塑性理论中的某种塑性硬化或软化函数项，得到了满足Mohr-Coulomb准则的强度参数在初始屈服及峰前硬化、峰后软化过程中随塑性参量的动态演化规律，即岩石破坏过程中在塑性硬化阶段内摩擦角和剪胀角有一个先增加然后跌落的过程，而黏聚力在塑性硬化和软化阶段均减小。

(3) 通过函数拟合及回归方法，建立了岩石破坏过程中内摩擦角、黏聚力和剪胀角随塑性参量变化的演化模型及其参数；通过数值计算分析与试验曲线对比，结果表明基于室内循环加卸载损伤控制试验方法所建立的应变硬化软化本构关系能合理地描述大理岩的塑性硬化和塑性软化的力学行为，具有一定的理论意义和应用价值。

[1] 郑颖人，沈珠江，龚晓南．岩土塑性力学原理[M]．北京：中国建筑工业出版社，2002.

[2] 王 仁. 塑性力学基础[M]. 北京：科学出版社，1998.

[3] 李文婷，李树忱，冯现大，等. 基于莫尔-库仑准则的岩石峰后应变软化力学行为研究[J]. 岩石力学与工程学报，2011，30(7)：1460-1466.

[4] 王水林，王 威，吴振君. 岩土材料峰值后区强度参数演化与应力-应变曲线关系研究[J]. 岩石力学与工程学报，2010，29(8)：1524-1529.

[5] 姚再兴. 软化Drucker-Prager 材料强度参数的测定方法[J].岩石力学与工程学报，2014，33(6)：1187-1193.

[6] Itasca Consulting Group Inc.. FLAC3D(Version 2.1) Users Manual[R]. USA: Itasca Consulting Group Inc., 2003.

[7] 陆银龙，王连国，杨 峰，等. 软弱岩石峰后应变软化力学特性研究[J]. 岩石力学与工程学报，2010，29(3)：641-648.

[8] 李小春,白 冰,唐礼忠，等. 较低和较高围压下煤岩三轴试验及其塑性特征新表述[J]. 岩土力学, 2010, 31(3):677-682.

[9] 白 冰,李小春,石 露,等. 基于虚强度参数的塑性硬化模式[J].长江科学院院报，2012, 29(8):24-28.

[10] MEDHURST T P, BROWN E T. A Study of the Mechanical Behavior of Coal for Pillar Design[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1998, 35(8):1087-1105.

[11] ALEJANO L R，ALONSO E. Considerations of the Dilatancy Angle in Rocks and Rock Masses[J]. International Journal of Rock Mechanics and Mining Sciences,2005, 42(4): 481-507.

Plastic Hardening and Softening Model of Rock Based on CyclicLoading and Unloading Testing Throughout Failure Process

ZHANG Zhen-jie1，WANG Bin2, ZHU Jie-bing2， FENG Zhi-jun1, LU Bo2，ZHANG Li-jie2，JIANG Yu-zhou2

(1.Xinhua Hydropower Company Limited, Beijing 100070, China; 2.Key Laboratory of Geotechnical Mechanics and Engineering of Ministry of Water Resources, Yangtze River Scientific Research Institute, Wuhan 430010, China)

According to curves acquired from cyclic triaxial loading-unloading tests on marble, the spatial plastic principal strains are obtained, and some plastic hardening and softening functions in classic plastic theory are embedded into the current yielding function. On this basis, the dynamic evolutionary process of strength parameters which meet Mohr-Coulomb criterion against the variation of plastic parameter throughout the process of initial yielding, pre-peak hardening and post-peak softening is researched. Processing and analysis of test data revealed that internal friction angle and dilatancy angle witnessed an increase at first and then a decline in plastic hardening period; whereas cohesion decreased both during hardening and softening. Furthermore, through nonlinear function fitting, the models of strength parameters (internal friction angle, dilatancy angle and cohesion) varying with plastic parameters are obtained. The stress-strain relationship of marble in in-door test was simulated by applying the models into FLAC3Dprogram. Research results show that the constitutive relation derived from triaxial loading and unloading control testing could reasonably describe the characteristic of plastic hardening and softening mechanical behavior, and therefore is of theoretical significance and application value.

cyclic loading and unloading; plastic hardening and softening; plastic parameter; Mohr-Coulomb yield criterion; strength parameters

2017-04-19；

2017-07-06

新华水电科研课题项目(新华2016-A65)；国家重点研发计划专项(2016YFC0401801)；国家自然科学基金项目(41672320,51579017)

张振杰(1963-)，男，山西夏县人，教授级高级工程师，硕士，主要从事水利水电工程建设与科研管理等方面的研究工作。E-mail: zzj02156@vip.sina.com

朱杰兵(1970-)，男，安徽怀宁人，教授级高级工程师，博士，主要从事岩石力学基本特性和岩土安全监测技术方面的研究工作。E-mail:zhujb@vip.163.com

10.11988/ckyyb.20170430

TU452

A

1001-5485(2018)01-0095-06

(编辑：陈 敏)