基于组合模型的铁路客运量预测

胡小敏， 贺园园

(西安交通工程学院，西安 710300)

基于组合模型的铁路客运量预测

胡小敏， 贺园园

(西安交通工程学院，西安 710300)

为了提高铁路客运量的预测精度，针对单一铁路客运量预测模型以及传统组合预测模型的缺陷，设计了基于组合模型(ARIMA-LSSVM)的铁路客运量预测方法，采用ARIMA对铁路客运量的周期性变化特点进行建模预测，从整体上把握铁路客运量的变化特点，采用LSSVM对铁路客运量的随机性变化特点进行预测，采用具体铁路客运量预测实例对性能进行测试和分析。结果表明，ARIMA-LSSVM可以准确、全面描述铁路客运量的变化特点，提高了铁路客运量的预测准确性，预测结果可以为铁路管理者提供有价值信息。

铁路客运量； 组合预测模型； 最小二乘支持向量机； 自回归移动平均模型

0 引言

随着我国交通事业的不断发展，铁路客运量不断增加，铁路客运量预测结果可以指导铁路企业和管理进制定相应的措施，对于提高经营、管理水平具有重要的意义[1]。铁路客运量受到许多因素影响，如经济、政策、人口数量等，这些因素之间又相互影响，导致铁路客运量变化十分复杂，设计性能优异的铁路客运量预测模型成为了铁路研究领域的一个重要方向[2]。

铁路客运量具有随机性、周期性变化特点，而且非平稳性相当明显，难以建立精确的数学模型[3]，当前常根据铁路客运量的历史数据进行建模，历史数据隐藏一定变化特征，可以从中发现铁路客运量的变化规律[4]。当前铁路客运量预测模型主要分为两类：线性模型和非线性模型[5]，线性模型主要有：时间序列方法、回归分析法[6,7]，它们认为铁路客运量是一种线性的变化趋势，待确定参数少，易实现，建模效率高，但铁路客运量不简单是一种线性变化趋趋势，同时还具有非线性变化趋势，因此线性模型的铁路客运量预测精度低，预测结果的可信度低，在实际应用中的范围受限[8]。非线性模型主要有神经网络和支持向量机[9,10]，可以对铁路客运量的非线性变化特点进行建模，但无法对铁路客运量的线性变化特点进行预测，因此预测结果也不太可靠。针对单一模型存在的不足，有学者提出了基于组合模型的铁路客运量预测方法[11,2]，如灰色模型和线性回归、线性回归和马尔可夫模型之间的组合，不同模型可以提供更多的铁路客运量的信息，提高了铁路客运量的预测效果，但组合模型到底如何进行组合，当前没有统一理论指导，铁路客运量的预测结果有待进一步改善。

自回归移动平均模型(ARIMA)模型融合了时间序列分析和回归分析的优点，但无法描述非线性数据的信息，最小二乘支持向量机(LSSVM)具有良好的非线性拟合能力，针对铁路客运量的线性和非线性变化特点，提出基于ARIMA-LSSVM的铁路客运量组合预测模型，并通过具体实验验证ARIMA-LSSVM的有效性和可行性。

2 ARIMA和LSSVM

2.1 ARIMA

ARIMA模型是差分运算和ARMA模型的结合，对于含有非季节性的时间序列进行建模，可使用ARIMA(p,d,q)模型，可以通过适当的d阶差分运算使序列平稳，一般形式为式(1)。

(1)

式中：{yt}为平稳时间序列；{εt}为白噪声序列：φi,θj(i=1,2,…,p；j=1,2,…,q)分别是{yt}、{εt}的参数；p为自回归阶数，q为移动平均阶数。

2.2 LSSVM

对于训练样本集{(xi,yi)},i=1,2,…n，xi∈Rn,yi∈R，xi和yi分别表示样本输入和输出，通过非线性映射函数φ(·)将样本映射到高维特征空间，在高维特征空间进行线性回归，如式(2)。

f(x)=wTφ(x)+b

(2)

式中，ω为权值向量，b为偏置量。

根据结构风险最小化原则，式(2)问题求解可以变为式(3)。

s.t.yi-wTφ(x)+b=ei

(3)

式中，γ为正规则化参数；ei为实际值与回归结果的误差。

通过引入拉格朗日乘子将上述约束优化问题转变对偶空间优化问题，得到式(4)。

(4)

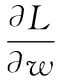
wφ(xi)+b+ξi-yi=0

(5)

根据Mercer条件，核函数定义K(xi,xj)=φ(xi)Tφ(xj)，LSSVM回归模型为式(6)。

(6)

选择RBF函数作为LSSVM核函数，其定义为式(7)。

(7)

式中，σ为宽度参娄。

最后LSSVM回归模型为式(8)。

(8)

3 ARIMA-LSSVM的铁路客运量预测模型

铁路客运量受到多种因素影响，具有随机性、非平稳性、周期性等变化特点，单一ARIMA或者LSSVM无法建立高精度的铁路客运量预测模型。针对ARIMA和LSSVM的缺陷，结合它们线性和非线性预测优点，将它们组合在一起应用于铁路客运量预测中。ARIMA-LSSVM的铁路客运量预测原理为：采用ARIMA对铁路客运量进行建模，描述铁路客运量的周期性变化特点，然后LSSVM对铁路客运量进行建模，反映铁路客运量的随机性变化特点，最后通过神经网络确定两者权值，对它们结果进行加权组合得到铁路客运量的最终测结果，工作流程如图1所示。

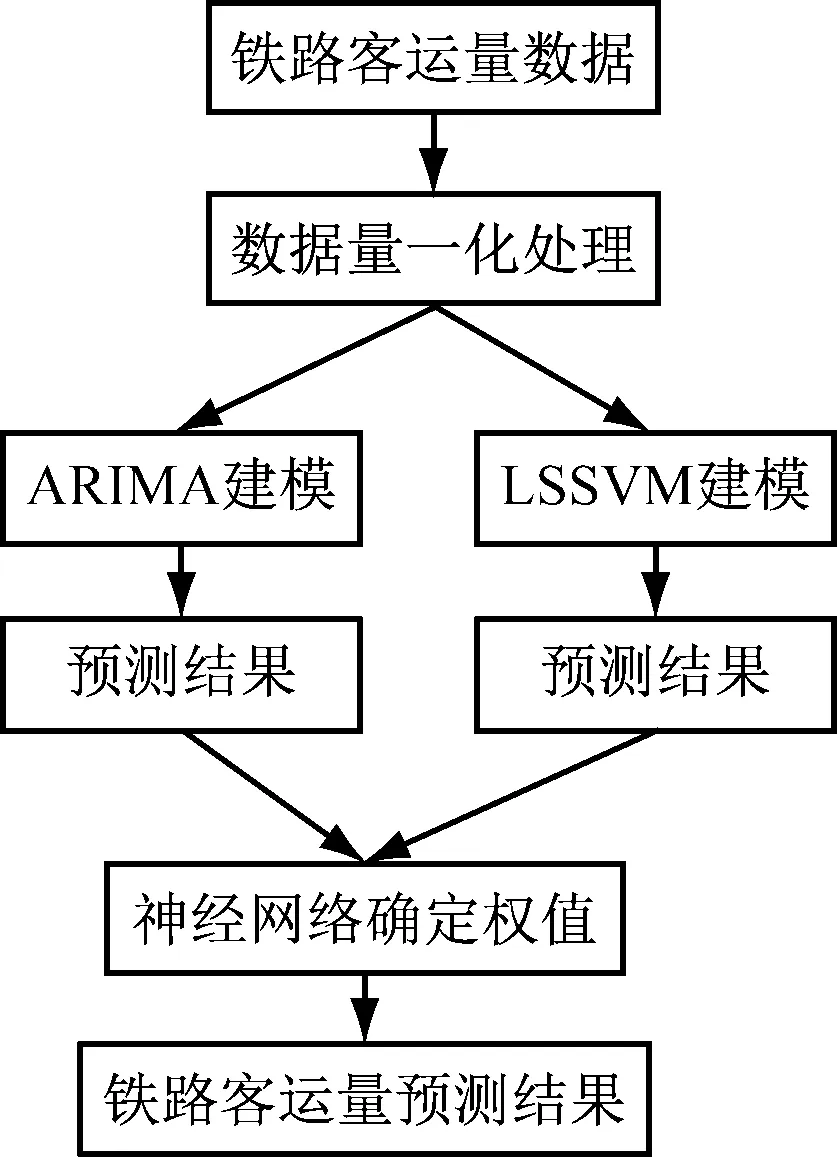
图1 ARIMA-SVM的铁路客运量预测流程

4 仿真实验

4.1 数据来源

为了测试ARIMA-LSSVM铁路客运量预测模型的性能，选择1985～2016年的全国铁路客运量数据作为实验对象，选择后20个数据作为测试样本，其它数据作为训练样本，如图2所示。

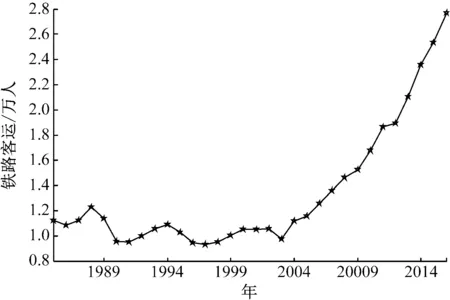
图2 铁路客运量数据

从图2可知，铁路客运量数据变化范围大，对铁路客运量建模产生不利影响，为此将其归一化到[0 1]区间，具体为式(9)。

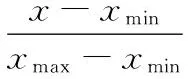
(9)

式中，x为原始数据，xmax和xmin为最大和最小的铁路客运量[14]。

4.2 ARIMA的铁路客运量预测

4.2.1 ARIMA模型参数估计

铁路客运量的原始自相关函数(ACF)和偏相关函数(PACF)如图3所示，从图3可以发现，铁路客运量数据之间的相关性很高，需要进行差分处理。1阶差分的ACF和PACF,如图4所示。

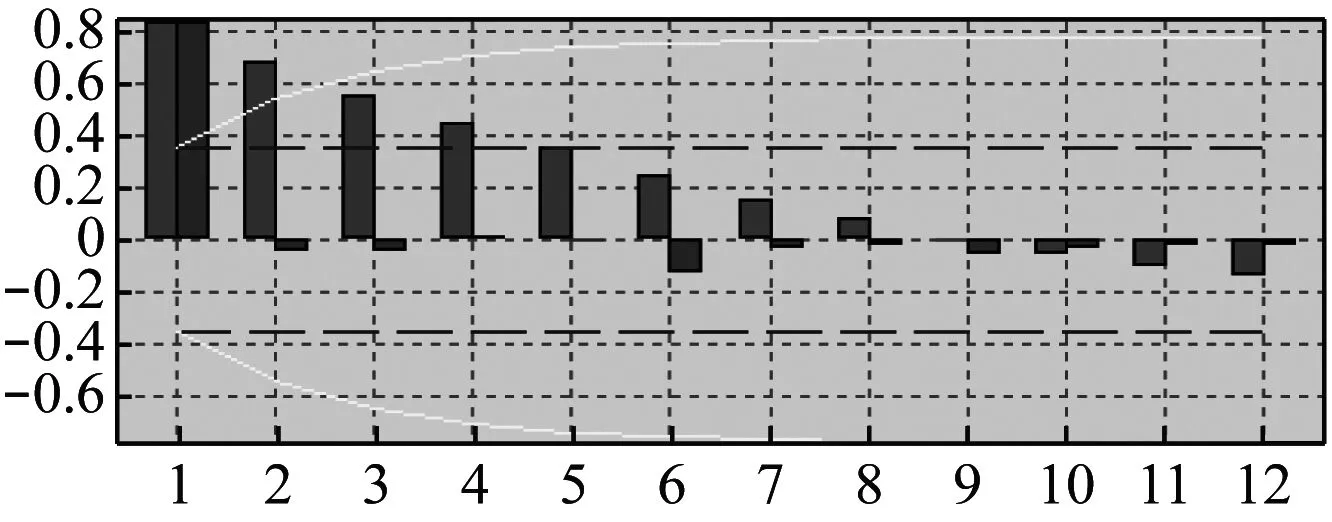
图3 铁路客运量的原始ACF和PACF

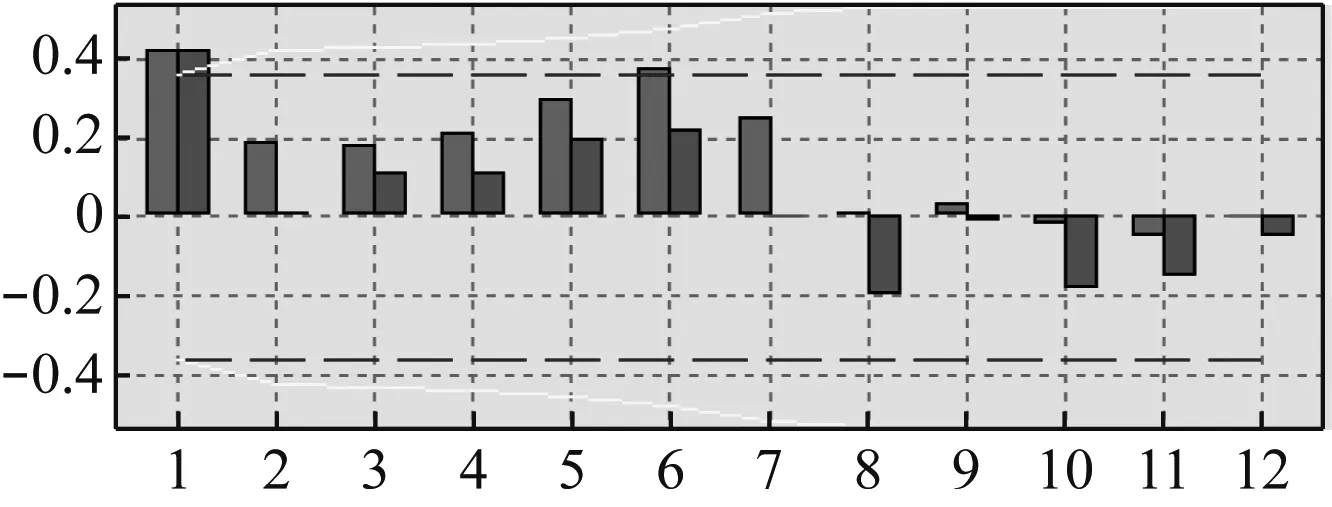
图4 1阶差分后ACF和PACF

1阶差分后，铁路客运量数比较平稳，即ARIMA的参数d=1，最终确定铁路客运量的ARIMA(3,1,2)。

4.2.2 ARIMA的铁路客运量预测结果

采用ARIMA(3,1,2)对铁路客运量的训练样本进行建模，并对测试样本进行预测，铁路客运量的预测结果,如图5所示。

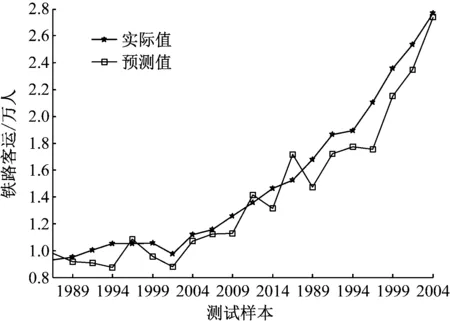
图5 ARIMA的铁路客运量预测结果

从图5可以看出，ARIMA可以整上对铁路客运量的变化趋势进行描述，但预测偏差比较大，铁路客运量的有待进一步改善。

4.3 LSSVM对铁路客运量进行预测

采用LSSVM对铁路客运量的训练样本进行建模，并对测试样本进行预测，铁路客运量的预测结果如图6所示。

从图6可以看出，LSSVM的预测结果比ARIMA要好，但仍然多个样本点的预测偏大，预测结果不稳定，这主要是由于LSSVM只能提供铁路客运量部分信息，铁路客运量精度有待提高。

4.4 ARIMA-LSSVM的铁路客运量预测结果

采用BP神经网络确定ARIMA和LSSVM的铁路客运量预测结果的权值，融合得到铁路客运量最终预测结果如图7所示。

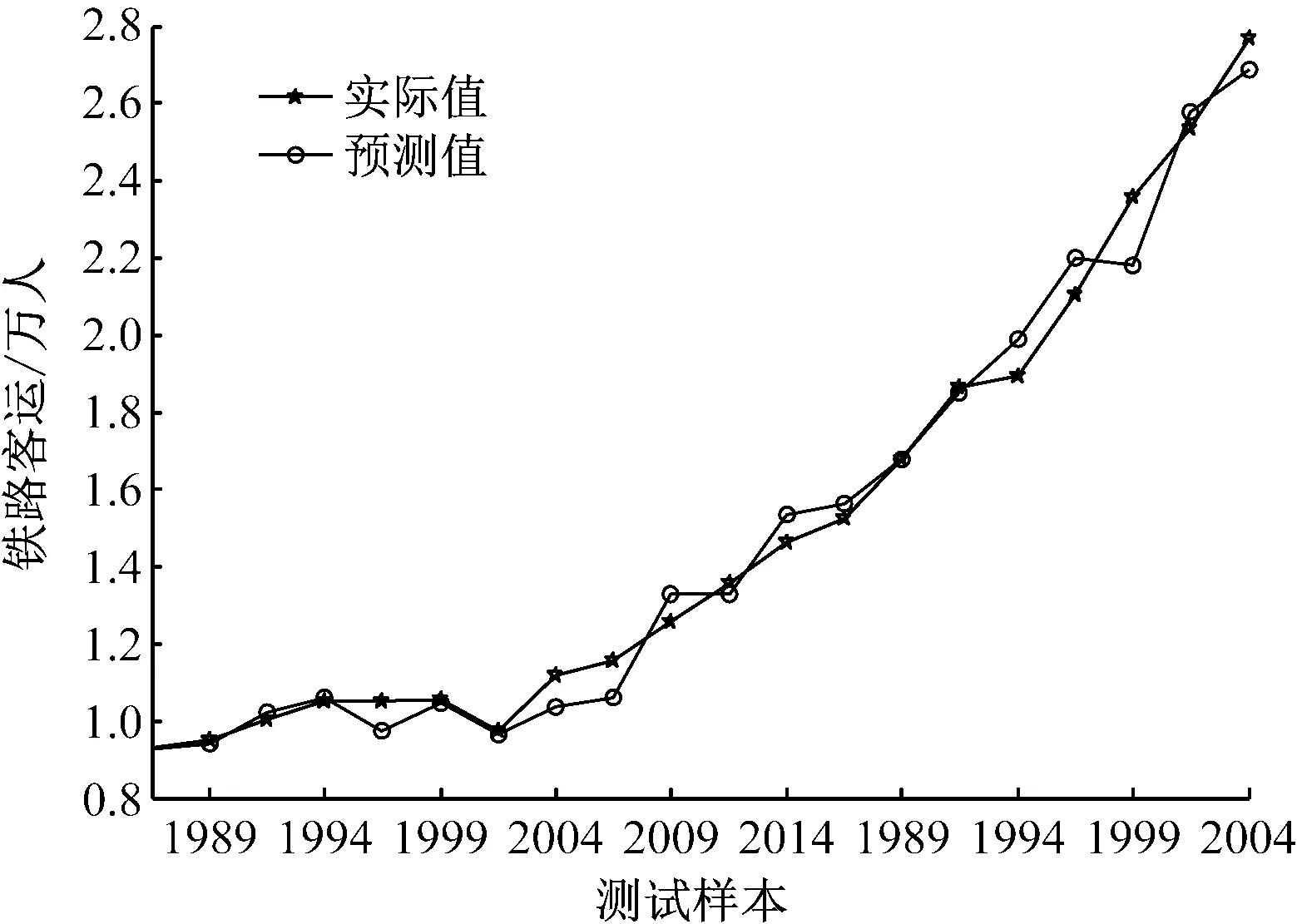
图6 LSSVM的铁路客运量预测结果

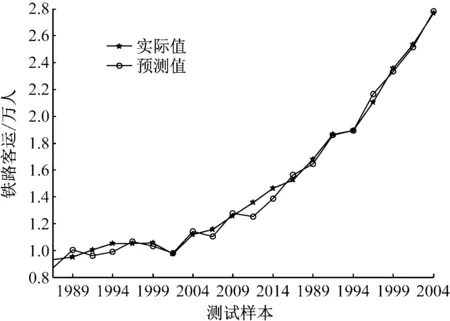
图7 ARIMA-LSSVM铁路客运量的预测结果

从图7可知，ARIMA-LSSVM铁路客运量的预测精度比ARIMA、LSSVM要高，主要是综合利用了ARIMA和LSSVM优势，更加准确描述铁路客运量变化趋势，改善了铁路客运量预测效果。

5 总结

为了提高铁路客运量的预测精度，针对单一模型无法全面描述铁路客运量变化特点的缺陷，提出了基于ARIMA-LSSVM的铁路客运量预测方法，并采用具体铁路客运量预测实例对模型的性能进行测试和分析，结果表明，ARIMA-LSSVM通过ARIMA对铁路客运量的周期性变化特点进行建模预测，可以从整体上把握铁路客运量的变化特点，采用LSSVM对铁路客运量的随机性变化特点进行预测，提高了铁路客运量的预测准确性，预测结果有助于对铁路管理者制定相应的措施。

[1] 黄召杰,冯硕. 灰色预测模型在铁路客流预测中的应用[J]. 交通科技与经济,2014,16(1): 57-60.

[2] 蔡昌俊,姚思建,王梅英,等. 基于乘积 ARIMA 模型的城市轨道交通进出站客流量预测[J]. 北京交通大学学报,2014,38(2): 135-140.

[3] 王文莉,杨俊红. 基于灰色理论的铁路客运量预测影响因素优化[J]. 微电子学与计算机, 2011, 28(10): 164-167.

[4] 彭珍瑞,孟建军,祝磊,等 . 基于支持向量机的铁路客运量预测[J].辽宁工程技术大学学报:自然科学版,2007,26(2):269-272.

[5] 侯丽敏,马国峰. 基于灰色线性回归组合模型铁路客运量预测[J]. 计算机仿真,2011,28(7): 1-3.

[6] 王卓, 王艳辉, 贾利民, 等.改进的BP神经网络在铁路客运量时间序列预测中的应用[J]. 中国铁道科学, 2005, 26(2): 128～131.

[7] 孟歌,伍忠东,Muhammad Waqas Ahmad. FSVR在铁路趟车客运量预测中的应用[J]. 济南大学学报(自然科学版), 2015, 29(5): 382-388.

[8] 朱伟,李楠,石超峰. 基于粒子群算法优化支持向量机的铁路客运量预测模型[J]. 商丘师范学院学报, 2013,29(12): 33-34.

[9] 赵清艳,熊茂华. 混沌粒子群优化神经网络在铁路客运量预测中的应用[J]. 计算机应用与软件, 2013, 30(6): 225-228.

[10] 刘琳玥. 基于PCA-BP 神经网络的铁路客运量预测模型研究[J]. 综合运输,2016, 38(8): 43-48.

[11] 冯冰玉, 鲍学英, 王起才, 董朝阳. 新型组合模型在铁路客运量预测中的应用[J]. 铁道标准设计, 2015, 59(12): 6-9.

[12] 李晓东. 基于线性回归—马尔可夫模型的铁路客运量预测[J]. 铁道运输与经济,2012, 34(4): 38-41.

[13] 贺晓霞,鲍学英,王起才,董朝阳. 基于GM-周期扩展组合模型的铁路客运量预测[J]. 铁道科学与工程学报,2015, 12(3): 685-689.

[14] 褚鹏宇,刘澜. 基于变权重组合模型的铁路客运量短期预测[J]. 计算机工程与应用,2017, 53(4): 228-232.

RailwayPassengerVolumePredictionBasedonHybridModel

Hu Xiaomin, He Yuanyan

(Xi’an Traffic Engineering Institue, Xi’an 710300, China)

According to the defects of passenger traffic volume of railway single prediction model and traditional combination forecasting model, in order to improve the prediction accuracy of railway passenger volume, the combined model (ARIMA-LSSVM), a prediction method for railway passenger volume is designed. The railway passenger volume change periodic characteristics are predicted by ARIMA to grasp the whole railway passenger traffic volume, then the random variation characteristics are predicted by LSSVM for railway passenger volume forecast, at last passenger railway concrete is verified by test and analysis. The prediction results of the model show that the ARIMA-LSSVM model can accurate and comprehensive describe the railway passenger volume. The model improves the prediction accuracy of railway passenger volume, forecast results can help to provide valuable information to the railway management.

Railway passenger volume; Combined forecasting model; Least squares support vector machines; Auto regressive integrating moving average

1007-757X(2017)12-0067-04

胡小敏(1978-)，女，渭南人，硕士，讲师，研究方向：铁路客运。

贺园园(1985-)，女，西安人，硕士，讲师，主要研究方向：地理信息系统。

TP391

A

2017.08.29)