硫酸盐侵蚀下轴心受压钢筋混凝土柱应力时变过程的数值分析
2018-01-10王佳林左晓宝马强殷光吉汤玉娟
王佳林,左晓宝,马强,殷光吉,汤玉娟
(南京理工大学 土木工程系,南京 210094)

硫酸盐侵蚀下轴心受压钢筋混凝土柱应力时变过程的数值分析
王佳林,左晓宝,马强,殷光吉,汤玉娟
(南京理工大学 土木工程系,南京 210094)
针对荷载和硫酸盐耦合作用过程中钢筋混凝土柱的应力分析问题,在已有混凝土内硫酸根离子扩散反应模型的基础上,进一步给出了硫酸盐侵蚀引起的混凝土损伤程度与硫酸根离子浓度及腐蚀时间之间的关系,建立了与损伤程度相关的混凝土腐蚀本构模型及轴压混凝土柱截面应力的计算方法,并通过数值模拟分析了柱截面内硫酸根离子传输、腐蚀损伤程度变化、截面应变和应力分布规律。结果表明:硫酸根离子浓度和混凝土损伤程度在柱截面内呈梯度分布,且受二维交互效应的影响明显;随腐蚀时间的增加,截面损伤区逐渐向内移动且其宽度增加,而混凝土应力在损伤区呈先增加后逐渐降低、在未损伤区基本呈线性增加的趋势。硫酸盐侵蚀过程中,轴压混凝土柱截面应力发生了明显的重分布现象。
混凝土;硫酸盐侵蚀;轴心受压;损伤;应力重分布
长期处于滨海、地下水及盐渍土等侵蚀环境下的混凝土结构不仅承受各种荷载作用,还遭受硫酸盐等环境介质的物理化学侵蚀,导致混凝土结构的安全性和耐久性降低[1-2]。硫酸盐侵蚀过程中,环境中的硫酸根离子经扩散而进入混凝土内部,与水泥水化产物发生化学反应,导致混凝土腐蚀损伤[3],造成其弹性模量、强度等宏观力学性能降低。由于渗入的硫酸根离子浓度在混凝土内呈梯度分布[4],其内部损伤程度和力学性能发生不均匀变化。因此,荷载作用下混凝土结构或构件在硫酸盐侵蚀过程中,其截面力学性能发生不同程度的损伤退化,造成截面应力在损伤区降低、非损伤区上升,从而形成应力重分布现象,这种应力重分布规律与硫酸盐侵蚀混凝土的损伤退化过程密切相关。
硫酸盐侵蚀下混凝土损伤退化过程涉及离子传输、微结构演变及宏观性能劣化等方面。目前,基于多孔介质传输理论或Fick定律,建立了硫酸根离子在混凝土中传输的模型,获得了硫酸根离子在混凝土中的扩散反应规律[5-6];利用XRD、ESEM、EDS等微观测试方法,研究了硫酸盐侵蚀下混凝土等水泥基材料中侵蚀产物的生长特点及其微结构演变规律,揭示了硫酸盐侵蚀混凝土微结构损伤机理[7-8];通过混凝土试件在硫酸盐溶液中的腐蚀试验,开展了试件在不同腐蚀时间的力学性能测试,获得了混凝土强度、动弹性模量和泊松比等宏观力学性能参数随硫酸盐浓度、腐蚀时间的变化规律[9-11];此外,人们还开展了硫酸侵蚀后混凝土抗压实验研究,获得了不同腐蚀时间及应变速率等条件下混凝土本构模型[12-14]。上述研究主要揭示了硫酸盐侵蚀过程中混凝土的损伤劣化机理及其强度、刚度等宏观力学性能的退化规律,但对荷载和硫酸盐侵蚀耦合作用过程中混凝土结构构件截面应力重分布及其演变过程的相关研究涉及较少。
应力重分布问题是混凝土结构分析与设计所关注的重要问题之一[15],笔者以硫酸盐环境下轴向受压混凝土为研究对象,针对混凝土试件在硫酸盐侵蚀过程中的截面应力重分布问题,建立硫酸根离子在混凝土内的传输模型、混凝土损伤程度与硫酸根离子浓度和腐蚀时间之间的关系、考虑损伤程度影响的硫酸盐侵蚀混凝土腐蚀本构模型,在此基础上,建立硫酸盐侵蚀过程中轴心受压混凝土试件截面应力重分布过程的计算方法。
1 模型
1.1 扩散反应方程
(1)
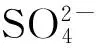
Dc=[φ+ω(c,t)]Dc0
(2)
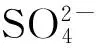
对于扩散反应方程(1),其初始和边界条件为
(3)
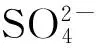
cs=φsc0
(4)
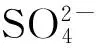
(5)
(6)
式中:kv为化学反应速率常数;cCa为混凝土孔溶液中钙离子浓度。
1.2 腐蚀损伤程度

(7)
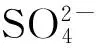
通过积分求解,式(7)变为
(8)

图1 混凝土腐蚀损伤程度与浓度及腐蚀时间的关系Fig.1 Relationship of concrete damage degree with sulfate concentration and corrosion time
1.3 腐蚀本构模型

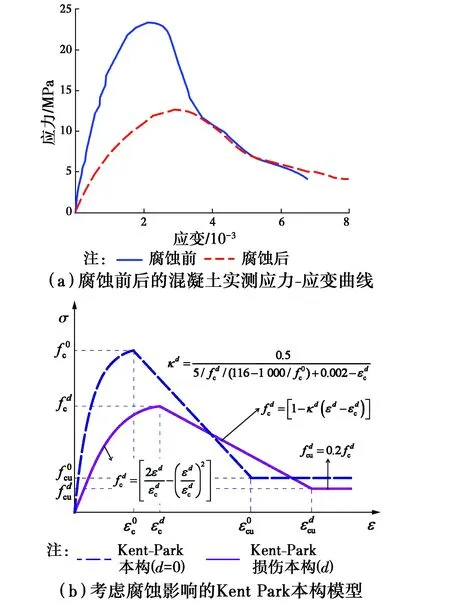
图2 混凝土腐蚀损伤本构模型Fig.2 Damage constitutive model of theconcrete due to sulfate attac
(9)

(10)
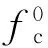
(11)

(12)

(13)

(14)
1.4 柱截面应力重分布
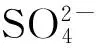
(15)
式中:N0为试件轴心受压荷载;dx和dy分别为试件截面尺寸微分;Aur为纵向钢筋截面面积;σs为纵向钢筋应力,按钢筋弹性强化本构模型确定[15]。
根据式(1)、式(6)、式(8)、式(9)和式(15),通过数值迭代法求解,可获得硫酸盐侵蚀过程中钢筋混凝土柱截面应力分布随损伤程度的变化规律。
2 数值求解
2.1 网格划分
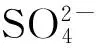
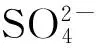
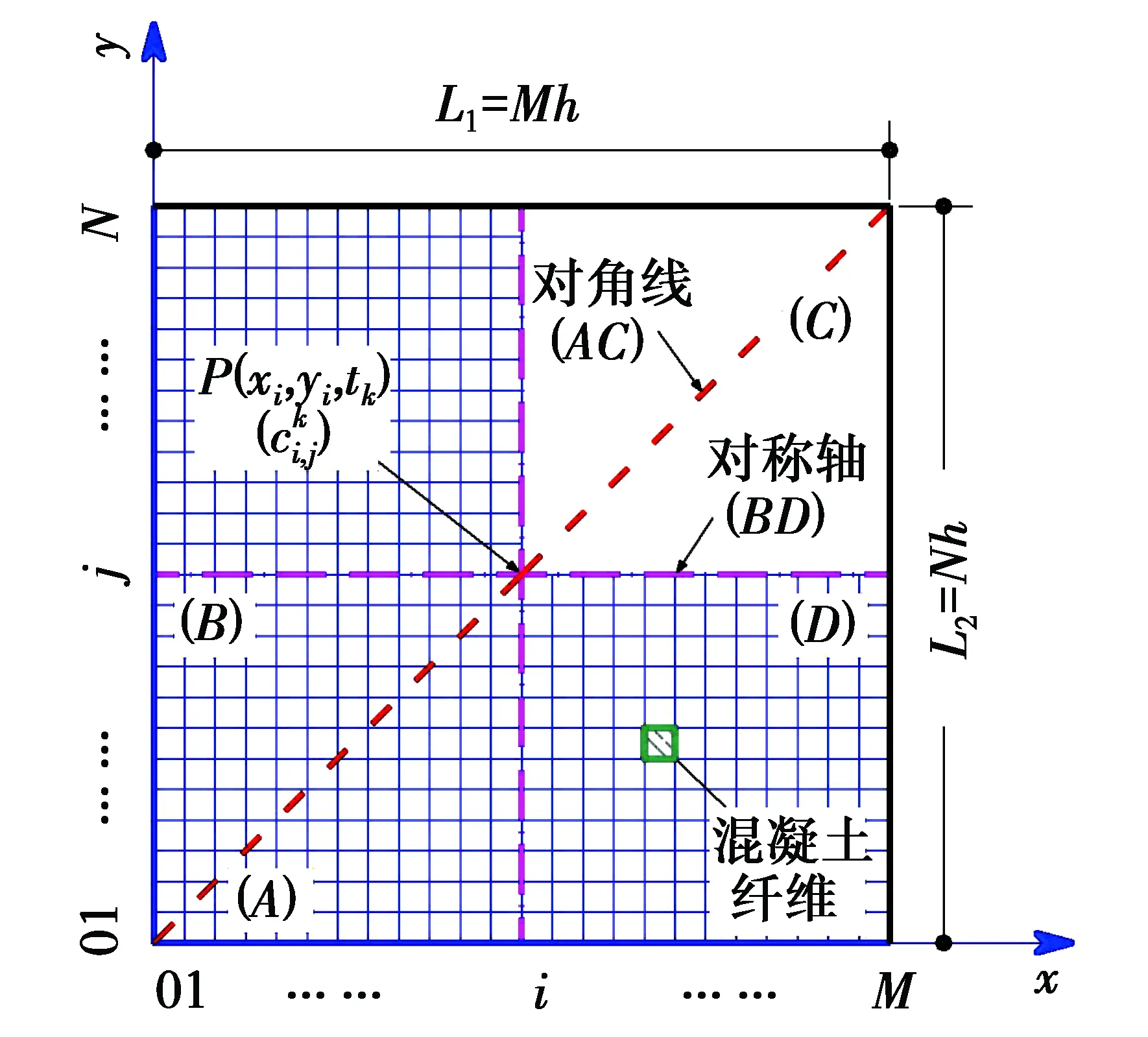
图3 混凝土试件截面网格划分Fig.3 Mesh of cross section of concrete specime
2.2 损伤程度计算
硫酸盐侵蚀过程中,混凝土损伤程度d(x,y,t)的计算式(8)是一个与硫酸根离子浓度相关的积分公式,需要按照图3所示的网格划分方法,进一步对式(8)进行数值离散。

图4 积分求解混凝土腐蚀损伤程度Fig.4 Integral calculation of concrete damage degre

(16)
式(16)表明,在腐蚀时间为tk时,混凝土试件截面位置(xi,yj)处的腐蚀损伤程度可通过图4中的阴影区面积S表征。
(17)
即,试件截面 (xi,yj) 处的混凝土腐蚀损伤程度为
(18)
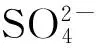
2.3 截面应力求解
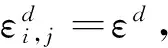
(19)
式中:e为试件截面纤维网格单元;M×N为网格单元的数目;Ace为网格单元面积。


图5 柱截面应力计算框图Fig.5 Calculating flowchart of column section’s stres
值分析轴压荷载和硫酸盐耦合作用下钢筋混凝土柱截面应力分布随腐蚀时间的变化规律。
3 数值算例
3.1 初始参数
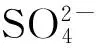
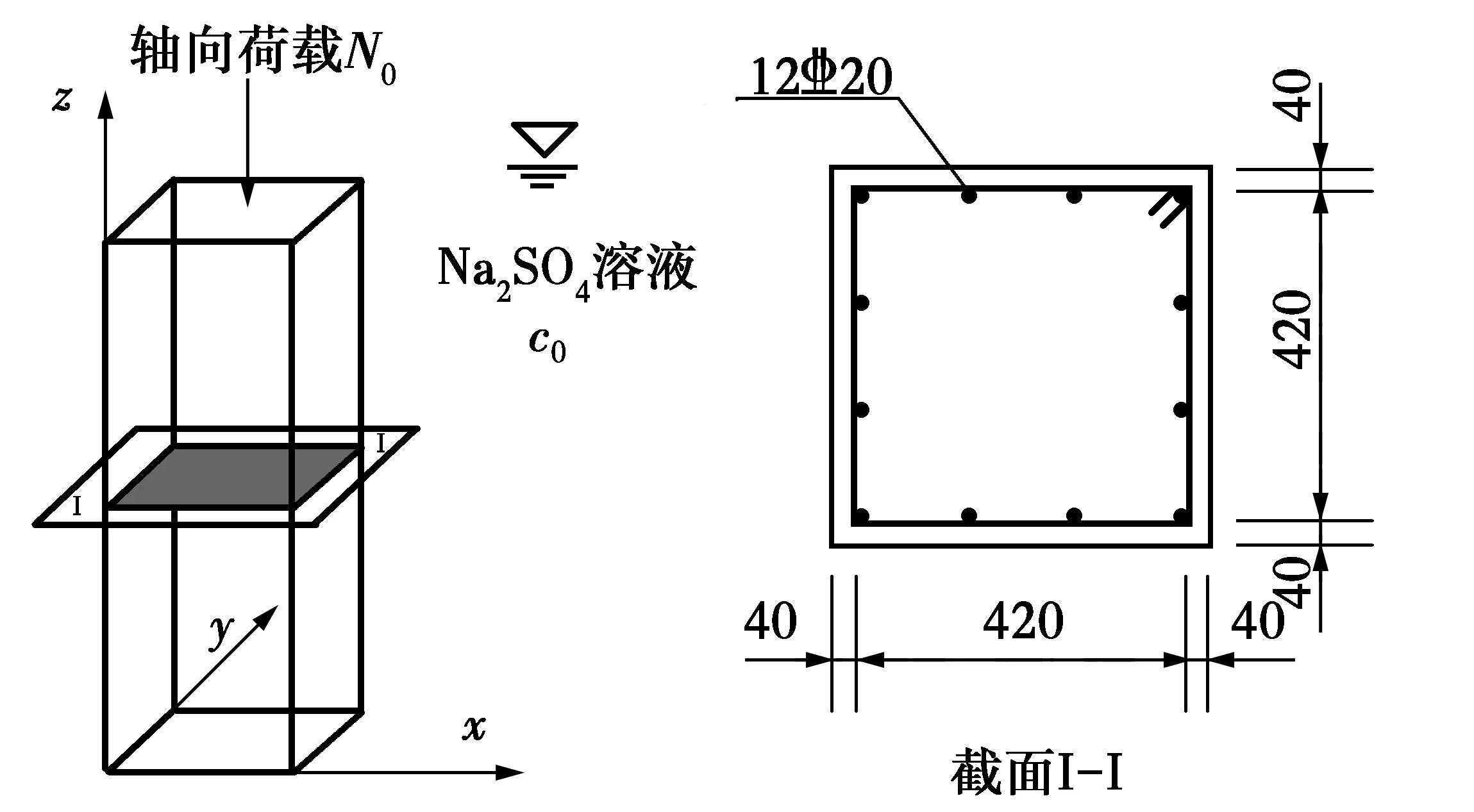
图6 混凝土柱截面配筋Fig.6 Reinforced concrete column sectio

强度等级抗压强度fc0/MPa峰值应变ε0c极限强度f0cu/MPa极限应变ε0cuC4026.80.00185.360.0056

表2 模型中的相关计算参数Table 2 Calculation parameters in the model
3.2 结果及分析

图7 柱截面上硫酸根离子浓度随截面位置与腐蚀时间的变化Fig.7 Time- and spatial-varying sulfate ion concentration in concrete column sectio
3.2.2 腐蚀损伤程度 硫酸盐侵蚀下柱截面的损伤状态含未损伤、损伤和剥落区,对应的混凝土损伤程度分别为d=0、0 图8 混凝土腐蚀损伤程度随截面位置与腐蚀时间的变化关系Fig.8 Time-and spatial-varying damage degree in concrete column sectio 3.2.3 应力应变曲线 图9给出了腐蚀4 000 d时钢筋混凝土柱截面不同位置处(d为各位置点的损伤程度)混凝土的应力应变曲线。从图中可以看出,腐蚀4 000 d时,各位置处混凝土的应力应变曲线形状基本一致,但峰值应力、峰值应变等参数随d的变化而变化,其中,混凝土的峰值应力随着d的增加而不断减小,而峰值应变随着d的增加而增大,如非对角线BC上点(10,25)(d=0.12)的峰值应力和峰值应变分别为23.58 MPa及1.93×10-3,而点(6,25)(d=0.53)的峰值应力和峰值应变分别为12.60 MPa及2.47×10-3,二者对比发现,前者混凝土的腐蚀损伤程度较小,其峰值应力是后者1.87倍,但峰值应变较后者小0.54×10-3。此外,从图9中还可知,混凝土软化段斜率随d的增加而减小,最后变为0,而极限应变增大。 图9 柱截面不同位置处的混凝土腐蚀损伤本构Fig.9 The concrete-corroded constitutive model at different positions of sectio 3.2.4 柱截面应变及名义弹性模量 在平截面假定的条件下,轴压混凝土柱截面应变仅与腐蚀时间有关,图10给出了硫酸盐侵蚀混凝土柱截面应变随腐蚀时间的变化规律。从图中可以看出,在竖向荷载3 000 kN作用下,从硫酸盐侵蚀前至腐蚀,混凝土柱截面应变从腐蚀前的0.42×10-3增加至腐蚀2 800 d时0.68×10-3,且其基本呈线性增加;而当腐蚀时间从2 800 d增加到7 500 d时,柱截面应变上升至1.90×10-3,超过混凝土的初始峰值应变(1.80×10-3),因此,在硫酸盐侵蚀混凝土的后期,其柱截面应变增加明显。此外,根据截面应变随腐蚀时间的变化,可计算硫酸盐侵蚀过程中混凝土名义弹性模量(E=N0A-1ε-1))随腐蚀时间的变化情况,图10表明,硫酸盐侵蚀过程中,混凝土的弹性模量随腐蚀时间的增加而降低。 图10 柱截面应变及混凝土名义弹性模量随腐蚀时间的变化Fig.10 Change of the section strain and the elastic modulus of concrete with the corrosion tim 图11 混凝土柱截面应力随截面位置与腐蚀时间的变化Fig.11 Time-and spatial-varying stress in 通过数值模拟,研究了轴心受压荷载和硫酸盐侵蚀耦合作用下钢筋混凝土柱截面内离子传输、腐蚀损伤演变、截面应变和应力的变化规律,结果表明: 1)硫酸盐侵蚀过程中,混凝土柱截面内硫酸根离子浓度呈梯度分布,且除了随腐蚀时间的增加而增加外,还明显受柱截面二维交互效应的影响。 2)在混凝土柱截面内存在硫酸盐腐蚀损伤区,该腐蚀损伤区随腐蚀时间逐渐向截面内部移动,且其宽度也逐渐增加。 3)在一定轴心受压荷载作用下,混凝土柱截面应变随腐蚀时间的增加而增加,且其名义弹性模量降低。 4)轴心受压荷载作用下,柱截面钢筋应力随硫酸盐腐蚀时间的增加而增加,而柱截面混凝土应力在未损伤区内随腐蚀时间的增加而增加,但在损伤区内随腐蚀时间的增加而呈现先增加后逐渐降低,可见,在硫酸盐侵蚀过程中,钢筋混凝土柱截面发生了明显的应力重分布现象。 [1] JIANG L, NIU D T. Study of deterioration of concrete exposed to different types of sulfate solutions under drying-wetting cycles [J]. Construction and Building Materials, 2016, 117: 88-98. [2] 姚明博, 李镜培. 混凝土灌注桩中混含硫酸盐的时变分布规律[J]. 土木建筑与环境工程, 2015, 37(5): 95-100. YAO M B, LI J P. Theoretical analysis of the time-varying distribution behavior of bored pile internal mixed sulfate [J]. Journal of Civil, Architectural & Environmental Engineering, 2015, 37(5): 95-100. (in Chinese) [3] 殷光吉, 左晓宝, 孙伟, 等. 硫酸盐侵蚀下水泥净浆膨胀应变计算[J]. 工程力学, 2015, 32(9): 119-125. YIN G J, ZUO X B, SUN W, et al. Numerical simulation of the expansive strain in cement paste subjected to sulfate attack [J]. Engineering Mechanics, 2015, 32(9): 119-125. (in Chinese) [4] SUN C, CHEN J, ZHU J, et al. A new diffusion model of sulfate ions in concrete[J]. Construction and Building Materials, 2013, 39: 39-45. [5] LORENTE S, YSSORCHE-CUBAYNES M P, AUGER J. Sulfate transfer through concrete: Migration and diffusion results [J]. Cement and Concrete Composites, 2011, 33(7): 735-741. [6] TAI I, CAVALARO S H P, SEGURA I, et al. Alternative methodology to consider damage and expansions in external sulfate attack modeling [J]. Cement and Concrete Research, 2014, 63: 105-116. [7] LIU Z, DE SCHUTTER G, DENG D, et al. Micro-analysis of the role of interfacial transition zone in “salt weathering” on concrete [J]. Construction and Building Materials, 2010, 24(11): 2052-2059. [8] JIANG L, NIU D T, SUN Y Z, et al. Ultrasonic testing and microscopic analysis on concrete under sulfate attack and cyclic environment [J]. Journal of Central South University, 2014, 21(12): 4723-4731. [9] YANG D Y, LUO J J. The damage of concrete under flexural loading and salt solution [J]. Construction and Building Materials, 2012, 36(4): 129-134. [10] SONG H, CHEN J K. Effect of damage evolution on poisson's ratio of concrete under sulfate attack [J]. Acta Mechanica Solida Sinica, 2011, 24(3): 209-215. [11] MIRVALAD S, NOKKEN M. Studying thaumasite sulfate attack using compressive strength and ultrasonic pulse velocity [J]. Materials and Structures, 2016, 49(10): 4131-4146. [12] 梁咏宁, 袁迎曙. 硫酸盐腐蚀后混凝土单轴受压本构关系[J]. 哈尔滨工业大学学报, 2008, 40(4): 532-535. LIANG Y N, YUAN Y S. Constitutive relation of sulfate attacked concrete under uniaxial compression [J]. Journal of Harbin Institute of Technology, 2008, 40(4), 532-535. (in Chinese) [13] 刘汉昆, 李杰. 受侵蚀混凝土本构关系[J]. 建筑材料学报, 2011, 14(6): 736-741. LIU H K, LI J. Constitutive law of attacked concrete [J]. Journal of Building Materials, 2011, 14(6): 736-741. (in Chinese) [14] 邹笃建, 刘铁军, 滕军. 硫酸钠侵蚀混凝土柱动态抗压特性试验研究[J]. 建筑材料学报, 2011, 14(6): 742-745. ZOU D J, LIU T J, TENG J. Research on dynamics compressive behavior of plain concrete columns suffering from sulfate attack [J]. Journal of Building Materials, 2011, 14(6): 742-745. (in Chinese) [15] 过镇海. 钢筋混凝土原理[M]. 北京: 清华大学出版社, 2013. GUO Z H. Reinforced concrete principle [J]. Beijing: Tsinghua University Press, 2013. (in Chinese) [16] ZUO X B, SUN W, YU C. Numerical investigation on expansive volume strain in concrete subjected to sulfate attack [J]. Construction and Building Materials, 2012, 36(4): 404-410. [17] 左晓宝, 孙伟. 硫酸盐侵蚀下的混凝土损伤破坏全过程[J]. 硅酸盐学报, 2009, 37(7): 1063-1067. ZUO X B, SUN W. Full process analysis of damage and failure of concrete subjected to external sulfate attack [J]. Journal of the Chinese Ceramic Society, 2009, 37(7): 1063-1067. (in Chinese) [18] BONTEMPI F, BIONDINI F, DAN M F, et al. Cellular automata approach to durability analysis of concrete structures in aggressive environments [J]. Journal of Structural Engineering,2004,130(11): 1724-1737. [19] SCOTT B D, PARK R, PRIESTLEY M J N. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates [J]. ACI Journal, 1982, 79(2): 13-27. [20] 陆金甫. 偏微分方程数值解法[M]. 北京: 清华大学出版社, 2004. LU J F. Numerical methods for partial differential equations [M]. Beijing: Tsinghua University Press, 2004. (in Chinese) [21] ZUO X B, SUN W, LI H, et al. Modeling of diffusion-reaction behavior of sulfate ion in concrete under sulfate environments [J]. Computers and Concrete, An International Journal, 2012, 10(1): 47-51. 2017-05-25 National Natural Science Foundation of China(No. 51378262, 51778297); Natural Science Foundation of Jiangsu Province (No. BK20141396) Numericalanalysisontime-varyingprocessofstressinreinforcedconcretecolumnsubjectedtoaxialcompressionandsulfateattack WangJialin,ZuoXiaobao,MaQiang,YinGuangji,TangYujuan (Department of Civil Engineering, Nanjing University of Science & Technology, Nanjing 210094, P. R. China) In order to investigate the stress responses of reinforced concrete column subjected to the couplings of axial compression and sulfate attack, this paper applied an existed diffusion-reaction equation of sulfation in concrete to obtain a relationship between the sulfate-induced damage degree and the ion concentration and the corrosion time. On the basis, a concrete-corroded constitutive model related to the damage degree and a calculating approach for stress responses of concrete under the couplings of axial compression and sulfate attack were proposed. Through numerical solution on these models, the changes of sulfate ion concentration, damage degree, strain and stress in concrete with the corrosion time were analyzed. Results show that the sulfate ion concentration and damage degree has a gradient distribution in concrete, and they are obviously influenced by the two-dimensional interactions in the cross section. With the increase of corrosion time, the damage zone gradually moves inward the cross section, and its width has a gradual increase, and the stress in the damage zone increases firstly and then has a gradual decrease, but in the no damage zone, the stress has a basically linear increase. In the process of sulfate attack, there produces the stress redistribution in concrete under axial compression. concrete; sulfate attack; axial compression; damage; stress redistribution 10.11835/j.issn.1674-4764.2018.01.005 TU375.3 A 1674-4764(2018)01-0030-09 2017-05-25 国家自然科学基金 (51378262、51778297);江苏省自然科学基金 (BK20141396) 王佳林(1994-),男,主要从事混凝土材料与结构研究,E-mail:jialinwang1994@163.com。 左晓宝(通信作者),男,教授,博士生导师,E-mail:xbzuo@sina.com。 AuthorbriefWang Jialin (1994- ), main research interests: concrete materials and concrete structures,E-mail:jialinwang1994@163.com. Zuo Xiaobao(corresponding author), professor, doctoral supervisor,E-mail:xbzuo@sina.com. (编辑 胡英奎)
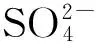



4 结论
