复习课，用深度教学促进深度学习

吴守元

近年来，有一种观点：只有降低教学难度才能推行素质教育。结果，首先是浅显机械的课堂教学，然后是简单大量的重复练习，最后是没有任何批改和评讲价值的考查测试，教师不需要做任何深度的准备就可以直接走进课堂。

笔者认为这样的教学是不能提高学生素质的，反而会降低学生的素质，比如畏难、回避、放弃等。因此，我们应该认真研究和实践深度教学。当教学完一章或者一个单元后，必然会有复习课，很多复习课都是按节次顺序总结归纳，求全求细，找出大量与知识点一一对应的习题反复练习，以強化记忆和应付考试。那么，复习课的深度教学应该以怎样的内容和形式呈现呢？现以人教版八年级物理第十章《浮力》为例，谈一谈以复习课为契机，用深度教学促进学生深度学习。

一、打破节次顺序，重组和整合

分节次上完《浮力》三小节后，首先可以进行如下形式的全章复习。

（一）看事物的联系

1.利用物理量之间的联系进行有价值的猜想

因为m=ρv，m排可以把ρ液和V排联系起来，m排越大，F浮越大。同种物理量大小的比较更合理更有意义。而G=mg，G排=m排g，G排越大，F浮越大。所以决定把F浮与G排联系起来研究，探究F浮与G排的大小关系。

2.完全浸没条件下，利用V=V排把物体和液体联系起来

让物体完全浸没在液体中时，V=V排 ，而G=ρ物Vg，F浮=ρ液V排g，两式相比有G/F浮=ρ物/ρ液。利用弹簧测力计可以测出G和F浮，那么，已知ρ液可以测ρ物。反过来，已知ρ物可以测ρ液。

3.利用漂浮条件把物体和液体联系起来

漂浮条件下：F浮=G物，ρ液V排g=ρ物Vg，ρ物/ρ液=V排/V物。利用刻度尺，测出漂浮在水面的长方体的整体高度和露出水面的部分高度，即可测出这个物体的密度，反之，已知物体的密度又可以用这个规律测出待测液体的密度。

4.利用Δh=V排/S把液体压强和浮力联系起来

一个物体放入盛有液体的柱状容器中，物体会排开液体受到浮力，液面升高，容器底受到的压强增大。Δh=V排/S ，Δp=ρ液gΔh=ρ液gV排/S=F浮/S，其实，物体放入液体中后，液体要对物体施加一个浮力，由于力的作用是相互的，物体要对液体施加一个等大的反作用力，传到容器底，所以Δp=ΔF/S=F浮/S。

看事物的联系，有利于找出事物的规律。

（二）看事物的本质

1.浮力大小的本质

由阿基米德原理F浮=G排可知，浮力大小等于物体排开液体的重力，只与液体的密度和物体排开的液体体积有关，与物体的密度、体积、液体的体积等都无关。

2.物体沉浮的本质

[浮沉＼&力比较＼&密度比较＼&上浮＼&F浮> G＼&ρ液>ρ物＼&悬浮＼&F浮= G＼&ρ液=ρ物＼&下沉＼&F浮< G＼&ρ液<ρ物＼&]

物体的浮沉，不是决定于浮力的大小，也不是决定于重力的大小，而是浮力与重力对抗的结果；实质是物体密度和液体密度的大小比较的结果。

看事物的本质，不至于被表面现象迷惑。

（三）看事物的区别

1.漂浮和悬浮的区别

[漂浮＼&悬浮＼&部分进入V排=nV物（n<1）＼&完全浸没V排=V物＼&ρ物<ρ液 ρ物=nρ液（n<1）＼&ρ物=ρ液 ρ物=ρ液＼&]

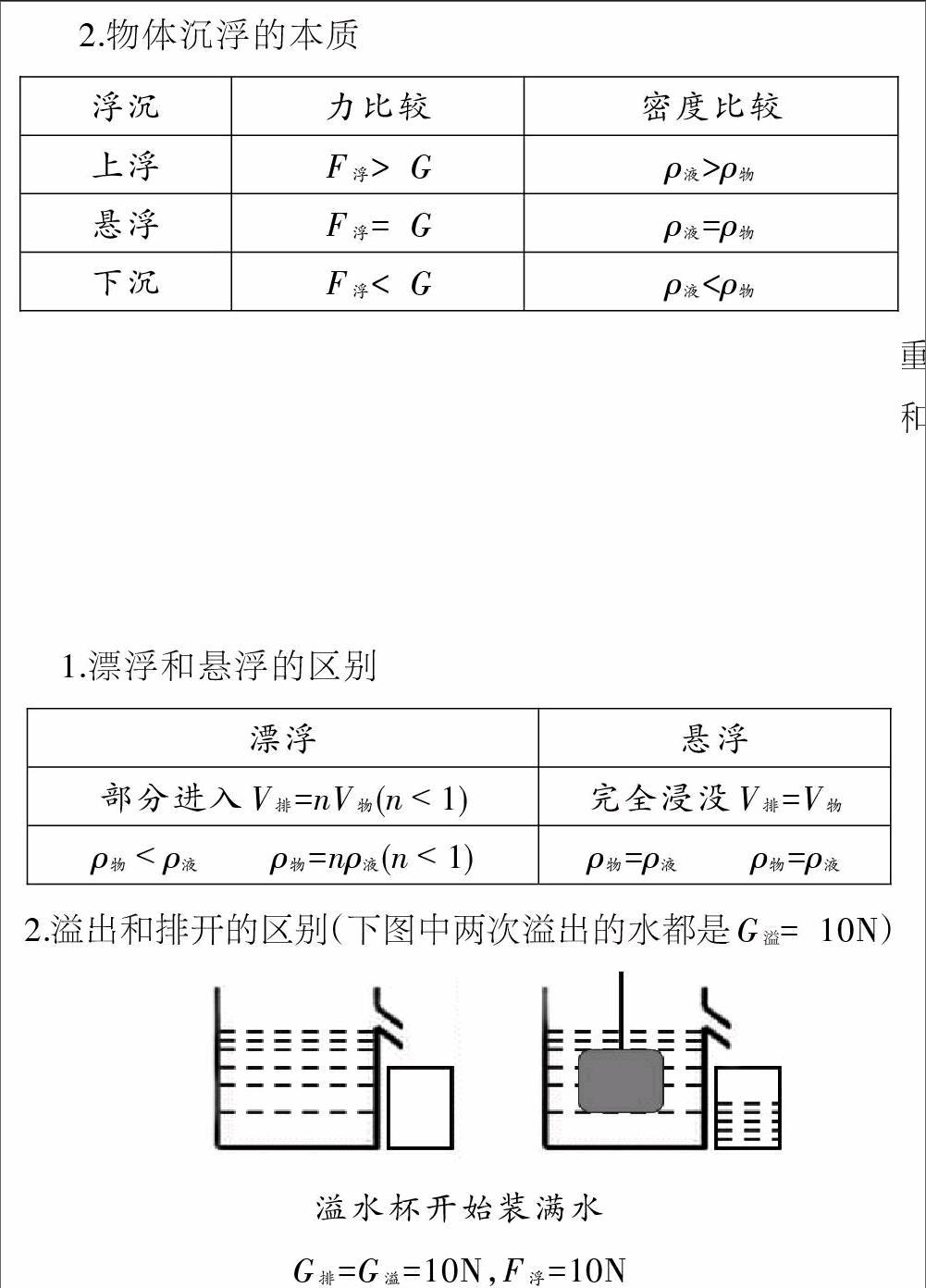
2.溢出和排开的区别（下图中两次溢出的水都是G溢= 10N）

溢水杯开始装满水

G排=G溢=10N，F浮=10N

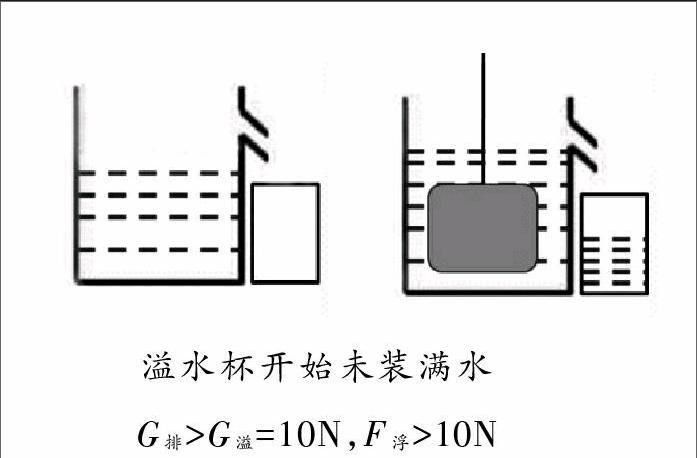
溢水杯开始未装满水

G排>G溢=10N，F浮>10N

例：将质量为120g的物体放入盛水的溢水杯中，当物体静止时，溢水杯中溢出了100cm3的水，则物体可能（g取10N/kg）（ABCD）

A.漂浮在水面上 B.悬浮在水中

C.沉在溢水杯底部 D.受到1.2N的浮力

看事物间的区别，更容易看清事物本身。

这样的全章复习，又称“整体深度复习”，不仅能够抓住本章的重难点、易错点，而且学生复习起来有一定的挑战性，不会感觉到重复、枯燥，更重要的是培养学生从联系、本质、区别等角度观察分析事物，并把这种习惯和能力由课内扩展到课外。

二、归类比较，构建知识体系

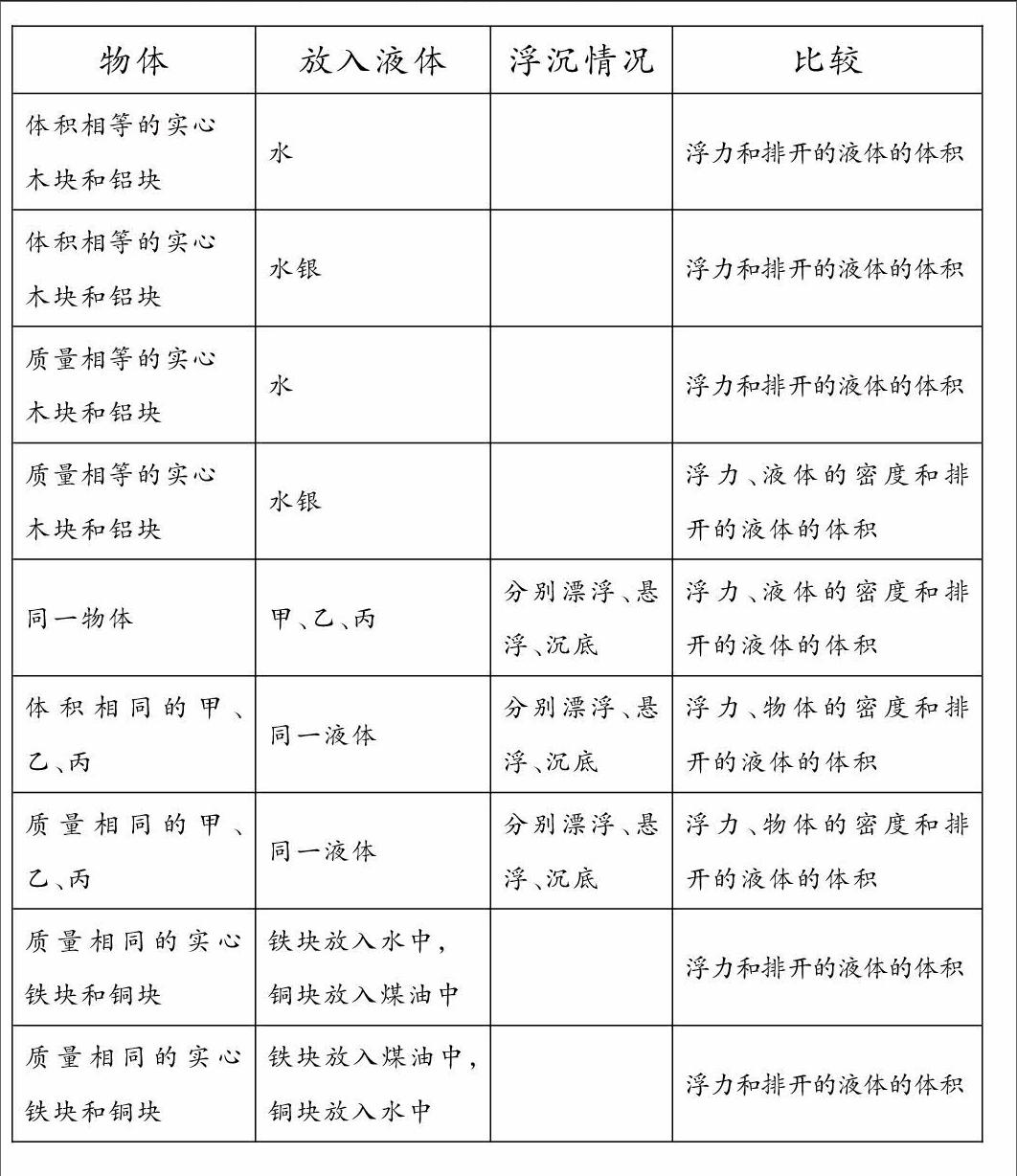
浮沉题是重点，也是难点，学生要做很多相关的练习，但是如果有了前面的重组和整合，教师将积累转化成如下表的九大问题，集中起来让学生讨论和解决，将大大提高课堂效率，培养学生清理同类问题、找出同与不同、构建知识体系的习惯和能力，称之为 “局部深度复习”。

[物体＼&放入液体＼&浮沉情况＼&比较＼&体积相等的实心

木块和铝块＼&水＼&＼&浮力和排开的液体的体积＼&体积相等的实心

木块和铝块＼&水银＼&＼&浮力和排开的液体的体积＼&质量相等的实心

木块和铝块＼&水＼&＼&浮力和排开的液体的体积＼&质量相等的实心

木块和铝块＼&水银＼&＼&浮力、液体的密度和排开的液体的体积＼&同一物体＼&甲、乙、丙＼&分别漂浮、悬浮、沉底＼&浮力、液体的密度和排开的液体的体积＼&体积相同的甲、乙、丙＼&同一液体＼&分别漂浮、悬浮、沉底＼&浮力、物体的密度和排开的液体的体积＼&质量相同的甲、乙、丙＼&同一液体＼&分别漂浮、悬浮、沉底＼&浮力、物体的密度和排开的液体的体积＼&质量相同的实心铁块和铜块＼&铁块放入水中，

铜块放入煤油中＼&＼&浮力和排开的液体的体积＼&质量相同的实心铁块和铜块＼&铁块放入煤油中，铜块放入水中＼&＼&浮力和排开的液体的体积＼&]

三、立足某个问题，纵深延展

通过对一个普通的例题：“一个边长为10cm的正方体均匀木块，漂浮在水面上，水下部分深6cm。已知ρ水为1.0×103 kg/m3，g取10N/kg，求木块的密度。”进行如下的变形和展开。

（一）液体不变，物体变

1.物体表面变，将木块露出部分切割，结果会怎样？漂浮在水中的蠟烛慢慢燃烧会是怎样的情形？

2.物体本质变，另一个边长为10cm的正方体均匀物体漂浮在水面，露出3cm高，求这个物体的密度，建立只用刻度尺测漂浮在水面的正方体的密度的方案。

（二）物体不变，液体变

1.将木块放入酒精中、盐水（给密度）中，求液面下的深度，比较三个深度得出什么结论？

2.密度计上面的刻度是上大下小还是上小下大？

3.轮船从河里开到海里，什么不变什么变？

（三）物体变，液体也变

1.体积相同的木块和铜块，分别漂浮在水中和水银中（给出四种物质的密度），比较它们受到的浮力和排开的液体的体积。

2.质量相同的木块和铜块，分别漂浮在水中和水银中（给出四种物质的密度），比较它们受到的浮力和排开的液体的体积。

无论条件和问题怎么变化，所有的漂浮问题几乎都可以归结为漂浮条件下的V排/V物=ρ物/ρ液，通过这种由浅入深、以点带面、向纵深延展的训练，培养学生寻找规律和运用规律的习惯和能力，称之为“延展深度复习”。

四、列举典型例题，培养分析和解决问题的能力

通过典型的例题，帮助和引导学生找出和建立事物变化过程中潜藏的关系，并及时挖掘这个例题隐含的其他问题和物理方案，从而举一反三，培养学生通过寻找和建立物理关系来分析和解决问题的习惯和能力，称之为“典例深度复习”。

例1：用弹簧测力计竖直挂一铁球，当铁球的三分之二露出水面时，弹簧测力计示数为4N；当铁球浸入水中一半体积时，弹簧测力计示数为1N，取下该铁球放入水中，铁球静止时受到的浮力是（ D ）

A.18N B.14N C.8N D.10N

方法一：题述两种情况下的条件都有关竖直方向上的三力平衡，可以设定两个未知量，完全浸没时的浮力F浮（可以用来表示露出不同体积时的浮力）和重力G，列两个方程，求出F浮=18N，G=10N。首先要判断铁球静止时的状态，才能得出浮力为10N。

方法二：当物体从[13]V浸入到[12]V时，弹簧测力计的示数减小了3N，说明浮力增大了3N，即[12]V-[13]V=[16]V浸入时的浮力是3N，完全浸没的浮力是18N。

拓展：铁球的密度是多少？铁球漂浮时露出几分之几？把露出部分刚好按入水中静止需要多大的力？

根据该拓展建立一个方案，只有弹簧测力计这一种测量工具，测不能漂浮在水中的物体的密度；根据以下例2建立一个方案，只有刻度尺这一种测量工具，已知物体的密度，测某液体的密度。

例2：取边长为a的正方体木块放入装有适量密度为ρ0的液体的烧杯中，待其静止后用刻度尺测出有[25]高度露出液面（如图甲）。将B物体放在木块中央静止后用刻度尺测出此时木块露出液面的高度为h1（如图乙）。用体积可忽略不计的细线将物体B系在木块中央，放入液体中静止后测出此时木块露出液面高度h2（如图丙）。求B物体的密度ρB（用相关的物理量表示）。

分析：从甲到乙，增加的浮力即为增加的重力，也就是木块的重力GB=ρ0S（[25]a-h1）g；从乙到丙总重力没有变，总浮力没有变，排开液体的总体积没有变。木块浸入液体体积的减少量就是B的体积VB=S（h2-h1），ρB=GB/VBg=ρ0S（[25]a-h1）g/S（h2-h1）g=ρ0（[25]a-h1）/（h2-h1）。

教学中要纠正“广播体操式的简单重复”，实施“瑜伽式的深度延展”。事实上，其他课型，如新授课、习题课、专题课、评讲课都可以而且应该进行深度教学，深度教学最忌讳贪多求全，深度教学需要深厚的积累和反复的准备。让我们在每一节课、每一次作业、每一次考试中都用心设置一些深度元素吧，这是一个有待系统研究和实践的课题。

（作者单位：应城市教研室）