Mackey-Glass系统欧拉法的动力性

庄小兰，王 琦

（广东工业大学 应用数学学院，广东广州510540）

Mackey-Glass系统欧拉法的动力性

庄小兰，王 琦

（广东工业大学 应用数学学院，广东广州510540）

应用欧拉法研究了Mackey-Glass系统的动力性。证明了随着延迟的增加，正的不动点处将出现一系列霍普夫分支，进而分析了不动点的稳定性，最后，通过数值实验验证了理论结果的正确性。

Mackey-Glass系统；欧拉法；霍普夫分支；稳定性

目前，延迟微分方程分支理论的研究与应用已超过了原来数学学科的界限，成为了动力系统理论［1］研究的一个热点问题，延迟项的数值估计也成为了延迟微分方程数值研究中的一个重要方面［2］。文献［3-11］研究了延迟微分方程的局部霍普夫分支，但对其相关的研究仍是一个富有挑战性的课题。王晓燕等［12］研究了二级Runge-Kutta法用于Van der Pol方程后的离散化系统的霍普夫分支，通过对其特征根的讨论给出离散化系统的稳定区域，进一步得到数值霍普夫分支值，最后通过数值算例验证数值霍普夫分支对精确解的逼近行为。2006年，丁效华等［13］通过前向欧拉方法和离散系统的动力学研究得到一个Nicholson’s blowfies方程，在这之前，Wei和Li［14］已经得出产生霍普夫分支的条件和分支周期解的稳定性的结论，他们应用规范型理论和中心流形定理不仅讨论了Nicholson’s blowfies方程的线性稳定性，也给出了分支周期解的稳定性。张春蕊［15］利用Runge-Kutta方法研究了一阶延迟微分方程的数值霍普夫分支，并证明了数值霍普夫分支的存在性。

对于延迟微分方程

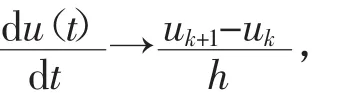
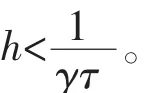
1 正平衡点的稳定性和局部霍普夫分支

令 p（t）=θx（t），则方程（1）变成

令 u（t）=x（τt），则方程（2）就可以写成

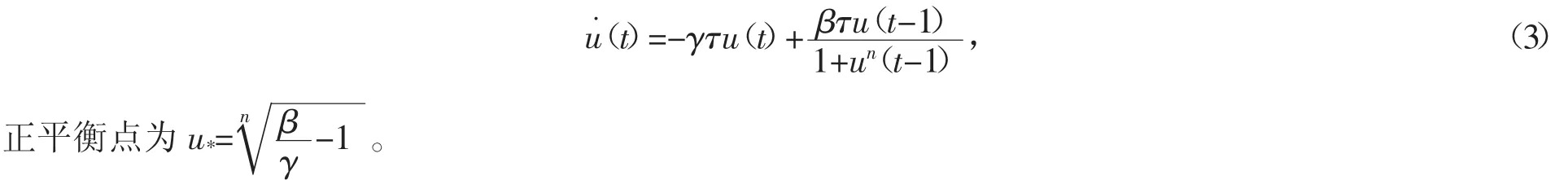
将欧拉法用于方程（3），有

设 yk=uk-u*，那么，有

通过引入一个新的变量 Yk=（yk，yk-1，…，yk-m）T，有映射

其中，F=（F0，F1，…，Fm）T，

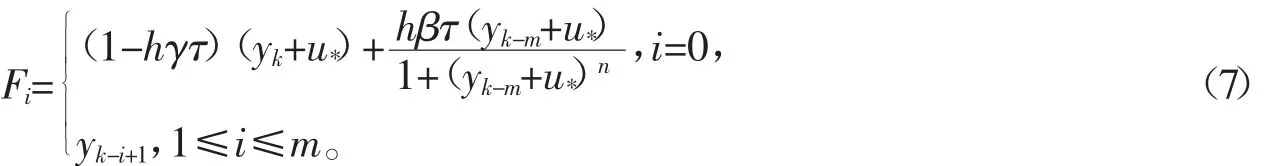
显然，原点是映射（6）的一个不动点，并且映射（6）的线性部分是

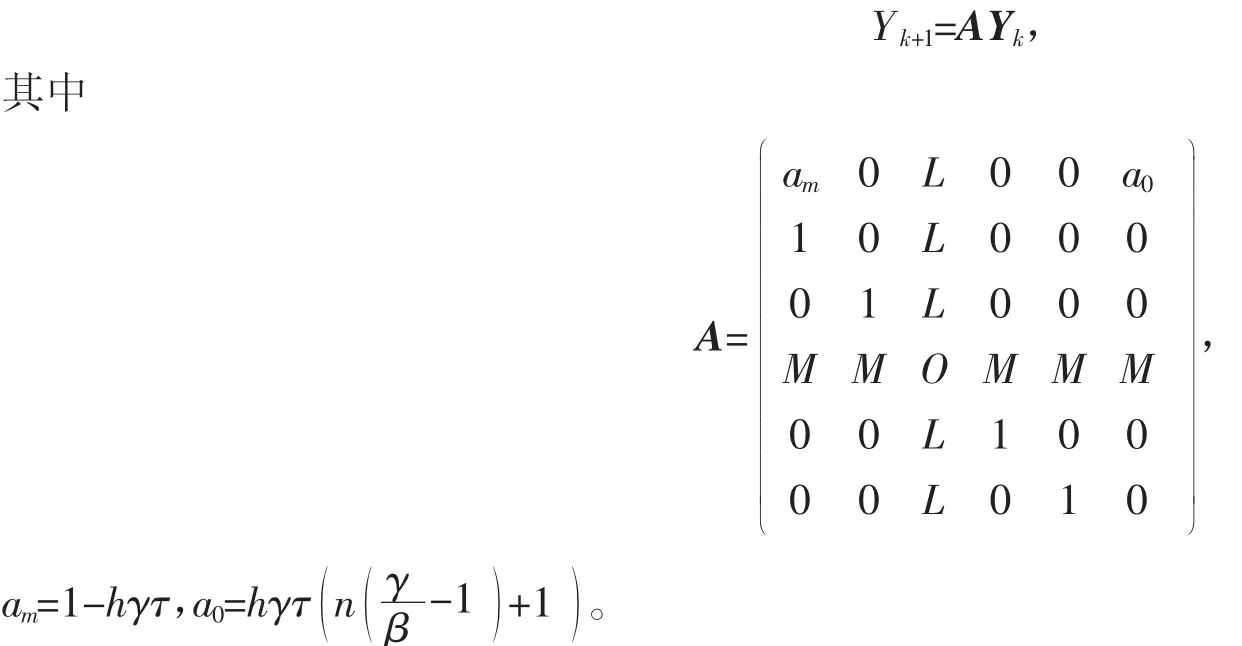
因此，A的特征方程为

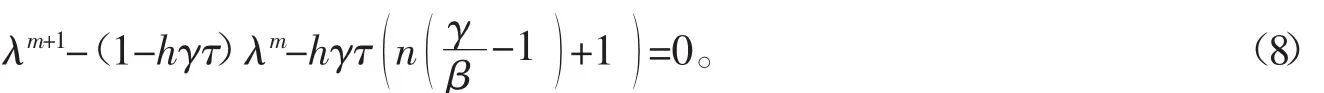
引理1 对于充分小的正数τ＞0，方程（8）的所有根的模都小于1。

第二，假新闻泛滥。随着人工智能不断成熟，在制造假新闻这一领域里，AI极有可能成为利益方最好的工具，而媒体正是利益方输送信息最好的渠道。利用人工智能技术进行音视频造假、机器人水军生产大量虚假新闻和评论等等，已形成一个“灰色产业链”，其推动力便是对利益和权力的追求。这一现象在 2016 年美国大选中就有所显现，各种假新闻对总统选举产生了巨大影响，时至今日“通俄门”事件仍在美国发酵。由此发展，AI在未来新闻业的融合极有可能造成假新闻泛滥的局面，这说明未来新闻业的发展或许很大一部分是数据权利的博弈。在这场博弈中，人们看到的世界是真实的世界吗？无疑，新闻的真实性会受到严重的冲击与挑战。

证明 当τ=0时，方程（8）等价于λm+1-λm=0，方程有一个m重根和一个单根λ=1。

考虑到方程（8）的根 λ（τ），使得 λ（0）=1。

这个根连续取决于τ，方程（8）是关于τ可微的，有

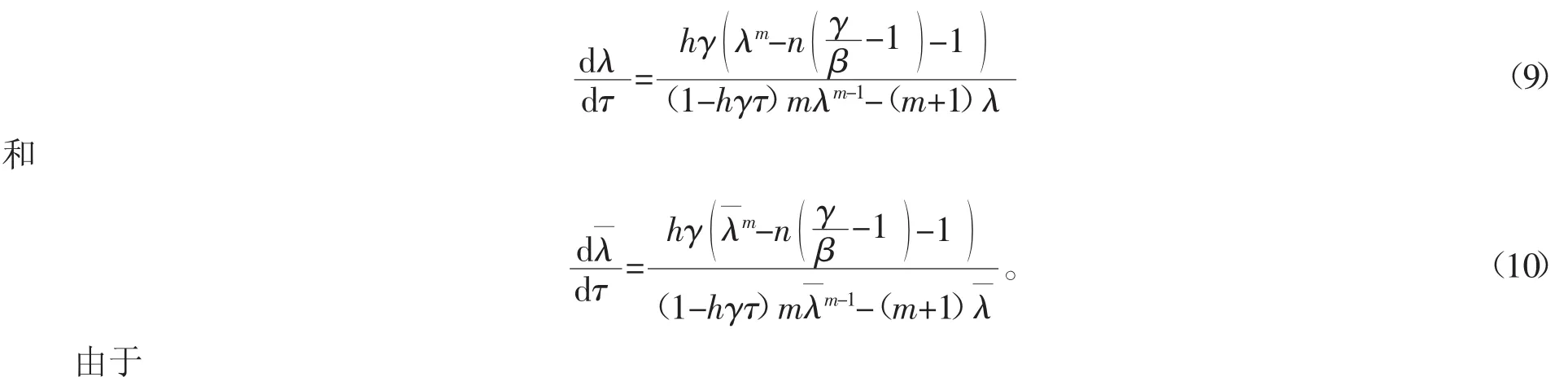
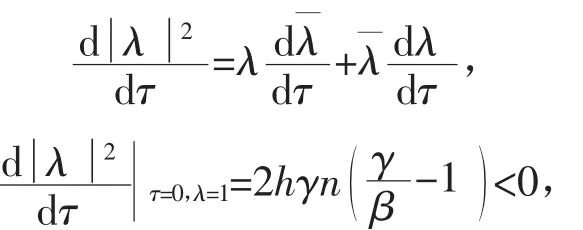
所以，随着τ＞0，λ不能穿过1。因此，对于充分小的正数τ＞0，方程（8）的所有特征根都在单位圆内。

用 eiω表示单位圆上的根，则当 ω∈（0，π］时，eiω是方程（8）的根，当且仅当

由方程（13），得

是正的，sin ω（ω∈［0，π］）和 sin mω 同号，因此，如果，根据引理2，存在一个序列

证明 根据方程（9）和（10），有

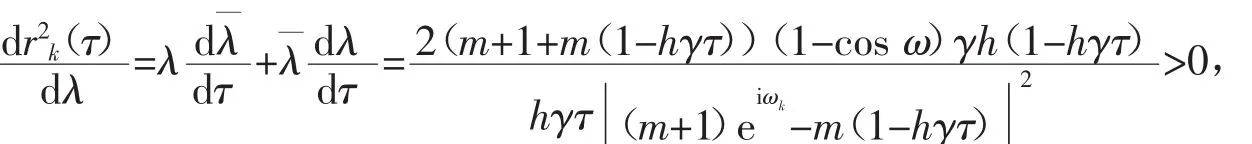
因此，结论得证。

证明 由引理1和2，应用文献［16］推论2.4，得出以下结论：

由引理 1 和 2，知道如果 τ∈（0，τ0］，那么方程（8）的所有根的模都小于 1；如果 τ=τ0，那么方程（8）除了外的根的模都小于1，此外，由儒歇定理，关于模大于1的特征值的个数自然得到。

引理4的特殊性质立即得到方程（5）的零解稳定性，即方程（4）的正不动点u=u*。所以我们有关于方程（4）的以下定理。

2 数值实验

本节的目的是通过一些实例来检验第1节的结果，其中β=0.2，β=0.1，n=10。

根据定理 1 和表 1，结合图 1～4，可以得到：当 τ∈［0，τ0）时，方程（4）的所有数值解都是渐近稳定的；当 τ＞τ0时，数值解不稳定。

表1 不同步长下分支点的值

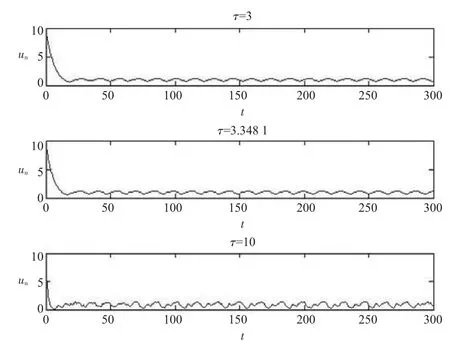
图1 方程（4）的数值解，步长h=1/2

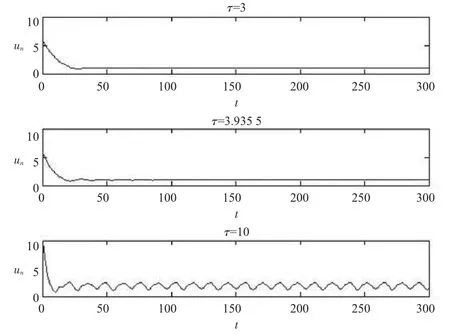
图2 方程（4）的数值解，步长h=1/4

图3 方程（4）的数值解，步长h=1/8

图4 方程（4）的数值解，步长h=1/16

［1］KUANGY.Delay differentialequationswith applications in population dynamics［M］.Boston,MA:Academic Press,1993.

［2］LID,LIUM Z.Runge-Kuttamethods for themulti-pantograph delay equation［J］.Applied Mathematics&Computation,2005,163（1）:383-395.

［3］LIAO X,LIS,CHEN G.Bifurcation analysis on a two-neuron system with distributed delays in the frequency domain［J］.NeuralNetworks,2004,17（4）:545.

［4］LIX,RUANS,WEIJ.Stability and Bifurcation in Delay-Differential Equationswith Two Delays［J］.Journal of Mathematical Analysis&Applications,1999,236（2）:254-280.

［5］GUOS,HUANG L.Hopf bifurcating periodic orbits in a ring of neurons with delays［J］.Physica DNonlinear Phenomena,2003,183（1-2）:19-44.

［6］YUANS,HANM.Bifurcation analysisofa chemistmodel with two distributed delays［J］.Chaos,Solitonsand Frctals,2004,20:995-1004.

［7］魏俊杰.向日葵方程的 Hopf分支［J］.应用数学学报,1996,19（1）:73-79.

［8］魏俊杰,黄启昌.以滞量为参数的向日葵方程的Hopf分支［J］.科学通报,1995（3）:198-200.

［9］WEIJ,LIM Y.Hopfbifurcation analysis in a delayed Nicholson blowfliesequation［J］.Nonlinear Analysis TheoryMethods&Applications,2005,60（7）:1351-1367.

［10］MEESA,CHUA LO.The Hopfbifurcation theorem and its applications to nonlinear oscillations in circuits and systems［J］.Circuits&Systems IEEETransactionson,1979,26（4）:235-254.

［11］MOIOLA JL,CHENGR.Frequency domain approach to computation and analysisofbifurcationsand limitcycles:a tutorial［J］.International JournalofBifurcation&Chaos,1993,3:843-867.

［12］王晓燕,李立.二级Runge-Kutta法用于Van der Pol方程的数值Hopf分支问题［J］.黑龙江科技信息,2008（22）:132.

［13］DING X,LIW.Stability and bifurcation of numerical discretization Nicholson blowflies equation with delay ［J］.Discrete Dynamics in Nature&Society,2006（1）:520-530.

［14］WEIJ,LIM Y.Hopf bifurcation analysis in a delayed Nicholson blow fliese quation［J］.Nonlinear Analysis Theory Methods&Applications,2005,60（7）:1351-1367.

［15］张春蕊.延迟微分方程稳定性与Hopf分支分析［D］.哈尔滨:哈尔滨工业大学,2003.

［16］RUAN S,WEIJ.On the zeros of transcendental functions with applications to stability of delay differential equations with two delays［J］.DynamicsofContinuous Discrete&Impulsive Systems,2003,10（6）:863-874.

Dynam icsof Eulermethod for Mackey-Glasssystem

ZHUANG Xiao-lan,WANG Qi
（School of Applied Mathematics,Guangdong University of Technology,Guangzhou 510540,China）

In this article,we study the dynamics of Mackey-Glass system applied in Eulermethod.We show a sequence of Hopf bifurcations occur at the positive fixed point as the delay increasing.And we analyze the stability of the fixed point.At last,by giving somenumerical experiments verify the correctnessof Eulermethod.

Mackey-Glasssystem;Eulermethod;Hopf bifurcations;stability

O29

A

1008-0171（2017）06-0006-06

2017-04-20

庄小兰（1993-），女，广东遂溪人，广东工业大学硕士研究生。

王桂珍 foshanwgzh@163.com】