城市供水管网优化调度研究现状

林英姿 ，宋成果

（1.吉林建筑大学 松辽流域水环境教育部重点实验室，长春 130118；2.吉林省城市水资源与水环境修复工程实验室，长春 130118；3.吉林建筑大学 市政与环境工程学院，长春 130118）

设计与施工

城市供水管网优化调度研究现状

林英姿1，2，宋成果3

（1.吉林建筑大学 松辽流域水环境教育部重点实验室，长春 130118；2.吉林省城市水资源与水环境修复工程实验室，长春 130118；3.吉林建筑大学 市政与环境工程学院，长春 130118）

简要介绍了优化调度的主要内容及研究现状，供水管网的优化建模及算法求解。优化调度能够确保管网处于最优运行状态，使管网运行及维护成本得到降低，最终社会及经济效益得到改善。

供水管网；用水量预测；管网模型；优化调度

1 优化调度内涵

城市供水系统的优化调度即在保证满足用户用水需求的前提下，利用管网在线监测系统所体现的管网运行状况和数据或根据科学合理的预测方法，建立供水管网微观模型，并结合优化调度模型，运用数学最优化技术，从所有计算得出的调度方案中确定一个安全性最高、经济型最好的运行方案，从而确定各个时段的用水量及泵站运行状态，使效益最大化。

2 国内外研究现状

2.1 城市用水量预测

在进行优化调度前，需先对调度周期内的用水量进行科学合理的预测。优化调度用的水量预测属于短期用水量预测，即根据以往用水量数据及用水量影响因素对调度周期的用水量做出科学合理预测。

目前预测用水量的方法有很多，常用的预测方法可归纳为两类：一类是回归分析方法，由于回归分析方法所需资料的种类及数量较多，且无法准确测得全部数据，因此，用水量预测不宜使用回归分析法。另一类是时间序列分析方法，这是一种分析各种相关数据集合的方法，时间序列分析方法的3种主要方法，包括指数平滑法和自回归－移动平均模型主要适用于短期预测，灰色预测方法主要用于中长期预测［1］。

2.1.1 指数平滑法

指数平滑法是最常用的预测方法。其预测的基本原则是对未来的影响随历史数据越近而越大。另一条原则是根据预测误差来不断更正新的预测值。指数平滑法包括移动算术平均法、单指数平滑法。

（1）移动算术平均法优于传统的取时间序列的算术平均值作为预测值的方法，其优势在于时间序列的变化情况可以通过时间的推移来反映，对于平稳的短期预测有较好的精度，一般用于日用水量的预测。移动算术平均法计算简单，但须要庞大的基础资料，且仅适用于用水量变化较平稳的短期预测。其表达式如式（1）：

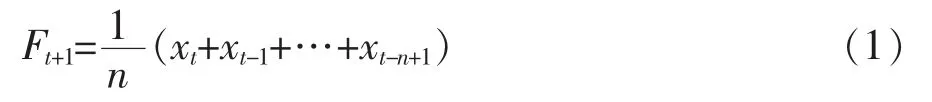
式中 t为当前时期；xt+xt-1+…+xt-n+1为稳定的时间序列观测值；n为所采用观测值的个数；Ft+1为t+1时期的预测值。

（2）单指数平滑法是根据移动算术平均法推导而出，由于其计算方便且需要的基础资料较少而获得普遍应用。但同样仅适用于平稳的时间序列，单指数平滑法如式（2）：

2.1.2 自回归－移动平均模型

若时间序列观测值为x1，x2，…，xt，该序列的平均数为μ，则该时间序列的自回归模型的表达式为：

式中 xt为该时间序列在t时期的预测值；p为模型阶数；φ1，φ2，…，φp为模型的系数；et为估计误差。

该时间序列（x1，x2，…，xt）的移动平均模型为：

式中 xt为该时间序列在t时期的预测值；q为模型阶数；θ1，θ2，…，θp为模型的系数；et为估计误差。

将上述模型相结合就可以建立自回归-移动平均组合模型，其表达式为：

式中 xt为该时间序列在t时期的预测值；p为模型阶数；φ1，φ2，…，φp为模型的系数；et为估计误差。

2.1.3 灰色预测模型

灰色预测模型所需城市历史数据较少，应用于中长期用水量预测具有较好的效果。其中GM（1，1）模型是灰色模型的基础，其建立过程为：

将原始序列X（0）通过一次累加得到一次数列X（1），并对数列X（1）建立一介微分方程：

式中 a为发展系数；u为内生控制灰度。

记参数向量为：

按最小二乘法求得：

该一阶微分方程的解为X（1）的预测值：

进行一次累减逆运算求得X（0）的预测值为：

灰色预测方法预测系统在未来一段时间内的变化趋势是根据过去和现在所知及未知的信息所建立的，从过去延伸到将来的灰色预测模型来实现的。

2.2 供水管网模型

城市供水系统是具有庞大规模、用水变化随机性强等特点的复杂多目标网络系统［2］。供水管网模型能够模拟管网运行工况，是城市基础建设的重要方面。按建模方法可分为宏观水力模型和微观水力模型两类。

2.2.1 宏观水力模型

宏观水力模型是建立在管网流量符合比例符合的基础上，忽略管网内部参数，运用统计数学的方法建立输入量（供水压力及流量）与输出量（压力监测数据）的经验数学表达式，达到求解的目的。

宏观模型相比微观模型，具有计算简单，便于维护和掌握的优点。在计算机建模软件没有广泛应用于供水系统时，宏观模型在实际工程中得到了广泛的应用。 美国的Demoyer［3］于1975年定义了一种比例负荷供水宏观模型：

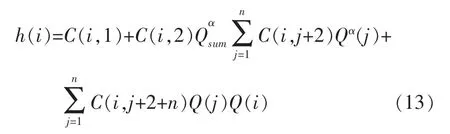
式中 h（i）为第i水厂供水压力；Qsum为此时段总用水量；C（i，j）为待定系数数组；n为管网中供水水厂的个数；Q（i），Q（j）分别为第i，j水厂供水流量；α为系数，取值范围一般为1.85～2。

2.2.2 微观水力模型

微观水力模型是利用管网信息并分析供水管网的拓扑结构，建立并求解连续性方程和能量方程组，从而获得供水管网中各个管段的流量、流速等管网全部运行参数，对管网改扩建及优化运行具有指导作用。

管网模型的求解方法随着对微观模型研究而日益增加，牛顿迭代法［4］就是最有效的方法之一。直接运用管网资料，从计算结果得出供水系统中各个节点和管段的运行信息，对供水管网的运行状态提供判断的依据，对供水管网的管理有指导性作用是微观模型最显著的优点，其缺点是所需要的基础资料较多，许多输入数据具有不确定性。

2.3 优化调度模型及求解

2.3.1 一般步骤

2.3.1.1 确定决策变量

决策变量是指系统输入所需的最少变量，一般指水泵台数、流量及出水压力。决策变量的确定是优化调度建模的基础。

2.3.1.2 确定目标函数和约束函数

目标函数是指运行达到指标的数学表达式。约束函数是指控制或制约系统运行变量的数学表达式。

通常优化调度的目标函数有以下几种：

（1）降低供水系统运行费用。制水成本及泵站能耗是供水系统运行费用的主要部分。其中绝大部分来自于供水泵站的能量消耗。在满足用户用水需求的条件下，利用电费峰谷平的特点，对调度周期内各个时段的供水量、水泵的开启及转速进行优化，达到供水泵站的节能降耗的目的，从而使整个供水管网系统处于低能耗的运行状态。取得经济效益的同时也降低了温室气体的排放，促进低碳社会的发展。

（2）减少管道漏失量。我国供水管网结构错综复杂，管网老龄化严重，管网漏失率一直居高不下，造成水资源和能源的浪费。漏失可能导致供水量和压力的不足，从而降低供水系统的可靠性和安全性，漏失还可能增加二次污染的风险。因此，如何降低供水管网漏失量是整个供水行业亟需解决的问题。

（3）降低维护保养费用。保持合理的供水压力，减少因管网压力过高造成爆管的可能性。在调度时，减少开停水泵的次数，避免设备加速磨损和水锤现象的出现。

2.3.1.3 确定约束条件

（1）满足最不利配水点对用水压力和流量要求。

（2）满足管网水力方程组的要求。

（3）各水厂在各时段供水能力的限制。

2.3.2 优化调度模型分类

2.3.2.1 直接优化调度模型

直接优化调度模型涵盖了泵站、管网和调节构筑物等复杂系统，在满足管网流量和压力需求的条件下，以运行费用最少为目标直接求得水泵的优化组合调度方案。因模型包含整个供水系统，造成模型过于复杂，求解方法少和计算困难等缺点。1992年，田一梅、赵新华等以供水的电费、制水成本、供水收入等为目标函数建立了城市配水系统直接寻优模型。

2.3.2.2 两级（间接）优化调度模型

在两级优化调度模型中，第一级优化是指以经济型最优、降低漏失、造价成本最低等为目标，以各送水泵站的供水流量和供水压力为限制条件，求得目标最优时各泵站不同时段优化后的流量和压力。第二级优化即在第一级优化的基础上，以满足泵站内安全性、经济性和高效性为原则，寻求各泵站内泵的最优组合［5］。供水规模较大，水泵运行组合数多的供水系统在进行优化调度时应使用两级优化调度模型。

2.3.3 优化算法的进展

国外对优化问题的研究起步较早，先后提出了动态规划、线性规划、非线性规划和混合整数规划、以及遗传算法等，并对其优缺点进行了比较，其中遗传算法颇受到研究人员的青睐。

遗传算法（简称GA）通过模拟在自然环境中生物的遗传与进化过程而产生的一种自适应全局优化概率搜索算法。遗传算法最早由Holland［6］教授在1962年首次提出，在20世纪80年代Goldberg对相关文献进行了归纳与总结，最终形成了遗传算法的基本框架。遗传算法是一种全局性优化算法，具有收敛性好，计算精度高，计算时间少，鲁棒性高等优点。目前，遗传算法已广泛应用于供水管网优化计算中，如水力水质模型的自动校核求解、管网供水的优化调度的求解等领域。Murphy，Simpson和Dandy等人于1993年首先在供水管网优化计算中使用遗传算法［7-8］。

3 结语

（1）随着计算机技术的普及及管网优化技术的提高，优化调度模型已成为越来越多的供水部门所采用的科学合理的方法对供水管网进行优化。

（2）建立管网模型可使供水管网运行状态得以体现，为管网优化提供支持，通过优化调度使之处于经济合理的运行状态。

（3）随着管网模型的普及及优化方法的改进与完善，供水管网优化模型必将受到人们的关注，得到更广泛的应用。

［1］赵洪宾.给水管网理论系统理论与分析［M］.北京：中国建筑工业出版社，2003.

［2］袁一星，高金良，赵洪宾，等.供水管网水力计算程序系统研究［J］.中国给水排水，1998，14（1）：27-28.

［3］DeMoyer， Robert， Jr.， Horwitz， Lawrence B.Macroscopic Distribution-System Modeling［J］.American Water Works Association， 1975，67（7）：377-384.

［4］许强，盛宁.城市给水系统优化调度研究综述［J］.南水北调与水利科技，2008（3）：115-117.

［5］曹平，郭召海，王燕，等.管网模型在多水源供水优化调度中的应用研究［J］.中国给水排水，2013，29（19）：49-53.

［6］王小平，曹立明.遗传算法—理论、应用与软件实现［M］.西安：西安交通大学出版社，2002.

［7］王荣和，姚仁忠，潘建华.遗传算法在给水管网现状分析中的应用［J］.给水排水，2000（9）：31-36.

［8］Goldberg D E.Genetic algorithms in search， optimization and machine learning ［M］.Addison-Wesley Publishing Co，Reading， Mass， 1989.

Research status of optimal operation of urban water supply network

LIN Ying-zi1，2，SONG Cheng-guo3
（1.Key Laboratory of Songliao Aquatic Environment，Ministry of Education，Jilin Architecture and Civil Engineering Institute，Changchun 130118，China；2.Laboratory of Urban Water Resource and Environment Restoration Engineering，Changchun 130118， China；3.School of Municipal and Environmental Engineering，Jilin Architecture and Civil Engineering Institute，Changchun 130118，China）

The main contents and research status of optimal scheduling， optimal modeling of water supply network and algorithm solution are briefly introduced.Optimal scheduling can ensure the safety and reliability of pipe network operation，and reduce the operation and maintenance cost of pipe network，so as to improve the social and economic benefits.

water supply network； demand forecasting； model； optimization scheduling

TV991.33 文献标识码：B 文章编号：1672-9900（2017）06-0011-04

2017-09-22

林英姿（1979-），女（汉族），吉林长春人，教授，博士，主要从事水资源与水环境修复工程方面的研究，（Tel）13844908048。

王艳肖）