电网畸变条件下的单相快速频率自适应锁频方案

贝太周，张博文

（1.国网山东省电力公司济南供电公司，山东 济南 250012；2.天津大学电气自动化与信息工程学院，天津 300072）

电网畸变条件下的单相快速频率自适应锁频方案

贝太周1，张博文2

（1.国网山东省电力公司济南供电公司，山东 济南 250012；2.天津大学电气自动化与信息工程学院，天津 300072）

分布式并网逆变器的同步控制和主动式孤岛检测需要电网基波频率的准确检测。为了提高在电网畸变环境下频率检测的准确性，基于单相分布式并网系统，提出一种能够在电网畸变条件下具有快速动态响应的频率自适应锁频方案。在该方案中，借助所提的改进型正交信号发生器和级联复数滤波网络分别实现直流分量和谐波扰动的有效消除和抑制。为保证所提方案在频率突变情形下仍然具有精准的性能，在αβ坐标系下构造了具有快速动态响应的频率自适应控制器，实现对电网基波频率的快速跟踪。方案的可行性通过仿真及实验结果得到验证。

电网同步；并网逆变器；谐波抑制；复数滤波器；频率自适应控制

0 引言

可再生能源具有更加清洁、更加可靠和产能灵活等突出优势［1-2］，依托可再生能源建立发展起来的分布式发电已经高比例渗透到传统的电力网络。作为分布式发电系统和电力网络之间的接口，电力电子设备、信息通信等技术将会在未来的电力网络中被广泛采用。电力电子设备的不断渗透引起人们对交流电能质量和电网稳定性的密切关注［2］。为了保证电力网络的高效稳定运行，应务必对分布式发电系统中的并网逆变器给予精心设计和精确控制。

为了保证并网逆变器能够向电网输送高质量的交流电能，就需要为其配置强劲稳健的技术支持。其中涉及并网逆变器控制的一个关键技术便是同步锁频技术。通过该技术获取的电网频率信息，可以用于并网逆变器的同步控制和主动式孤岛检测，一旦无法获取准确的电网频率信息，将会危及分布式发电系统的安全运行。实际应用中，常因电网暂态故障、电压测量及转换等原因引入一定量的直流分量［3］，同时真实电网环境中的谐波扰动［4］、频率突变［5］等情况均会阻碍电网频率信息的准确获取。

用于消除直流分量、抑制谐波扰动的电压同步技术在近期文献中被不断提出。在消除直流分量影响方面，均值误差补偿法［3］、积分反馈补偿法［6-7］以及dq坐标系下的交直流分量分离法［8］虽能有效消除直流分量，但是这些方法都是在传统结构的基础上通过引入其他结构单元来实现的，这在一定程度上增大了系统结构的复杂度和同步锁频的运算量。研究一种具有结构简单，可有效消除直流分量影响的同步锁频方案显得尤为重要。

在谐波抑制方面，借助复数滤波器进行多通道谐波解耦及补偿在近期文献中备受推崇［2，4，7］。 此种方法的核心在于对电网环境中存在较多的某次谐波分通道地进行无衰减提取，然后将提取到的谐波反馈补偿到电网电压采样信号中，即对某一谐波采用“先提取后补偿”的方式进行高效抑制。然而这类方法仅适用于谐波组成相对稳定的电网环境，当电网谐波畸变严重时，谐波抑制性能将大为受损。尽管可以通过添加通道数目的方法来加以改善，但是此种方法无疑又会增加系统实现的复杂度［9］。因此，如何保证滤波器能够在谐波畸变严重的电网环境下最大频率范围地抑制谐波是滤波器设计和实现时必须要考虑的问题。

本文将以单相系统的同步锁频技术为背景，首先提出一种兼具消除直流分量的新型正交信号发生器，然后基于复数滤波器构建了一种对各次谐波具有深度衰减作用的级联滤波网络。为了保证整个锁频系统能够在频率突变的电网环境中仍可以快速实现对电网频率的及时跟踪与锁定，在αβ坐标系下提出了一种不受电压波动影响的频率自适应控制器，文章最后对所提方案的可行性进行了仿真和实验验证。

1 可消除直流分量的改进型SOGI-QSG

图1所示的SOGI-QSG （Second Order Generalized Integrator based on Quadrature Signal Generator）方案易实现、运算量少［10-17］，因此在单相同步锁频方案中得到广泛应用。图中，k和ωo分别为SOGI-QSG的增益和中心频率。当中心频率ωo等于实际的电网基波频率ω时，SOGI-QSG可用于正交信号的产生［7］。

图1 SOGI-QSG结构

SOGI-QSG的特征传递函数为

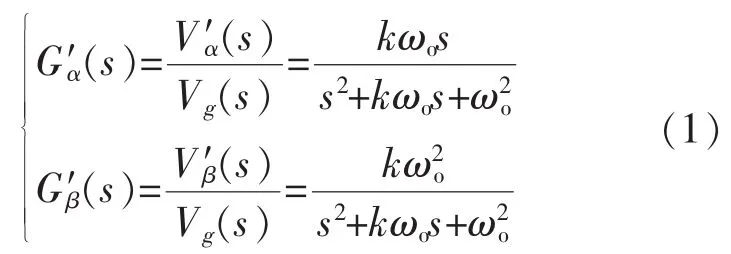
仅考虑直流分量影响，定义含有直流分量的电网电压vg为

式中：V、ω、vdc分别为电网电压的幅值、基波角频率和直流分量。

将式（2）中的直流分量vdc视为频率为0的交流量［8］，在稳态情况下（ωo=ω），SOGI-QSG 的输出为

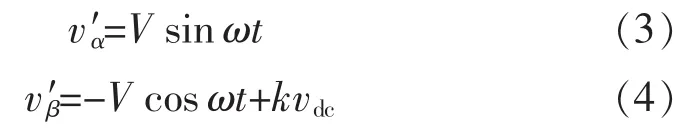
结合式（3）和式（4），当电网电压 vg混有直流分量时，SOGI-QSG 的输出电压 v′α和 v′β因 v′β内含有直流成分kvdc而无法严格正交，因此SOGI-QSG结构不具有消除直流分量的功能。针对这一不足，提出一种可消除直流分量的改进型SOGI-QSG。结合式（2）和式（3），稳态时，由 SOGI-QSG产生的电压分量 v′α可理解为式（2）中电网电压vg的交流分量，因此vg中的直流分量vdc在数值上又可表示为

将式（5）代入式（4），移项整理后得到

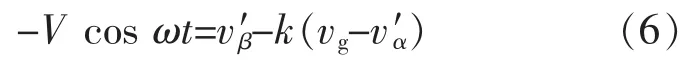
因此，若期望改进的SOGI-QSG在稳态时得到vα=V sin ωt及 vβ=V cos ωt的正交电压对，可令

基于图1和式（7）建立起的改进型SOGI-QSG结构如图2所示。

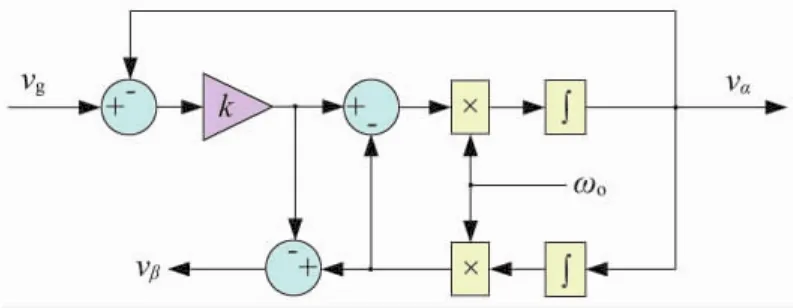
图2 改进型SOGI-QSG结构

相应的特征传递函数为

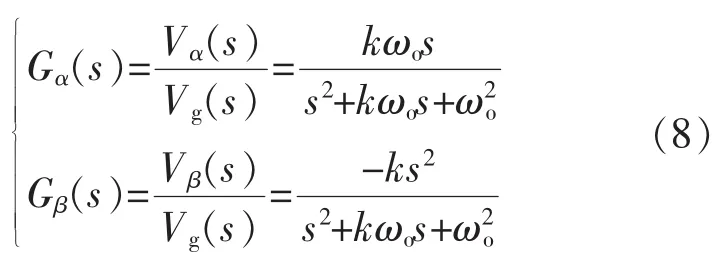
稳态时，式（2）所描述的电网电压vg经改进型SOGI-QSG后得到的任意时刻t时的电压输出为

为使 vα（t）中的 sinξ1ωt在实数范围内有意义，应满足0＜k＜2。在该范围内对k进行合理取值，即可保证 e-kωt／2在有限短的时间内快速收敛于 0， 此时vα（t）和 vβ（t）进一步简化为

式（10）表明，借助改进型SOGI-QSG可以得到一对严格正交的输出电压vα和vβ。另外，与SOGIQSG相比较，改进型SOGI-QSG并未添加辅助单元，因此改进方案具有结构简单、运算量少的显著优势。

关于k值的选定。k值同时影响着SOGI-QSG响应输出的调整时间和动态响应超调：当k取值较大时，调节时间缩短，超调量增大；当k取值较小时，调节时间延长，超调量减小；k取时可保证调整时间和动态响应超调之间关系最优［18］。

2 级联复数滤波网络

实际电网中的谐波扰动常常影响锁频性能［6］。为了保证锁频方案在谐波扰动下仍具有良好的性能，必须采取积极有效的措施来降低电网谐波的影响。

鉴于直流分量可在改进型SOGI-QSG内有效消除，故此处不对其予以分析。定义含有谐波扰动的电网电压vg为

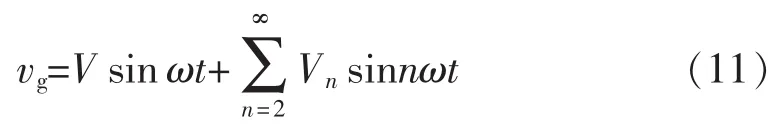
式中：n为谐波次数；Vn为n次谐波电压的幅值。

由式（8）可知，稳态时，改进型SOGI-QSG对自身输出电压vα和vβ中各次电网谐波的幅值和相位的影响用极坐标表示为

稳态时，式（11）所描述的电网电压vg经改进型SOGI-QSG后，得到的输出电压为

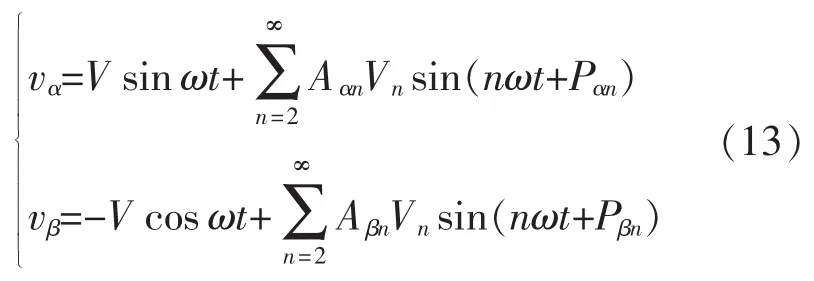
据式（13）可知，由于电网谐波的影响，电压分量vα和vβ中仍然含有相当量的各次谐波。为了保证锁频方案在谐波扰动条件下表现出良好的精度，应当最大限度地抑制vα和vβ中的各次谐波。

2.1 自适应复数滤波器

为了能够有效抑制电网谐波带来的影响，基于式（14）所描述的自适应复数滤波器（Adaptive Complex Filter，ACF）建立一种简单有效的滤波方案。

式中：m为ACF的增益；n为谐波次数；nωo构成了ACF对应于n次谐波时的中心频率。

在αβ坐标系下，复数因子j可通过交叉耦合方式实现［18］。因此，ACF的实现框图如图3所示。图中，vαi、vβi和 vαo、vβo分别为 ACF 的输入和输出。

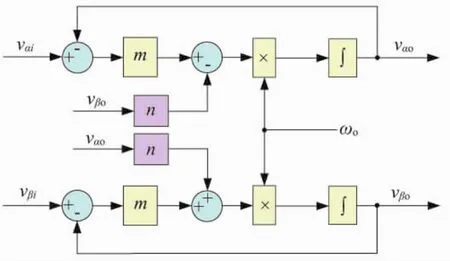
图3 ACF的实现

考查ACF的幅—相特性，其特性方程为

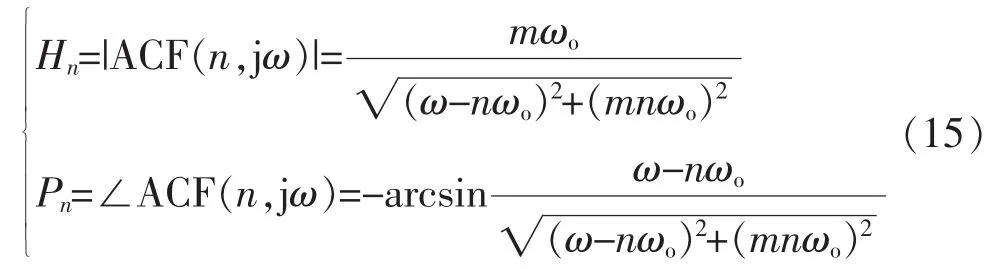
当 ωo=100π rad／s时，根据式（15），可以绘出ACF在（n，m）不同取值时的Bode图，如图4所示。根据该Bode图可知，n主要决定着ACF中心频率的位置，而m则影响着ACF带宽的宽度。

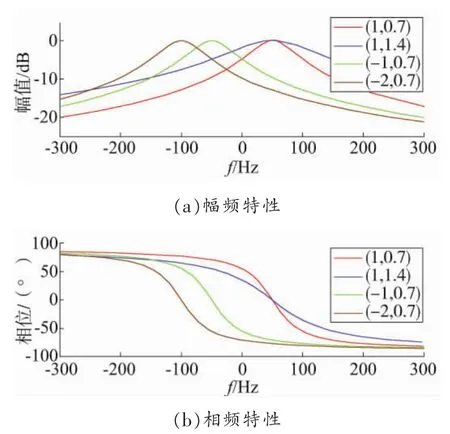
图4 （n，m）不同值时ACF的Bode图

观察图4发现，当n为负值时，ACF对电网中的各频率信号均有幅值衰减和相位偏移的影响，这种影响将随着负数n的减小而不断增强；而当n为正值时，ACF除了对自身的中心频率信号无任何影响外，对其他频率的信号将有不同程度的幅值衰减和相位偏移。特别地，当n取值为1时，借助某些控制策略，即可实现对电网基波频率的无差跟踪。

为分析简便起见，仅考虑ACF在n=±1时构成的级联滤波网络（Cascaded Filtering Network，CFN），网络结构如图5所示。

图5 由ACFs构成的级联滤波网络

2.2 参数设定

根据图5所示的CFN，可知其传递函数为

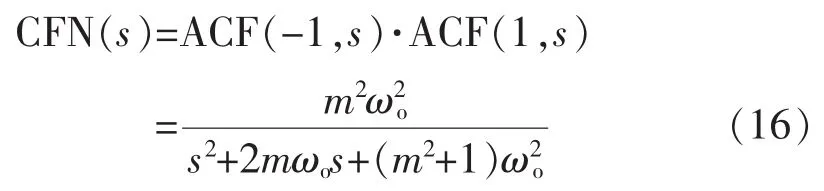
另外，由式（16）可知，增益m在数值上等于该二阶系统的阻尼比，因此，CFN单位阶跃响应的超调量为

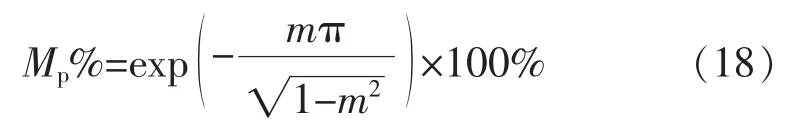
图6给出在ωo=100π rad／s以及不同m值情况下的式（16）所示的CFN的单位阶跃响应。

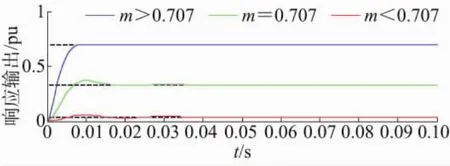
图6 不同m值情况下CFN的单位阶跃响应

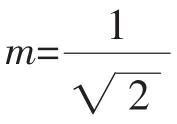
2.3 谐波抑制分析

稳态时，结合式（12）和式（15）中的 Hn以及已经确定的 k、m 值， 可以得到电压分量 vα1和 vβ1、vα2和vβ2中n次谐波的幅值衰减系数，分别如式（19）和式（20）所示。

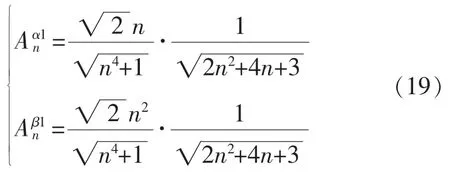
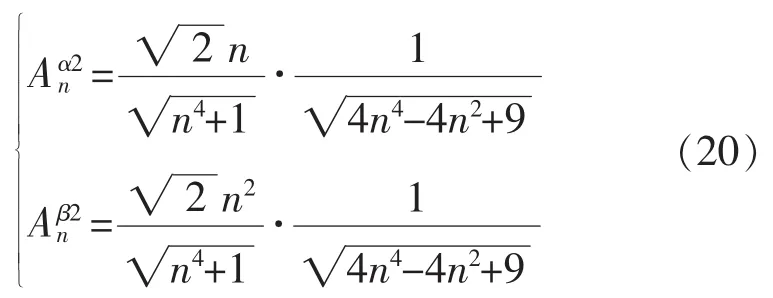
基于式（19）和式（20），图7给出了级联滤波网络对电压分量 vα1、vβ1和 vα2、vβ2中各次谐波的幅值衰减系数分布。

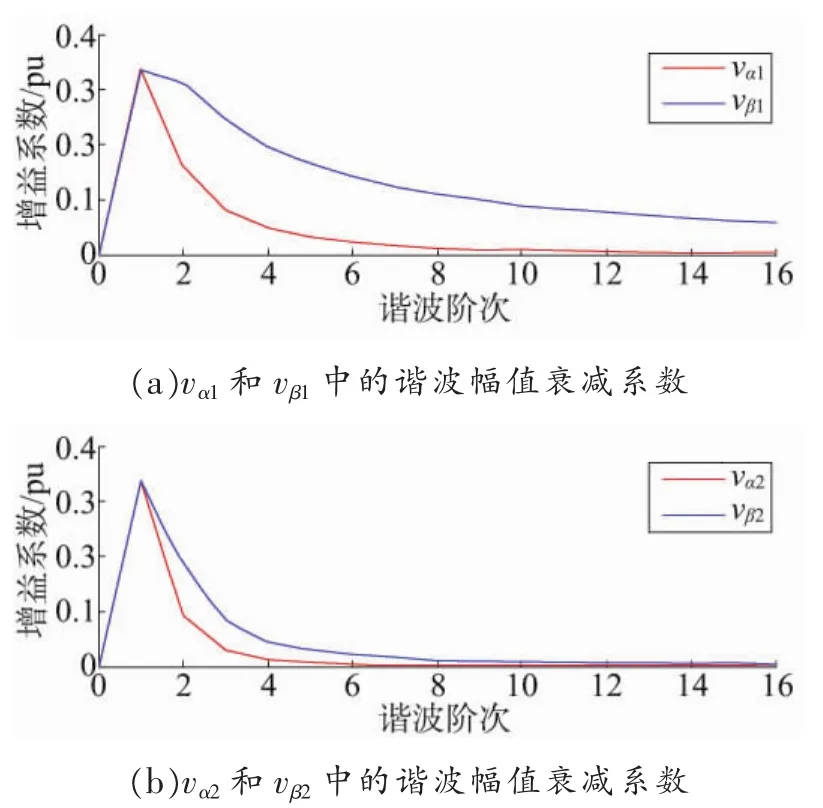
图7 CFN对谐波的抑制

观察图7可以发现，基于式（14）所示的自适应复数滤波器 ACF（-1，s）和 ACF（1，s）均可以为 vα1、vβ1和 vα2、vβ2中的各次谐波提供不同程度的幅值衰减系数，并且谐波的次数越高，提供的幅值衰减系数越小。

EN50160标准对公共配电系统中的电压质量做出了相关规定。按照此标准，电网中的各次谐波分量不能超出最大容许限值。考虑本文所提方案对电网电压中的各次谐波有很好的抑制能力，而对基波分量的影响很小，因此在进行频率自适应控制器的设计时仅考虑基波分量。

3 具有快速动态响应的频率自适应控制器

根据前文所述，当中心频率ωo等于电网基波频率ω时，改进型SOGI-QSG以及级联滤波网络可以保证良好的动态响应和滤波性能，考虑到实际电网存在频率突变的情形，应务求对实际电网基波频率进行快速准确跟踪，并及时调整中心频率，使两者趋于一致。

图5中，由改进型SOGI-QSG产生的电压分量vα和 vβ依次经过 ACF（-1，s）和 ACF（1，s）滤波后，输出电压 vα1、vβ1和 vα2、vβ2，分别表示为

设计频率自适应控制器的调整律为

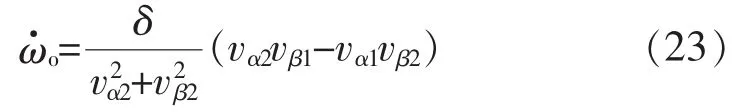
式中：δ为频率自适应调整系数。

将式（21）、式（22）同时代入式（23），可以得到

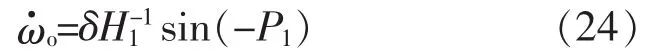
由于式（24）中不含H-1及P-1，因此，在整个锁频方案中，ACF（-1，s）仅起到滤波的作用，而对频率自适应控制器的调整律没有任何影响。特别地，当中心频率ωo无限接近于电网基波频率ω时，结合式（15）以及m的预设值，可将式（24）进一步化简为

频率自适应的动态调节过程可描述为：当ω＞ωo时，根据式（25）可及时调整 ωo线性增大；当 ω＜ωo时，可及时调整ωo线性减小；当ωo经过自适应调整等于ω时，ωo保持不变。因此，频率自适应调整律的实质在于：当电网基波频率ω改变时，迫使锁频输出ωo朝着消除这种改变的方向移动，直到ωo收敛于ω。

为了评估式（25）所描述的频率自适应调整的动态响应速度，定义用于检测频率响应的时间常数τ为

式（26）表明，在频率自适应调整系数δ一定的情况下，时间常数τ仅与电网频率ω成正比，而与电网幅值无关。因此，由式（23）确定的频率自适应调整律保证了整个锁频系统在频率调整的响应时间上不受实际电网中电压波动的影响。

按照电网接入标准的要求，分布式并网逆变器应在 47～52 Hz的频率范围内运行［17］，考虑到频率的小幅变化对频率自适应调整的动态响应速度和时间常数的影响十分有限，因此在借助式（26）确定频率自适应调整系数δ时，电网基波频率ω可取100π rad／s。

4 仿真及实验验证

为了验证本文所提的改进型SOGI-QSG的响应性能，将QSG的中心频率ωo设置为2π50 rad／s，输入信号选用20 V／50 Hz的交流信号混合1 V的直流偏置。输出电压的仿真结果如图8所示。观察图8可以发现，改进型SOGI-QSG经过20 ms的动态调整过程，稳定输出后电压分量vα和vβ中不再含有直流分量，vα和vβ严格正交。仿真结果显示了所提出的改进型SOGI-QSG结构可以简单有效地消除输入信号中的直流分量，快速构建正交电压。

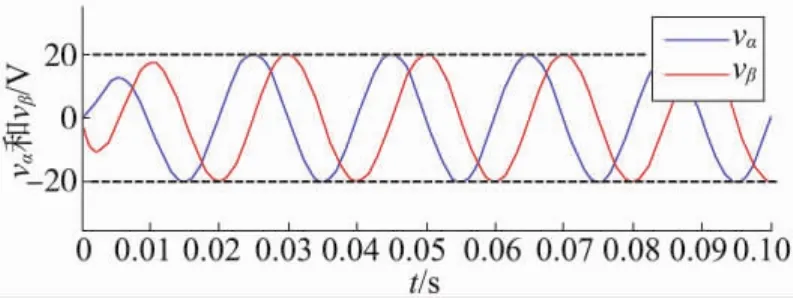
图8 改进型SOGI-QSG的响应

关于频率自适应调整律的验证，仿真中相关参数设置如下：用20 V／50 Hz的交流信号来模拟实际的电网电压，时间常数τ设置为20 ms，在t=0.04 s时刻，电网基波频率由50 Hz瞬间变为40 Hz。为了体现出该方案的动态响应性能，特将其与文献［19］中所研究的传统SOGI-FLL方案在同等条件下进行比较，所得的仿真结果如图9所示。据图9可以看出，当实际的电网频率发生突变时，采用本文所提方案，经过10 ms时间可以快速锁定当前的频率，而采用传统SOGI-FLL方案则需要40 ms。因此，所提方案具有更快的动态响应速度。

图9 频率自适应调整的动态响应

在实验室条件下，由可编程交流电源提供的幅值为20 V、频率为50 Hz的交流信号叠加1 V的直流偏置来模拟电网基波电压，QSG的电压增益k为。运算处理器芯片采用型号为TMS320F28335的DSP，采样频率为10 kHz。图10给出了采用改进型SOGI-QSG产生的正交电压vα和vβ的波形图。从波形图上能够看出：大约经过20 ms的调整，可以得到稳定的正交电压 vα与 vβ。 输出稳定后，vα与 vβ之间在相位上存在90°的相位差，而在幅值上，两者之间幅值相同，正负半周各自对称。

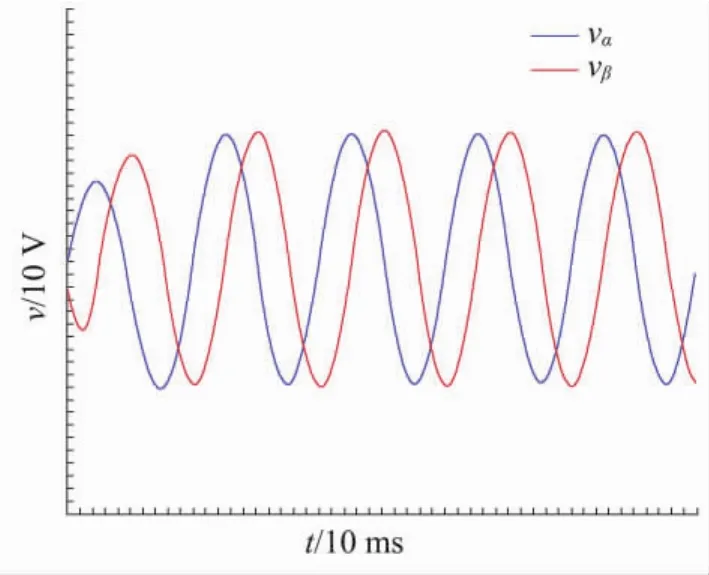
图10 正交电压实验波形

为了验证本文所提的频率自适应调整律的动态响应，初始输入信号中的基波分量采用幅值为20 V、频率为50 Hz的交流信号，谐波分量按表1取值。

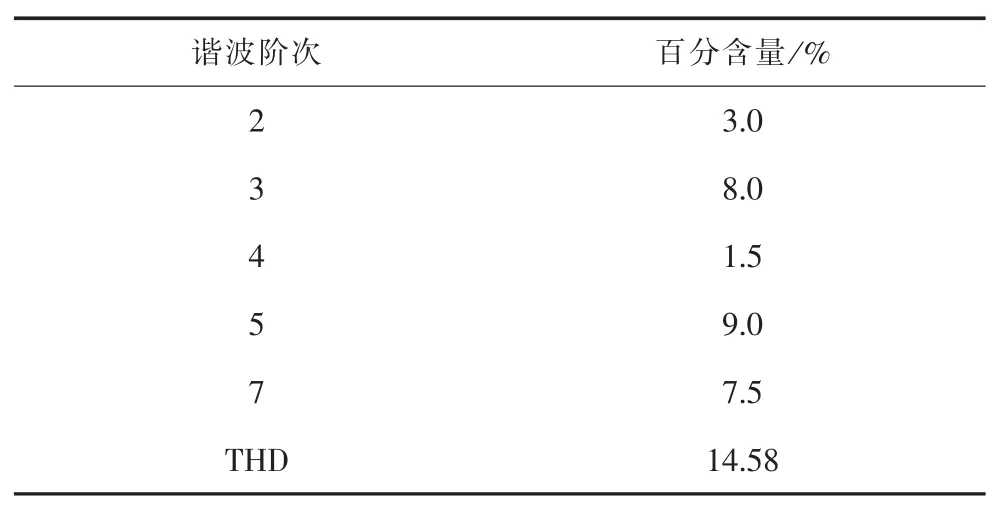
表1 谐波抑制测试中注入的谐波含量及THD

频率变化设定为由50 Hz突变到40 Hz。时间常数τ均设定为20 ms。为了验证幅值变化对锁频性能的影响，实验中设定两种幅值变化：幅值始终保持不变；在频率突变前幅值由20 V跌落为16 V。实验波形如图11所示。

由图11可知，当输入信号的频率减小时，若采用式（23）所示的频率自适应调整方案，无论输入电压是否发生波动，均不会对频率调整产生任何影响，在10 ms的时间范围内即可完成对频率的自适应调整与锁定。

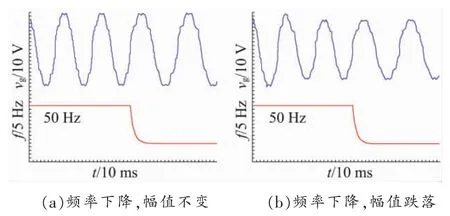
图11 频率变化时锁频方案的实验波形

5 结语

在考虑存在直流分量、谐波扰动和频率突变的电网畸变条件下，提出了一种可有效消除直流分量影响并抑制谐波畸变的单相频率自适应锁频方案。该方案能够有效消除直流分量和抑制电网谐波，同时快速的动态响应性能能够保证自身在较短的时间内快速锁定当前时刻的电网频率。总体方案具有结构简单、参数设置少、动态性能好等优点。可行性和有效性最后通过仿真和实验得以验证。

［1］VAZQUEZ S，SANCHEZ J A，REYES M R，et al.Adaptive vectorial filter for grid synchronization of power converters under unbalanced and／or distorted grid conditions［J］.IEEE Transactions on Industrial Electronics，2014，61（3）：1 355-1 367.

［2］MATAS J，CASTILLA M，MIRET J，et al.An adaptive prefiltering method to improve the speed／accuracy tradeoff of voltage sequence detection methods under adverse grid conditions［J］.IEEE Transactions on Industrial Electronics，2014，61（5）：2 139-2 151.

［3］HWANG S H，LIU L M，LI H，et al.DC offset error compensation for synchronous reference frame PLL in single-phase grid-connected converters［J］.IEEE Transactions on Power Electronics，2012，27（8）：3 467-3 471.

［4］杜雄，王国宁，孙鹏菊，等.两相静止坐标系下消除不对称和谐波影响的同步信号提取方法［J］.电工技术学报，2015，30（4）：249-256.

［5］汪飞，毛华龙，许德志，等.多变电网条件下的对称序列与谐波检测［J］.电工技术学报，2014，29（12）：158-165.

［6］王德玉，刘文钊，郭小强，等.非理想电网电压情况下并网变换器高阶解耦复数滤波并网同步技术［J］.中国电机工程学报，2015，35（10）：2 576-2 583.

［7］RODRIGUEZ P，LUNA A，CANDELA I，et al.Multiresonant frequency-locked loop for grid synchronization of power converters under distorted grid conditions［J］.IEEE Transactions on Industrial Electronics，2011，58（1）：127-138.

［8］杜雄，刘延东，孙鹏菊，等.消除直流分量影响的并网变流器同步参考坐标系锁相环方法［J］.电工技术学报，2013，28（12）：24-31.

［9］RODRIGUEZ P，LUNA A，MU OZ-AGUILAR R S，et al.A stationary reference frame grid synchronization system for threephase grid-connected power converters under adverse grid conditions［J］.IEEE Transactions on Power Electronics，2012，27（1）：99-112.

［10］THACKER T，BOROYEVICH D，BURGOS R，et al.Phase-locked loop noise reduction via phase detector implementation for singlephase systems［J］.IEEE Transactions on Industrial Electronics，2011，58（6）：2 482-2 490.

［11］REZA M S，CIOBOTARU M，AGELIDIS V G.Robust technique for accurate estimation of single-phase grid voltage fundamental frequency and amplitude［J］.IET Generation，Transmission&Distribution，2015，9（2）：183-192.

［12］辛振，赵仁德，郭宝玲，等.基于二阶广义积分器-锁频环的异步电机同步角频率估计方法［J］.电工技术学报，2014，29（1）：116-122.

［13］GHARTEMANI M K.A unifying approach to single-phase synchronous reference frame PLLs［J］.IEEE Transactions on Power Electronics，2013，28（10）：4 550-4 556.

［14］REZAM S，CIOBOTARU M，AGELIDIS V G.Accurate estimation of single-phase grid voltage parameters under distorted conditions［J］.IEEE Transactions on Power delivery，2014，29（3）：1 138-1 146.

［15］GHARTEMANI M K，KHAJEHODDIN S A，JAIN P K，et al.Addressing DC component in PLL and notch filter algorithms［J］.IEEE Transactions on Power Electronics，2012，27（1）：78-86.

［16］ELRAYYAH A，SOZER Y，ELBULUK M.Robust phase lockedloop algorithm for single phase utility interactive inverters［J］.IET Power Electronics，2014，7（5）：1 064-1 072.

［17］GOLESTAN S，MONFARED M，FREIJEDO F D，et al.Dynamics assessment of advanced single-phase PLL structures［J］.IEEE Transactions on Industrial Electronics，2013，60（6）：2 167-2 177.

［18］GOLESTAN S，MONFARED M，FREIJEDO F D，et al.Performance improvement of a pre-filtered synchronous reference frame PLL by using a PID-Type loop filter［J］.IEEE Transactions on Industrial Electronics，2014，61（7）：3 469-3 479.

［19］TUAN N，QUAN N，SANTOSO S.Improving performance of single-phase SOGI-FLL under dc-offset voltage condition［C］∥Proc.40th AnnualConf.IEEE IndustrialElectronics Society（IECON），2014：1 537-1 541.

Single-phase Fast Frequency Adaptive Frequency-locked Scheme under Distorted Grid Conditions

BEI Taizhou1，ZHANG Bowen2
（1.State Grid Jinan Power Supply Company，Jinan 250012，China；2.School of Electrical and Information Engineering，Tianjin University，Tianjin 300072，China）

Synchronous control and active islanding detection for the distributed grid-tied inverters need an accurate detection for the fundamental frequency of the grid.In order to obtain a high detection precision under the distorted grid conditions，based on the single-phase distributed grid-tied system，a frequency adaptive frequency-locked scheme is proposed with fast dynamic response performance.In the proposed scheme，the DC component and the harmonics are eliminated and rejected effectively by using the improved quadrature signal generator （QSG）and the cascaded complex filtering network presented in this paper，respectively.To ensure that the proposed scheme still has good performance under the frequency-varying situation，a frequency adaptive controller is built in the αβ-axes，for purpose of fast tracking the fundamental frequency of the grid.The feasibility of the scheme has been verified by simulation and experiment results.

grid synchronization；grid-tied inverters；harmonics rejection；complex filters；frequency adaptive control

TM76；TM46

A

1007－9904（2017）12－0016－07

2017-06-15

贝太周（1984），男，工程师，从事配电网运维与状态检修、主动配电网优化规划及分布式光伏并网系统运行与控制等工作。