对流层映射函数对精密单点定位的影响分析
2018-01-09翟树峰吕志平
翟树峰,吕志平,崔 阳,王 宁
(信息工程大学 地理空间信息学院,河南 郑州 450052)
对流层映射函数对精密单点定位的影响分析
翟树峰,吕志平,崔 阳,王 宁
(信息工程大学 地理空间信息学院,河南 郑州 450052)
分析对流层映射函数(NMF、VMF1和GMF)对精密单点定位(PPP)精度的影响,对分布于南北半球不同纬度地区的IGS跟踪站的观测数据进行解算。首先比较PPP坐标与IGS发布的日解SNX文件坐标差异和模型间PPP坐标差异,然后分析不同季节对模型差异的影响。实验结果表明,3种映射函数均可提高PPP精度,精度控制在1 cm左右。整体而言,VMF1和GMF对PPP精度的影响相当,且优于NMF。在不同季节里,模型差异会发生mm 级的变化。
IGS;精密单点定位;对流层延迟;映射函数;精度
PPP技术是一种利用GNSS接收机的双频码和载波相位观测值以及IGS等组织提供的高精度卫星星历和卫星钟差来进行单点定位的方法[1-2]。其定位精度可达厘米级。目前,在导航定位方面对PPP技术精度的研究仍是一个热点问题[2]。影响PPP定位精度的误差有很多,其中,对流层延迟是影响较为明显的一项误差。通常在天顶方向上,对流层延迟为2~3 m,但当卫星高度角降至10o左右时,对流层延迟会猛增至20~30 m[3]。目前,采用改正模型来削弱对流层延迟,即首先计算天顶方向对流层延迟,然后结合相应的映射函数将天顶方向的延迟映射到信号传播路径方向上[4]。采用PPP方法,本文利用3种对流层映射函数(NMF、VMF1和GMF)对若干IGS跟踪站的观测数据进行解算,并将3种映射函数下的解算结果作比较,分析了不同映射函数对PPP定位精度的影响。
1 对流层延迟模型
1.1 NMF映射函数
NMF模型是一种典型的经验模型,由Neill根据分布全球的26个探空气球站的观测资料建立[5]。该模型顾及了测站所在纬度和高程、观测时间以及对流层季节性变化等因素,忽略了气象元素气压P、水气压e和温度T,避免气象元素对模型的影响[6]。干延迟映射函数Md(θ)具体形式:

(1)
式中:第一项为平均项,第二项为波动项,θ为卫星高度角;ad,bd,cd为静力学常数,可根据参考文献[2]提供的内插公式和干分量投影函数系数表计算得到aht=2.53×10-5;bht=5.49×10-3;cht=1.14×10-3;H为正高。
湿延迟映射函数Mw(θ) 具体形式:
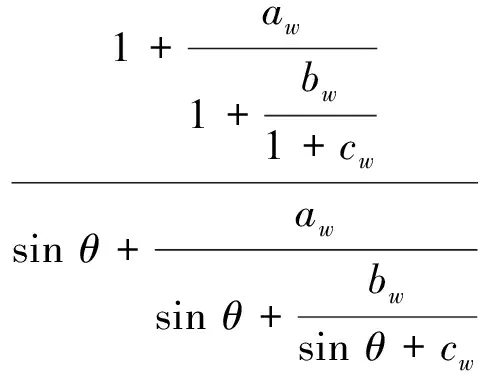
(2)
式中:θ为卫星高度角;aw,bw,cw为湿延迟映射系数,其计算方法也可参考文献[2]。
1.2 VMF1映射函数
VMF1模型是Boehm等人在VMF模型的基础上根据实测气象资料建立的一种模型[7-8],同NMF模型具有相似的形式。但模型中系数的求法区别于NMF模型。模型中系数和是由维也纳理工大学大地测量研究所基于实测的气象资料生成的以6 h为时间间隔的2.5°×2°的格网图给出,然后通过内插法得到测站的ad和aw的值[9]。系数bd和cd是根据欧洲中尺度天气预报中心(European Centre for Mediu-Range Weather Forecasts ,ECMWF)40年的观测资料得到的。其中,bd=0.002 9cd表示为纬度和年积日的函数,WMF1映射函数系数cd,具体形式:

(3)
式中:c0=0.062,而常数c11,c10,Ψ的取法在南北半球有所不同。在南半球,c11=0.007,c10=0.002,Ψ=π;在北半球,c11=0.005,c10=0.001,Ψ=0,bw=0.001 46,cw=0.043 91。采用VMF1模型进行精密单点定位的精度虽高,但基于实测气象资料得到的系数带有约34 h的延迟,实时性不够强[10]。
1.3 GMF映射函数
GMF模型也是一种经验模型,是Boehm等人为了解决VMF1模型实时性差的问题而建立的[11]。该模型中保留了VMF1模型中的系数b和c,而对于系数ad和aw,则是借鉴NMF中计算系数的做法,将其表示成测站经纬度(φ,λ)和年积日DOY的函数的形式,采用类似VMF1的射线追踪法计算得到。这样不仅消除实测气象资料造成的延迟,而且还简化计算过程,提高模型实时处理的能力。
1.4 映射函数模型分析
以上3种映射函数模型均采用三项连分式的形式,区别在于模型中系数的计算方法。系数的准确性直接影响到模型的精度,进而影响定位精度。因此,采用适当地映射函数模型对提高定位精度十分重要。
NMF是基于仅分布在北半球的少数探空站一年的观测数据来确定模型系数的,不具有全球覆盖性,而且随着NMF的发展,其缺陷也越来越明显:①依赖于纬度的偏差,在南半球高纬度地区偏差最大;②缺少对测站经度的敏感性,在我国东北和日本等地区,会产生测站坐标系统偏差。而基于ECMWF提供的观测资料构建的近实时的映射函数VMF1和GMF则弥补了NMF的不足。ECMWF 可近实时提供高时空分辨率的对流层折射率分布,所以VMF1和GMF分别利用不同的近实时的全球观测资料,采用射线追踪法计算系数ad和aw的值来提高模型精度。系数bd和cd采用ECMWF 40年的观测资料计算得到,其准确性要高于NMF。通过比较和分析3种映射函数模型系数的确定方法,可以得出:映射函数VMF1和GMF有利于提高定位精度,且在全球范围内适用,可以满足全球高精度GNSS数据处理的需求;NMF精度虽不及VMF1和GMF,但对于北半球中纬度地区,定位精度仍可得到保障。
2 映射函数对PPP的影响分析
选取分布于南北半球高中低纬度的34个IGS跟踪站在2013年第1天(采样率30 s)的观测数据作为实验数据进行精密单点定位,采用IGS分析中心发布的精密星历和精密钟差产品进行轨道和卫星钟差改正,参数与模型设置如表1所示。数据处理软件选用课题组自主研发的GNSS数据处理软件Gnsser[12]。分别加载NMF、GMF和VMF1等3种映射函数模型进行PPP解算,比较了PPP坐标与IGS发布的日解SNX文件坐标差异和模型间PPP坐标差异,最后分析不同季节对模型差异影响。

表1 参数与模型设置
2.1 PPP坐标与IGS真值坐标的比较
在3种映射函数模型下分别对观测数据进行PPP解算,然后利用IGS提供的SINEX文件的测站坐标(视为真值),将3种模型下解算的直角坐标(X,Y,Z)转换为站心坐标(N,E,U),最后通过站心坐标对3种模型进行比较,比较结果见图1—图3。

图1 NMF模型下PPP坐标与IGS真值坐标的比较
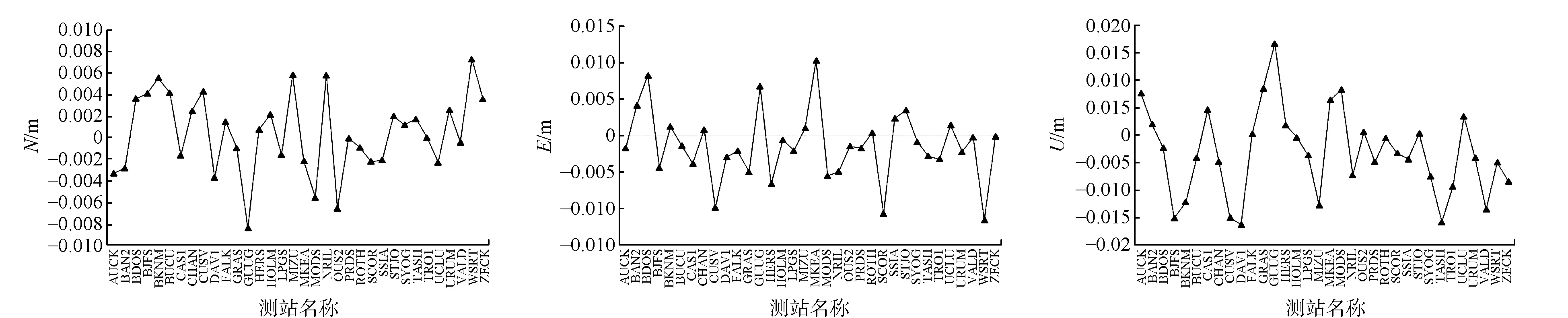
图2 GMF模型下PPP坐标与IGS真值坐标的比较

图3 VMF1模型下PPP坐标与IGS真值坐标的比较
从图中可以看出,在E和N方向上,PPP坐标与IGS真值坐标的差值基本上均在1 cm内,可见3种模型对PPP精度的影响相当。在U方向上,GMF和VMF1下的PPP坐标与IGS真值坐标的差值均不超过2 cm,且小于NMF下PPP坐标与IGS真值坐标的差值。表2给出了3种模型下所有测站的均方差。从表中可以看出,3种模型在E和N方向上的均方差几乎相同,而在U方向上,GMF和VMF1的均方差相近,且均比NMF小了近3 mm。由此可以得出,GMF和VMF1对PPP精度的影响差别不大,且均优于NMF。
为了进一步比较3种模型的差异性,利用PPP坐标与IGS真值坐标差值,计算了34个测站的PPP坐标3D偏差,结果如图4所示。
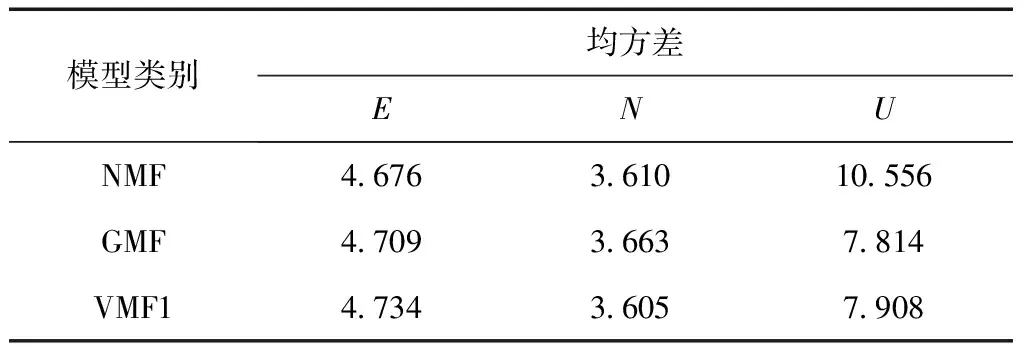
表2 不同模型下所有测站的均方差 mm

图4 不同模型下各测站PPP坐标3D偏差的比较
从图4可以看出,在NMF中,各测站的坐标3D偏差均在4 cm以内。而在GMF和VMF1中,各测站的坐标3D偏差均在2 cm以内。显然,GMF和VMF1的精度相近,且均优于NMF。
2.2 不同模型下PPP坐标的比较
将采用3种映射函数解算的PPP坐标比较,通过坐标差值更直观地看出模型间的差异。如图5—图7分别给出了3种模型相应PPP坐标的比较结果。
从图5和6可以看出,在Z方向上,NMF和GMF的差值与NMF和VMF1的差值均在2 cm以内。对于南半球高纬度地区的4个站(CAS1、DAV1、ROTH和SYOG),模型的差异尤为明显。鉴于NMF模型顾及了高程因素而忽略了气象因素,分析造成这种结果的原因与南半球高纬度地区的气候条件有关。在X和Y方向上,模型的差值均在1 cm内。而从图7看出,因GMF和VMF1均考虑气象因素,在各个方向上二者的差值均在8 mm以内。因此,在Z方向上,GMF和VMF1的精度更接近。在X和Y方向上,3种模型的差异不大。但综合来看,GMF和VMF1的精度要高于NMF。
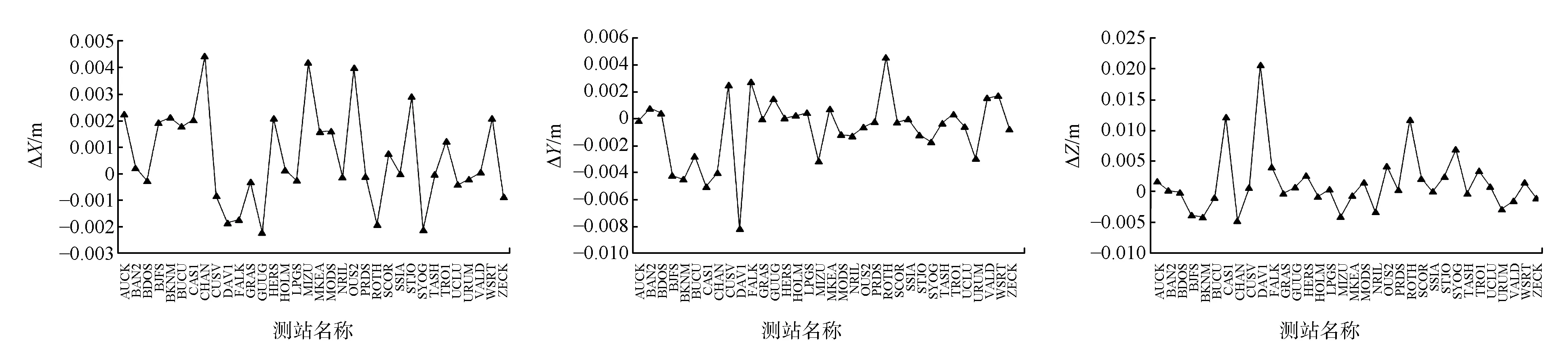
图5 NMF与GMF下的PPP坐标的比较

图6 NMF与VMF1下的PPP坐标的比较

图7 GMF与VMF1下的PPP坐标的比较
2.3 季节对模型差异的影响
文献[11]中提到,在我国东北和日本地区的1月份,NMF和GMF的差异造成的高程差异较为明显,最高达到10 mm,并且高程差异在全年范围内发生变化。NMF和VMF1的差异造成的高程差异也同样如此。为了分析引起上述变化的原因,本文选择该地区(区域内IGS站分布较少)的6个测站(BJNM、BJFS、CHAN、MIZU、SYYK和STK2),分别对6个测站2013年全年观测数据进行了解算。经验法则[13]表明,在高度角降至5°时,高程误差近似等于对流层延迟误差的1/5。鉴于高程变化更具直观性,可根据经验法则将映射函数差异转换为等价的高程差异[11],通过高程差异来间接地反映映射函数差异。图8—图13给出了6个测站的高程在3种模型间的差异的变化曲线。图中曲线中断部分表示IGS提供的数据缺失,相应年积日的高程差异没有画出。

图8 BJNM站在3种模型间的高程差异

图9 BJFS站在3种模型间的高程差异

图10 CHAN站在3种模型间的高程差异
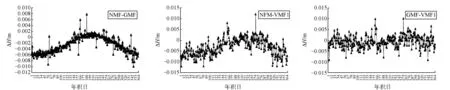
图11 STK2站在3种模型间的高程差异

图12 SYYK站在3种模型间的高程差异

图13 MIZU站在3种模型间的高程差异
从图8—图13可以看出,NMF关于GMF的高程差异在全年范围内随时间变化呈余弦曲线分布。在2—12月,高程差异基本上均超过5 mm,最高达到15 mm(BJNM站)。在5—8月,高程差异基本上在4 mm以内,最高达到10 mm(BJNM站)。NMF关于VMF1的高程差异在全年范围内分布相对离散,但仍大致呈余弦曲线。在2—12月,除了SYYK站,高程差异基本上在10 mm以内,最高误差达到17 mm(MIZU站)。在5—8月,高程差异基本上在5 mm以内,最高达到13 mm(STK2站)。GMF关于VMF1的高程差异在全年范围内分布离散,但没有出现明显的波动,高程差异基本在10 mm以内,可见GMF和VMF1的一致性相对较好。我国东北和日本地区在2—12月和5—8月期间分别处在冬季和夏季,从上述分析可得出:NMF和GMF的差异与NMF和VMF1的差异随季节的更替而有规律地变化,且较为明显,而GMF和VMF1的差异随季节的更替没有明显的变化。
3 结束语
对流层延迟是对PPP定位精度影响较为明显的一项误差。本文介绍了GPS数据处理中常用的3种对流层延迟映射函数,对分布于南北半球不同纬度地区的34个IGS跟踪站的单日观测数据和部分站的全年数据,采用不同的映射函数进行解算。比较分析3种映射函数对PPP精度的影响。实验结果如下:
1)在南北半球不同纬度地区,除了个别测站,3种模型差异不大,精度均在1 cm左右。整体而言,GMF和VMF1对PPP精度影响相当,且较NMF略好。
2)在我国东北和日本地区,模型差异会随季节的改变而发生mm级的变化。这是因为NMF确定系数时采用的探空数据不覆盖中国及附近区域,而GMF和VMF1在确定系数时采用的是ECMWF提供近实时的全球观测资料。
[1] 赵兴旺,王胜利,刘超. GNSS精密单点定位理论与方法[M]. 合肥:中国科学技术大学出版社,2015.
[2] 李征航,黄劲松. GPS测量与数据处理[M]. 武汉:武大出版社,2010.
[3] 李凯峰,欧阳永忠,陆秀平,等. 静态精密单点定位中对流层延迟估计[J]. 海洋测绘,2011, 31(6): 12-15.
[4] 李盼,李星星,王磊,等. 对流层湿延迟估计方法对PPP数据处理的影响[J]. 武汉大学学报(信息科学版),2010, 35(7): 850-853.
[5] NIELL A. Global mapping functions for the atmosphere delay at radio wavelengths[J]. Journal of Geophysical Research, 1996, 101(b1): 3227-3246.
[6] 李黎,匡翠林,朱建军,等. 水平梯度和映射函数对PPP对流层延迟估计的影响分析[J]. 工程勘察,2011,(5): 52-56.
[7] KOUBA J. Implementation and testing of the gridded Vienna Mapping Function 1(VMF1)[J]. Journal of Geodesy, 2008, 82: 193-205.
[8] BOEHM J, WERL B, SCHUH H. Troposphere mapping functions for GPS and VLBI from ECMWF operational analysis data[J]. Journal of Geophysical Research, 2006, 111, B02406, doi: 10.1029/2005JB003629.
[9] 王君刚,陈俊平,王解先. GNSS对流层延迟映射模型分析[J]. 天文学进展,2014, 32(3): 383-394.
[10] 张双成,叶世榕,刘经南,等. 动态映射函数最新进展及其在GNSS 遥感水汽中的应用研究[J]. 武汉大学学报(信息科学版),2009, 34 (3) : 280-283.
[11] BOEHM J, NIELL A, TREGONING P, et al. Global Mapping Function (GMF): A new empirical mapping function based on data from numerical weather model data [J]. Geophysical Research Letters, 2006, 33, L07304, doi: 10.1029/2005GL025546.
[12] 陈正生. 大规模GNSS测量数据分布式计算关键技术研究[D]. 郑州:信息工程大学, 2014.
[13] MACMILLAN D, MA C. Evaluation of very long baseline interferometry atmospheric modeling improvements [J]. Journal of Geophysical Research, 1994, 99(B1): 637-651.
Influenceanalysisoftroposphericmappingfunctionsonprecisepointpositioning
ZHAI Shufeng, LU Zhiping, CUI Yang, WANG Ning
(School of Geospatial Information, Information Engineering University, Zhengzhou 450002, China)
Observations of IGS stations in different latitude areas in north and south hemisphere are computed in order to analyze the influence of tropospheric mapping functions on Precise Point Positioning (PPP). Differences of PPP coordinates and daily SNX file coordinates issued by IGS and PPP coordinates between models are compared. Finally, the influence on the difference between models by seasons are analyzed. The result shows that three mapping functions can improve the PPP precision, in which the difference is small, GMF and VMF1 have the similar influence on the PPP precision, and both are better than NMF. In different seasons, the difference between models will change in the form of mm.
IGS;PPP(precise point positioning); tropospheric delay; mapping function; precision
著录:翟树峰,吕志平,崔阳,等.对流层映射函数对精密单点定位的影响分析[J].测绘工程,2018,27(1):24-30.
10.19349/j.cnki.issn1006-7949.2018.01.006
2016-10-31
国家自然科学基金资助项目(41674019);国家重点研发计划(2016YFB0501701)
翟树峰(1990-),男,硕士研究生.
吕志平(1960-),男,教授,博士.
P228
A
1006-7949(2018)01-0024-07
李铭娜]
