我国股指期货与现货市场的已实现波动关系研究——基于非参数Tn非线性Granger因果关系检验

高 爽，王联欣

(天津大学 管理与经济学部， 天津 300072)

我国股指期货与现货市场的已实现波动关系研究
——基于非参数Tn非线性Granger因果关系检验

高 爽，王联欣

(天津大学 管理与经济学部， 天津 300072)

沪深300股指期货与股票现货之间的波动关系近年来受到学者的广泛关注。首先使用5 min高频数据计算了沪深300股指期货与股票指数的已实现波动率序列，发现二者之间高度相关，之后以两个实现波动序列为研究对象，运用线性和非线性Granger因果关系检验方法，对二者之间的线性及非线性波动关系进行实证研究。结果表明：我国股票现货的波动会显著引起股票期货的波动，而股票期货的波动不会对股票现货的波动造成显著影响。

股指期货; 已实现波动; 非线性Granger因果关系

众所周知，期货是全球金融市场重要的衍生工具之一，因其套期保值、价格发现等功能，使其成为投资者规避风险、实现资产保值的重要金融工具。随着我国金融市场环境逐渐成熟，在2010年4月16日，沪深300股指期货正式挂牌交易。由于我国金融市场环境尚不成熟，制度仍不完善，导致我国的股指期货对沪深300股指的影响关系与国外成熟市场不同。基于该问题，本文拟对我国沪深300股指期货对于沪深300指数的波动性影响进行深入研究。

谈到对金融资产波动性进行研究，离不开波动率的测度方法。按照应用与计算方式的不同，可以将波动率划分为隐含波动率、历史波动率和“已实现”波动率。在20世纪90年代之前，学术界与实务界对于波动率的测度仅采用低频数据，即抽样频率为年、季度、月、周、日的时间序列，如隐含波动率和历史波动率都是基于低频数据的波动率测度方法。20世纪90年代之后，Bollerslev与Andersen提出了基于金融高频数据的“已实现”波动率[1-2]，从此开启了金融界研究金融高频数据的大门。高频数据是指抽样频率为小时、分、秒的时间序列，它可以更加迅速地捕捉市场信息，比低频数据更能反映市场的真实情况。所以，本文采用已实现波动率方法来研究沪深300股指期货与沪深300指数之间的波动关系，以期发现两者之间更真实的波动溢出。

对于期现波动关系的研究，国外学者已形成了较多理论成果。1983年，Garbade等[3]曾以商品期货和现货的价格作为研究样本，通过建立动态模型，发现在价格发现功能中期货价格和现货价格作用的大小差异。随后Ross[4]通过研究1987年美国股市大崩盘期间标普500指数与期货之间的关系，发现在现货市场波动剧烈的情况下，股指期货的出现会加剧现货市场的波动性。但AntoniosAntoniou等[5]的研究则认为，推出股指期货并没有增加股票市场的波动性，而且与股票市场的波动性无关。2004年，Maosen Zhong等[6]以墨西哥IPC指数的日数据为研究对象，发现期货的价格发现功能在墨西哥股指期货交易中比较明显，而且确实能够加剧股票市场的波动性。Li[7]在用马尔科夫向量误差修正模型研究期现货市场的动态关系时也发现了期货价格引导现货价格，而现货价格无法引导现货价格的现象。由以上可以看出：国外学者对于现货之间的关系观点还没有达成一致，这主要是因为学者们研究的样本不相同，各个国家的期货现货关系肯定不一致； 同时研究方法也不相同，这些都会导致结果的差异。

我国在期货与现货之间的波动性研究方面起步较晚，严敏、邢精平等[8-9]对沪深300期货与现货之间波动溢出关系进行了研究，发现我国的股指期货市场和股票指数市场间存在长期协整关系，且短期内会相互影响。

国际与国内的学者对期、现货关系的研究主要限于低频领域的线性协整关系研究，还没有学者对两者的高频波动关系进行过非线性研究。本文首次采用“已实现”波动率来度量期现之间的波动，并首次采用非参数Tn进行非线性granger因果检验的方法来检验两者“已实现”波动之间的非线性关系。

综上可见，多数学者在对股指期货和股票指数的波动关系进行研究时采用的是低频数据，且在研究中常使用线性granger因果关系检验。Granger[10]曾指出：“世界几乎肯定是由非线性关系构成的”。当我们忽略变量之间可能存在的非线性关系，采用传统的线性granger因果检验来检验变量间关系时，可能会造成显著偏差。同时，低频数据忽略了大量市场信息，相对于高频数据而言所覆盖的信息量较少，而高频数据可以迅速反映市场信息，能够更加准确地反应市场真实情况。另外，根据李胜歌等[11]对深证成指最优抽样频率的研究结果，5 min抽样频率能够在噪声条件下得到波动的较精确估计。因此，为了更准确地反映我国沪深300股指期货和沪深300指数之间的波动关系，本文采用5 min高频交易数据，通过基于高频数据的波动估计量来度量股指期货和现货市场的波动情况，并首次使用最新研究发现的非参数Tn非线性granger因果关系检验来分析股指期货与现货市场之间的波动关系。

1 研究方法与理论模型

1.1 基于高频数据的“已实现”波动率

近年来，由于国外衍生品市场的活跃，迫切需要从高频波动中挖掘隐含的信息。计算机技术的发展也为高频数据的获取与分析提供了可能。对高频时间序列的波动度量方法，大多学者与投资人采用“已实现”波动率(realized volatility，RV)的方法。它使用一定时间间隔的收益率的平方和来估计每日的收益率的方差[1-2],它没有模型，因此不需要进行复杂的参数估计，这也是它与ARCH类模型与SV类模型的显著区别。此外，相对于历史波动率、隐含波动率(基于低频数据)而言，“已实现”波动率能尽可能地反映全部日内信息，波动的估计更加准确。

设

rt,n=pt,n-pt,n-1

t=1,2,…,T;n=1,2,…,N

(1)

其中:pt,n为金融资产在第t日内的第n个对数价格;rt,n为金融资产的日内对数价格收益;N为在[t-1,t]时间段内等时间间隔的取样次数。

根据Anderson等[1]定义，“已实现”波动为金融资产的日内收益平方之和，数学表达式为：

(2)

1.2 BDS非线性关系检验

非线性检验方法主要包括Bispectral检验、BDS检验、RESET检验、F检验、Mcleod-Li检验几类。其中BDS检验是非线性检验的常用方法。BDS检验与其他检验方法的区别在于，它可以提供简洁证据证明存在非线性关系，而不能直接提供非线性检验。以下简要介绍一下BDS检验的基本原理。

1996年，受到“相关性积分”的启发，Brock等[12]提出了BDS非线性检验的方法，该方法可考察变量之间是否存在非线性的关系。任取序列yt，定义Cm(ε)如下：

Cm(ε)=n-2[配对(i,j)的个数，其中配对(i,j)满足：yi-yj|<ε,|yi+1-yj+1|<ε,…,|yi+m-1-yj+m-1|<ε]

因此，yi,…,yi+m-1与yj,…,yj+m-1分别为序列中长度为m的片段，且对应点距离为ε，基于Cm(ε)，Brock等提出了BDS检验统计量，并对原假设 “序列是独立同分布的”进行检验：

BDS=n1/2[Cm(ε)-C1(ε)m]

1.3 Granger因果关系检验

1) 传统的线性Granger因果关系检验方法

1969年，Granger提出了Granger因果关系检验方法[13]，该方法应用于宏观经济的各个方面，成为金融理论研究应用较广泛的计量工具。该方法假定取得的时间序列{Xt,Yt,t≥1}是严格平稳的，若Xt过去及当期的观测值包含着Yt未来信息，则Xt是Yt的Granger因果原因。若令FX,t和FY,t分别表示包含t时期以前的Xt与Yt的观测值信息集，令“～”表示等价，当Xt不是Yt的Granger原因，即Xt过去及当期的观测值并没有包含着关于Yt未来观测值的“有用”信息时，对于任意的k≥1，以下关系式成立[14]：

(Yt+1,…,Yt+k)|(FX,t,FY,t)～

(Yt+1,…,Yt+k)|FY,t

(3)

此外，线性Granger因果关系检验的前提条件是假设E(Yt+1|(FX,t,FY,t))为参数的、线性的时间序列模型[14]。

线性的Granger因果关系检验可以在Sims[15]提出的VAR模型框架下进行，也可以在VEC模型框架下进行。在此仅以VAR模型为例。例如xt、yt分别代表VAR模型里的随机内生变量，具体表示为：

(4)

(5)

其中：{xt}、{yt}表示两个平稳时间序列；αj、βj、γj，j=1,2为待估参数。残差项为{εi,t}，j=1,2，并且{εi,t}～i.i.N(0,1)。m、n、p、q代表最大滞后阶数。在VAR模型框架下，通过考察自回归系数的联合显著性对变量间的线性Granger因果关系进行检验，即如果式(4)中γi,t=0，i=0,1,2,…,n的联合显著性检验原假设被拒绝，就意味着序列{yt}是{xt}的Granger原因。如果式(5)中βi,t=0，i=0,1,2,…,p的联合显著性检验原假设被拒绝，就意味着序列{xt}是{yt}的Granger原因。如果以上两个原假设同时被拒绝，则说明序列{xt}和{yt}之间存在着双向Granger因果关系[14]。

2) 非参数Tn非线性Granger因果关系检验方法

金融时间序列常常呈现出复杂的非线性动态变化趋势，因此常规的线性VAR模型难以全面、准确地描述经济变量之间的Granger因果关系，导致结果出现明显偏差，使结果不可靠。1992年，Baek等[16]提出了一种基于非参数统计量的检验方法，以此来检验非线性Granger因果关系。该方法为了检验变量之间的非线性Granger因果关系，采用积分原理的思想来估计跨时间的相关概率，不过该方法有个应用限制条件，即要求被检测残差序列之间必须是独立同分布的。1994年，Hiemstra等[18]修正了这个条件，允许被检测的残差序列之间存在弱相关性(HJ方法)，但HJ方法存在另一个问题，即在检测过程中会产生过度拒绝的现象。2006年，Diks等[19]利用非参数核密度估计的理论，提出了全新的非参数统计量，用来考察残差序列是否存在非线性Granger因果关系。通过调节频率范围，这种非参数检验方法可以自动考虑条件分布的变化，从而克服了HJ方法中过度拒绝的问题。这种方法解决了前两种方法的问题，从而使得出的结论更加可靠。

鉴于非线性Granger因果关系已经可以对变量之间的非线性关系进行有效描述，并能够摆脱线性假设下的模型失准问题，本文采用Diks和Panchenko提出的非线性非参数Granger因果关系进行检验。该理论把原假设重新表述为

(6)

2 实证方法与数据描述

2.1 样本选取

本文选取2010年12月16日—2013年3月15日沪深300指数与股指期货合约5 min交易数据共296×48=284 16个数据，数据来源于wind咨询金融数据终端。由于期货合约有交割期限，而通常的趋势是，临近交割期时期货现货价格基本趋于一致[20]，因此本文采用将交割日在次月的合约连接起来，制成连续合约，以此为样本数据进行研究。即利用IF1201，IF1202，…，IF1303合约构造出连续的期货价格的时间序列，并选取线同时间段的沪深300指数5 min收盘价格共同构成样本数据。由于沪深300股指期货的交易时间为上午9:15—11:30以及下午13:00—15:15，而股市的交易时间为上午9:30—11:30，13:00—15:00。因此，本文将股指期货交易每日前15 min、后15 min的5 min价格剔除，以保证期限价格数据的时间一致。本研究采用EVIEWS7.2、MATLAB2012a以及C语言对数据进行处理与计算，同时选取的时间区间，避开了2010年4月16日股指期货刚开始上市交易的阶段，防止早期期货市场的非理性交易等不成熟表现对最终结果造成影响。因此，该时间段的选取使得研究数据较真实，客观地反映该时间段的市场情况，使结果更加可靠。

2.2 实证结果分析

1) 基本描述统计

根据式(2)，本文求得了沪深300指数与沪深300股指期货两者的“已实现”波动率序列，并利用Eviews7.2做出其时间序列图(见图1、2)，并在表1中进一步列出了2个序列的基本描述统计数据。从表1可以看出：2011年12月16日到2013年3月15日之间两只“已实现”波动率序列峰值均高3，Jarque-Bera统计量的相伴概率基本为0，说明这两只序列不是正态分布，同时偏度均大于0，说明两只序列具有右偏的特点。

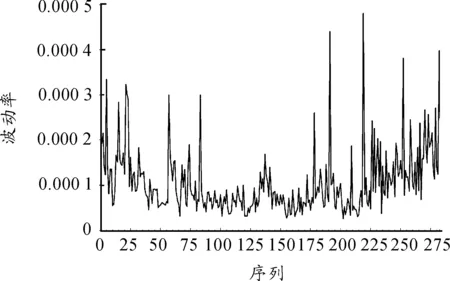
图1 沪深300指数“已实现”波动率序列图

均值最大值最小值标准差偏度峰度JB统计量概率沪深300指数8．68E-050．000581．23E-059．50E-052．0441428．197030513．7470．00股指期货8．44E-050．000482．57E-057．10E-052．1646839．048202650．0580．00

2) 单位根检验

利用对数收益率序列计算得到“已实现”波动率序列后，对变量的单整阶数进行检验来验证其是否平稳，以保证在后续非线性分析中采用正确的变量形式。本文采用传统的ADF检验方法，结果如表2所示。从表中可以看出：检验结果均小于1%显著水平临界值，显著地拒绝了“存在单位根”原假设，这说明“已实现”波动率序列是平稳的，因此以下将在“已实现”波动率序列为平稳序列的基础之上进行研究。

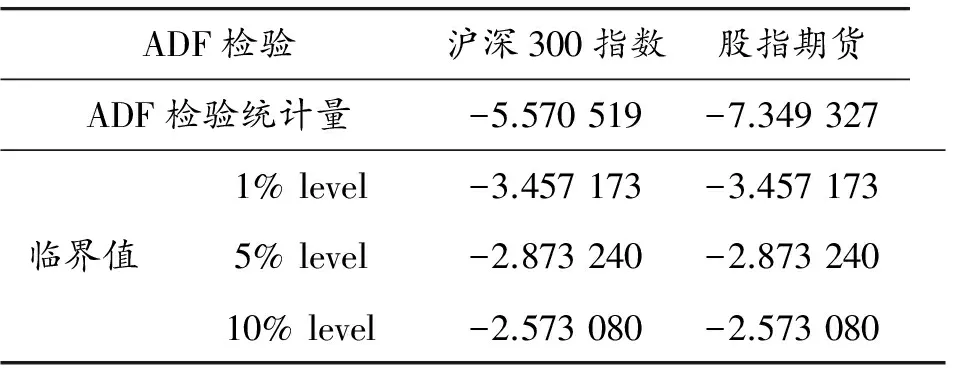
表2 沪深300指数“已实现”波动率序列与沪深300股指期货“已实现”波动率序列的ADF检验结果

3) 非线性检验

在对沪深300股指期货与股票市场之间的非线性因果关系开展研究之前，首先要进行非线性检验，以考察两者之前是否存在非线性的动态变化趋势。从20世纪80年代至今，产生了几种非线性检验的新方法与新技术，如Bispectral检验、BDS检验、RESET检验、F检验、Mcleod-Li检验，还有神经网络非线性检验等。但是，由于不能准确确定时间序列非线性的来源，因此对于哪种检验方法最好很难下定论。因此，本文采用BDS检验方法对两者的非线性的动态变化趋势进行检验。

在现有的部分研究中，如Hsien[21]、Mougou[22]均通过最优的VAR模型过滤处变量间的线性依存成分。在此基础上，分别对经线性过滤后的残差序列进行非线性检验。因此，本文也首先通过最优VAR模型对期货、现货的“已实现”波动序列相互影响关系进行估计，并过滤相互间的线性依存成分，在此基础上，对过滤出的两个残差序列进行BDS检验。结果如表3、4所示。

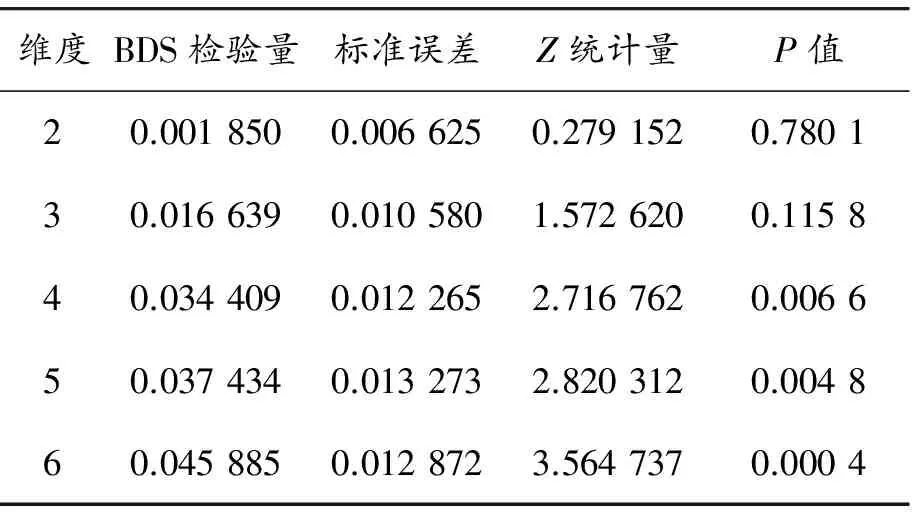
表3 基于VAR系统中沪深300指数的回归残差BDS检验结果

表4 基于VAR系统中沪深300股指期货的回归残差BDS检验结果

注：原假设为假设两序列独立同分布，ε=0.7σ； 维度指的是连续点的个数

由BDS结果可以看出：随着维度的(即连续点的个数)增加，P值逐渐降低并趋近于0，说明在经VAR模型线性过滤后的沪深300指数“已实现”波动率与股指期货“已实现”波动率的残差中，两者均拒绝独立同分布的原假设，说明两个残差序列存在显著的非线性关系。这为下一步进行非参数Tn的非线性granger 因果关系检验打下基础。

4) granger因果关系检验

为了比较线性与非线性granger因果关系检验在检验结果上的区别，分别用这两种方法对波动关系进行检验，并最终给出对比结果。由于滞后阶数的选择不同会直接影响Granger因果检验的结果，同时股票市场的信息流动的时效性比较强，短期的波动关系影响对投资分析具有直接意义，因此本文选取共同滞后阶数(lx=ly)1～8的检验结果列于表5。

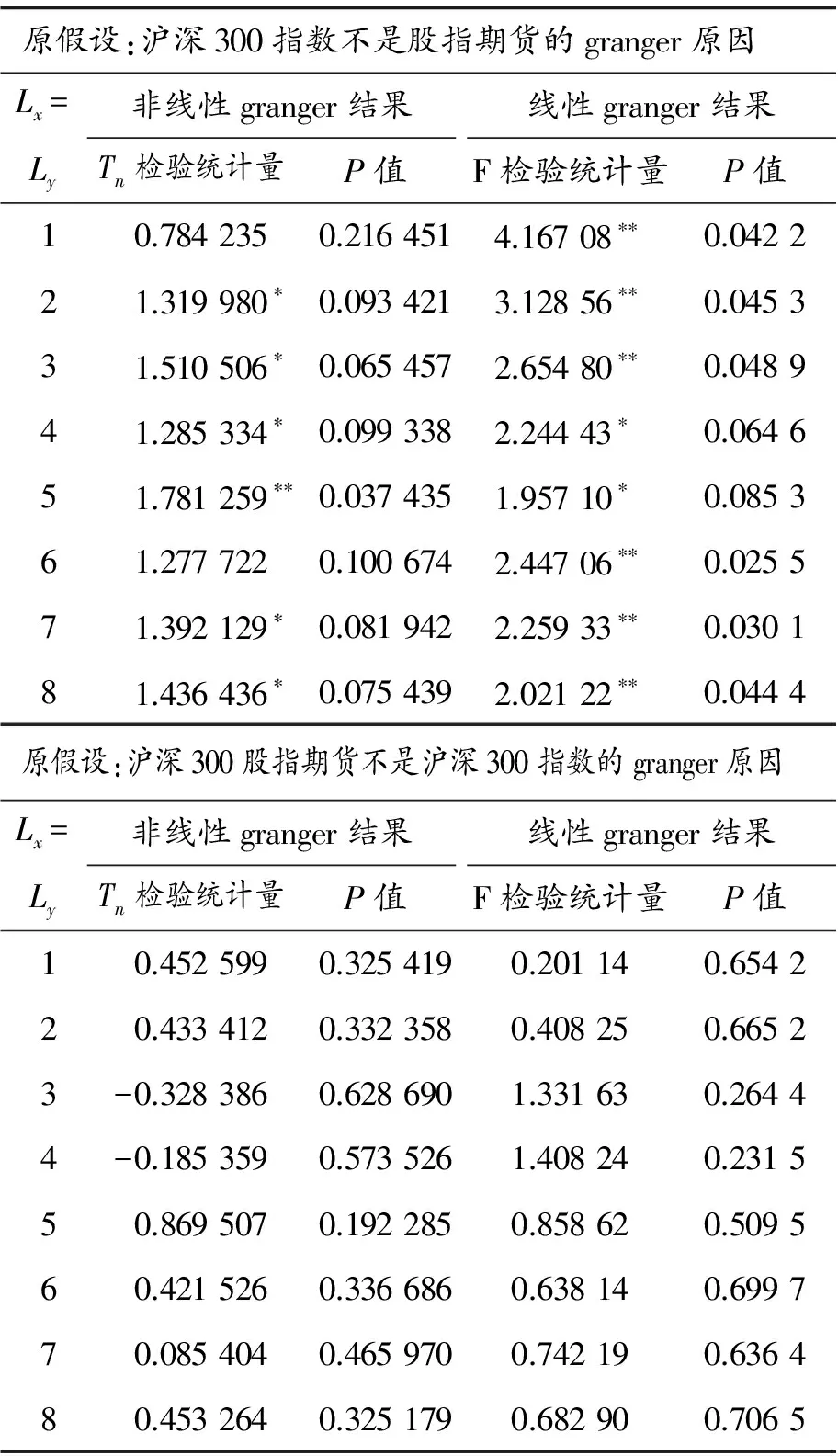
表5 “已实现”波动率序列线性、非线性Granger因果检验结果

注：***、**及*分别表示在1%、5%及10%显著性水平上拒绝“不存在Granger因果关系”的原假设

由以上结果可以看出：在沪深300指数不是沪深300期货的granger原因的假设前提下、滞后期1～8的情况下以及线性granger结果在5%的水平下全部拒绝原假设，非线性granger结果在10%水平下大部分拒绝原假设，这可以更加充分地证明沪深300指数的“已实现”波动率比较显著地引起沪深300股指期货的“已实现”波动率。在沪深300期货是沪深300指数的granger原因的假设前提下，无论是线性granger结果或非线性granger结果均不显著，无法拒绝原假设。说明股指期货的“已实现”波动率对沪深300指数的“已实现”波动率没有明显的影响关系。

3 结束语

本文采用非线性granger因果检验方法——Diks和Panchenko提出的非参数Tn检验方法,并结合传统线性granger因果检验方法，采用5 min价格数据得到我国沪深300指数“已实现”波动率与沪深300股指期货的“已实现”波动率，并对两者波动率之间的线性、非线性关系进行了研究。

经研究发现：沪深300指数与股指期货的“已实现”波动率序列之间均呈现显著的非线性动态变化趋势。同时，线性与非线性granger因果检验结果均表明：沪深300股指期货并不能引起股票市场的震荡，而股票市场的震荡会影响到沪深300股指期货。另外，国内学者基于价格序列之间的波动关系研究结果显示：期现市场的价格序列之间是相互影响的，但本文结果显示：期现市场的波动序列之间的影响是单向的，即仅是股票市场的波动率变化会影响期货市场的波动。

我国沪深300指数期货推出近4年，市场已基本趋近于成熟。本文从线性与非线性两种方法的角度检验期现市场的波动关系，更全面地揭示了两个相关市场高频波动率之间的内在联系，有助于资本市场投资者和政府相关部门了解股指期货推出对现货市场波动风险的影响。另外，沪深300指数与沪深300期货之间的低频波动关系的相互影响关系将是下一步研究和拓展的方向。

[1] ANDERSEN T G,BOLLERSLEV T.Answering the critics:Yes,ARCH models do provide good volatility forecasts[R].USA：National Bureau of Economic Research,1997.

[2] ANDERSEN T,BOLLERSLEV T,DIEBOLD F X,et al.The distribution of realized stock returns volatility[J].Journal of Financial Economics,2001,61:43-76.

[3] GARBADE K D,SILBER W L.Price movements and price discovery in futures and cash markets[J].The Review of Economics and Statistics,1983,65(2):289-297.

[4] SA R.Option and efficiency[J].Quarterly Journal of Economics,1989,90(1):75-89.

[5] ANTONIOS A,PHIL H,RICHARD P.The effects of stock index Future trading on stock index volatility:an analysis of the asymmetric response of volatility to news[J].Journal of Future Market,1998,18:151-166.

[6] ZHONG M,DARRAT A F,OTERO R.Price,discovery and volatility spillovers in index futures markets:some evidence from:mexico[J].Journal of Banking & Finance,2004,28(12):3037-3054.

[7] LI M Y L.The dynamies of the relationship between spot and futures markets under high and low variance regimes[J].Applied Stonehastic Models in Business and Industry,2009,25(6):696-718.

[8] 严敏,巴曙松,吴博.我国股指期货市场的价格发现与波动溢出效应[J].系统工程,2009,27(10):32-38.

[9] 邢精平,周伍阳,季峰.我国股指期货与现货市场信息传递与波动溢出关系研究[J].证券市场导报,2011(2):13-19.

[10] GRANGER C W J.Some recent developments in a concept of causality[J].Journal of Monetary Economics,1988,7:85-106.

[11] 李胜歌,张世英.金融高频数据的最优抽样频率研究[J].管理学报,2008,5(6):801-806.

[12] BROOCK W A,SCHEINKMAN J A,DECHERT W D,et al.A test for independence based on the correlation dimension[J].Econometric reviews,1996,15(3):197-235.

[13] GRANGER C W J.Investigating causal relations by econometric models and cross-spectral methods[J].Econometrica,1969(37):424-438.

[14] 杨子晖,温雪莲.价格国际传递链中的“中国因素”研究——基于非线性Granger因果检验[J].统计研究,2010(2):87-93.

[15] SIMS C A.Macroeconomics and reality[J].Econometirca,1980,48:1-48.

[16] BAEK E,BROCK W.A nonparametric test for independence of a multivariate time series[J].Statistica Sinica,1992(2):137-156.

[17] 周璞,李自然.基于非线性Granger因果检验的中国大陆和世界其他主要股票市场之间的信息溢出[J].系统工程理论与实践,2012(3):466-475.

[18] HIEMSRA C,JONES J D.Testing for linear and nonlinear granger causality in the stock price-volume relation[J].Journal of Finance,1994,54(5):1639-1665.

[19] DIKS C,PANCHENKO V.A new statistic and practical guidelines for nonparametric granger causality testing[J].Journal of Economic Dynamics &Control,2006(30):1647- 1669.

[20] 陈蓉,郑振龙.无偏估计、价格发现与期货市场效率——期货与现货价格关系[J].系统工程理论与实践,2008(8):2-11.

[21] HSIEH D A.Chaos and nonlinear dynamics:application to financial markets[J].Journal of Finance,1991(46):1839-1877.

[22] MOUGOUE M.An empirical re-examination of the dividend-investment relation[J].Quantitative Finance,2008,8(5):533-546.

RelationshipBetweenStockIndexFuturesandSpotMarketinChinaBasedonNon-ParametricTnNonlinearGrangerCausalityTest

GAO Shuang, WANG Lianxin

(College of Management and Economics, Tianjin 300072, China)

The volatility linkages between the CSI 300 stock index and stock index futures is widely concerned by scholars. We firstly use the five minutes high frequency data of CSI 300 stock index and stock index futures to estimate the respective daily realized volatility (RV), while the two variables are highly correlated. Based on the linear and nonlinear Granger causality relationship test, we find that there exists linear and nonlinear Granger causality from the RV of CSI 300 stock index to the RV of stock index futures, but the RV of stock index futures does not cause the RV of CSI 300 stock index.

stock index futures; realized volatility; nonlinear Granger causality relation

2015-02-20

国家自然科学基金资助项目(70901055)

高爽(1987—)，女，硕士，主要从事金融数学研究，E-mail:gaoshuangtju@163.com。

高爽,王联欣.我国股指期货与现货市场的已实现波动关系研究——基于非参数Tn非线性Granger因果关系检验[J].重庆理工大学学报(自然科学)，2017(12):192-198,207.

formatGAO Shuang, WANG Lianxin.Relationship Between Stock Index Futures and Spot Market in China Based on Non-ParametricTnNonlinear Granger Causality Test[J].Journal of Chongqing University of Technology(Natural Science)，2017(12):192-198,207.

10.3969/j.issn.1674-8425(z).2017.12.033

O21

A

1674-8425(2017)12-0192-07

(责任编辑陈 艳)