基于血脑屏障药物渗透机制的建模与分析

王 瑜，尹智勇

(1.山西大学 a.复杂系统研究所； b.数学科学学院；c.疾病防控的数学技术与大数据分析山西省重点实验室， 太原 030006;2.厦门大学 物理系， 福建 厦门 361005)

基于血脑屏障药物渗透机制的建模与分析

王 瑜1a,1b,1c，尹智勇2

(1.山西大学 a.复杂系统研究所； b.数学科学学院；c.疾病防控的数学技术与大数据分析山西省重点实验室， 太原 030006;2.厦门大学 物理系， 福建 厦门 361005)

由于血脑屏障结构的特殊性，脑内疾病的治疗仍然是临床诊疗的一个难点。一般情况下，病人只能通过口服或注射药物来治疗这类疾病。采用理论分析和数值模拟相结合的方法，在控制药物毒性最小的前提下,研究血管和脑组织中游离药物浓度随时间的变化情况。在比较分析未加入超声和加入超声的两个模型后发现：未加入超声时，毛细血管和脑组织中的游离药物浓度在140 min左右达到平衡状态，且平衡点处的药物浓度很低，达不到治疗效果； 而加入超声后，在60～70 s就达到了稳定，同时达到稳态时药物浓度也明显增加。由此可见：加入超声大大减少了服药后大脑组织中药物达到治疗浓度所需的时间，且增加了进入脑组织的药物量。

静脉； 毛细血管； 脂质体； 聚焦超声； 数学模型

血脑屏障(blood-brain barrier,BBB)主要由3部分组成：最内层是脑毛细血管内皮细胞及其之间的紧密连接物，中间是细胞基质和周细胞，最外层是星形胶质细胞及其分泌的细胞外基质[1]，如图1所示。决定BBB特殊性的主要是脑毛细血管内皮细胞，其膜上无孔，细胞间有紧密连接的闭锁小带[2]，导致药物难以通过屏障入脑。研究表明：脂溶性药物且相对分子质量小于400～500才能通过BBB，而几乎所有的大分子药物诸如重组蛋白、基因片段等都不能通过BBB[1]。此外，周细胞是具有免疫功能的细胞，与血管内皮细胞共同构成血管内壁并分泌一些免疫调节物质。外层的星形胶质细胞是组成BBB结构的基础细胞，紧密贴附在BBB内皮组织外表面，与毛细血管互相影响，共同调节BBB的结构和功能[3]。

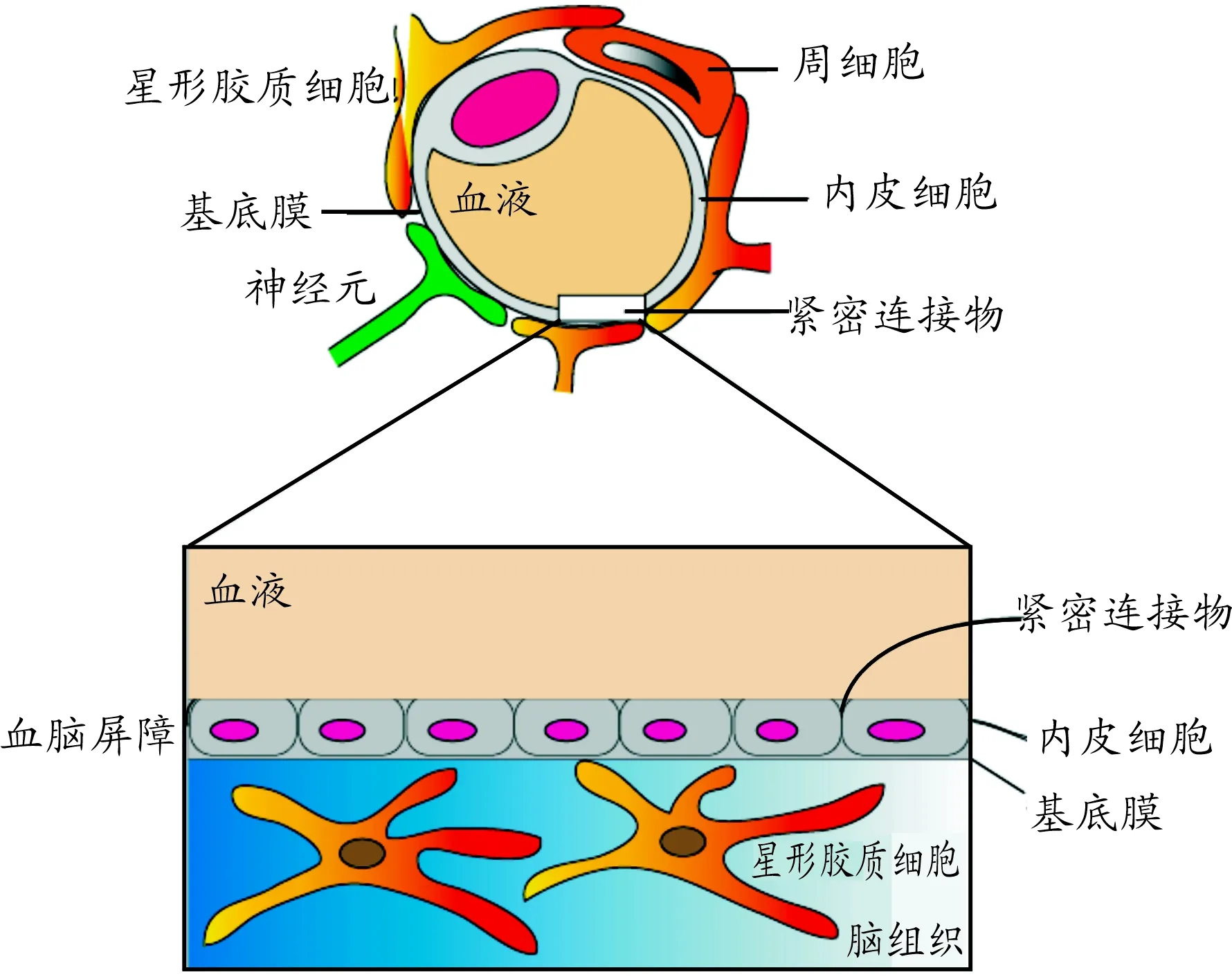
图1 血脑屏障结构示意图

针对BBB结构的复杂性，医学家们研制出载药脂质体，这种脂质体毒副作用小，没有免疫性，可以提高药物的治疗指数和疗效[4]，还可以连接某种特异性的识别分子，通过与靶细胞的特异性识别来实现专一靶向功能。此外，聚焦超声的应用在临床治疗脑内疾病的过程中也成为一个关键，聚焦超声可以重复地引起BBB的破坏且不会明显地引起其他组织的坏死和组织损伤[5]，它的使用不仅大大减少了产生一般生物效应所需要的时间和效果，还能靶向开放BBB，为中枢神经系统疾病的治疗提供一种无创伤的具有靶向性的药物转运方法[6]。

1987年Janzer等[7]研究了星形胶质细胞对BBB的诱导作用。2005年Hawkins等[8]讨论了BBB在人体健康和疾病方面的重要作用。2006年Abbott等[9]研究了星形胶质细胞与内皮细胞相互作用、共同影响和调节BBB的结构和功能。2014年Peter等[10]利用数学模型证实了可以采用低频聚焦超声测量脑内药物浓度，研究了血浆蛋白和游离药物在毛细血管和脑组织之间的相互作用，并呈现了单一药物在BBB中的传递机制，他们利用普通的微分方程描述了毛细血管内血液流动的网络形态，考虑了药物后续的运输和清除。 同一年Peppa[11]指出，数学模型长期被用在医疗卫生组织方面，特别是在与药物运输、传递相关的研究。2017年Anna等[12]利用星形胶质细胞的独特作用去识别脑部神经炎症。

本文基于Peter等的研究，构造了未加入超声和加入超声时药物靶向治疗脑部疾病的两种模型来研究血管和脑组织中游离药物浓度的变化情况，并对未加入超声时的模型进行了定性理论分析，主要讨论了模型正平衡点的存在性和唯一性，并通过Dulac函数证明了正平衡点的全局渐近稳定性。在此基础上引入超声和载药脂质体，再以脂质体靶向大脑给药系统为主体，通过脂质体入脑的机制来建模。该模型解释了一种生物学现象，即在聚焦超声的作用下，BBB能暂时张开，同时脂质体发生破裂释放出游离药物，游离药物通过毛细血管进入脑组织治疗脑内疾病。最后，分别对两种模型进行了数值模拟，并比较了两种模型下游离药物浓度的变化情况以及加入超声后的模型中脂质体的浓度变化情况。

1 模型的建立与分析

1.1 模型的建立

基于2014年Peter 等[10]的工作，为了数学上的分析方便，降低了模型的复杂度，仅考虑大脑中某一个毛细血管内药物传输到大脑的动力学过程，忽略周边其余毛细血管可能存在的影响。为了使系统便于分析和计算，进一步做出如下假设：脂质体的半衰期与血浆的半衰期同步发生；患者只在口服或注射的条件下摄入药物；大脑组织中游离药物会产生新陈代谢。先考虑不加入超声时的系统，系统流程如图2所示。

图2 未加超声的系统流程

图2中：v表示毛细血管中游离药物的浓度；w表示脑组织中游离药物的浓度。将图2所示的毛细血管中游离药物和脑组织中游离药物相互作用的流程转换成微分方程组后得到以下模型：

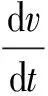
(1)

模型中参数解释和取值见表1。由表1可知K>1，V>1。

在模型(1)的基础上进一步考虑加入超声并引入脂质体模型，为了确保注入的脂质体可以充分地在超声作用下发生破坏并释放出游离药物，做出如下假设：在加入超声1 min后周期性地注射脂质体，且脂质体在超声作用下并没有完全发生破裂。因此，在分析脂质体破裂和超声强度的关系时考虑饱和发生率，根据这一机理得到如下模型：

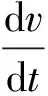
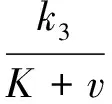
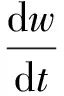
(2)

其中：u表示毛细血管中脂质体的浓度；a、b为饱和发生率系数。

1.2 模型分析

1.2.1 符号说明与研究方法介绍

由于药物只有进入脑组织后才能对疾病产生治疗的效果，因此本文主要以w作为指标变量分析其动力学过程。首先证明了模型(1)存在唯一的正平衡点，然后通过构造Dulac函数分析正平衡点的全局稳定性。数值模拟主要是在Matlab软件下执行。Matlab软件主要是模拟游离药物浓度v、w的时间序列变化以及v、w之间的关系。本文所涉及的参数如表1所述。

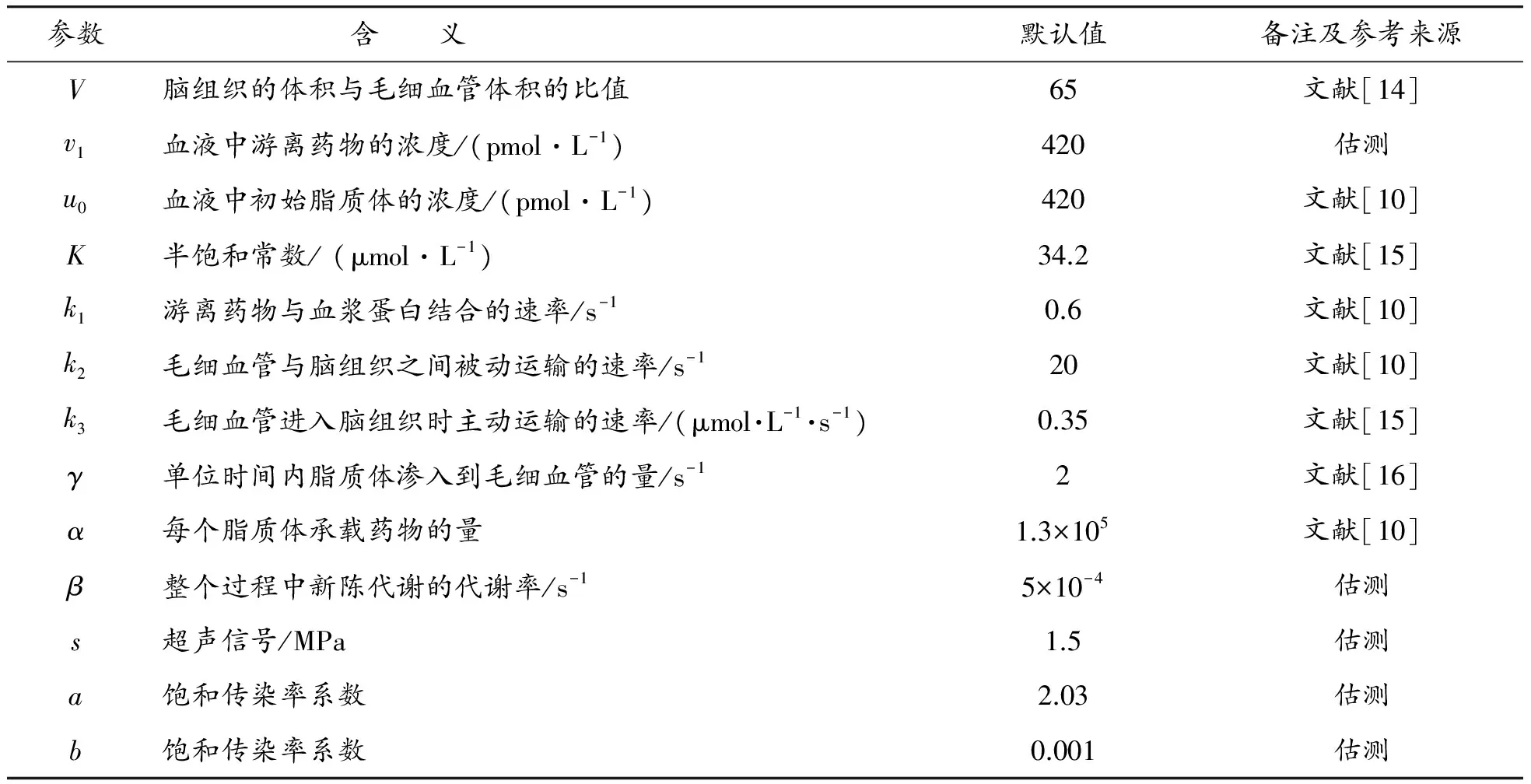
表1 模型中所涉及的参数标准值列表

注：半饱和常数K指的是主动运输速率达到最大速率的一半时毛细血管中游离药物的浓度。

1.2.2 理论分析

以下针对本文所述的机理进行分析，包括定性理论分析和数值模拟。定性分析主要是正解的存在性和唯一性分析以及正平衡点全局稳定性的证明，数值模拟主要是对游离药物浓度时间序列的模拟。由于模型中的参数都是具有生物学意义的，为了确保研究合乎情理，本文各模型中参数都为正值，根据这一条件，我们做出以下分析。

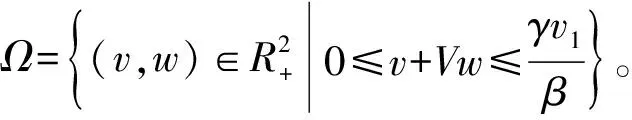
证明若∃T0>0, s.t.首次出现T0时T0=inf{t≥0,v(t)=0 或w(t)=0}，对t∈[0,T0)，v(t)>0,w(t)>0，不失一般性，设对于所有的t∈[0,T0],v(T0)=0,w(t)≥0，则有：v′(t)|t = T0=γv1+k2w(T0) > 0，因此v(t)不会变成负的。

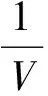
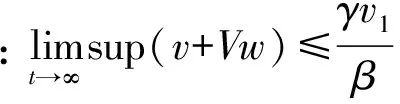
定理2 系统(1)存在唯一的正平衡点。

证明令系统(1)的右端等于0，则有：

(3)

方程组(3)两式相加可得：

(4)

将w的表达式代入方程组(3)整理可得：av2+bv+c=0，其中：

a=(k1+k2+γ)βV+k1k2+k2γ>0

b=(Kk2+k3+Kk1+Kγ-γv1)βV+

Kk1k2-k2γv1+Kk2γ

c=-(Kk2γv1+Kγv1βV)<0

(5)

定理3 系统(1)的正平衡点是全局渐近稳定的。

证明 系统(1)在正平衡点E(v*,w*)处的雅可比矩阵为：

(6)

因此， 雅可比矩阵(6)的特征方程为λ2+mλ+n=0，其中：

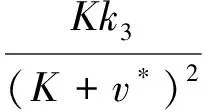
利用Hurwitz判据[17]判断：

(7)

故系统(1)的雅可比矩阵的所有特征值都具有负实部，系统(1)的正平衡点局部渐近稳定。

以下用Dulac函数来判断系统(1)的全局稳定性。

记：

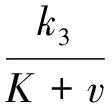
(8)

取H(v,w)=v-1w-1，则有：

H(v,w)P(v,w)=γv1v-1w-1-

(9)

从而有：

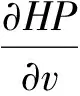
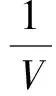
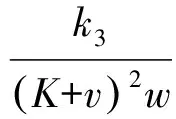
(10)

综上，根据Δ<0和Dulac函数理论[17]可知系统(1)不存在极限环，又因系统是局部稳定的，故整个系统全局渐近稳定。

注意到本研究是利用Dulac函数的一般性来分析模型的动力学行为，这里主要分析游离药物到达脑组织后呈现的稳定状态。到目前为止，所有的理论分析都集中在数学模型和其动力学行为上，例如正平衡点的存在性、唯一性和全局渐近稳定性。接下来通过对加入超声和未加入超声时药物靶向治疗脑部疾病的两种模型进行数值模拟，以此具体、直观地描绘药物靶向治疗脑部疾病的过程中游离药物浓度随时间的变化。

2 数值模拟

在药物从毛细血管通过血脑屏障进入脑组织这一动力学过程中，血脑屏障的完好与否以及药物通过血脑屏障的量直接决定了疾病的治疗效果。为了验证前面的相关分析所得到的理论性结果以及两种模型的准确性，以下利用表1中的参数值进行数值模拟。

首先，依据模型(1)中求解出的正平衡点的值，分别取正平衡点附近的值作为游离药物浓度的初值进行模拟。选择v、w的初值分别为v=w=0.000 318，v=w=0.000 32，在这两组参数下，模拟了游离药物浓度v、w随时间变化的时间序列(如图3所示)。其中：b、d分别表示w初值取0.000 32和0.000 318时游离药物浓度随时间的变化；a、c分别表示v的初值取0.000 32和 0.000 318时游离药物浓度随时间的变化； 游离药物v、w的浓度都达到了全局渐近稳定。

图4模拟了游离药物浓度v、w的相图，即v、w在变化过程中产生的向量场中的矢量线逐渐趋于全局渐近稳定的关系。其中黑色虚线、蓝色实线分别表示脑组织和毛细血管中游离药物浓度w、v的零斜率线，其交点即为系统的正平衡点，向量场中的矢量线都将先向v的零斜率线逼近，然后顺着零斜率线逼近系统的正平衡点。

图5在固定时滞τ=1的前提下，选取：a=2.03，b=0.001，s=0.85；a=2.03，b=0.001，s=1.45；a=2.03，b=0.001，s=1.5；a=2.03，b=0.001，s=1.6。在这4组参数下以s为指标变量模拟了加入超声后超声对游离药物进入脑组织的量的影响。从图5(a)可以看出：脂质体在周期性的注射过程中，经历了从刚开始的阻尼振荡到振荡再到最后反向阻尼振荡的过程。从图5(b)可以看出：毛细血管中的游离药物浓度在62 s左右开始达到稳定的状态，而脑组织中的游离药物浓度在72 s左右开始达到稳定的状态。整个过程中，在饱和率系数不变的情况下，随着超声强度的增大，饱和率系数也在不断地增大，系统会保持一定时间的稳定性，保证u、v的正性，出现阻尼振荡。当超声强度达到人体能够承受的最大超声强度时，u、v的浓度达到最大，系统产生周期性的振荡。再加大超声强度时，超出人体能够承受的范围，u、v的正性和周期系统的稳定性被破坏，不再呈现原有的状态，出现反向阻尼振荡的现象。与前面所述未加入超声时得到的结果相比，加入超声可以增加游离药物进入脑组织的量，使得疗效更佳，也说明引入超声对脑部疾病进行治疗具有很重要的作用。

就生物学意义而言，未加入超声时，游离药物浓度v、w在正平衡点E(v*,w*)处达到了全局稳定，这也描述了一种生物扩散现象，即大部分游离药物在毛细血管中会与血浆蛋白结合而留在血管内，少部分的药物会扩散到脑组织，当脑组织内外浓度达到平衡态时不再发生扩散现象。而加入超声可以降低血管中游离药物与血浆蛋白的结合速率，同时加快游离药物通过血脑屏障进入脑组织的速率，增加药物进入脑组织的量，对疾病产生更为理想的治疗效果。

图3 系统(1)中游离药物v、w的时间序列

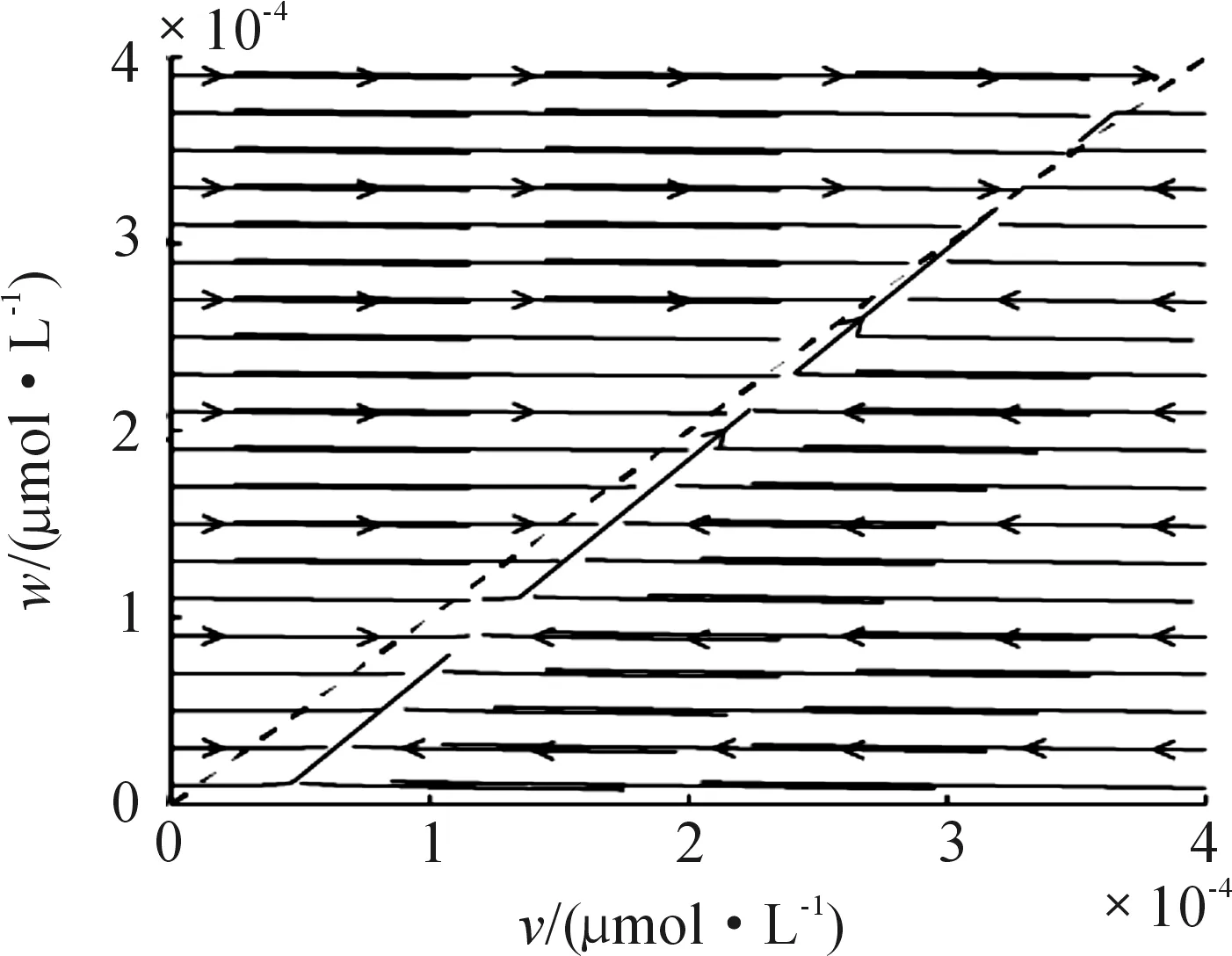
图4 系统(1)中游离药物v、w的关系

3 结束语

本文通过构造Dulac函数，对游离药物进入脑组织靶向治疗脑部疾病的动力学模型进行了理论分析，主要包括正平衡点的存在性、唯一性分析和全局渐近稳定性的证明以及相应的数值模拟，最终得出结论：正平衡点存在且唯一，并且该模型的正平衡点是全局渐近稳定的。

在上述模型的基础上引入超声和脂质体，用数学模型描述药物在静脉血管、毛细血管以及脑组织中的传递与吸收效果，从模拟结果(图5)可以看出，加入超声大大增加了药物进入脑组织的量，且脂质体和游离药物的浓度最终也达到了稳定状态。

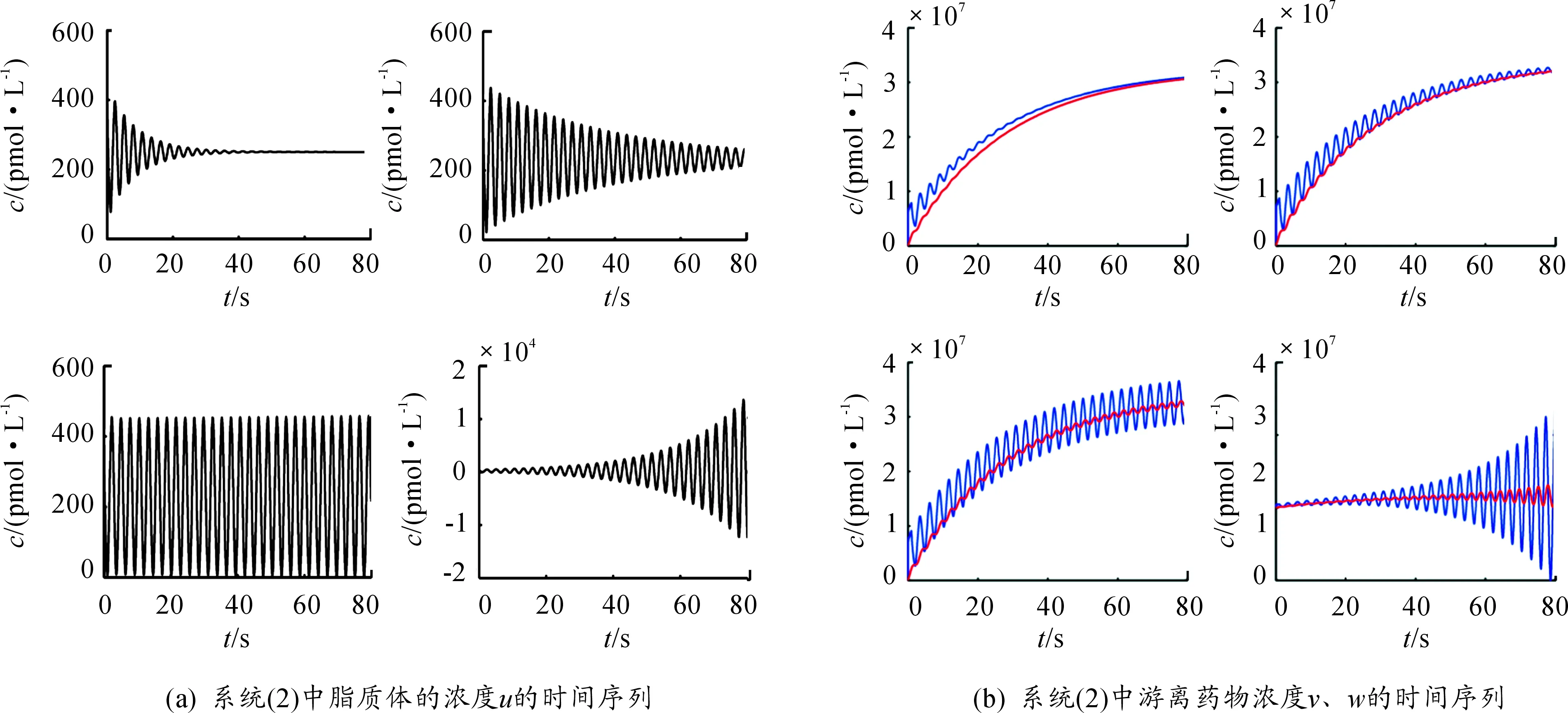
图5 模拟结果

对比以上两种模型，其数值模拟结果都给出了较为合理的解释和推测。针对未加入超声的模型所得结果展开了讨论和分析。模型(1)的结果反映出全局渐近稳定性，模型(2)的结果反映出游离药物在脑组织中浓度达到最大值的时间以及游离药物最大量与注入脂质体浓度的关系。通过模拟得到：加入超声大大减少了服药后大脑组织中药物达到治疗浓度所需的时间，且增加了药物进入脑组织的量，可以对治疗提供参考依据。

本文的建模也存在一些不足：针对模型(1)的建模仅局限于大脑中某一个毛细血管内药物传输到大脑的动力学过程，忽略周边其余毛细血管可能存在的影响。之后可以接着讨论脑部所有毛细血管(一个整体)与脑组织之间的相互作用以及对加入超声后的模型进行一定的理论分析和后续的模拟，也可以分析加入超声后时滞变化对模拟结果的影响。我们期待将来的研究对脑部给药系统有更深刻的阐述和认识，为这些人类相关疾病如脑瘤的调控和治疗提供思路和参考。

[1] BICKER J,ALVES G,FORTUNA A,et al.Blood-brain barrier models and their relevance for a successful development of CNS drug delivery systems:a review[J].European Journal of Pharmaceutics and Biopharmaceutics,2014,87(3):409-432.

[2] 张哲明，陈丽青.脑靶向纳米给药系统研究进展[J].国际药学研究杂志，2016，43(5)：887-892.

[3] 吴华夏.脑靶向给药方式及研究进展[J].上海医药，2010，31(1)：35-37.

[4] 陈吉祥，李广林.脂质体在生物学中的应用新进展[J].中国农业科学院兰州畜牧与兽医研究所，2000，30(3)：28-29.

[5] ARYAL M,ARYANITIS C D,ALEXANDER P M,et al.Ultrasound-mediated blood-brain barrier disruption for targeted drug delivery in the central nervous system[J].Advanced Drug Delivery Reviews,2014,72:94-109.

[6] 李光华.药物通过血脑屏障向脑内分布的方法研究[J].天津药学，2013，24(6)：66-68.

[7] JANZER R C,RAFF M C.Astrocytes induce blood-brain barrier properties in endothelial cells[J].Nature,1987,325(6101):253-257.

[8] HAWKINS B T,DAVIS T P.The blood-brain barrier/neurovascular unit in health and disease[J].Pharmacological Reviews,2005,57(2):173-185.

[9] ABBOTT N J,RONNBACK L,HANSSON E.Astrocyte-endothelial interactions at the blood-brain barrier[J].Nature Reviews Neuroscience,2006,7(1):41-53.

[10] HINOW P,RADUNSKAYA A,MACKAY S M,et al.Signaled drug delivery and transport across the blood-brain barrier[J].Journal of Liposome Research,2016,26(3):233-245.

[11] BRASNJEVIC I,STEINBUSCH H W M,SCHMITZ C,et al.Delivery of peptide and protein drugs over the blood-brain barrier[J].Progress in Neurobiology,2009,87(4):212-251.

[12] HERLAND A,VANDERMEER A D,FitzGerald E A,et al.Distinct contributions of astrocytes and pericytes to neuro inflammation identified in a 3D human blood-brain barrier on a chip[J].PLOS One,2016,11(3):e0150360.

[13] KLEINFELD D,MITRA P P,HELMCHEN F,et al.Fluctuations and stimulus-induced changes in blood flow observed in individual capillaries in layers 2 through 4 of rat neocortex[J].Proceedings of the National Academy of Sciences,1998,95(26):15741-15746.

[14] BAR T.The vascular system of the cerebral cortex[M].USA：Springer Science & Business Media,2012.

[15] DELAMO E M,URTTI A,YLIPERTTULA M.Pharmacokinetic role of L-type amino acid transporters LAT1 and LAT2[J].European Journal of Pharmaceutical Sciences,2008,35(3):161-174.

[16] CUMMING P,GJEDDE A.Compartmental analysis of dopa decarboxylation in living brain from dynamic positron emission tomograms[J].Synapse,1998,29(1):37-61.

[17] 马知恩，周义仓.常微分方程定性与稳定性方法[M].北京：科学出版社，2012.

ModelingandAnalysisofDrugPermeationMechanismBasedonBlood-BrainBarrier

WANG Yu1a, 1b, 1c，YIN Zhiyong2

(1.a.Complex System Research Center; b.School of Mathematical Sciences; c.Shanxi Key Laboratory of Mathematical Techniques and Big Data Analysis on Disease Control and Prevention, Shanxi University, Taiyuan 030006, China; 2.Department of Physics, Xiamen University, Xiamen 361005, China)

Treatment for the intracerebral diseases has been a challenging issue in clinical diagnosis and treatment. Because of the special brain barrier structure, patients generally treat these diseases only through oral or injection drugs. In order to make it clear, this paper theoretically and numerically studies the variation laws of free drug concentration in the vascular and brain tissue given minimizing the toxicity of drugs. After comparing two models without and with ultrasound treatments, we find that at the absence of ultrasound treatment it takes about 140 minutes that the concentration of free drugs in capillary and brain tissue reaches the balance state. In this case, drug concentration is greatly low, which does not achieve an ideal therapeutic effect. Otherwise, it only takes approximately 60 to 70 minutes to reach the balance state with ultrasound treatments and drug concentration significantly increases. That greatly reduces the time taken for drugs to reach therapeutic concentration in brain tissue and increases the amount of drugs entering the brain tissue.

vein; capillary; liposome; focused ultrasound; mathematical model

2017-09-20

疾病防控的数学技术与大数据分析山西省重点实验室资助项目(201705D111006)； 山西省动物群发病科技数据服务共享平台项目(201605D121014)

王瑜(1992—),女,硕士研究生,主要从事传染病传播动力学研究,E-mail:18834810643@163.com； 尹智勇(1992—),男,博士研究生,主要从事癌细胞的信号网络动力学研究,E-mail:yinzhiyong1992@163.com。

王 瑜，尹智勇.基于血脑屏障药物渗透机制的建模与分析[J].重庆理工大学学报(自然科学)，2017(12):122-129.

formatWANG Yu，YIN Zhiyong.Modeling and Analysis of Drug Permeation Mechanism Based on Blood-Brain Barrier[J].Journal of Chongqing University of Technology(Natural Science)，2017(12):122-129.

10.3969/j.issn.1674-8425(z).2017.12.021

O175

A

1674-8425(2017)12-0122-08

(责任编辑何杰玲)