一类微生物流加发酵过程的动态优化

王 丹，李彩霞，徐恭贤

(渤海大学 数理学院， 辽宁 锦州 121013)

一类微生物流加发酵过程的动态优化

王 丹，李彩霞，徐恭贤

(渤海大学 数理学院， 辽宁 锦州 121013)

研究了甘油生物歧化为1，3-丙二醇的流加发酵过程。针对甘油生物歧化为1，3-丙二醇过程的流加发酵系统，建立了在终端时刻是固定值的前提下，以1，3-丙二醇的浓度达到最大值为目标函数的动态优化模型。采用有限元配置法，将甘油流加生物歧化为1，3-丙二醇过程的状态方程转换为代数方程，进而得到模型的NLP(非线性规划)形式。运用Matlab软件求解所建立的动态优化模型，并针对所得到的优化结果进行分析及讨论。

1，3-丙二醇；动态优化；流加发酵；有限元配置法

1，3-丙二醇是一种非常重要的化工原料，如溶剂、抗冻剂或保护剂、精细化工原料以及聚合物单体等[1-2]。与传统的化学合成法相比，微生物法具有转化率高、副产物少、环境污染小等优点[3]，但要提高1，3-丙二醇的浓度依然是很难解决的问题。因此，甘油生物歧化生产1，3-丙二醇日益受到关注。

近年来，越来越多的学者们热衷于对甘油歧化微生物生产1，3-丙二醇过程的研究。杨杰通过建立单目标和多目标动态优化模型，研究了微生物间歇发酵生产1，3-丙二醇过程的优化问题[4]。徐恭贤等对发酵过程提出新的迭代优化策略，并且进行优化控制的研究[5]。孙亚琴等[6]建立了甘油生物歧化为1，3-丙二醇过程还原途径酶催化8维非线性动力系统。宫召华等[7]建立了最优控制模型，利用不可微优化理论得到了最优控制问题的最优性条件，并证明了最优性条件和最优性函数零点的等价性。谭雯心[8]建立了以各代谢物的浓度误差与斜率误差之和为目标函数的参数辨识动态优化模型。文献[9-12]等基于代谢工程方法对主要产物1，3-丙二醇的生产改善问题进行了研究。高群王等[13]提出了一个使主要产物1，3-丙二醇产率达到最大的稳态优化模型。文献[14-16]研究了甘油连续生物歧化为1，3-丙二醇过程的多目标优化问题。徐恭贤等[17]研究了甘油间歇生物歧化过程的动态优化，获得更高的1，3-丙二醇产率。

本文针对微生物流加发酵生产1，3-丙二醇过程的动态优化问题，建立与其过程特点相适应的动态优化模型，并提出有效的算法求解该模型，结果表明方法有效。

1 流加发酵过程的数学模型

微生物流加过程的方程式描述如下：

(1)

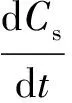
(2)

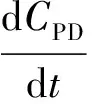
(3)

(4)

(5)

(6)

(7)

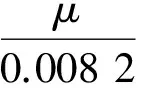
(8)

(9)

(10)

(11)

t∈[0,tf]

(12)

其中：Cx是生物量(g·L-1)；μ和μm分别是比生长速率及其最大值(h-1)；Cs是底物浓度(mmol·L-1)；CPD，CHAc，CEtOH是产物浓度(mmol·L-1)；t是发酵时间(h)；qs是底物比消耗速率(mmol·g-1·h-1)；qPD，qHAc，qEtOH是产物比生成速率(mmol·g-1·h-1)；F是甘油流加速率 (L·h-1)；V是反应器中液体体积(L)；r是碱的流加速率与甘油流加速率的比。

2 优化模型

以终端时刻是固定值为前提，1，3-丙二醇的浓度达到最大为目标函数，建立如下动态优化模型：

maxf=CPD(tf)

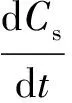
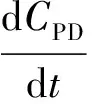
(13)

0≤t≤tf

0≤Cx≤5

0≤Cs≤2 039

0≤CPD≤939.5

0≤CHAc≤1 026

0≤CEtOH≤360.9

5≤V≤8

0≤F≤0.9

3 有限元配置法

为了方便叙述，设x=(x1,x2,x3,x4,x5,x6)T=(Cx,Cs,CPD,CHAc,CEtOH,V)T

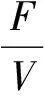
f6(x)=F+rF

G(x(tf),tf)=CPD(tf)

u(t)=F

则可将问题(13)表示为下列优化问题：

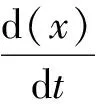
x≤(5,2039,939.5,1026,360.9,VU)T

x≥(0,0,0,0,0,VL)T

(14)

u(t)L≤u(t)≤u(t)U

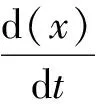
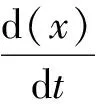
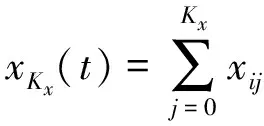
(15)

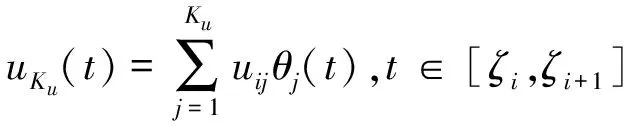
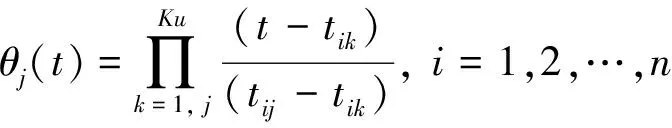
(16)

其中：Kx为有限元[ζi,ζi+1]上配置点的个数。拉格朗日多项式xKx(t)满足xKx(tij)=xij，uKu(t)满足uKu(tij)=uij。为了确定拉格朗日多项式xKx(t),uKu(t)的系数，将其代入状态方程中，则可得配置方程：

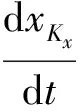
k=1,2,…,Kx

(17)

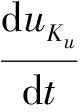
k=1,2,…,Ku

(18)

令tik=ζi+Δζiτk, Δζi=ζi+1-ζi,τk∈[0,1]，则可将式(17)、(18)写为：

k=1,2,…,Kx

(19)

k=1,2,…,Ku

(20)

另外，为了确保状态在有限元终端处具有连续性，相邻有限元的初始状态和终端状态需满足以下条件：

基于上述分析可将动态优化问题(14)转化为如下NLP问题：

i=1,2,…,n,j=0,1,…,Kx

i=1,2,…,n,j=0,1,…,Ku

(21)

i=1,2,…,n,j=1,2,…,Ku

xKx(tij)≤(5,2039,939.5,1026,360.9,VU)T,

xKx(tij)≥(0,0,0,0,0,VL)T

i=1,2,…,n,j=1,2,…,Kx

4 优化结果与分析

本文在Matlab上用其优化工具箱求解NLP问题(21)。表1 给出不同的终端时刻下，动态优化问题的最优解。如表1所示，随终端时刻tf逐渐增大，Cx(tf)逐渐减小，最小值为1.79 mmol·L-1；Cs(tf)先逐渐增大，然后减小，在31 h升到最大1 186.68 mmol·L-1；CPD(tf)始终可达到最大值939.5 mmol·L-1；CHAc(tf)的值先减小，在终端时刻为25 h时，增大至230.63 mmol·L-1，然后逐渐降低；CEtOH(tf)、V(tf)和F的值都是先增大，在20 h到28 h内逐渐减小，然后增大，CEtOH(tf)最大可达到139.99 mmol·L-1，V(tf)在终端时刻为28 h时达到最大值7.57 mmol·L-1，F最大可达到0.41 mmol·L-1。

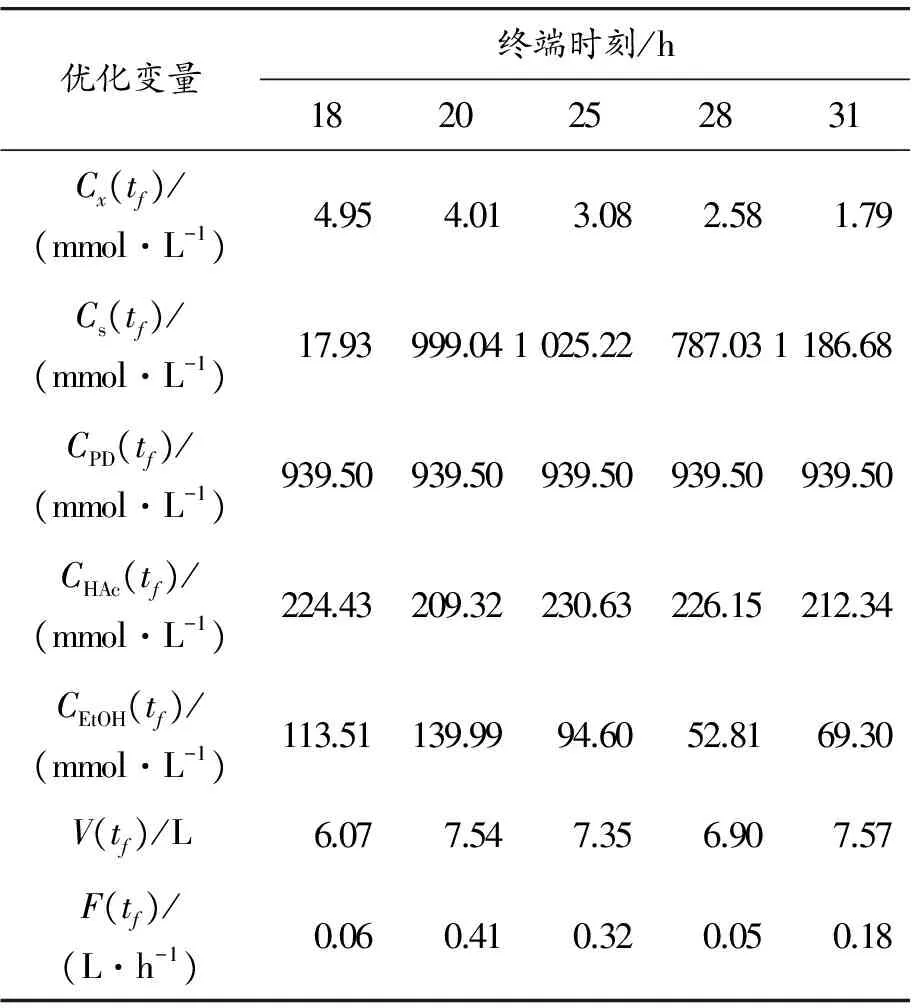
表1 不同终端时刻动态优化问题的最优解

图1～7为终端时刻取20 h时，底物和产物随发酵时间t的变化曲线。

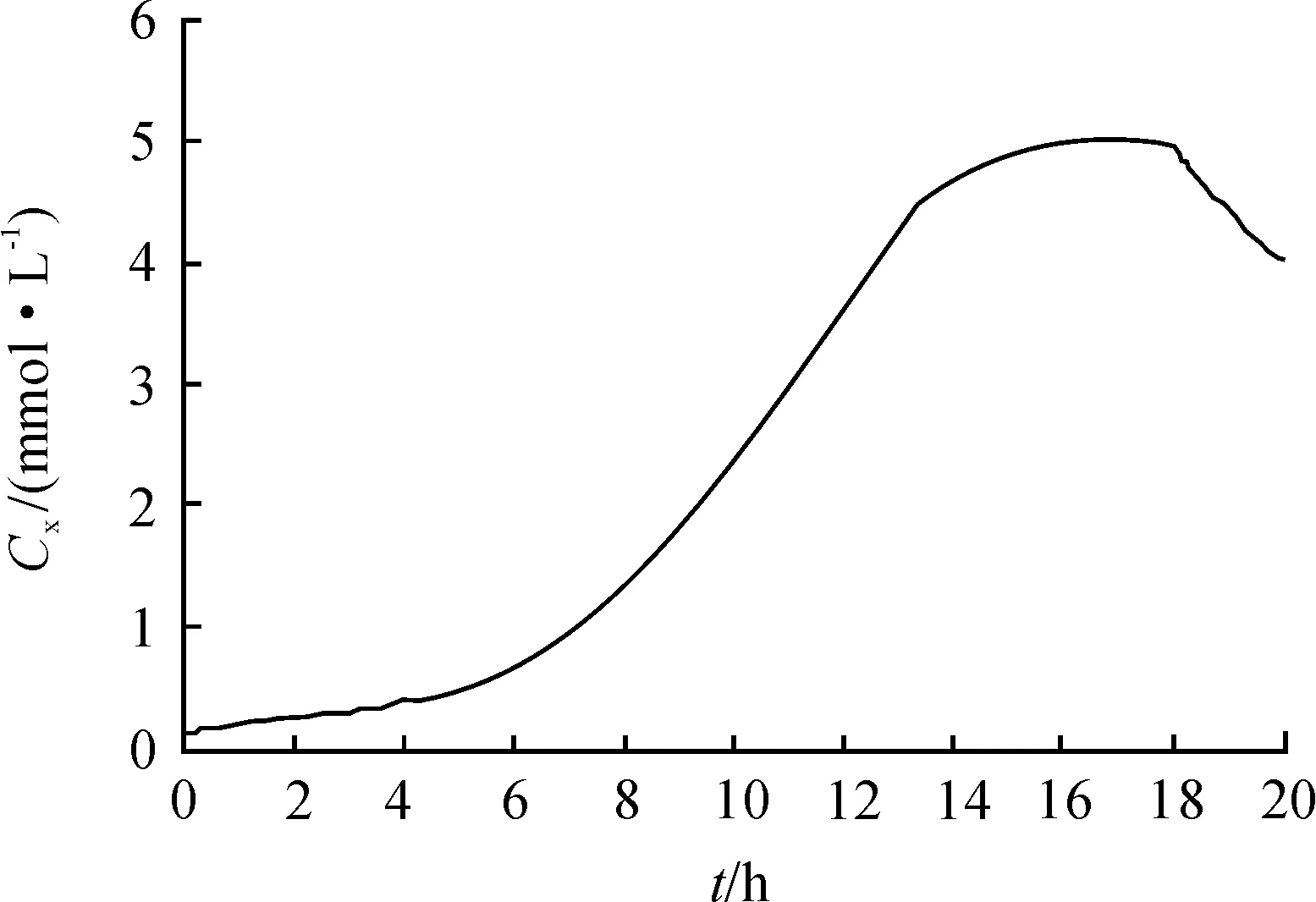
图1 生物量的变化曲线

图2 甘油浓度的变化曲线

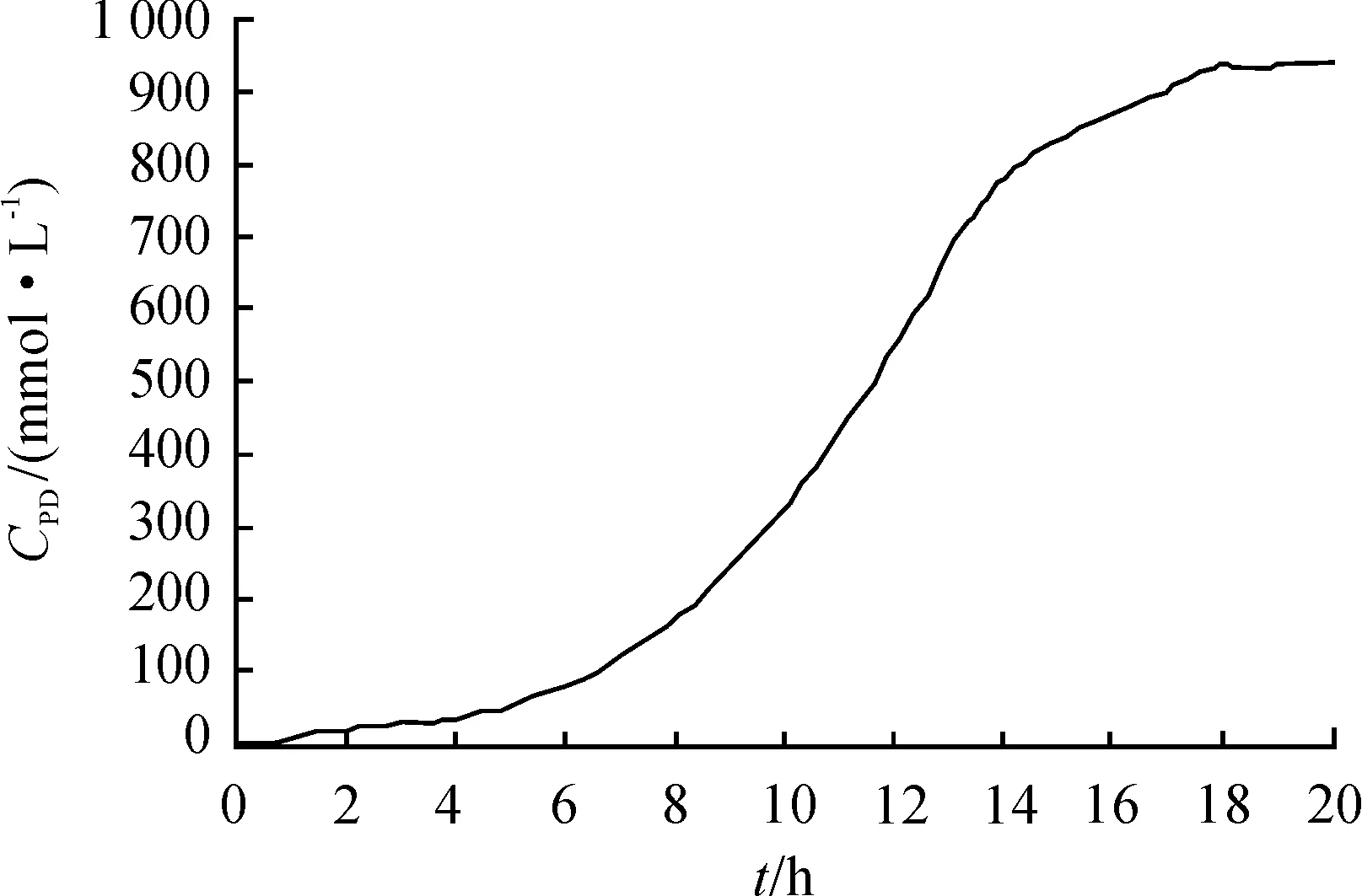
图3 1，3-丙二醇浓度的变化曲线

图4 乙酸浓度的变化曲线

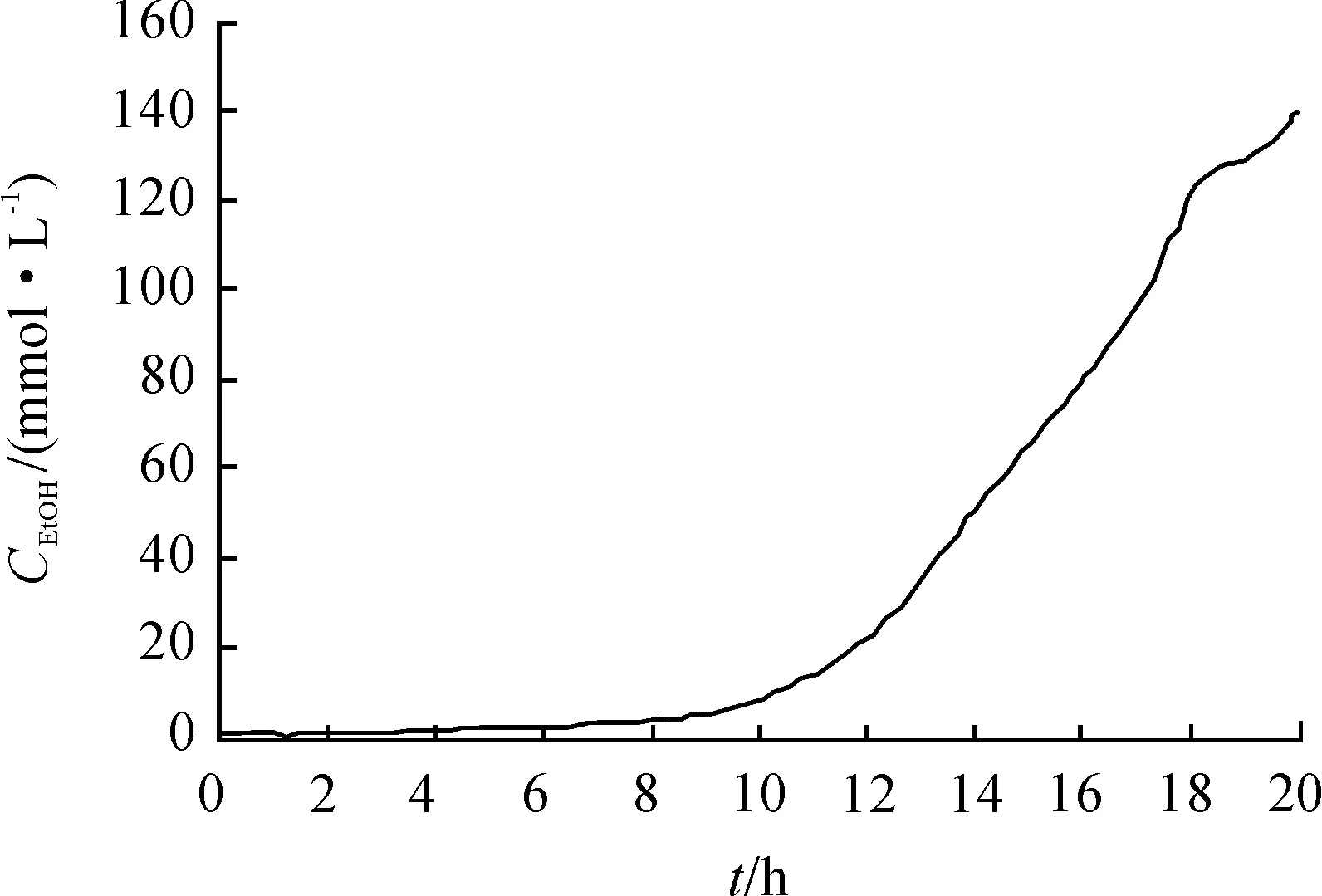
图5 乙醇浓度的变化曲线

图6 反应器中液体体积的变化曲线

图7 甘油流加速率的变化曲线

5 结束语

本文针对甘油流加生物歧化生产1，3-丙二醇的过程，研究了其动态优化问题。以终端时刻产物1，3-丙二醇的浓度作为目标函数，提出了动态优化模型，并利用有限元配置法结合Matlab软件求解了所提出的优化问题。本文通过取不同的终端时刻值，获得底物消耗和产物生成的变化情况，为实现甘油流加生物歧化过程的工业生产优化提供了指导。计算结果表明：终端时刻1，3-丙二醇的浓度可达到其最大允许值。

[1] 孙亚琴.甘油生物歧化过程酶催化和基因调控的非线性数学模拟与分析[D].大连:大连理工大学，2010.

[2] 修志龙.1,3-丙二醇的微生物法生产分析[J].现代化工，1999，19(3):33-35.

[3] 徐恭贤，邵诚，钱伟懿.非线性生化过程的优化与控制[M].北京:科学出版社，2015.

[4] 杨杰.一类微生物发酵过程的动态优化[D].锦州:渤海大学，2015.

[5] XU G X，SHAO C，XIU Z L.Optimizing control of bio-dissimilation process of glycerol to 1，3-propanediol[J].Chinese Journal of Chemical Engineering，2008，16(1):128-134.

[6] SUN Y Q，QI W T，TENG H，et al.Mathematical modeling of glycerol fermentation by Klebsiella pneumoniae:Concerning enzyme-catalytic reductive pathway and transport of glycerol and 1，3-propanediol across cell membrane[J].Biochemical Engineering Journal，2008，38:22-32.

[7] 宫召华，冯恩民.微生物批式流加发酵多阶段最优控制的最优性条件[J].运筹学学报，2009，13(4):109-119.

[8] 徐恭贤，谭雯心，王佳星.一类微生物间歇发酵过程的参数辨识[J].重庆理工大学学报(自然科学)，2016(10):76-80.

[9] KUMAR V，DURGAPAL M，SANKARANARAYANAN M，et al.Effects of mutation of 2，3-butanediol formation pathway on glycerol metabolism and 1，3-propanediol production by Klebsiella pneumoniae J2B[J].Bioresource Technology，2016，214:432-440.

[10] CHEN Z,LIU H J，LIU D H.Metabolic pathway analysis of 1，3-propanediol production with a genetically modified Klebsiella pneumoniae by overexpressing an endogenous ADPH-dependent alcohol dehydrogenase[J].Biochemical Engineering Journal，2011，54(3):151-157.

[11] WISCHRAL D，ZHANG J，CHENG C，et al.Production of 1，3-propanediol by Clostridium beijerinckii DSM 791 from crude glycerol and corn steep liquor： Process optimization and metabolic engineering[J].Bioresource Technology，2016，212:100-110.

[12] HIROKAWA Y，MAKI Y，TATSUKE T，et al.Cyanobacterial production of 1，3-propanediol directly from carbon dioxide using a synthetic metabolic pathway[J].Metabolic Engineering，2016，34:97-103.

[13] 高群王，徐恭贤，王佳星.一类生物过程的稳态优化[J].重庆理工大学学报(自然科学)，2015(10):152-158.

[14] ZENG A P，XIU Z L，AN L J.Mathematical modeling of kinetics and research on multiplicity of glycerol bioconversion to 1，3-propanediol[J].Journal of Dalian University of Technology，2000，40(4):428-433.

[15] TAG C G.Mikrobielle herstellung von 1，3-propanediol[D].Oldenburg:University of Oldenburg，1990.

[16] 高群王，李杨，宋一凡，等.一类连续生物过程的双目标优化[J].渤海大学学报(自然科学版)，2016,37(3):152-158.

[17] 徐恭贤，杨杰.甘油间歇生物歧化过程的动态优化[J].计算机工程与应用，2017，53(10):258-263.

[18] BIEGLER L T.Nonlinear programming:Concepts，algorithm，and applications to chemical processes[M].Philadelphia:SIAM，2010.

DynamicOptimizationforaClassofMicrobialFed-BatchFermentationProcess

WANG Dan， LI Caixia， XU Gongxian

(College of Mathematics and Physics, Bohai University, Jinzhou 121013, China)

The fed-batch fermentation process of glycerol bio-dissimilation to 1, 3-propanediol was studied. A dynamic optimization model with the maximum concentration of 1, 3-propanediol as the objective function was established under the premise that the terminal time was a fixed value for the fed-batch fermentation system with glycerol bio-dissimilation as 1, 3-propanediol. The NLP (nonlinear programming) form of the model was obtained by using collocation on finite elements method to convert the state equation of the glycerol bio-dissimilation to the 1, 3-propanediol process to the algebraic equation. The dynamic optimization model was solved by Matllab software, and the optimization results were analyzed and discussed.

1, 3-propanediol; dynamic optimization; fed-batch fermentation; collocation on finite elements method

2017-06-10

国家自然科学基金资助项目(11101051，11371071)；辽宁省自然科学基金资助项目(2015020038)

王丹(1993—),女,黑龙江五大连池人,硕士研究生,主要从事最优化方法与应用研究，E-mail:844364936@qq.com；通讯作者 徐恭贤(1976—)，男，辽宁庄河人,博士,副教授,主要从事最优化方法与应用方面的研究，E-mail:gxxu@bhu.edu.cn。

王丹，李彩霞，徐恭贤.一类微生物流加发酵过程的动态优化[J].重庆理工大学学报(自然科学)，2017(12):116-121.

formatWANG Dan， LI Caixia， XU Gongxian.Dynamic Optimization for a Class of Microbial Fed-Batch Fermentation Process[J].Journal of Chongqing University of Technology(Natural Science)，2017(12):116-121.

10.3969/j.issn.1674-8425(z).2017.12.020

O29

A

1674-8425(2017)12-0116-06

(责任编辑何杰玲)