HSK与BT工具系统动平衡性能比较分析

陈世平，曾凡宇，王振振,李青锋

(1.重庆理工大学 机械工程学院， 重庆 400054;2.重庆铁马专用车有限公司， 重庆 402246)

HSK与BT工具系统动平衡性能比较分析

陈世平1，曾凡宇1，王振振1,李青锋2

(1.重庆理工大学 机械工程学院， 重庆 400054;2.重庆铁马专用车有限公司， 重庆 402246)

不平衡量的存在对机床工具系统在高速旋转下的影响较大。介绍了动平衡的基本概念，基于比较分析的视角，对HSK与BT工具系统动平衡性能从理论方面进行了比较分析，同时进行了数值模拟仿真比较分析。分析结果表明：与BT工具系统相比，HSK工具系统允许的不平衡量更小，所造成的不平衡离心力更小，引起的结构变化更微弱，HSK工具系统高速动平衡性能更好。

HSK工具系统； BT工具系统； 动平衡性能； 比较分析

在高速机床主轴系统中，包括刀柄在内的工具系统形成的不平衡旋转体都会产生离心力，并随着转速的提高离心力迅速增大。离心力会造成切削振动和噪声，影响工件加工的表面质量，并加快刀具的磨损。因此，在高速主轴设计及工具系统设计中必须充分考虑和解决工具系统的离心力问题[1]，研究分析高速状态下工具系统的动平衡性具有十分重要的意义。Jong-Duk Moon等[2]利用频率动态响应的方法研究了工具系统的不平衡性问题。学者Borisov等[3]通过实验，研究了主轴转速在大于25 000 r/min情况下，主轴的平衡问题。在受到复杂主轴结构和离心力影响的情况下，要求工具系统整体位移形变在0.002 5 mm的变化范围内，才会得到较好的高速加工精度要求。沈春根[4]利用在刀柄一侧集中施加不平衡质点的方法研究了工具系统的动力学特性。

研究发现，以BT工具系统为比较对象，针对HSK工具系统进行动平衡性能比较分析的研究较少。基于这一不足，本文从理论分析的角度出发，利用有限元分析方法，比较分析了BT工具系统与HSK工具系统的高速性能，为进一步研究应用HSK工具系统提供了理论依据。

1 动平衡的基本概念

旋转体的动不平衡是由于其质量中心与回转中心线不重合造成的。质量中心偏离回转中心的量称为不平衡量，可以用下式表示[5]：

φ=r·m

(1)

其中：φ为不平衡量(g·mm)，可在动平衡机上测得；r为偏心距(mm)；m为不平衡质量(g)。

就旋转刀具和刀柄来说，目前由于国内外尚无统一的刀具平衡标准。世界各国和机床厂家采用的标准也不一样，往往借用旋转体平衡的国际标准ISO1940—1。在该标准里，用G参数作为平衡等级指标，G后面的数字表示在一定转速下单位旋转体质量允许的残余不平衡量，其单位为g·mm/kg。G参数的数字量分级从G0.4～G4000，数字越小，平衡质量等级越高[6-7]。

根据ISO1940—1的G等级标准，允许的不平衡量U(g·mm)可用下式表示[7]：

(2)

其中：U为允许的不平衡量(g·mm)；G为平衡等级指标(g·mm /kg)；M为旋转体装配质量(kg)；n为旋转体转速(r/min)。

例如：已知工具系统的质量M=1 000 g，确定的平衡质量等级为G6.3，转速为n=18 000 r/min，在此条件下允许的不平衡量为：

另一方面，工具系统在以角速度ω旋转时，不平衡量产生的不平衡离心力可表示为[8]：

F=m·r·ω2

(3)

其中：F为不平衡离心力(N)；r为不平衡量偏心距(mm)；m为不平衡质量(g)；ω为角速度(rad/s)。

结合式(1)(2)(3)可以发现，允许的不平衡量U、角速度ω与不平衡离心力F之间有着密切的联系，结合牛顿第二定律，可以表示为[11]：

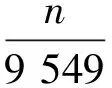
(4)

由式(4)可以看出：在允许的不平衡量U保持一定的条件下，随着转速n增加，不平衡离心力F会成倍增大。又由于不平衡离心力F的存在，势必会造成一定的不平衡振动，根据机械系统动力学基本定律，可以将不平衡量对x，y方向造成的振动表示为[9-10]：

Mx″+Cx′+kx=mrω2cosφ

My″+Cy′+ky=mrω2sinφ

(5)

其中：M为旋转体装配质量(kg)；C为阻尼系数；k为系统刚度(N/m)；m为不平衡质量(g)；ω为角速度(rad/s)。

由式(5)可以得出：工具系统的振动在其他条件保持不变的条件下，不平衡质量m、不平衡量偏心距r、角速度ω的增大都会造成系统振动的增加，从而影响工具系统的高速性能。

2 HSK与BT工具系统动平衡性理论分析

工具系统主要是指主轴、刀柄、夹紧机构等，其核心是刀柄与主轴的配合。传统普通切削加工中BT工具系统发挥了不可替代的作用，其主要特点是刀柄/主轴为7∶24锥度配合，BT刀柄为实心结构。随着技术的发展，这样的结构特点不再适应于高速切削。以空心刀柄HSK为代表的高速工具系统相继出现，它的主要特点为刀柄/主轴为1∶10锥度配合。

现以HSK-A32与BT40两种型号的工具系统为研究对象，进一步探讨允许的不平衡量U、不平衡离心力F、主轴转速n三者之间的关系，从而比较 HSK与BT工具系统动平衡性能的优劣情况。

2.1 允许不平衡量U与转速n的关系

根据上文中的式(2)进行计算。平衡等级精度G的选择，是根据机床和旋转部件的平衡等级要求来进行确定。一般来说，G6.3就能达到较好的平衡精度等级[11]，此处将以此为计算依据。对于旋转体装配质量M来说，比较容易确定，HSK-A32刀柄-刀具的装配质量约为300 g，BT40刀柄-刀具的装配质量约为1 000 g。于是可以通过改变转速来得到主轴转速n与允许的不平衡量U之间的关系。经过计算得到数据后，进行曲线拟合，得到U-n关系曲线，如图1所示。

图1 U-n关系曲线

图1中，实线表示BT工具系统的U-n关系变化趋势，虚线为HSK工具系统的U-n关系变化变化趋势。对曲线进行分析可以得到以下结论：

1) 随着转速的增加，两种工具系统允许的不平衡量U皆呈现下降的趋势，并且当超过15 000 r/min后，两种工具系统允许的不平衡量皆小于5 g·mm。由此说明，达到高转速后，允许的不平衡量U应当更小，才能保证工具系统的使用效果。

2) HSK工具系统允许的不平衡量U，在高低转速下几乎都在5 g·mm以下，变化幅度小。BT工具系统允许的不平衡量U始终要大于HSK工具系统，而且在高低转速下的变化幅度非常明显，几乎相差20 g·mm。由此说明，相对BT工具系统而言，HSK工具系统不平衡量要求能更好地满足高速旋转的要求。

2.2 离心力F与转速n的关系

下面进一步讨论不平衡离心力F与主轴转速n之间的关系，从而比较两种工具系统的动平衡性能。根据上文中的式(4)进行数据的计算，通过改变转速后将计算出的数据拟合出不平衡离心力F与转速n之间的关系曲线，如图2所示。

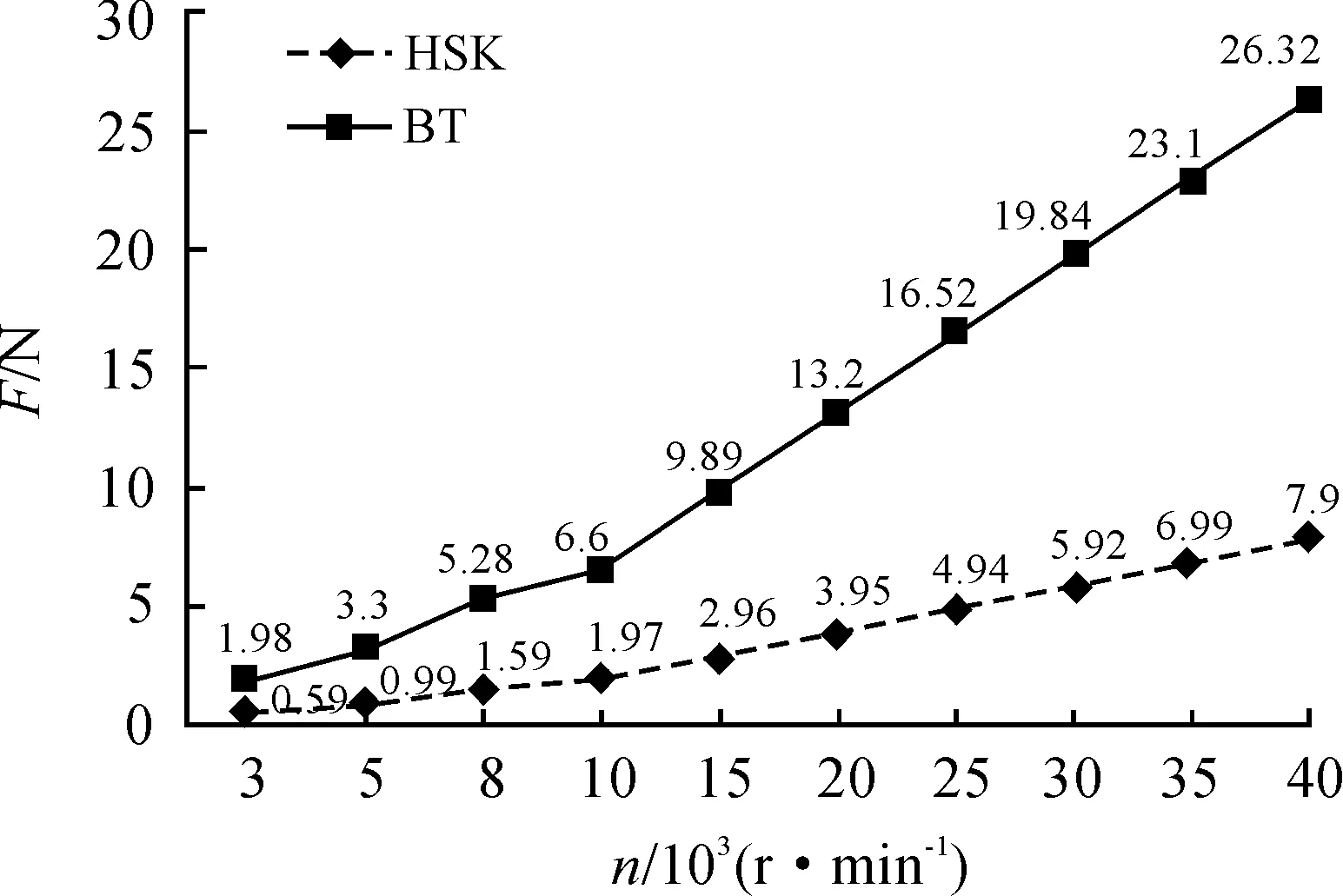
图2 F-n关系曲线

图2中，实线表示BT工具系统的F-n关系变化趋势，虚线为HSK工具系统的F-n关系变化趋势。对曲线进行分析可以得到以下结论：

1) 随着转速的增加，两种工具系统产生的不平衡离心力皆呈上升趋势，但BT工具系统变化更加明显，而HSK工具系统的变化相对缓慢。

2) 在相同转速下，BT工具系统产生的不平衡离心力皆高于HSK工具系统，并且随着转速的增加，二者之间的差距逐渐增大。由此可见，在高速切削条件下，具有较大不平衡离心的BT工具系统所产生的不平衡振动也将大于HSK工具系统，因此，HSK工具系统的动平衡性能优于BT工具系统。

3 HSK与BT工具系统动平衡性数值模拟仿真

从上文的分析可知：不平衡量一定会造成高速下的额外不平衡离心力，从而使工具系统产生不平衡振动，进一步影响其高速性能。而对于工具系统本身来说，不平衡离心力也会造成工具系统结构的应力变化。为说明这种变化的特点，本文基于NX Nastran仿真平台，在主轴与刀柄配合锥面上，为便于比较分析，于HSK与BT刀柄上皆集中施加不平衡质点5 g，取质点所在径向截面上的圆周一圈形成函数曲线，并赋予高低两种转速，并以此来分析不平衡离心力对结构造成的应力变化，借此来分析两种工具系统的动平衡性能。此处值得说明的是：刀柄在出厂后皆经过平衡去重来保证刀柄的平衡，本文中为便于研究工具系统的动平衡性能，采用集中施加不平衡质点的方法来进行实验验证。

3.1 HSK工具系统数值模拟仿真

模拟在工作情况下对HSK工具系统进行边界条件的约束，在此基础上于HSK刀柄上施加5 g的不平衡质点，赋予30 000 r/min与8 000 r/min的主轴转速，选择质点所在径向截面上的圆周一圈，可以得到应力变化函数曲线如图3所示。

图3中，横坐标表示选取点的步长，纵坐标表示该点的应力大小。红色曲线表示转速为30 000 r/min时，施加了5 g的不平衡质点后，该点所在圆周的应力变化。蓝色曲线表示转速为8 000 r/min时，施加了5 g的不平衡质点后，同一处圆周的应力变化。对曲线进行分析可以得到以下结论：

1) 就整体应力大小来看，无论转速的高低，应力始终围绕15 MPa左右上下波动，且接近于一条直线，整体小于25 MPa。但存在一定的应力波动现象，这可能是由于集中施加了不平衡质点以及HSK刀柄空心薄壁的结构特点而造成的正常变化。这样的现象可以说明不平衡质点对HSK工具系统来说，无论转速的大小，不平衡质点对结构的影响都存在。

2) 就应力增加的幅度来看，由于不平衡质点的存在，虽然高低转速下皆存在应力波动变化，但是增加的幅度却并不大，非常微弱仅接近0.5 MPa。这样的现象表明，HSK工具系统的动平衡性能在高低转速下具有一致性，并不会因为转速的增加而出现比较明显的结构变形，从而引起剧烈振动，最终导致动平衡性能下降。

图3 HSK工具系统质点所在圆周的应力变化

3.2 BT工具系统数值模拟仿真

用同样的方法模拟工作情况下对BT工具系统进行边界条件约束后，在BT刀柄上同样施加5 g的不平衡质点，赋予30 000 r/min与8 000 r/min的主轴转速，选择质点所在径向截面上的圆周一圈，可以得到应力变化函数曲线如图4所示。

图4中，横坐标表示选取点的编号，纵坐标表示点对应的应力大小。红色曲线表示转速为 30 000 r/min时，施加了5 g的不平衡质点后，该点所在圆周的应力变化。蓝色曲线表示转速为 8 000 r/min时，施加了5 g的不平衡质点后，同一处圆周的应力变化。对曲线进行分析可以得到以下结论：

1) 就整体应力大小来看，一方面，在转速为 8 000 r/min的条件下，尽管施加了不平衡质点，但BT刀柄的结构应力变化几乎为一条直线，大小约为2.98 MPa； 另一方面，当转速提升至高速 30 000 r/min后，结构应力迅速增加到了37 MPa附近，且波动比较明显。这样的现象可以说明，由不平衡质点所产生的不平衡离心力对BT刀柄的影响非常明显。

2) 就应力增加的幅度来看，施加不平衡质点后，高低转速下应力增加的幅度比较大，接近 30 MPa。这样的现象表明：BT工具系统的动平衡性能在高低转速下并不一致。在低速下尽管有不平衡量的影响，但结构比较稳定，变形不大。但在高速下，结构有明显变形的可能，这将会引起较大的振动。相应地，动平衡性能也会下降。

图4 BT工具系统质点所在圆周的应力变化

3.3 两种工具系统仿真实验比较分析

对两种工具系统施加不平衡质点后，在高低不同的转速下得到实验仿真数据，进行比较可以得到以下几点结论：

1) 就整体应力大小来看，在低速下，HSK刀柄上的应力始终围绕15 MPa左右波动，整体小于25 MPa，而BT刀柄受到不平衡的影响更小，几乎为一条直线；在高速下，HSK刀柄受到的不平衡影响与低速下几乎相一致，而BT刀柄变化却十分明显，结构应力的变化迅速增大至37 MPa左右。这种变化说明，HSK工具系统即使受到不平衡质点的影响，但依然能够保持较好的结构稳定性。但是，本就不具备较好高速性能的BT工具系统，又在高速下受到不平衡质点的影响，所得到的结构应力则呈现较大的变化。

2) 就应力增加的幅度来看。对HSK工具系统来说，高低转速下，应力增加的幅度相接近，约为0.5 MPa，表明了HSK工具系统的动平衡性能在高低转速下的一致性，并不会因为转速的增加，而出现明显的变化。而对BT工具系统来说，应力增加的幅度却较大，接近于30 MPa，表明随着转速的增加，不平衡造成的影响会逐渐增大，并会引起较大的振动，从而影响其动平衡性能。

4 结论

通过理论分析和数值模拟仿真分析，对HSK及BT两种工具系统进行动平衡性能的比较分析，可以得到以下两点结论：

1) 通过理论分析，BT工具系统允许的不平衡量U，无论在何种转速下，皆大于HSK工具系统。相应地，于不平衡离心力F来说，BT工具系统皆高于HSK工具系统，所造成的振动也就更大。

2) 通过数值模拟仿真分析，来验证不平衡离心力将会对结构造成的应力变化。结果表明，受到不平衡量的影响后，HSK工具系统结构应力的变化在高低转速下几乎一致，且较小； 而BT工具系统的结构应力变化，在高低转速下变化非常明显。

综上所述，HSK工具系统动高速平衡性能比BT工具系统更好。

[1] 王贵成，王树林，董广强.高速加工工具系统[M].北京：国防工业出版社，2005.

[2] JONG-DUK M,BONG-SUK K,SOO-HUN L.Development of the active balancing device for high-speed spindle system using influence coefficients[J].International Journal of Machine Tools & Manufacture,2006,46:978-987.

[3] BORISOV A A，MASLOV A R.Small auxiliary tool for milling complex surfaces[J].Russ Enginering,2013，33(7):441-444.

[4] 沈春根.高速加工工具系统的动力学特性及其应用基础研究[D].镇江:江苏大学，2011.

[5] 谢黎明.高速旋转刀具系统动平衡技术的研究[J].组合机床与自动化加工技术，2006，1：29-31.

[6] 陈世平，罗辑，石军.高速切削刀具系统动平衡技术研究[J].现代制造工程，2003，12：55-56.

[7] 钱建强.高速切削刀具系统的不平衡计量和动平衡[J].装备制造技术，2016,1:225-227.

[8] 陶德飞，郑登升，陈建.高速HSK液压夹头及工具系统的不平衡响应[J].制造业自动化，2015，4：88-90,101.

[9] 张义民.机械振动[M].北京：清华大学出版社，2007.

[10] 张国军.高速切削HSK工具系统失效机理与工作可靠性研究[D].沈阳：东北大学，2011.

[11] 张伯霖.高速切削及应用[M].北京：机械工业出版社，2003.

ComparativeAnalysisofDynamicBalanceBetweenHSKandBTToolSystem

CHEN Shiping1, ZENG Fanyu1, WANG Zhenzhen1, LI Qingfeng2

(1.College of Mechanical Engineering, Chongqing University of Technology, Chongqing 400054, China; 2. Chongqing Tiema Special Vehicle Company，Chongqing 402246, China)

The existence of unbalance quantity has a great influence on the tool system in high speed rotation. The basic theoretical of dynamic balance was introduced. Based on the comparative analysis, theoretical of dynamic balance performance of HSK and BT tool system was compared and analyzed. And the numerical simulation was analyzed. The result indicated that compared with the BT tool system, smaller amount of imbalance can HSK tool system allowed, and it had a smaller centrifugal force caused by the imbalance, and had a weaker structural change which caused by unbalanced centrifugal force. HSK tool system shows a better dynamic balance performance.

HSK tool system；BT tool system； dynamic balance performance；comparative analysis

2017-09-04

重庆理工大学研究生创新基金项目资助(YCX2016223)

陈世平(1962—)，男，重庆人，教授，主要从事高速切削加工方面研究，E-mail：chenshiping@cqut.edu.cn。

陈世平，曾凡宇，王振振，等.HSK与BT工具系统动平衡性能比较分析[J].重庆理工大学学报(自然科学)，2017(12):78-82,115.

formatCHEN Shiping, ZENG Fanyu, WANG Zhenzhen,et al.Comparative Analysis of Dynamic Balance Between HSK and BT Tool System[J].Journal of Chongqing University of Technology(Natural Science)，2017(12):78-82,115.

10.3969/j.issn.1674-8425(z).2017.12.013

TG701

A

1674-8425(2017)12-0078-05

(责任编辑何杰玲)