基于ABC-BP的土壤侵蚀量预报模型研究
2018-01-08王权威
王权威,唐 莉
(太原理工大学水利科学与工程学院,山西太原030024)
基于ABC-BP的土壤侵蚀量预报模型研究
王权威,唐 莉
(太原理工大学水利科学与工程学院,山西太原030024)
以预测土壤冲刷量为目标,根据《中国河流泥沙公报》数据资料,建立了以土壤类型、地形、坡度、植被、降雨为输入因子,土壤侵蚀量为输出因子,拓扑结构为5-7-1的BP神经网络预测模型。针对BP神经网络模型缺陷,采用了人工蜂群算法(ABC)对BP神经网络的权值和阈值进行优化,建立了ABC-BP模型,并对该模型的性能进行了验证。结果表明,所建立的ABC-BP土壤侵蚀量预报模型模拟值与实测值的相关系数、平均相对误差分别为0.994 2和4.13%,两者之间无显著的统计学差异,具有较好的一致性和较高的模拟精度。
水土流失;土壤侵蚀量;t检验;人工蜂群算法;BP神经网络模型
0 引 言
土地是维系人类繁衍生息的基本资源,严重的水土流失问题会导致土壤养分流失[1]、沟壑面积增多和农田破坏严重[2]、河床淤积和河道抬高[3]等诸多问题,阻碍了经济社会的可持续性发展。因此,开展水土流失机理、防治和预报等方面的研究工作有极其重要的现实意义。目前,诸多学者围绕水土流失问题展开了大量的研究工作,取得了一定的研究成果。在水土流失机理方面,降雨是径流产生的必要条件和水土流失的原动力[4],坡度和坡形对产流的影响极为显著[5]。不同的植被类型和植被覆盖度对坡面产流及水土流失的影响极为重要,主要表现在拦截降雨和入渗方面[6]。有学者指出,不同土壤类型的坡面产流特性存在明显差异[7],如相同试验条件下,褐土的坡面径流量要高于棕壤土[8]。耕作措施对水土流失的影响也有相关报道。与横厢耕作措施相比,纵厢耕作措施的水土流失问题更加严重[9];与常规耕作比较,深松覆盖处理能有效减少径流和土壤流失,少耕仅仅能减少土壤流失[10]。水土流失预测方面,目前采用的方法主要包括一些经验模型和物理模型[11]。土壤侵蚀预测模型研究多集中于小流域尺度范围[12-15],大尺度范围的预测工作相对较少,并多以遥感和GIS技术为主[16-18]。
人工智能算法的预报方法将为大尺度范围的土壤侵蚀预测工作提供重要的科学依据和全新的研究手段,但采用该方法进行大尺度范围的土壤侵蚀预测工作相对较少。前人在使用神经网络模型进行小尺度土壤侵蚀预测时,部分模型的输入端常常忽略了一些重要因素,主要包括植被覆盖程度、土质因素、降雨等。目前,这些模型所适用的范围相对较小,对全国范围内土壤冲刷量预测研究有待进一步深入。前人在构建此类模型时,一般均采用传统的神经网络算法,在使用过程中会存在搜索空间大、易陷入局部极值点等问题,限制了实际预测中的广泛应用。因此,对该模型的优化改进是十分必要的。人工蜂群算法(ABC)作为一种模拟蜜蜂蜂群智能搜索行为的生物智能优化算法,由于其控制参数少、易于实现和计算简洁,从而成为学术界研究的焦点[19]。目前,基于ABC优化后的BP神经网络模型在水土流失方面的预测还未见报道。本文旨在构建基于ABC优化后的BP神经网络模型(ABC-BP模型),以实现土壤侵蚀量的准确预报,为水土流失预测工作提供技术支持。
1 基本原理
1.1 BP神经网络模型
1968年,以Rumelhart和McCelland为首的科学家小组首次提出了BP神经网络,它是目前模拟精度相对较高、应用范围最广的神经网络模型之一,由输入层、隐含层、输出层3部分构成。图1为BP神经网络的工作原理和基本网络结构。图中,m、q和n分别为输入层节点、隐含层节点和输出层节点。误差反向传播算法的学习过程由信息的正向传播和误差的反向传播2个过程组成。外界的输入信息首先由输入层接收,并传递给中间层神经元,然后经过中间层的信息处理后,最终传输给输出层,并由输出层向外界输出信息。当输出信息与期望不吻合时,便进入误差反向传播机制,各层间的权值矩阵和阈值矩阵进行不断调整,如此反复直至达到期望要求为止。

图1 BP神经网络基本结构及工作原理
1.2 ABC流程
在ABC中,人工蜂群主要由采蜜蜂、观察蜂和侦察蜂3个组成部分。在蜂群进化过程中,前2个负责执行开采过程,后者执行探索过程。ABC的实现步骤及具体过程如下:
(1)随机产生SN(蜂群规模)个初始解,将其中一半与采蜜蜂对应,并计算各个解的适应度值,将最优解记录下来。
(2)设置循环数Cycle=1。
(3)采蜜蜂进行邻域搜索产生新解vij,计算其适应度,并对原蜜源位置xij和新解vij进行贪婪选择,即
vij=xij+φij(xij-xkj)
(1)
式中,k为不同于i的蜜源;φij为[-1,1]之间的随机数,控制着原蜜源位置xij邻域内蜜源位置的产生。候选位置形象地代表着原蜜源位置xij与邻域内随机的一个蜜源xkj之间的对比关系。
(4)计算与xi相关的选择概率Pi,即
(2)
式中,fiti为xi的适应度值,i=1,2,…,SN。
(5)观察蜂根据轮盘赌选择法,以概率Pi选择食物源,并根据式(1)进行邻域搜索产生新解,计算适应度,并对xij和vij进行贪婪选择。
(6)判断是否有要放弃的解,如果存在,则采用式(3)进行搜索产生1个新解替代旧解,即
(3)

(7)记录迄今为止最好的解。
(8)Cycle=Cycle+1,若Cycle<最大循环次数MCN,则转(3);否则,输出最优结果。
2 ABC-BP神经网络模型的构建
2.1 ABC初始值
本文选取的蜂群大小为200个,极限值limit需要大于每个解的维数D,可表示为
D=Nmin×Nhidden+Nhidden+Nhidden×Noutput+Noutput
(4)
式中,Nmin、Nhidden、Noutput分别是神经网络的输入层、隐含层、输出层的神经元个数。初始解是随机产生的(-1,1)之间的数,计算得到D值为50。
2.2 神经网络输入输出层的确定
结合前人研究现状,水土流失的关键影响因素可归结为土壤类型、地形、坡度、植被和降雨等。因此,本研究将上述5项作为该模型的输入项,土壤侵蚀量作为模型的输出项。本研究的数据主要来源于《中国水土保持公报》,经过整理得到全国不同水土流失典型监测点的土壤侵蚀量资料,资料分别来自东北黑土区、北方山地丘陵区、西北黄土高原、南方红壤区、西南紫色土区、西南岩溶区和青藏高原区。部分数据资料见表1。总样本数为194个,以7∶3的比例将该样本分为训练集和预测集,即样本数分别为136个和58个。

表1 基础样本资料
2.3 神经网络结构的确定
隐含层数目与模拟精度呈正比,但过多的隐含层也可能会造成模型过于复杂等问题,通常选择单隐含层为宜。隐含层节点数可以根据相关的经验方法进行确定。首先根据式(5)确定节点数大致范围为4~12,通过多次试算从而确定最优节点数。为保证BP 神经网络模型的非线性,从输入层到隐含层的信息传递采用logistic函数,隐含层到输出层信息传递采用purlin 函数,神经网络的训练采用trainlm 函数。训练目标误差为0.000 1,最大训练次数为5 000次,即

(5)
式中,q为隐含层节点数;m为输入层节点数;n为输出层节点数;a为1~10之间的整数。
3 结果分析
3.1 最优隐含层节点的确定
图2为不同节点数条件下神经网络模型精度。从图2可以看出,当隐含层节点数增加时,神经网络模型模拟值与实测值的平均相对误差MAPE和均方根误差RMSE均呈现先逐渐减小,然后逐渐增大的变化趋势。在多次试算中,当隐含层节点数为7时,经过2 384次训练后,模型的训练误差为0.000 1,能够达到模型的训练精度要求。因此,认为7为合理的节点数。综上所述,本研究中模型的拓扑结构为5-7-1。

图2 不同节点数条件下神经网络模型精度
3.2 训练组模拟效果
图3为冲刷量实测值与预测值的相关关系。从图3可以看出,BP模型和ABC-BP模型的预测值和实测值构成的线性拟合模型的拟合度分别达到0.994 0和0.997 1,方程的斜率分别为0.999 4和0.999 8,说明这2种模型的预测值与实测值之间均具有较强的线性相关性,并且预测值与实测值之间能够保持较好的一致性。图4为各个样本的相对误差。从图4可知,BP模型和ABC-BP模型预测值与实测值间的最大相对误差分别为7.56%和9.12%,最小分别为0.003%和0.439%,平均分别为3.42%和5.24%。可以看出,ABC-BP模型的训练误差明显更小。此外,本文采用统计学方法对模型预测值与实测值之间的差异性进行了统计学分析,分析结果见表2。从表2可以看出,t值的绝对值小于t检验临界值,即|t| 图3 冲刷量实测值与预测值相关性 图4 样本相对误差 方法自由度t检验临界值显著性结果ABC-BP135-0.2910.771BP135-0.2290.819 图5为冲刷量实测值与预测值的相关关系。从图5可以看出,BP模型和ABC-BP模型的预测值与实测值构成的线性拟合模型的拟合度分别达到0.988 8和0.994 2,方程的斜率分别为1.007 4和1.007 3,说明2种模型的预测值与实测值之间均具有较强的线性相关性,并且预测值与实测值之间能够保持较好的一致性。图6为各个样本的相对误差。从图6可知,ABC-BP模型和BP模型实测值与预测值之间的最大相对误差分别为7.37%和9.36%,最小分别为0.13%和3.33%,平均分别为4.13%和6.43%,ABC-BP模型具有更高的预测精度。表3为样本的实测值与模拟值间的统计学差异性分析结果。经计算,实测值与预测值之间并无显著的统计学差异。综上所述,2种模型均可满足模拟预报精度要求,相对而言,ABC-BP模型的预测效果更优。 图5 冲刷量实测值与预测值相关性 图6 样本相对误差 表3 实测值与预测值t配对检验结果 本文将人工蜂群算法(ABC)与BP 神经网络相结合,建立土壤侵蚀量预报模型,把求解BP 神经网络各层权值、阀值的过程转化为蜜蜂寻找最佳蜜源的过程,以全国不同水土流失典型监测点的土壤侵蚀量资料作为研究样本,构建了ABC-BP土壤侵蚀量预报模型。ABC-BP模型训练组的平均相对误差为3.42%,训练效果均优于BP模型;预测组的平均相对误差为4.13%,预测效果均优于BP模型。ABC-BP土壤侵蚀量预报模型可以实现全国水土流失典型监测点土壤冲刷量的准确预报。 中国的水土流失具有较为明显的时空动态分布特征,将水土流失监测点的地域位置信息及随时间的演变特征融入黑箱模型,以实现全国水土流失的时空动态演变还有待进一步深入研究。此外,多种预测模型的相互结合以及模拟算法的改进,也是进一步的研究方向。 [1] 赵心畅, 徐洪霞. 溧阳抽水蓄能电站水土流失防治措施的分析[J]. 水力发电, 2010, 36(7): 22- 24. [2] 高照良, 穆兴民. 黄土水蚀风蚀交错区土地利用/覆被时空变化研究——以陕西省神木县六道沟流域为例[J]. 水土保持学报, 2004, 18(5): 146- 150. [3] 张洪江, 吴发启, 胡春元, 等. 土壤侵蚀原理[M]. 北京: 中国林业出版社, 1999. [4] 金雁海, 柴建华, 朱智红, 等. 内蒙古黄土丘陵区坡面径流及其影响因素研究[J]. 水土保持研究, 2006, 13(5): 292-295, 298. [5] 吴星鑫, 陆宝宏, 赵超, 等. 降雨径流预报方案的设计研究[J]. 水力发电, 2014, 40(7): 18-21, 56. [6] 喻定芳, 戴全厚, 王庆海, 等. 北京地区等高草篱防治坡耕地水土流失效果[J]. 农业工程学报, 2010, 26(12): 89- 96.[7] 徐永年, 苏晓波, 王向东, 等. 绿化植生带在不同坡面上的水土保持效果[J]. 水利水电技术, 2002, 33(7): 62- 64. [8] 王志伟, 艾钊, 张国庆, 等. 沂蒙山区坡面侵蚀过程[J]. 中国水土保持科学, 2013, 11(5): 42- 47. [9] 金轲, 蔡典雄, 吕军杰, 等. 耕作对坡耕地水土流失和冬小麦产量的影响[J]. 水土保持学报, 2006, 20(4): 1- 5, 49. [10] 菊燕宁, 张壮志. 水电站建设中新增水土流失预测及防治措施研究[J]. 水利水电技术, 2015, 46(9): 128- 134. [11] RENARD K G, FOSTER G R, WEESIES G A, et al. RUSLE: Revised universal soil loss equation[J]. Journal of soil and Water Conservation, 1991, 46(1): 30- 33. [12] 洪华生, 杨远, 黄金良. 基于GIS和USLE的下庄小流域土壤侵蚀量预测研究[J]. 厦门大学学报: 自然科学版, 2005, 44(5): 675- 679. [13] 蔡崇法, 丁树文, 史志华, 等. 应用USLE模型与地理信息系统IDRISI预测小流域土壤侵蚀量的研究[J]. 水土保持学报, 2000, 14(2): 19- 24. [14] 段军彪, 景旭, 上官周平. 基于遗传算法的BP网络在小流域侵蚀量预测中的应用[J]. 西北农业学报, 2008, 17(2): 317- 320. [15] 胡亚萍, 董贝贝, 姜宏立, 等. SVR与BP神经网络对小流域次降雨侵蚀产沙预测结果的比较[J]. 北方环境, 2013, 29(1): 114- 117. [16] 杨胜天, 程红光, 步青松, 等. 全国土壤侵蚀量估算及其在吸附态氮磷流失量匡算中的应用[J]. 环境科学学报, 2006, 26(3): 366- 374. [17] 祝赢, 章文波, 刘素红, 等. 第一次全国水利普查侵蚀模数的批量计算方法——基于CSLE和GIS的土壤水蚀模数计算器设计与应用[J]. 水土保持通报, 2012, 32(5): 291- 295. [18] 赵晓丽, 张增祥, 刘斌, 等. 基于遥感和GIS的全国土壤侵蚀动态监测方法研究[J]. 水土保持通报, 2002, 22(4): 29- 32. [19] 秦全德, 程适, 李丽, 等. 人工蜂群算法研究综述[J]. 智能系统学报, 2014, 9(2): 127- 135. StudyonSoilErosionPredictionModelBasedonArtificialBeeColonyAlgorithmandBPNeuralNetwork WANG Quanwei, TANG Li (School of Hydraulic Science and Engineering, Taiyuan University of Technology, Taiyuan 030024, Shanxi, China) Taking the prediction of soil erosion amount as a goal, a BP neural network model with a topological structure of 5-7-1 is established according to the data from the Bulletin of River Sediment in China. In the model, the soil type, topography, slope, vegetation and rainfall are taken as input data and the soil erosion amount is taken as output. In view of the shortages of BP neural network method, the weight value and threshold value of BP neural network are optimized by using Artificial Bee Colony algorithm, and then the simulation effect of ABC-BP model is analyzed. It shows that the correlation coefficient and average relative error between simulation value and measured value are 0.9942 and 4.13% respectively. The ABC-BP neural network model has perfect consistency and higher prediction precision. soil and water loss; soil erosion amount; t-test; Artificial Bee Colony algorithm; BP neural network model S157 A 0559- 9342(2017)09- 0001- 04 2017- 03- 02 国家自然科学基金资助项目(51509176) 王权威(1992—),男,山西吕梁人,硕士研究生,主要从事水文及水资源研究;唐莉(通讯作者). (责任编辑杨 健)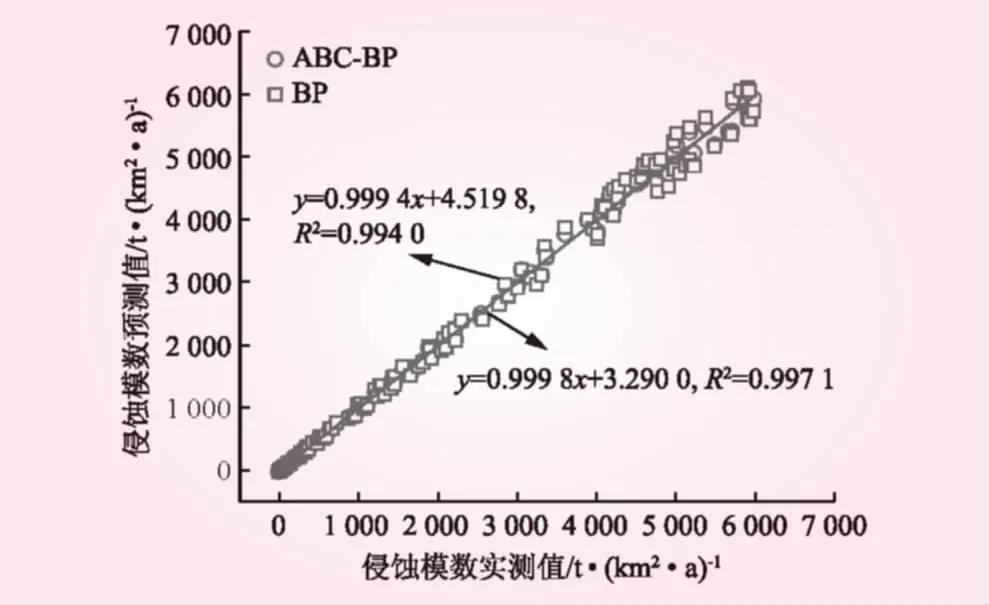


3.3 预测组模拟效果



4 结 语

