一种求解厌恶型p-中位问题的混合进化算法
2018-01-08林耿闽江学院数学系福建福州350108
林耿(闽江学院 数学系, 福建 福州 350108)
一种求解厌恶型p-中位问题的混合进化算法
林耿
(闽江学院 数学系, 福建 福州 350108)
厌恶型p-中位问题是一个NP-困难问题.提出了一种求解厌恶型p-中位问题的混合进化算法.首先,通过贪心随机自适应搜索方法和随机构造方法产生初始种群.然后,利用搜索过程中收集到的全局信息和局部信息构造新解,期间注意提高搜索的多样性,避免早熟.最后,针对厌恶型p-中位问题的特点,构造基于约束交换邻域的局部搜索算法,提高了算法的局部搜索能力.通过求解72个标准测试例子以检验算法的性能,发现该算法在较短时间内得到了高质量解,优于现有算法.
厌恶型p-中位问题;进化算法;分布估计算法;局部搜索;启发式算法
0 引 言
选址问题(facility location problem)是运筹学研究的重要内容之一,在运输、教育、通信网络、管理等学科中有广泛应用.近年来,随着工业化的发展,环境污染已成为严峻的社会问题;同时,人们的环保意识越来越强,政府对厌恶型设施选址问题越来越重视.所谓厌恶型设施是指污染环境、危害或具有潜在危害人们身心健康可能性的设施,比如核电站、垃圾处理站、化工厂、手机基站发射塔等.这些厌恶型设施大多是社会必需的公共设施,但人们期望尽量远离这些设施.厌恶型设施选址问题已经成为学者们广泛关注的热点之一.
根据不同的问题背景,可以建立不同的厌恶型设施选址模型[1-5].目前,很多模型是基于某一类特殊情况或者特殊图的.2007年,根据厌恶型设施的选址应尽可能远离顾客的要求,BELOTTI等[5]建立了一般图的厌恶型p-中位问题(obnoxiousp-median problem).厌恶型p-中位问题是指在一般图的顶点上确定p个点来布置厌恶型设施,使所有顾客到达这些厌恶型设施的最小距离总和最大.因此,求解一般图上的厌恶型p-中位问题具有重要的理论和现实意义.
厌恶型p-中位问题是一个NP-困难问题,可用0-1线性规划建立数学模型.BELOTTI等[5]提出了基于分支-切割的精确算法(branch-and-cut method,B&C).为了提高算法的效率,B&C法先通过禁忌搜索算法(exploring tabu search,XTS)获得下界,然后再进行分支割算法.数值实验结果表明,B&C法能够在可接受的时间内求解小规模厌恶型p-中位问题,但随着问题规模的增大,求解时间迅速增加,无法在短时间内求解较大规模的问题.故学者们设计了启发式算法来求解大规模厌恶型p-中位问题.COLMENAR等[6]提出了一种求解厌恶型p-中位问题的贪心随机自适应算法(greedy randomized adaptive search procedure,GRASP).该算法首先通过贪心构造算法构造初始解.然后,通过过滤机制找出具有潜力的初始解.最后,通过局部搜索算法进一步提高了具有潜力的解的质量.重复以上步骤,直到算法停止,满足准则.通过72个标准例子测试GRASP,与B&C、XTS相比,GRASP能够较快地找到高质量的解.
虽然,XTS和GRASP在求解速度上有了较大提高,但其求解时间依然会随着问题规模的增大而快速增加.导致算法求解速度慢的主要原因有: 1)没有充分利用先前搜索获得的全局信息和局部信息来构造新解;2)为了保证解的可行性,XTS和GRASP采用基于交换邻域的局部搜索算法.由于交换邻域中解的个数为p(n-p),其中n为设施的数量,随着n的增大,算法的搜索速度急剧下降.
进化算法已经成功应用于求解许多大规模优化问题[7-8].针对现存算法求解速度慢的问题,提出了一种混合进化算法(hybrid evolutionary algorithm,HEA)求解厌恶型p-中位问题.HEA法基于厌恶型p-中位问题的特点,首先利用分布估计算法收集到的全局信息,结合当前精英解集中解的局部信息生成新一代的解向量,使得新产生的解具有较高的质量,以及多样性.然后,采用基于约束交换邻域的局部搜索算法进一步提高求解速度和解的质量.采用72个标准测试例子测试本文算法,并与B&C、XTS和GRASP法进行比较,以证明本文算法的高效性.
1 问题的描述和数学模型
给定一个顾客集合I={1,2,…,m}和设施集合J={1,2,…,n},假设dij表示第i个顾客和第j个设施之间的距离,厌恶型p-中位问题需要寻找一个含有p个设施的子集S⊂J,使得每一个顾客i∈I与选中的p个设施的最小距离的总和最大.引入n维0-1向量x=(x1,x2,…,xn),如果第j个设施被选中,那么xj=1;否则xj=0.则厌恶型p-中位问题可以用以下0-1规划建立数学模型:
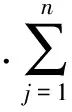
厌恶型p-中位问题是一个NP-困难问题[9].
2 混合进化算法
混合进化算法[10-11]能够克服单种进化算法的缺点,提高搜索效率,已经成功应用于求解许多大规模优化问题.ZHANG等[12]和CHAURASIA等[13]提出了一类将全局信息和局部信息相结合的混合进化算法,能够有效提高算法的搜索效率.受此启发,针对现有算法求解速度慢的问题,根据厌恶型p-中位问题的特点,提出了一种将统计学习方法与进化算法有机结合,能够快速求解厌恶型p-中位问题的混合进化算法(HEA),也称种群算法.算法主要包含4个基本子模块: 1) 初始种群生成方法;2) 概率模型;3) 新解的产生方法;4) 基于约束交换邻域的局部搜索算法.
2.1 初始种群的生成方法

为了更好地介绍改进的COLMENAR等[6]的初始解构造方法(improved constructive algorithm,ICA),先给出一些下文要用到的记号.

(1)
假设S为选中的设施的集合,|S|为选中的设施的数量.ICA初始化S=∅,首先从初始候选集合CL={j∈J:φ(j)≥φmin+λ*(φmax-φmin)}中随机选择一个设施k加入S,其中λ∈(0,1).向S中增加设施,使得目标函数值下降.记g(S,j)为向S中增加设施j后目标函数值的改变量,即
(2)

然后,ICA构造随机候选集合:
RCL={j∈J-S:g(S,j)≥
gmax-λ*(gmax-gmin)}.
(3)
从RCL中随机选择一个设施加入S.ICA重复以上步骤,直到|S|=p.
初始种群生成法的步骤如下:
算法1
步骤1初始化t=1,P=∅.


步骤4由式(2)计算g(S,j),∀j∈J-S,并根据式(3)构造RCL.

步骤6如果|S| 步骤10如果|S| 已有研究[14-15]表明: 大规模组合优化问题的高质量解之间具有很高的相似度.HEA通过概率模型记录先前搜索的高质量解的空间分布情况.引入n维概率向量v=(v1,v2,…,vn),其中vj表示xj=1的概率,即设施j被选中的概率. (4) 更新概率向量,其中0≤κ≤1表示学习速率.由于优势解集解的结构比较接近,为避免早熟,对概率向量进行以下修正: (5) 分布估计算法通过概率模型记录解空间的分布情况,利用概率向量产生下一代的解向量.该方法虽然有效地利用了全局信息.但缺乏对搜索过程中收集到的局部信息的利用,导致算法的局部搜索能力不足. 遗传算法通过对种群中的解进行交叉和变异操作来构造下一代解向量.有效利用了局部信息,但没有充分利用搜索过程中的全局信息,导致算法容易陷入局部最优. HEA结合2种算法的优点构造新的解向量.假设E={z1,z2,…,zμ}是μ个解组成的精英解集,新产生的解向量记为x=(x1,x2,…,xn).首先,HEA从精英解集E中随机选择一个解z=(z1,z2,…,zn).然后,对于新解x的每一维分量xj,HEA可以通过概率模型产生,或直接继承zj的值.最后,由于通过以上方法得到的可能不是可行解,HEA可通过以下方法对解进行修复: 1)如果选中的设施超过p个,则从S中随机删除|S|-p个设施;2)如果选中的设施少于p个,则从J-S中随机选择p-|S|个设施加入S. 新解的产生方法及步骤如下: 算法2 步骤1从E中随机选择一个解z.初始化t=1. 步骤2产生一个随机数θ∈[0,1]. 步骤3如果θ≤0.7,则转步骤4;否则,令xt=zt. 步骤4产生一个随机数θ∈[0,1].如果θ≤vt,则令xt=1;否则,令xt=0. 步骤5令t=t+1,如果t≤n,则转步骤2;否则,转步骤6. 步骤6假设解向量x对应的选中的设施集合为S.如果|S|>p,则从S中随机删除|S|-p个设施.如果|S| 步骤7停止,并将S所对应的解x输出. 局部搜索算法能够有效提高进化算法的局部搜索能力.研究结果表明,进化算法的大部分时间消耗在局部搜索中[16].因此,设计高效的局部搜索算法是进化算法的重要步骤之一. KERNIGHAN等[17]提出了一种高效的迭代改进局部搜索算法(Kernighan and Lin algorithm, KL)以求解图的划分问题.该算法已被应用于求解各类大规模优化问题[18].为了提升局部搜索算法的速度,根据厌恶型p-中位问题的特点,HEA提出了一种基于约束交换邻域的KL算法(constrained swap neighborhood based KL algorithm,CENKLA).该局部搜索算法能够在搜索过程中保持解的可行性. d(S,j)=f(S-{j})-f(S), (6) 其中f(S)表示选中的设施集合为S时的目标函数值.CENKLA分别构造了S和J-S中有潜力且可以自由改变状态的子集Nd⊂S∩Fd和Na⊂(J-S)∩Fa.即 Nd={j∈S∩Fd:d(S,j)≥dmin+ (7) Na={j∈(J-S)∩Fa:g(S,j)≥gmin+ (8) α∈(0,1).令 (9) 输入可行解x0,CENKLA的具体步骤如下: 算法3 步骤1初始化x=x0,xb=x0. 步骤2初始化Fd=S,Fa=J-S,其中S为当前解x选中的设施集合. 步骤3由式(7)和(8)分别构造Nd和Na. 步骤6如果f(x)>f(xb),令xb=x. 步骤7如果Fd=∅或Fa=∅,转步骤8;否则,转步骤3. 步骤8如果f(xb)>f(x0),令x0=xb,x=x0,转步骤2;否则,停止,输出xb. 假设算法的最大迭代次数为G,本文提出的混合进化算法HEA的详细步骤如下: 算法4 步骤2从P中选择μ个最好的解构成精英解集E. 步骤3令x*=argmax{f(x),x∈P},xw为E中最差的解,即xw=argmin{f(x),x∈E}. 步骤4令iter=iter+1.从P中选择ρ个最优解,用式(4)和(5)更新概率向量v.初始化t=1,P′=∅. 步骤5采用新解的产生方法(算法2)产生新的解xt,并用局部搜索算法(算法3)进一步优化.令P′=P′∪{xt}. 步骤6如果f(xt)>f(xw),令E=E∪{xt}-{xw},xw=argmin{f(x),x∈E}. 步骤7如果f(xt)>f(x*),令x*=xt. 步骤10如果iter 为了检测HEA算法的性能,本文用C语言对混合进化算法进行编程.算法的运行环境为Windows 7,CPU 3.4 GHz,内存4 GB. COLMENAR等[6]将OR-library[19]中的24个p-中位问题的测试例子(从pmed17到pmed40)转换为72个厌恶型p-中位问题的测试例子.这72个例子已被应用于测试B&C、XTS和GRASP.本文也将利用这些例子来测试HEA. 利用本文提出的混合进化算法求解72个标准例子.为了避免算法的随机性,在同一台电脑上对每个例子进行20次测试.运行过程中分别记录每个例子在20次测试中得到的最优解、平均解和标准差,以及运行20次需要的平均时间.测试结果如表1所示.表1还给出了现存算法(包括B&C、XTS和GRASP)在每个例子上找到的当前最优解.HEA新找到的最优解在表1中用黑体显示. 从表1的结果可以看出: 1)HEA在17个例子上找到了比当前最优解更好的解.另外,HEA在30个例子上能够找到当前最优解. 2)HEA的标准差变化范围为[0,12.14],平均标准差为3.09.此外,HEA在20个例子中每次都能找到一样的解(即标准差为0).可见,HEA是比较稳健的进化算法. 3)HEA算法的求解时间随着问题规模的增大而增加.72个例子的平均求解时间为50.182 s. 表1 HEA的实验结果Table 1 Experimental results of HEA (续表1) 为进一步检验本文提出的HEA性能,将HEA与现存算法B&C、XTS、GRASP做比较,其中GRASP算法使用2种停止准则.第1种GRASP(1 000)迭代1 000次停止,第2种GRASP(5 000)迭代5 000次停止.表2给出了5种算法在72个例子中运行得到的平均解和平均求解时间.表2中B&C、XTS、GRASP(1 000)和GRASP(5 000)的结果均引自文献[6]. 表2 HEA在测试集上的情况比较Table 1 Comparison of HEA over the whole set of instances 从表2可以看出,HEA得到的平均解优于B&C、XTS和GRASP(1 000),并且求解的平均时间比B&C、XTS和GRASP(1 000)少很多.因此,HEA的性能优于XTS和GRASP(1 000).HEA得到的平均解虽比GRASP(5 000)稍差,但GRASP(5 000)的求解时间远长于HEA.注意: B&C、XTS、GRASP(1 000)和GRASP(5 000)是在i5660 电脑(3.3 GHz,8 G内存)上运行的.根据http: //www.cpubenchmark.net的CPU速度数据报告,i5660 电脑(3.3 GHz,8 G内存)的运行速度是本文算法所用电脑运行速度的1.6倍.所以,HEA的求解速度明显快于XTS和GRASP. 以上的实验和比较结果表明,HEA能够在较短时间内找到高质量的解,是求解厌恶型p-中位问题的有效算法. HEA的2个主要组成模块: 初始种群生成方法记作HEA1,即将HEA中的初始种群生成方法改成随机生成方法而其他模块保持不变的算法;基于约束交换邻域的局部搜索算法记作HEA2,即HEA的迭代过程中去掉基于约束交换邻域的局部搜索算法.为了研究这2个模块对HEA性能的影响,应用HEA1、HEA2和HEA分别求解pmed29-p150,运行结果见图1. 图1 HEA1、HEA2和HEA的运行结果Fig.1 Experimental results of HEA1,HEA2 and HEA 从图1中可以看出,HEA1、HEA2的性能明显比HEA差.HEA采用初始种群生成方法,能够生成具有良好多样性的高质量初始种群,有效提高搜索效率.HEA通过基于约束交换邻域的局部搜索算法提高了算法的搜索能力,可更快地找到高质量解. 针对现存算法求解速度慢的问题,提出了一种求解厌恶型p-中位问题的混合进化算法(HEA).该算法主要由初始种群生成方法、概率模型、新解的产生方法和基于约束交换邻域的局部搜索算法组成.初始种群生成方法通过贪心随机自适应搜索方法产生高质量的解,并采用随机构造算法生成多样性的解.HEA通过概率模型收集了搜索过程中得到的全局信息,并结合精英解的局部信息生成新解.新解既继承了先前局部最优解的优良结构,又具有较好的多样性.最后,构造基于约束交换邻域的局部搜索算法.本算法提高了局部搜索能力,可快速有效提高解的质量.通过72个标准测试例子检验,发现本算法能够在较短时间内找到高质量的解,明显快于B & C,XTS和GRASP. 本文通过概率模型收集全局信息,但该概率模型在搜索到一定程度后,容易使算法收敛.下一步要做的工作是改进概率模型,并将本文算法推广应用于解决其他组合优化问题,比如: 最大二等分问题、集合覆盖问题等. [1] 程郁琨.厌恶型、半厌恶型及候补型p-中位问题[D].上海: 上海大学,2010: 14-52. CHENG Y K.Obnoxious,Semi-obnoxiousandBackupp-MedianProblem[D].Shanghai: Shanghai University,2010: 14-52. [2] 柏春松.半厌恶型、厌恶p-中位问题及具有连通约束的选址问题[D].上海: 上海大学,2014: 51-63. BO C S.Semi-obnoxiousandObnoxiousp-MedianProblemandLocationProblemwithConnectedConstraints[D].Shanghai: Shanghai University,2014: 51-63. [3] BATTA R,LEJEUNEB M,PRASAD S.Public facility location using dispersion,population,and equity criteria[J].EuropeanJournalofOperationalResearch, 2014,234(4): 819-829. [4] FARAHANI R,STEADIESEIFI M,ASGARI N.Multiple criteria facility location problem: A survey[J].AppliedMathematicalModeling,2010,34: 1689-1709. [5] BELOTTI P,LABBE M,MAFFIOLI F,et al.A branch-and-cut method for the obnoxiousp-median problem[J].4OR,2007,5(4): 299-314. [6] COLMENAR J M,GREISTORFER P,MARTI R,et al.Advanced greedy randomized adaptive search procedure for the obnoxiousp-median problem[J].EuropeanJournalofOperationalResearch,2016,252: 432-442. [7] RUIZ E,ALBAREDA-SAMBOLA M,FERNANDEZ E,et al.A biased random-key genetic algorithm for the capacitated minimum spanning tree problem[J].Computers&OperationsResearch,2015,57: 95-108. [8] CEBERIO J,IRUROZKI E,MENDIBURU A,et al.A review on estimation of distribution algorithms in permutation-based combinatorial optimization problems[J].ProgressinArtificialIntelligence,2012,1(1): 103-117. [9] TAMIR A.Obnoxious facility location on graphs[J].SIAMJournalonDiscreteMathematics,1991,2(4): 550-567. [10] PAN Q K,RUIZ R.An estimation of distribution algorithm for lot-streaming flow shop problems with setup times[J].Omega,2012,40(2): 166-180. [11] VIDAL T,CRAINIC T G,GENDREAU M,et al.A hybrid genetic algorithm with adaptive diversity management for a large class of vehicle routing problems with time-windows[J].Computers&OperationsResearch,2013,40(1): 475-489. [12] ZHANG Q,SUN J,TSANG E.An evolutionary algorithm with guided mutation for the maximum clique problem[J].IEEETransactionsonEvolutionaryComputation,2005,9(2): 192-200. [13] CHAURASIA S N,SUNDAR S,SINGH A.A hybrid evolutionary approach for set packing problem[J].Opsearch,2015,52(2): 271-284. [14] LIN G,ZHU W.An efficient memetic algorithm for the max-bisection problem[J].IEEETransactionsonComputers,2014,63(6): 1365-1376. [15] WU Q,HAO J K.Memetic search for the max-bisection problem[J].Computers&OperationsResearch,2013,40(1): 166-179. [16] NERI F,COTTA C.Memetic algorithms and memetic computing optimization: A literature review[J].SwarmandEvolutionaryComputation,2012(2): 1-14. [17] KERNIGHAN B W,LIN S.An efficient heuristic procedure for partitioning graphs[J].BellSystemTechnicalJournal,1970,49(2): 291-307. [18] AMIRI B,HOSSAIN L,CRAWFORD J W,et al.Community detection in detection in complex networks: Multi-objective enhanced firefly algorithm[J].Knowledge-BasedSystems,2013,45: 1-11. [19] BEASLEY J E.OR-library: Distributing test problems by electronic mail[J].JournaloftheOperationalResearchSociety,1990,41(11): 1069-1072. LIN Geng The obnoxious p-median problem is known to be NP-hard.A hybrid evolutionary algorithm is proposed to solve the obnoxiousp-median problem.Firstly,an initial population is generated by a greedy randomized adaptive search procedure and a random constructive procedure.Then,to diversify the search and avoid the premature convergence,the proposed algorithm uses the global information and the local information gathered during the search to generate new solutions.Finally,according to the characteristics of obnoxiousp-median problem,a constrained swap neighborhood based on local search procedure is developed to enhance the exploitation of the algorithm.Seventy two benchmark instances are tested to demonstrate the effectiveness of the algorithm.Experimental results and comparison with the existing algorithms show that the proposed algorithm is able to obtain high quality solutions in significantly less CPU time. obnoxiousp-median problem; evolutionary algorithm; estimation of distribution algorithm; local search; heuristic algorithm 2016-12-05. 国家自然科学基金资助项目(11301255);福建省自然科学基金资助项目(2016J01025);福建省高校新世纪优秀人才支持计划项目. 林耿(1981—),ORCID: http: //orcid.org/0000-0002-1643-6859,男,博士,副教授,主要从事优化理论与算法、智能计算等研究, E-mail: lingeng413@163.com. 10.3785/j.issn.1008-9497.2018.01.006 O 224; TP 301.6 A 1008-9497(2018)01-029-08 Ahybridevolutionaryalgorithmforsolvingtheobnoxiousp-medianproblem.Journal of Zhejiang University (Science Edition),2018,45(1): 029-036




2.2 概率模型
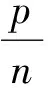

2.3 新解的产生方法
2.4 基于约束交换邻域的局部搜索算法

α*(dmax-dmin)},
α*(gmax-gmin)},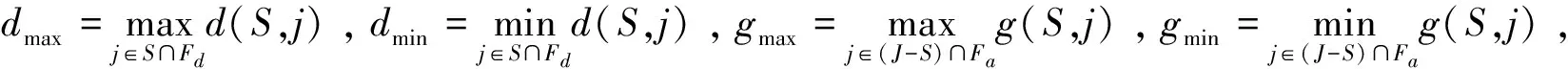


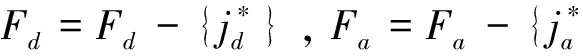
2.5 HEA算法步骤


3 实验结果与分析
3.1 标准测试例子
3.2 参数设置

3.3 结果与比较



3.4 主要模块对HEA性能的影响分析
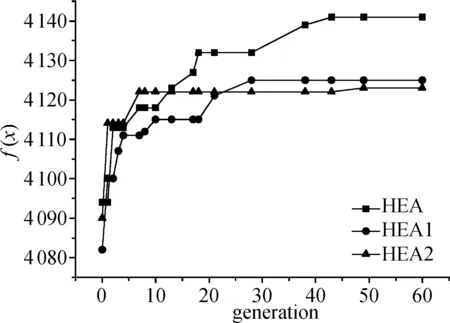
4 结 语
(DepartmentofMathematics,MinjiangUniversity,Fuzhou350108,China)
