一类大气混沌模型的动力学分析及数值仿真

张勇，杨雪玲，舒永录(.河南工业职业技术学院 基础教学部， 河南 南阳 47000； .河南工业职业技术学院 汽车工程学院，河南 南阳 47000； .重庆大学 数学与统计学院， 重庆 40)

一类大气混沌模型的动力学分析及数值仿真

张勇1，杨雪玲2，舒永录3
(1.河南工业职业技术学院 基础教学部， 河南 南阳 473000； 2.河南工业职业技术学院 汽车工程学院，河南 南阳 473000； 3.重庆大学 数学与统计学院， 重庆 401331)

基于已有文献以及微分方程与动力系统的基本理论与方法，采用解析方法推导了一类大气混沌模型的全局吸引域和最终界，并对此模型进行了仿真.数值仿真表明了理论分析结果的正确性.研究结果可为该混沌系统的工程应用和电路设计提供一定的理论依据.

大气混沌模型；全局吸引性；有界性; 数值模拟

0 引 言

1963年,美国气象学家LORENZ[1]提出了大气热对流过程的动力学模型,即著名的Lorenz系统，并且发现了著名的蝴蝶效应.随后，众多学者对Lorenz系统的各种动力学行为展开了深入研究,揭示了Lorenz系统复杂动力学行为的演化过程及混沌的产生机制[2-14]，并将Lorenz系统应用于自然科学的各个领域.

著名学者STENFLO在研究大气的热对流运动时，给出了大气热对流运动的四维混沌模型[15-16]：

(1)

其中α,β,γ,c为系统(1)的正参数，变量w用于描述气流的旋转,参数γ(>0)是与w相对应的旋转数(rotation number),α(>0)表示普朗特数(Prandtl number),c(>0)表示瑞利数(Rayleigh number)，β(>0)为几何参数( geometric parameter).当c=26,β=0.7,γ=1.5,α=1时，系统(1)的混沌吸引子如图1所示，在平面yoz上的吸引子如图2所示.

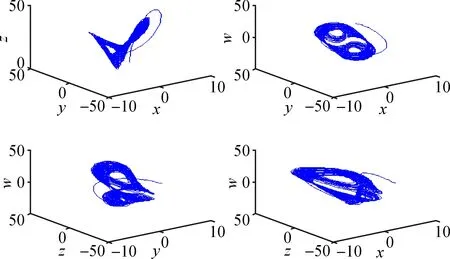
图1 系统(1)在3D空间中轨线的吸引子Fig.1 Chaotic attractor of system in 3D space

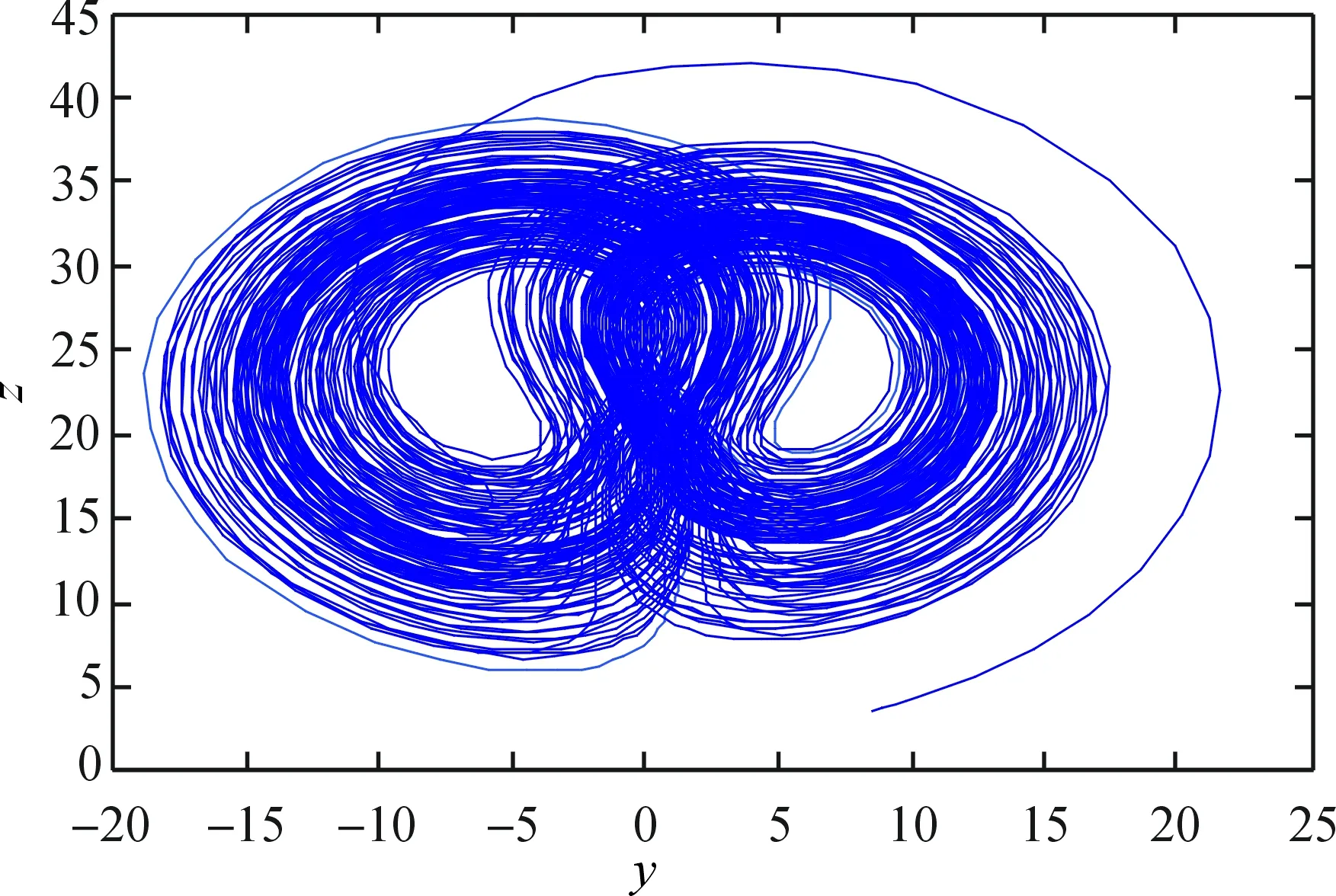
图2 系统(1)在yoz平面上轨线的吸引子Fig.2 Chaotic attractor of system in yoz plane

1 主要结果及证明

系统(1)的一些动力学行为： 模型的推导、混沌行为产生的机理等，文献[12]已有研究.下文主要研究系统(1)的最终界和全局吸引性.

引理1定义集合

令

则有

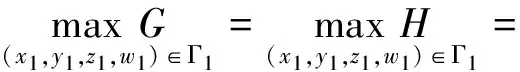
证明由多元函数求条件极值的拉格朗日乘数法即可证得.

引理2对任意的λ>0,m>0,α>0,β>0,γ>0,c>0,令

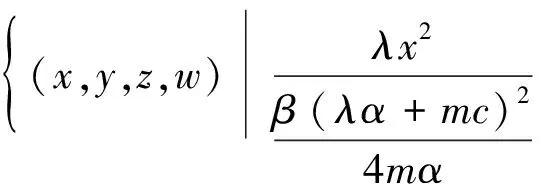
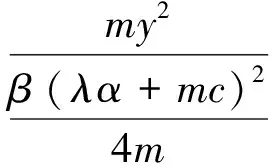
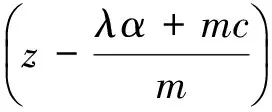
λγw2, ∀λ>0,m>0,

则有

证明令

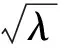
则有

V(x,y,z,w)=λx2+my2+

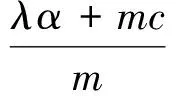
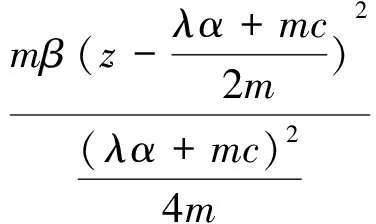
由引理1即可得到结论.

引理3定义

令

(z1-2c)2, (y1,z1)∈∑,

则有

证明由多元函数求条件极值的拉格朗日乘数法便可证得.

定理1对任意的λ>0,m>0,α>0,β>0,γ>0,c>0，

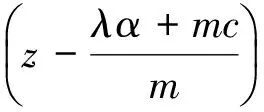
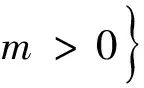
(2)

为系统(1)正半轨线的一个最终界和正向不变集.其中，

证明定义广义李雅普诺夫函数

V(x,y,z,w)=λx2+my2+

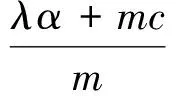
对上述函数求导有

2λx(αy-αx+γw)+2my(cx-xz-y)+

2λγw(-x-αw)=-2λαx2-2my2-

2mβz2+2β(λα+mc)z-2λγαw2,

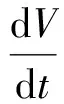
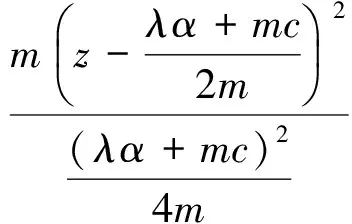
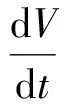
由引理2便可得到结论.

容易证明式(2) 为系统(1)正半轨线的一个最终界和正向不变集.

注1(i)令λ=1,m=1, 则

Ω1,1={(x,y,z,w)|x2+y2+(z-α-c)2+γw2≤l2}

是系统(1)正半轨线的一个最终界和不变集，其中，

当c=26,β=0.7,γ=1.5,α=1时，则有

Ω1,1在xoyz空间中的投影如图3所示.

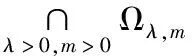
定理2令(x(t),y(t),z(t),w(t))为系统(1)的任意一个解.则对任意的α>0,β>0,γ>0,c>0，

Φ={(y,z)|y2+(z-c)2≤l2}

(3)

为系统(1)的y(t),z(t)的一个最终界.其中，

图3 系统(1)xoyz空间中的最终界估计图示Fig.3 Bounds of system (1) in xoyz space

证明定义广义李雅普诺夫函数

V1(y,z)=y2+(z-c)2,

则有

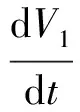
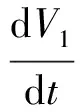
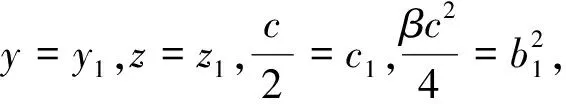
注2当c=26,β=0.7,γ=1.5,α=1时，有

Φ={(y,z)|y2+(z-26)2≤262}.

由Φ可以得到系统(1)正半轨线在yoz平面上的最终界估计，见图4.

由从吸引集外的轨线进入吸引集的速率估计，有

定理3令X(t)=(x(t),y(t),z(t),w(t))为系统(1)的任意一个解.则对任意α>0,β>0,γ>0,c>0,

Ω= {(x,y,z,w)|λx2+my2+

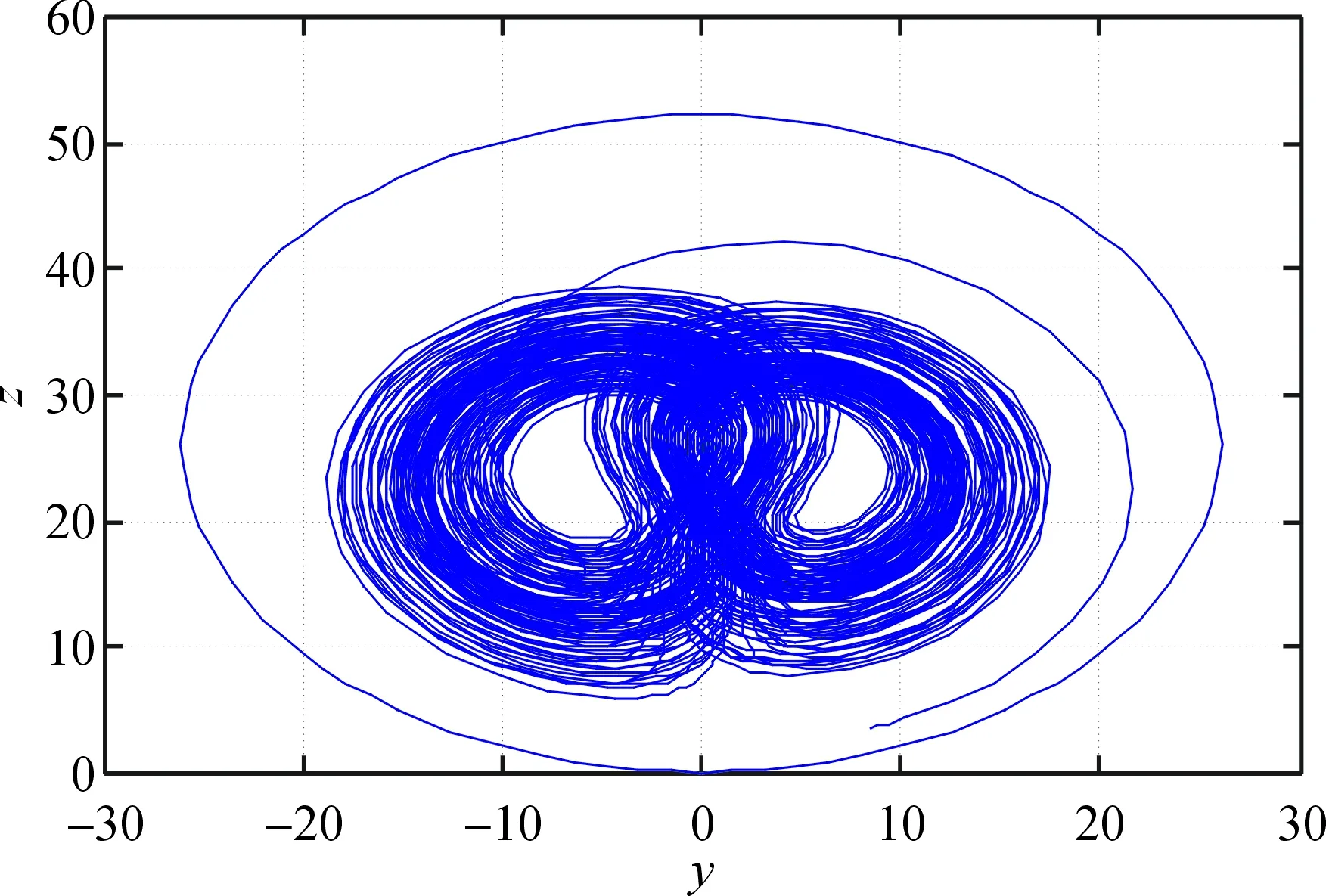
图4 系统(1)yoz平面上的最终界估计图示Fig.4 Bounds estimate of system (1) in yoz plane

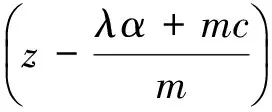
∀λ>0,∀m>0}

(4)

为系统(1)的一个全局指数吸引集.其中，

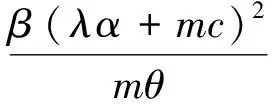
证明定义广义李雅普诺夫函数

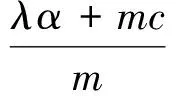
λγw2, ∀λ>0,m>0，

当V(X(t))>L,V(X(t0))>L时,有

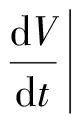
2λx(αy-αx+γw)+2my(cx-xz-y)+

-2λαx2-2my2-2mβz2+2β(λα+mc)z-

2λαγw2=-λαx2-my2-mβz2+

2β(λα+mc)z-γλαw2-λαx2-my2-mβz2-

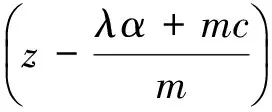
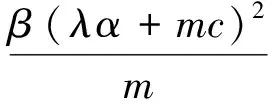
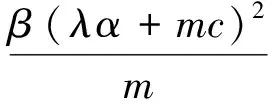
当V(X(t))>L,V(X(t0))>L时,有

V(X(t0))e-θ(t-t0)+L(1-e-θ(t-t0)),

从而有

[V(X(t))-L]≤[V(X0)-L]e-θ(t-t0).

令t→+, 对上述不等式两边取上极限，有

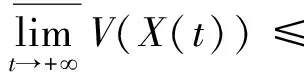
从而有

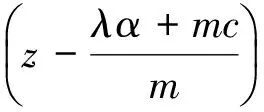
λγw2≤L,∀λ>0,∀m>0}

为系统(1)的一个全局指数吸引集.

证毕！

注3取λ=1,m=1, 则

Ω={(x,y,z,w)|x2+y2+(z-α-c)2+γw2≤δ}

为系统(1)的一个全局指数吸引集，其中，

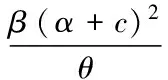
2 结 论

研究了一类大气混沌模型的全局吸引性和最终界.本研究方法亦适用于其他混沌系统；研究结果对于该混沌系统的混沌控制及其应用有一定的参考价值.

[1] LORENZ E N.Deterministic non periodic flow[J].JournaloftheAtmosphericSciences,1963,20(2)： 130-141.

[2] DOEDEL E J,KRAUSKOPF B,OSINGA H M.Global organization of phase space in the transition to chaos in the Lorenz system[J].Nonlinearity,2015,28(11)： 113-139.

[3] MESSIAS M.Dynamics at infinity and the existence of singularly degenerate heteroclinic cycles in the Lorenz system[J].JournalofPhysicsA(MathematicalandTheoretical),2009,42(11)： 115101.

[4] LEONID A B.Short and long-term forecast for chaotic and random systems (50 years after Lorenz’s paper) [J].Nonlinearity,2014,27： 51-60.

[5] SPARROW C.TheLorenzEquations：Bifurcations,Chaos,andStrangeAttractors[M].Netherlands： Springer Science & Business Media,2012： 20-30.

[6] STEWART I.The Lorenz attractor exists[J].Nature,2000,406： 948-949.

[7] TUCKER W.The Lorenz attractor exists[J].ComptesRendusdel’AcadémiedesSciences-SeriesI-Mathematics,1999,328(12)： 1197-1202.

[8] POGROMSKY A Y,SANTOBONI G,NIJMEIJER H.An ultimate bound on the trajectories of the Lorenz systems and its applications[J].Nonlinearity,2003,16： 1597-1605.

[9] LLIBRE J,ZHANG X.Invariant algebraic surfaces of the Lorenz system[J].JournalofMathematicalPhysics,2002,43： 1622-1645.

[10] KRISHCHENKO A P,STARKOV K E.Localization of compact invariant sets of the Lorenz system[J].PhysicsLettersA,2006,353： 383-388.

[11] ZHANG F C,ZHANG G Y.Further results on ultimate bound on the trajectories of the Lorenz system[J].QualitativeTheoryofDynamicalSystems,2016,15(1)： 221-235.

[12] ZHANG F C,LIAO X F,ZHANG G Y,et al.Dynamical analysis of the generalized Lorenz systems[J].JournalofDynamicalandControlSystems,2017,23(2)： 349-362.

[13] ZHANG F C,LIAO X F,ZHANG G Y.Qualitative behavior of the Lorenz-Like chaotic system describing the flow between two concentric rotating spheres[J].Complexity,2016,21(S2)： 67-72.

[14] ZHANG F C,MU C L,ZHOU S M, et al. New results of the ultimate bound on the trajectories of the family of the Lorenz systems[J].DiscreteandContinuousDynamicalSystems：SerB,2015,20(4)： 1261-1276.

[15] LORENZ S.Generalized Lorenz equations for acoustic-gravity waves in the atmosphere[J].PhysicaScripta,1996,53(1)： 83-84.

[16] 韩修静,江波,毕勤胜.快慢Lorenz-Stenflo 系统分析[J].物理学报,2009,58(7)： 4408-4414.

HAN X J,JIANG B，BI Q S.Analysis of the fast-slow Lorenz-Stenflo system[J].ActaPhysicaSinica,2009,58(7)： 4408-4414.

ZHANG Yong1,YANG Xueling2,SHU Yonglu3
(1.BasicTeachingDepartmentofHenanPolytechnicInstitute，Nanyang473000,HenanProvince,China; 2.DepartmentofAutomobileEngineering,HenanPolytechnicInstitute,Nanyang473000,HenanProvince,China; 3.CollegeofMathematicsandStatistics,ChongqingUniversity,Chongqing401331,China)

Based on the existed literature, this paper studies the domains of attraction of the atmospheric chaos model by theoretical analysis of the dynamical systems and computer simulation. The analytical expressions of the domains of attraction of the atmospheric chaos model are derived. Numerical simulations confirm the theoretical analysis results. The results have good reference value for the stable operation of this kind of system, and provide theory basis for the application in engineering and circuit design of this system.

atmospheric chaotic model; global attractability; the boundedness; numerical simulation

2016-10-04.

国家自然科学基金资助项目(11171360).

张勇(1981—)，ORCID： http： //orcid.org/0000-0001-6973-4529，男，硕士，副教授，主要从事混沌系统理论及其应用研究，E-mail： zhangyongzhang2013@163.com.

10.3785/j.issn.1008-9497.2018.01.004

O 241.84

A

1008-9497(2018)01-018-05

Dynamicalbehaviorsofanewatmosphericchaosmodelanditsnumericalsimulation.Journal of Zhejiang University(Science Edition),2018,45(1)： 018-022