秘鲁Mw≥6.9地震趋势判断与时空对称规律

王辉，延军平*，唐宝琪，李英杰(. 陕西师范大学 地理科学与旅游学院， 陕西 西安 709； 2. 地理学国家级实验教学示范中心(陕西师范大学)， 陕西 西安 709)

秘鲁Mw≥6.9地震趋势判断与时空对称规律

王辉1,2，延军平1,2*，唐宝琪1，李英杰1
(1. 陕西师范大学 地理科学与旅游学院， 陕西 西安 710119； 2. 地理学国家级实验教学示范中心(陕西师范大学)， 陕西 西安 710119)

选取秘鲁地区1970年以来Mw≥6.9的地震数据，根据可公度性理论，提取秘鲁强震的可公度信息，采用蝴蝶结构图、可公度网络结构图和震中迁移方法，探索该地区强震活动的时空对称性，同时对可能触发地震的天文现象与地震灾害的发生进行相关分析，进一步验证趋势判断结果，发现相关规律. 研究结果表明： 1970年以来秘鲁Mw≥6.9地震具有可公度性，2019年在秘鲁北部(73°W，11°S附近)发生中深源地震的信号较强；太阳活动、地球自转、月球运动与秘鲁地震的发生具有一定相关性，秘鲁Mw≥6.9地震发生在太阳活动峰值年、下降段的占77.78%，发生在太阳活动双周期的占66.67%，发生在地球自转变化率较大年份的占60%，朔月前后是地震频发期(占44.44%)，朔月、下弦月前后地震发生次数达83.33%.

可公度；时空对称；趋势判断；太阳黑子；地震

在全球变化的背景下，重大自然灾害频繁发生，适应并应对灾害发生是当前人类社会亟须解决的重要问题[1]. 地震可在短时间内造成重大损害. 且当前人类对其认识与适应能力仍较为薄弱，这对人类的生命、生产和生活造成了极大的威胁. 通过物理建模揭示地震发生的内部机制并做出准确的预测是地震学家需要解决的一个重大难题，但至今仍未实现. 数学预测是一种不同于物理方法且较为有效的地震预测方法，可以协助或弥补部分目前物理预测方法中存在的缺陷，因此，借鉴理论物理学的科学研究路径，利用对称性原理，承认表象模式，以揭示地震内在的发生机理[2]. 任何事物或现象的发生都是在一定的时间和空间内的，许绍燮[3]认为“强震发生不是随机的，但并不是什么地方都会发生，强震在空间上具有一定的有序性”. 延军平等[4]认为： “并非所有的灾害都是对称的，但其中有些是比较对称的；并不是所有区域的灾害都是对称的，但一些地区的灾害更为对称；并非所有时期的灾害都是对称的，但某些时期的灾害可能更为对称”.

20世纪80年代，翁文波[5]提出了信息预测论，并将其应用于自然灾害预测[6-7]. 此后，国内学者在此基础上对地震[8-12]、旱涝[13-15]、雪灾[16]、热带气旋[17]、火山[18]等自然灾害进行了趋势判断并探索其相关规律，逐步形成一套较为完善的方法体系[2，19-20]. 现有研究表明，部分强震具有可公度性和时空对称性特征，但不同地区地震的物理机理、时空规律存在一定差异. 目前，对地震时空对称性特征的探索已较为成熟，而对相关机理及规律的探索相对薄弱. 因此，对典型区域的地震灾害趋势判断与时空规律探索，有助于提高灾害预测预报水平和防灾减灾能力.

秘鲁位于环太平洋地震带东环，是一个地震多发的国家，地震灾害多分布在沿海人口密集地区. 从板块构造上看，秘鲁处于南美洲板块与纳斯卡板块之间，纳斯卡板块向东俯冲于南美洲板块和安第斯山脉下，形成“秘鲁-智利”海沟. 秘鲁所处的地质环境较为复杂、特殊，地震频发，其可公度性、时空对称性是否显著？与哪些致灾因子相关？相关程度如何？这些问题下文将逐一予以探讨.

首先，运用可公度理论判断秘鲁地震的可公度性，并提取相应信息；其次，利用时空对称性方法研究秘鲁地震的时空变化趋势，对未来可能发生地震的时间、空间进行预测；最后，分析太阳黑子活动、地球运动和月球运动等可能的致灾因子与秘鲁地震的相关关系，探索秘鲁地震发生的时空规律.

1 研究区与数据来源

1.1 研究区概况

秘鲁地处南美洲西部、太平洋东岸(见图1)，安第斯山脉贯穿秘鲁南北，西部沿海地区是干旱平原地带，东部为亚马逊盆地的热带雨林区，秘鲁矿产资源、渔业资源、旅游资源丰富. 地震灾害对秘鲁的社会经济发展威胁巨大，2012—2017年短短5a间已发生4次Mw≥6.9地震，而2001年6月23日在南部发生的8.4级地震，不仅造成了严重的人员伤亡和财产损失，还导致许多古文化遗址被摧毁.

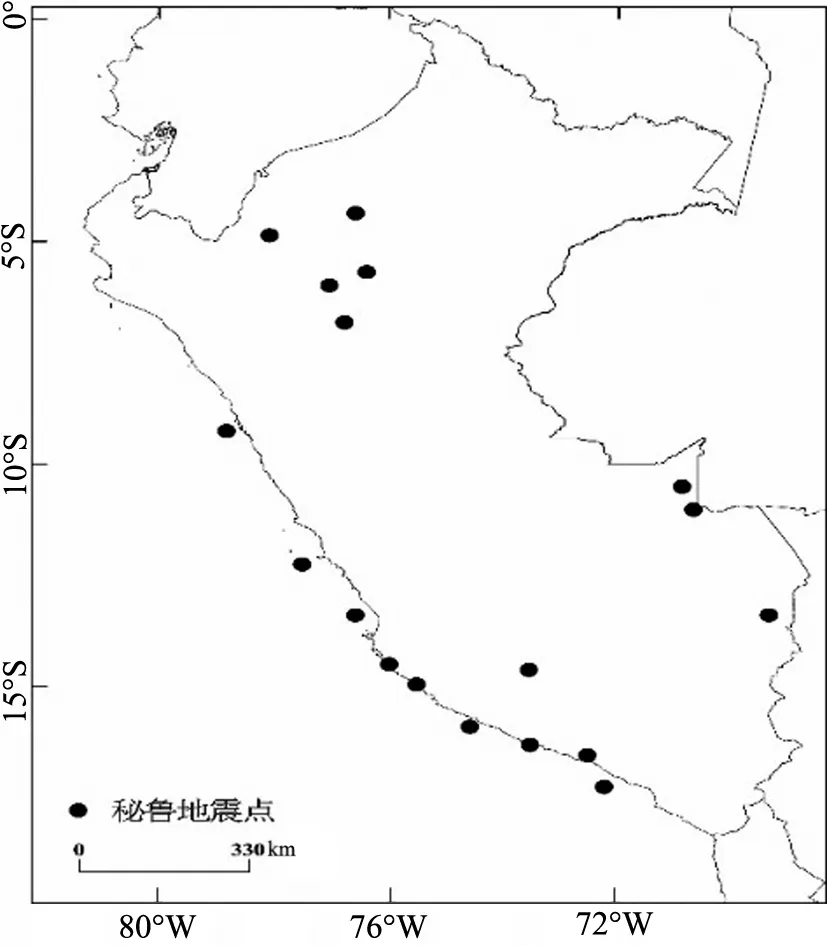
图1 研究区示意图Fig.1 Schematic location of study area

1.2 数据来源

全文数据包括地震信息数据、太阳黑子相对数、地球自转数据. 其中，地震数据资料主要来源于《全球地震目录》[21]和中国地震信息网，通过对秘鲁地震可公度性的检验，提取了1970—2015年秘鲁Mw≥6.9地震数据资料(见表1)；太阳活动的黑子相对数数据来自美国国家地球物理数据中心；地球自转(日长)数据来自国际地球自转服务组织(International Earth Rotation Service IERS, http： //hpiers.obspm.fr/).

1.3 研究方法

1984年翁文波[22]创造性地提出可划分为3个层次的认识体系，即抽象体系、物理体系、信息体系，并创立了信息预测理论. “可公度是自然界的一种秩序，是一种信息系”.相关可公度性理论方法可参见文献[5，20，22]. 三元可公度计算方法为：Xk=Xh+Xi-Xj，其中k=h+i-j[23]；h，i，j∈[1,18]，k为要判断的第k个强震可能发生的年份，如要判断第19个地震，则k=19.

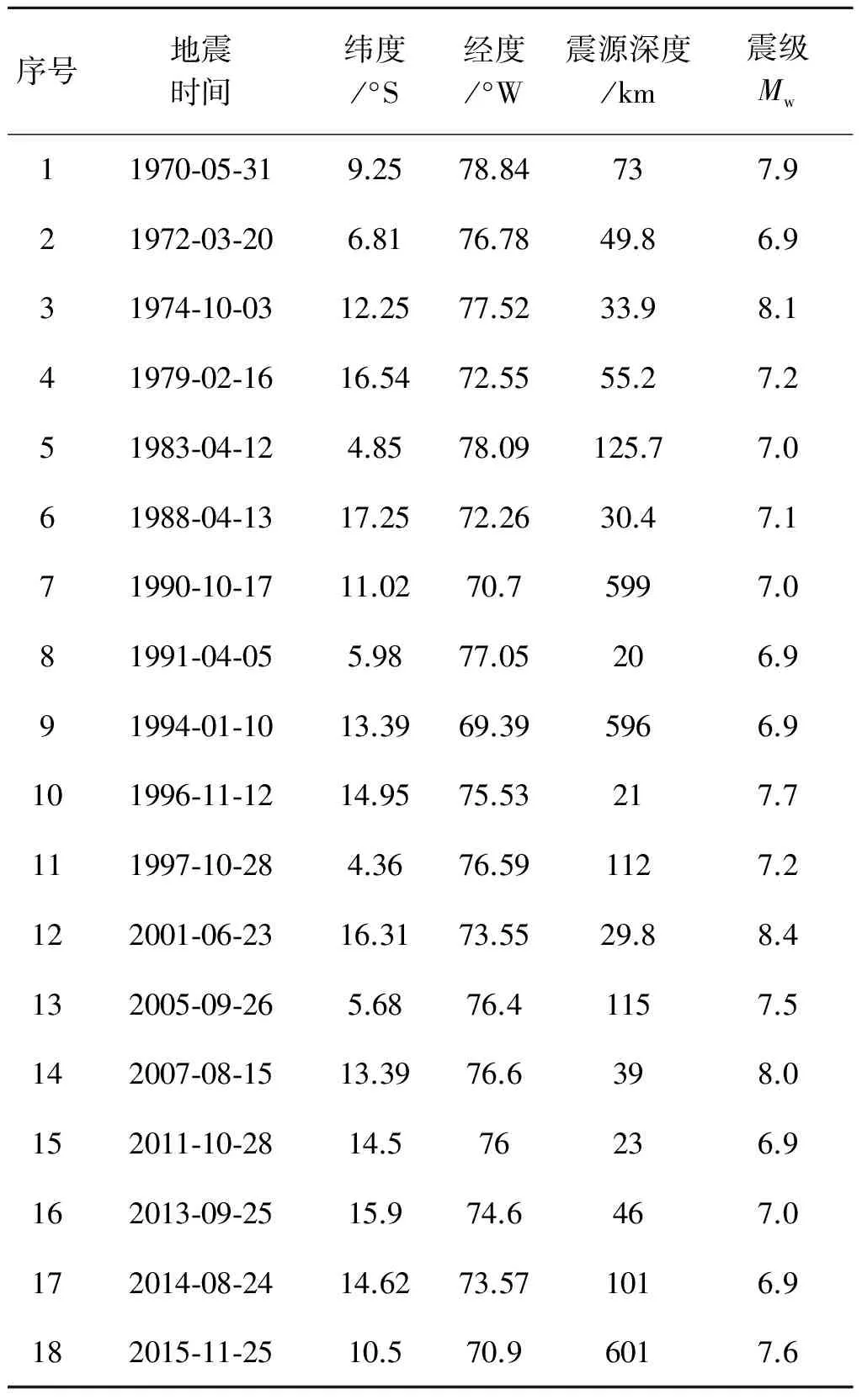
表1 秘鲁1970—2015年Mw≥6.9地震信息统计表Table 1 Catalogue of Mw≥6.9 earthquakes in Peru from 1970 to 2015

四元可公度计算该周期： ΔX=Xh+Xi-Xj-Xk，其中h+i=j+k，判断下一次自然灾害发生年份Xn，Xn=Xm+ΔX，Xm为地震最近一次发生的年份，即X19=X18+ΔX[23].

五元可公度间隔外推式：Xn=Xh+Xi+Xj-Xk-Xl，其中n=h+i+j-k-l[23].

随机性概率计算方法为：P=M/N，不漏报置信水平为(1-α)=M/(N+1)，其中，P为灾害事件时间序列中预测年份发生的可能概率，N为灾害事件次数总和，M为参与实际预测的灾害次数，即和主周期关联的年份统计[23].

在可公度性方法的基础上，延军平等[2，4]从对灾害趋势判断的研究转向灾害对称性结构分析. 综合已有研究方法，本文在信息预测理论的基础上提取秘鲁强震信息，判断秘鲁强震的可公度性，并验证三元可公度性，继而利用时空对称性结构分析方法研究秘鲁强震的时空变化特征，旨在探求灾害发生的时空规律(见图2). 其中，蝴蝶结构图和可公度结构系被用来探讨地震的时间对称性和趋势性；震中空间迁移用以探索强震空间对称性. 最后，通过分析秘鲁强震发生信息与相关影响因素之间的相关性，总结了秘鲁强震与相关因素的变化规律.

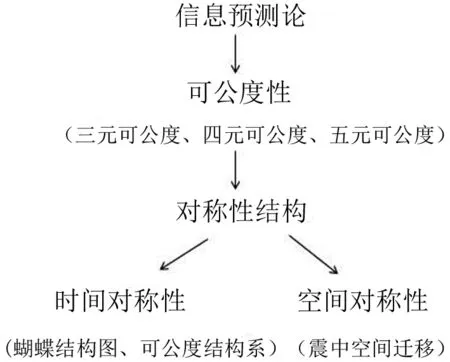
图2 研究方法Fig.2 The study method

2 时间对称性及趋势判断

2.1 可公度趋势判断

2.1.1 三元可公度趋势判断

1970年以来，秘鲁地区Mw≥6.9地震发生了22次，其中1970年、1996年、1997年、2001年均发生了2次以上Mw≥6.9地震，强震群以其主震为代表，统一年份强震以最大一次为代表[10]，对秘鲁地区18次地震的可公度性进行分析.

设X1=1970；X2=1972；X3=1974；X4=1979；X5=1983；X6=1988；X7=1990；X8=1991；X9=1994；X10=1996；X11=1997；X12=2001；X13=2005；X14=2007；X15=2011；X16=2013；X17=2014；X18=2015；X19=？

根据三元可公度式计算，结果为： 2016年5组；2017年9组；2018年6组；2019年13组；2020年10组；2021年8组；2022年10组；2023年7组. 其中，2019年信号最强.

为了验证可公度趋势判断的有效性，通过历史强震进行三元可公度验证计算(见表2)，结果表明秘鲁地区历史强震具有良好的可公度性，至少可得到12组以上的可公度式子.

2.1.2 四元、五元可公度趋势判断

通过四元、五元可公度计算方法，分别得到以下结果：

表2 三元可公度式验证表Table 2 The confirmation of earthquakes base on commensurable method

四元可公度计算结果为： 2016年99次；2017年88次；2018年83次；2019年52次；2020年33次.

五元可公度计算结果为： 2016年532次；2017年653次；2018年721次；2019年800次；2020年850次.

可公度法计算主要以三元可公度为主，四元、五元可公度为参考，后者对趋势判断结果的验证具有修正和借鉴作用. 综合判断，2019年发生Mw≥6.9地震的信号较强.

2.2 蝴蝶结构图趋势判断

根据可公度信息，绘制蝴蝶结构图(见图3)，发现秘鲁Mw≥6.9地震的时间对称性较强. 与2019年相关的周期有8组，分别是4，5，6，8，14，18，22和23 a. 对秘鲁Mw≥6.9地震发生的趋势判断进行检验，其随机性概率P为55.56%，不漏报置信水平(1-α)为52.63%. 因此，2019年发生地震的可能性较大.

图3 秘鲁Mw≥6.9地震序列蝴蝶结构图Fig.3 The butterfly structure of Mw≥6.9 earthquakes in Peru

2.3 可公度结构系趋势判断

根据秘鲁Mw≥6.9地震的蝴蝶结构图时间对称特点，绘制1970年以来秘鲁Mw≥6.9地震的可公度结构系(见图4)，其结构系完整，网络特征明显. 横向呈现9,17 a的主周期和11,10,8 a的次周期；纵向呈现4 a的主周期和14，2，17 a的次周期. 根据平移对称性推断，2019年将可能发生地震.

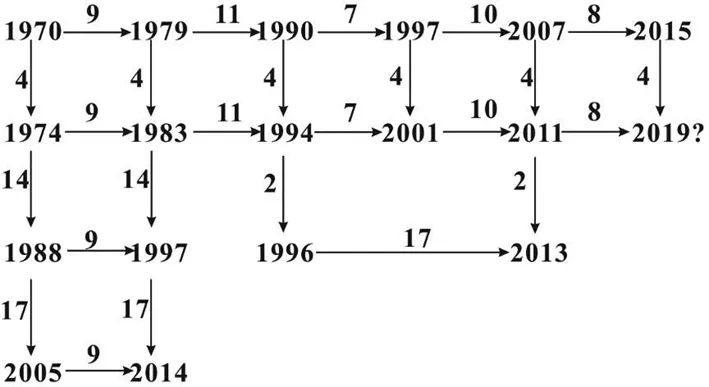
图4 秘鲁Mw≥6.9地震可公度结构系图Fig.4 Ordered network structure of Mw≥6.9 earthquakes in Peru

3 空间对称性及趋势判断

3.1 地震震中空间分布特征

1970—2015年，秘鲁Mw≥6.9地震震中的空间分布集中于西南部沿海、北部和东部平原区，基本可划分为2个区域： 沿海地震带和内陆平原地震带. 沿海地震带以浅源地震为主，破坏性强、影响程度大，沿海也是秘鲁人口、经济、文化、城市集中分布的地区；平原地震带处于亚马孙河流域，以中源、深源地震为主，强震发生时间间隔较长，影响较小.

3.2 地震震中的经向、纬向迁移

地震迁移是指破坏性地震沿一定空间有规律地相继发生的现象，当不涉及地震沿深度方向迁移时，称为“震中迁移”[24]. 目前，运用震中迁移研究地震的空间变化已较丰富，震中迁移带交汇区可能对大震位置的预测有一定价值[25].

从经纬向迁移关系看，秘鲁地震震中在经纬向迁移变化中具有复杂多变性，经纬向迁移并非一致同步的，而是“同向-反向-同向”交替出现(见图5). 经向呈“东-西-东-西”变动规律，纬向呈“北-南-北-南”变动规律，单向上具有一定空间对称性.

据此判断，下一次秘鲁Mw≥6.9地震可能会发生在西经73°以东、南纬11°以北地区，大体位于秘鲁东北洛雷托区，且中源或深源地震的可能性较大.

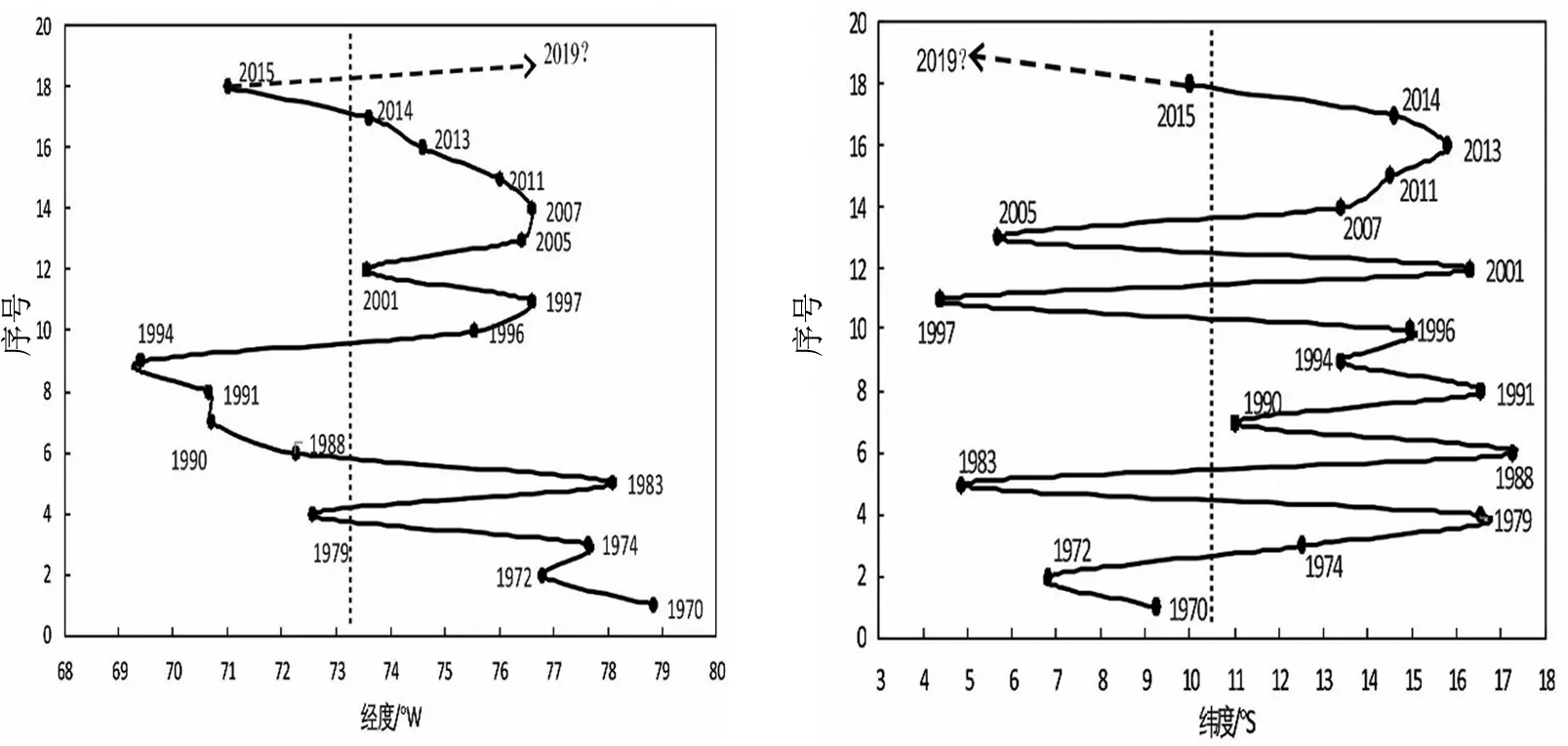
图5 秘鲁Mw≥6.9地震震中迁移Fig.5 The migration trend of Mw≥6.9 earthquake in Peru

4 秘鲁地震相关机理分析

4.1 太阳黑子活动与秘鲁地震相关性分析

太阳活动与地震的相关机理表现为： 当太阳活动加强或减弱时，其向外发射的电磁粒子量也会随之变化，异常的电子流穿过地球的岩石晶体时会促使岩石内部部分分子键崩解，降低地表岩石强度，从而诱发地震[26-29].

1970年以来秘鲁Mw≥6.9地震与太阳黑子活动在统计学上存在明显的相关关系，主要表现在太阳黑子活动的阶段和周期上： (1) 发生在太阳黑子活动峰值年附近和下降段的地震次数各占38.89%，总计约78%；地震发生在太阳黑子活动的上升段和谷值年附近较少，各占11.11%(见表3). (2) 从太阳黑子活动周期数看，秘鲁地震大多发生于双周期，占总发震次数的66.67%(见表4)，2009年以来太阳黑子正处于第24周期. 根据太阳黑子活动11 a周期的规律，秘鲁未来发生强震信号最强的年份2019年正处于太阳黑子数下降段和双周期内(见图6)，这进一步增强了趋势判断的可信度与合理性.

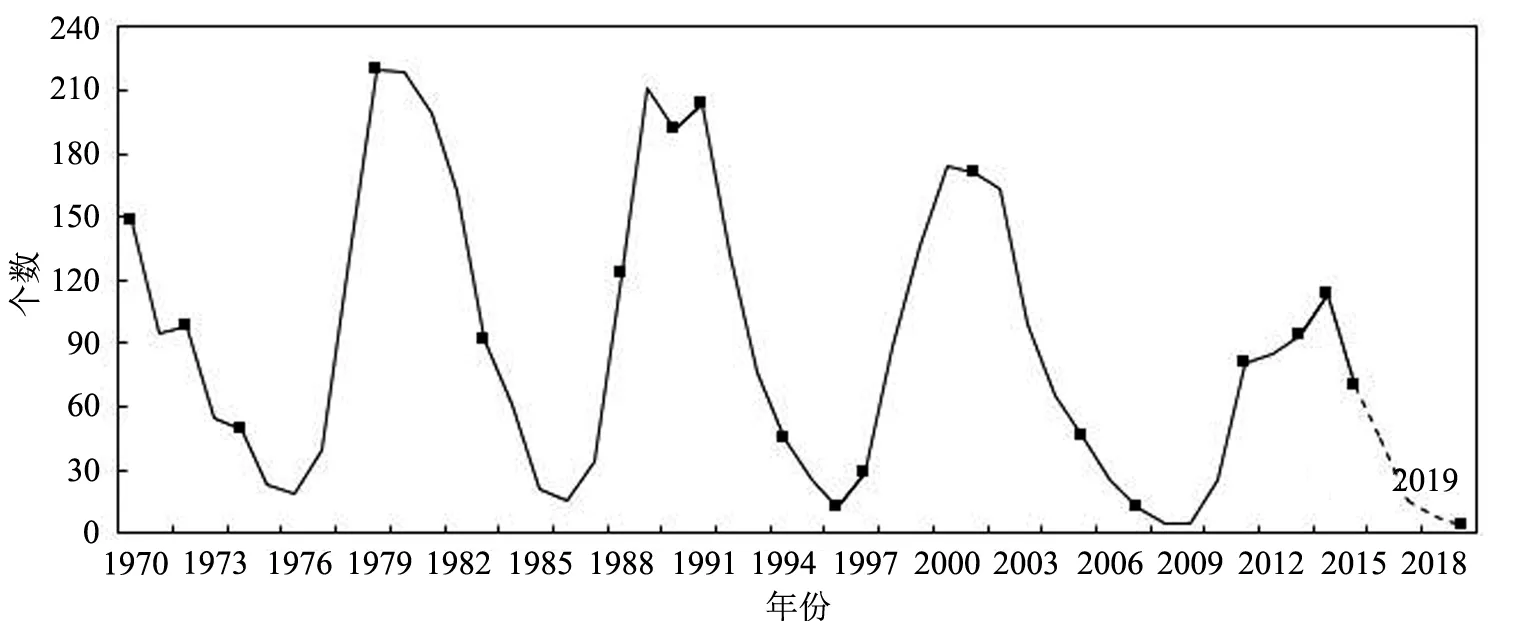
图6 秘鲁Mw≥6.9地震与太阳黑子数的相关性分析Fig.6 The correspondence between Mw≥6.9 earthquakes and Sunspot number in Peru

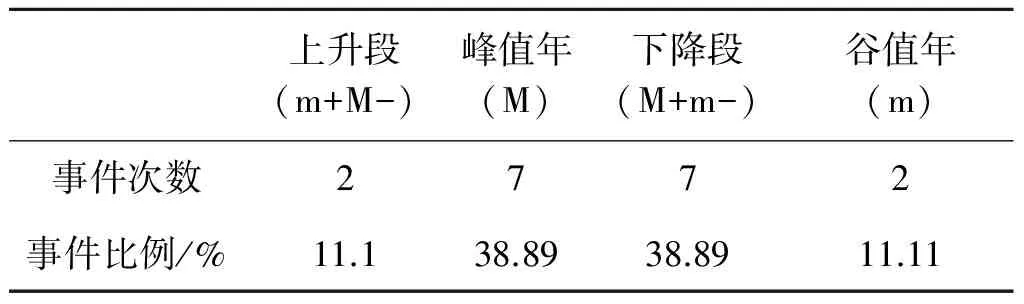
表3 太阳活动的不同阶段强震事件发生的次数及比例Table 3 The frequency of earthquake events in different stages of solar activity

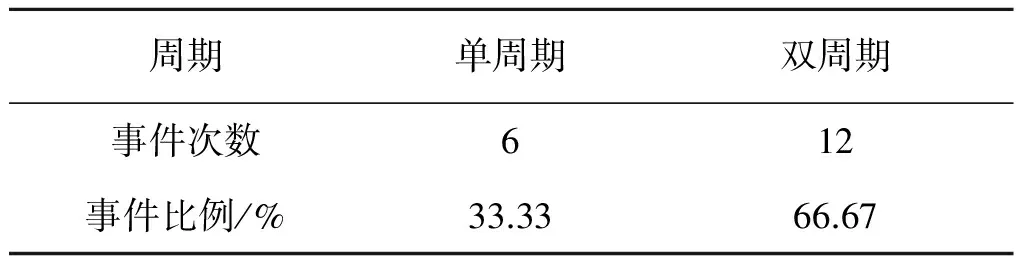
表4 太阳活动周期中强震事件发生的次数及比例Table 4 The frequency of earthquake events in different cycles of solar activity

4.2 地球自转与秘鲁地震相关性分析

地球自转与全球强震的发生在统计学上具有相关性，只是不同地区存在差异，有的地区与地球自转减速有关，而有的地区则与地球自转加速有关[30]. 地球自转速率变化可能是全球地震活动的主要动力来源[31].

通过对比秘鲁1970年以来6.9级以上地震与地球日长变化趋势，可以发现秘鲁地震与地球自转速度的关系(见图7). 秘鲁地震发生在地球自转速度减速期和加速期的比例为 12∶6，加速期年均发生地震0.29次，减速期年均发生0.5次，减速期发生地震的可能性高于加速期. 强震发生在地球自转速度变化率较大的年份(1988—1997年、2011—2015年)，占发震年份的60%，这与相关研究结论较为一致[29]. 自2013年以来，地球自转速度出现大幅的变速期，2019年仍可能处于这一时期，因此，对2019年秘鲁发生强震的趋势判断可信度较高.

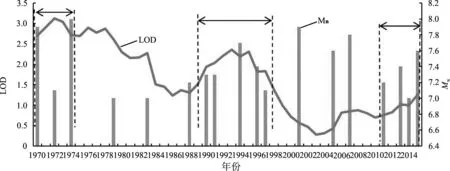
图7 秘鲁Mw≥6.9地震与地球自转日长的关系Fig.7 The relationship between Mw≥6.9 earthquakes in Peru and the earth rotation

4.3 月相变化与秘鲁地震的相关性分析

相关研究表明，月球运动对某些地区的地震活动有明显影响[32]，其原因可能与固体潮有关. 朔望时的潮汐力最大，而朔时的起潮力又比望时大，海洋潮汐最大日一般发生在初二和十七[33].

1970年以来，秘鲁Mw≥6.9地震事件中，发生在朔前后的有8次，占44.44%，其次是下弦前后，两者合计占83.33%(远高于50%)，18次地震中望月前后仅发生2次，且相隔时间较长，说明秘鲁的大地震与朔、下弦的关系密切(见表5和6). 最近一次地震发生在望前后，据此判断下一次地震发生在下弦、朔前后，即农历廿十至初五.

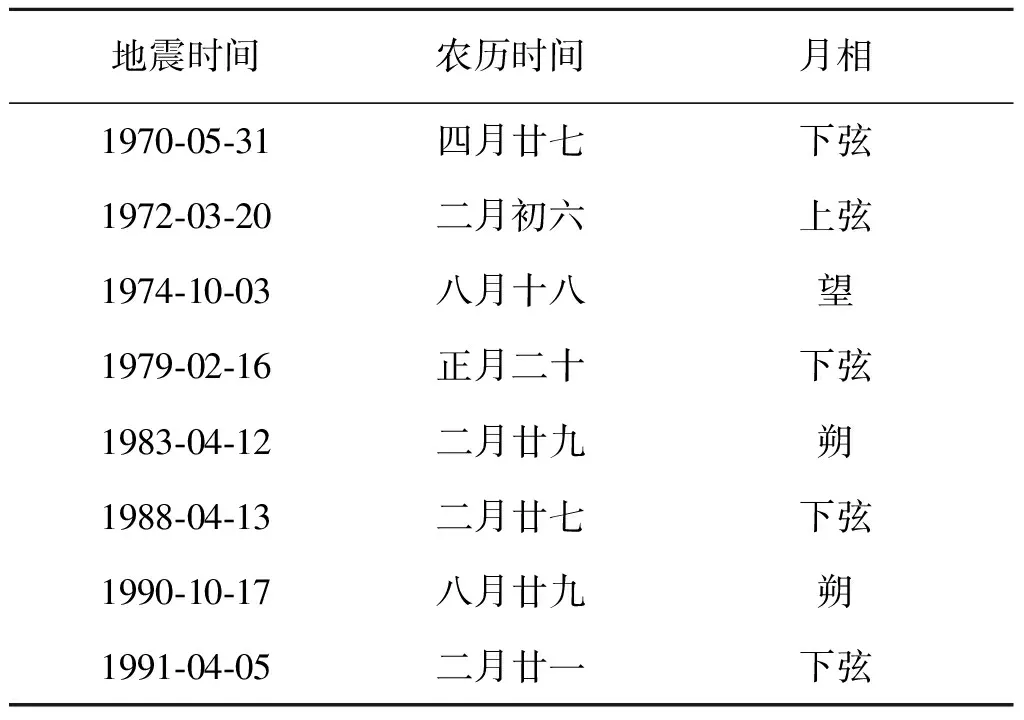
表5 秘鲁Mw≥6.9地震与月相关系Table 5 The relationship between Mw≥6.9 earthquake events and Lunar movement

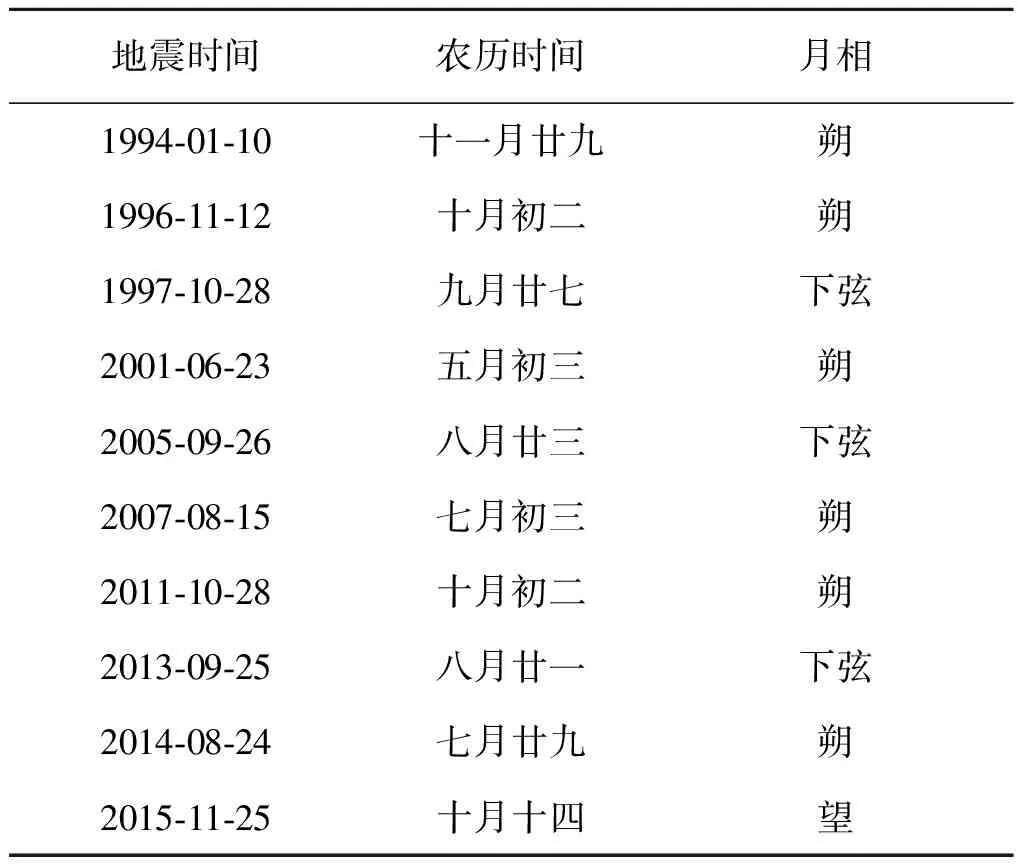
续表5

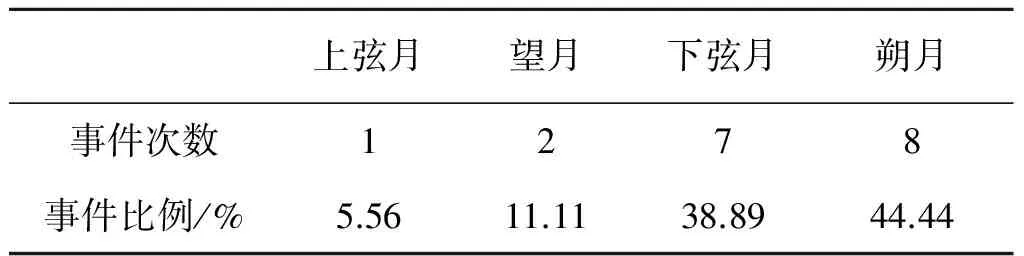
表6 不同月相变化时期的强震事件发生次数及比例Table 6 The frequency of earthquake events in different cycles of Lunar movement

5 结论与讨论

通过对秘鲁1970年以来Mw≥6.9地震时空对称性规律的探索，从地理学视角研究历史时期地震时空对称性与物理力源的可能叠加结果，进而探讨了对秘鲁地震发生的相关机理，得到以下结论：

5.11970年以来，秘鲁Mw≥6.9地震发生时间具有良好的可公度性，结合三元、四元、五元可公度计算，2019年秘鲁发生Mw≥6.9地震信号较强.

5.22019年秘鲁发生Mw≥6.9地震的随机性概率达60%，不漏报置信水平(1-α)为52.63%，可公度法与蝴蝶结构图法得到的结果显示出高度的一致性.

5.3近65a来，秘鲁Mw≥6.9地震的震中迁移复杂多变，单向上具有一定的时间对称性. 未来强震震中可能向西北方向迁移，即在73°W以西，11°S以北地区.

5.4秘鲁Mw≥6.9强震与地球自转速度、太阳黑子、月球运动在统计学上具有良好的相关关系. 地震主要发生在地球自转的减速期，而且往往发生在地球自转速率相差较大的年份；此外，地震多发生在太阳黑子双周期、下降段和峰年附近；下弦、朔月前后是地震的多发时期. 秘鲁强震与主要天文运动的高度相关性规律对于区域灾害防治具有重要意义.

运用时空对称性方法判断地震灾害趋势方法体系比较成熟，也具一定的准确性. 其局限性可能在趋势判断的精确度和地震灾害的内在机理与形成机制等方面.因此，案例研究的扩展和方法体系的构建以及跨学科交叉协作将是下一步研究的重点.

[1] 延军平.重大自然灾害时空对称性研究[M].西安： 陕西师范大学出版总社有限公司,2013.

YAN J P.StudyonSpatiotemporalSymmetryofNaturalDisasters[M]. Xi’an： Shaanxi Normal University Publishing House Limited，2013.

[2] 延军平，闫娜.关于地震预测体系构建的可能性及验证[J].陕西师范大学学报(哲学社会科学版)，2008，37(5)： 19-23

YAN J P, YAN N.Probability and verification of constructing an earthquake predicting system [J].JournalofShaanxiNormalUniversity(PhilosophyandSocialSciencesEdition)，2008, 37(5)： 19-23.

[3] 许绍燮.地震应可预测[M].北京： 地震出版社，2011.

XU S X.TheEarthquakePrediction[M]. Beijing： Seismological Press，2011.

[4] 延军平，李双双，刘新颜，等.基于对称性的中国台湾地震趋势判断及物理基础[J].灾害学，2013,28(1)： 11-14,27.

YAN J P, LI S S, LIU X Y, et al. The trend judgment of earthquake in Taiwan based on symmetry theory and its physical basis [J].JournalofCatastrophology，2013,28(1)： 11-14,27.

[5] 翁文波.预测论基础[M].北京： 石油工业出版社,1984.

WENG W B.FundamentalsofForecastingTheory[M]. Beijing： Petroleum Industry Press，1984.

[6] 翁文波，吕牛顿，张清.预测学[M].北京： 石油工业出版社，1996

WENG W B, LYU N D, ZHANG Q.TheoryofForecasting[M]. Beijing： Petroleum Industry Press，1996.

[7] 翁文波，张清.天干地支纪历与预测[M]. 北京： 石油工业出版社，1993

WENG W B, ZHANG Q.TheGan-ZhiCalendarSystemandForecasting[M]. Beijing： Petroleum Industry Press，1993.

[8] 龙小霞,延军平,孙虎,等.基于可公度方法的川滇地区地震趋势研究[J].灾害学,2006,21(3)： 81-84.

LONG X X, YAN J P, SUN H, et al. Study on earthquake tendency in Sichuan-Yunnan region based on commensurability [J].JournalofCatastrophology，2006, 21(3)： 81-84.

[9] 门可佩.青藏高原北部地区7级强震的有序网络特征及其预测研究[J].地球物理学进展，2003,18(3)： 765-771.

MEN K P. Ordered network feature ofM≥7 earthquakes and its prediction in northern part of Qinghai-Xizang Plateau [J].ProgressinGeophysics，2003,18(3)： 765-771.

[10] 李双双，延军平.西太平洋俯冲带北部地区Ms≥8强震时空对称特征[J].地球物理学进展，2012,27(3)： 960-966.

LI S S, YAN J P. Space-time symmetry ofMs≥8 earthquake in North-Western Pacific Plate subduction [J].ProgressinGeophysics， 2012,27(3)： 960-966.

[11] MEN K P，ZHAO K. The 2015 NepalM8.1 earthquake and the prediction forM≥8 earthquakes in West China [J].NaturalHazards, 2016,82(3)： 1767-1776.

[12] 丁彩霞，延军平，林敏敏，等. 意大利Ms≥6地震时空对称性趋势判断[J].干旱区资源与环境，2014,28(8)： 50-54.

DING C X, YAN J P, LIN M M,et al. Research on space-time symmetry ofMs≥6 earthquake disasters in Italy [J].JournalofAridLandResourcesandEnvironment，2014,28(8)： 50-54.

[13] MEN K P. On the characteristics of the ordered network structure for severe floods and droughts over China with the application to prediction [J].ProgressinGeographysics,2005,20(3)： 867-876.

[14] 李梦洁，延军平.河南省旱灾对称性特征及趋势判断[J].干旱区资源与环境，2012,27(8)： 71-75

LI M J, YAN J P. Symmetry characteristics and trend judgment of drought in Henan [J].JournalofAridLandResourcesandEnvironment，2012,27(8)： 71-75.

[15] 吴梦初，延军平，刘栎彬.甘肃省雨涝灾害时间对称性及趋势判断[J].干旱区资源与环境，2014,28(8)： 125-131.

WU M C, YAN J P, LIU L S. Water logging disasters tendency judgment in Gansu province based on commensurability [J].JournalofAridLandResourcesandEnvironment，2014,28(8)： 125-131.

[16] 张涛涛.气候变化下青藏高原雪灾趋势判断及相关机理分析[D].西安： 陕西师范大学，2013.

ZHANG T T.TheTrendJudgmentandRelatedMechanismofQinghai-XizangPlateau[D]. Xi’an： Shaanxi Normal University，2013.

[17] 刘永林，延军平.香港热带气旋趋势判断及相关机理分析[J].地球物理学进展，2015，30(1)： 15-21.

LIU Y L, YAN J P. The trend judgment and related mechanism of Hong Kong tropical cyclones [J].ProgressinGeophysics,2015,30(1)： 15-21.

[18] 芦佳玉，延军平.印度尼西亚VEI≥4的火山喷发活动规律及未来趋势统计研究[J].地球物理学进展，2016,31(5)： 1953-1958.

LU J Y, YAN J P. Active pattern and future trend of volcanic eruption with VEI≥4 in Indonesia region [J].ProgressinGeophysics，2016,31(5)： 1953-1958.

[19] 延军平，白晶，苏坤慧，等.对称性与部分重大自然灾害趋势研究[J].地理研究，2011,30(7)： 1159-1168.

YAN J P, BAI J, SU K H, et al. Research on symmetry and theory of several major natural disasters [J].GeographicalResearch，2011,30(7)： 1159-1168.

[20] 延军平，李英杰，李双双，等.重大自然灾害时空对称性方法体系综述[J].灾害学，2017,32(1)： 149-154,182.

YAN J P, LI Y J, LI S S,et al. Review on spatiotemporal symmetry methodology of natural disasters [J].JournalofCatastrophology,2017,32(1)： 149-154,182.

[21] 宋治平,张国民,刘杰,等.全球地震目录[M].北京： 地震出版社,2011.

SONG Z P, ZHANG G M, LIU J, et al.GlobalEarthquakeCatalog[M]. Beijing： Seismological Press，2011.

[22] 翁文波.可公度性[J].地球物理学报,1981,24(2)： 151-154.

WENG W B. Commensurability[J].ActaGeophysicaSinica，1981，24(2)： 151-154.

[23] 李双双.对称性与部分强震时空结构及其物理机制分析[D]. 西安： 陕西师范大学，2013

LI S S.ResearchonSymmetryandSpace-TimeStructureandItsMechanismofSeveralStrongEarthquake[D]. Xi’an： Shaanxi Normal University，2013.

[24] 郭增建,秦保燕.地震迁移问题(综述)[J].国际地震动态,1983(1)： 7-10.

GUO Z J, QIN B Y. Problems of earthquake migration(an overview)[J].RecentDevelopmentinWorldSeismology,1983(1)： 7-10.

[25] 郭增建，郭安宁.由震中迁移交汇预测大震的讨论[J].地震工程学报，2016,38(1)： 1-3.

GUO Z J, GUO A N. Discussion on the prediction of large earthquakes based on the intersection of epicenter migration [J].ChinaEarthquakeEngineeringJournal, 2016,38(1)： 1-3.

[26] 韩延本,郭增建,吴瑾冰,等.太阳活动对中国近东西向断层8级大地震的可能触发[J].中国科学：G辑,2003(6)： 567-573.

HAN Y B,GUO Z J, WU J B, et al. The possible triggering of solar activity on the near east faultM8 earthquake in China [J].ScienceinChina：SerG，2003(6)： 567-573.

[27] 秦四清,徐锡伟,胡平,等.孕震断层的多锁固段脆性破裂机制与地震预测新方法的探索[J].地球物理学报,2010,53(4)： 1001-1014.

QIN S Q, XU X W, HU P, et al. Brittle failure mechanism of multiple locked patches in a seismogenic fault system and exploration on a new way for earthquake prediction [J].ChineseJournalofGeophysics，2010,53(4)： 1001-1014.

[28] 蒋伯琴.太阳黑子、磁暴与地震活动的关系[J].地震学报,1985(4)： 452-460.

JIANG B Q. The relationship among sunspots，magnetic storms and earthquakes [J].ActaSeismologicaSinica，1985(4)： 452-460.

[29] 李英杰，延军平，唐宝琪，等.美国圣安德烈斯断裂带强震活动规律及未来趋势研讨[J].中国地质灾害与防治学报，2016，27(4)： 56-63.

LI Y J, YAN J P, TANG B Q, et al. Tendency judgement ofMw≥6.8 earthquake in San Andreas fault[J].TheChineseJournalofGeologicalHazardandControl，2016,27(4)： 56-63.

[30] 陈学忠，李艳娥，王恒信，等.2004年印尼苏门答腊Mw9.0地震前地震活动增强现象及其与地球自转的关系[J].地球物理学学报，2013,56(1)： 79-90.

CHEN X Z, LI Y E, WANG H X, et al. The enhancement of seismicity before the 2004Mw9.0 Indonesia Sumatra earthquake and its relation to the earth rotation [J].ChineseJournalofGeophysics，2013，56(1)： 79-90.

[31] 马宗晋，陈章立，傅征祥，等.亚欧地震系的地震构造特征[J].中国科学：A辑，1980(9)： 883-890.

MA Z J, CHEN Z L, FU Z X, et al. The seismic structural characteristics of the Eurasian Seismotectonics [J].ScienceinChina：SerA，1980(9)： 883-890.

[32] 徐道一，郑文振，安振声，等.天体运行与地震预报[M].北京： 地震出版社，1980.

XU D Y, ZHENG W Z, AN Z S,et al.TheCelestialMovementandEarthquakePrediction[M]. Beijing： Seismological Press，1980.

[33] 延军平.时间地理学：动态地理学概论[M].西安： 陕西师范大学出版社，1994.

YAN J P.TimeGeography：AIntroductiontoDynamicGeography[M]. Xi’an： Shaanxi Normal University Press，1994.

WANG Hui1,2, YAN Junping1,2, TANG Baoqi1, LI Yingjie1
(1.SchoolofGeographyandTourism，ShaanxiNormalUniversity，Xi’an710119，China；2.NationalDemonstrationCenterforExperimentalGeographyEducation(ShaanxiNormalUniversity),Xian710119,China)

Space-timesymmetryandtendencyjudgementofMw≥6.9earthquakeinPeru.Journal of Zhejiang University (Science Edition)，2018, 45(1)： 001-009

Based on the seismic data (Mw≥6.9) in Peru, the signal intensity of the earthquakes tendency is analyzed and judged by the methods of commensurability information according to the theory of commensurability. The butterfly structure diagram, commensurability structure system and epicenter migration approach are employed to prove the reliability of the forecast result and reveal how the astronomical factors affect strong earthquake activities. It shows that the seismic activities ofMw≥6.9 in Peru since 1970 exhibit obvious commensurability, the tendency of an intermediate focus earthquake occurring in 2019 is strong with the random probability of 55.56%. Besides, the great earthquakes in Peru have a significant relationship with the solar activity，earth’s rotation and lunar movement： Previous earthquakes mostly occurred in the solar activity peak and decline period, the double cycle of sunspot and the years with variance of the Earth’s rotation rate; Earthquake unlikely occurred in full moon and twilight moon days.

commensurability; spatiotemporal symmetry; trend judgment; sunspot; earthquake

2017-04-07.

国家自然科学基金资助项目(41171090)；国家社会科学基金重点项目(14AZD094)；教育部人文社会科学重点研究基地重大项目(15JJD790022).

王辉(1990—)，ORCID： http： //orcid.org/0000-0003-4885-1608,男，博士研究生，主要从事灾害地理学与区域可持续发展研究，E-mail： fjwh1990@126.com.

*通信作者，ORCID： http： //orcid.org/0000-0003-3983-198X, E-mail： yanjp@snnu.edu.cn.

10.3785/j.issn.1008-9497.2018.01.001

P 954；X43

A

1008-9497(2018)01-001-09