混沌多时编码调相雷达波形设计
2018-01-08
(电子科技大学,四川成都611731)
混沌多时编码调相雷达波形设计
肖鸿博,吕幼新
(电子科技大学,四川成都611731)
单一调制的雷达信号的波形简单、变化少,使得雷达信号更容易被截获,抗干扰性能也较差。针对这一问题,设计了一种混沌多时编码与相位调制相结合的波形产生方法。首先根据线性调频信号的参数并按照多时编码规则产生一系列相位,每个相位状态持续时间不同;再对相位用混沌序列进行编码,使每个子脉冲具有不同的相位状态。仿真结果表明,两种混沌多时编码调相雷达信号的自相关旁瓣峰值最大值分别达到-27.92 dB和-27.60 dB,相比于只加入混沌编码调相的信号或多时编码信号,其相关性得到了极大提升。结果表明,混沌多时编码调相信号既继承了相位调制信号的优点,优化了功率谱,使其变得更平坦,同时又具有良好的抗噪声干扰性能和正交性,波形也更加复杂多变,是一种理想的雷达信号。
混沌;多时编码;调相;波形设计
0 引 言
现代战争中,雷达所面临的工作环境日渐恶劣,如何提高雷达的抗干扰性能显得尤为重要。现在的干扰主要分为两类:压制式和欺骗式。
现阶段的欺骗式干扰方法主要是利用数字射频存储器接收本方发射信号后,进行参数修改并转发来干扰。因此进行抗干扰,主要从两个方面着手:一是提高雷达的低截获性能;二是利用干扰信号与真实目标回波信号时间差异,使得雷达接收机与目标回波信号相匹配,与干扰信号失配,从而抑制各类干扰的影响。因此设计一系列波形,使得各个周期的信号具有随机性,每个周期的信号之间具有良好的正交性;每个周期发射不同波形,雷达接收机每个周期匹配函数也不同,使得目标信号匹配,干扰信号失配。
Deng[1-2]首先将优化计算方法应用于正交波形的设计中,将模拟退火算法进行优化,产生具有良好正交性的频率编码信号。Liu等[3-5]将遗传算法(Genetic Algorithm)应用于正交多相离散频率编码的波形设计中,大大降低了自相关旁瓣;其平均自相关为-16.7 dB,平均互相关为-13.64 dB。将混沌与波形的调频、调幅、调相相结合,则具有更加显著效果,Flores等[6]研究了混沌调频信号的性能,Xie等[7]将混沌编码与幅度、频率、相位调制结合,对产生的信号进行了性能研究。Zhao等[8]研究了混沌相位频率复合编码,设计出一种雷达信号,其自相关函数最大峰值大于-20 d B。Shen等[9]则将混沌编码与多相编码相结合,设计出具有良好正交性的雷达波形。
本文采用混沌编码、多时编码和相位联合调制用于线性调频信号(LFM)波形设计,结合调相信号的功率谱平坦特性和混沌信号随机性,使得信号的正交性得到提高,产生的雷达信号的自相关与互相关最大值均小于-27 d B,平均值均小于-40 dB,性能得到显著提升。
1 混沌系统
一般地,混沌现象指确定性动力学系统因对初值敏感而表现出的不可预测的、无规律的运动。混沌在统计特性上类似于随机过程。常见的混沌系统如下所示:
Tent序列:X(n)=T(X(n-1))=A-BX(n-1),初始值
X(1)∈[-1/2,1/2],X(n)∈(-1/2,1/2],A=1/2,B为自由参数,B=2-ε(ε→0)。
X(1)∈[-1/2,1/2],X(n)∈(-1/2,1/2],A=1/2,B为自由参数,B=4-ε(ε→0)。
X(1)∈[-1/2,1/2],X(n)∈(-1/2,1/2),A=1/2,B为自由参数,B=2-ε(ε→0)。
混沌系统由其初值和自由因子来确定后续变化,也因为混沌系统的初值敏感性,不同初值会得到完全不同的混沌序列,本文采用Quadratic混沌系统为例进行阐述。
2 多时编码
普通相位编码的每个相位状态所占用的时间是一个常量,而多时编码的每个相位状态在整个波形的持续时间内是变化的,每个相位状态的持续时间不同。多时编码具有n个相位状态,如下所示。
T1(n)码多时的折叠相位相对于时间表达式:

T2(n)码多时的折叠相位相对于时间表达式:

增加相位状态数可以提高基础波形多时近似的质量,但是也会降低每个给定相位状态所占用的时间,从而使得波形的产生复杂化。多时编码还具有几个相位状态能产生任意时间带宽的波形性质。
3 混沌多时编码调相信号
线性调频信号(LFM)广泛用于雷达的信号设计,本文以LFM信号为例,旨在设计一种结合混沌多时编码与相位调制相结合的雷达信号。
混沌多时编码调相信号表达式为

式中,f0为载波频率,φ0为调制相位。
对信号幅度进行归一化,其复包络为

式中,X(t)为混沌信号,ϕT1(t)为多时编码折叠相位。
对u T-PM进行离散化处理,离散后的信号复包络表达式为
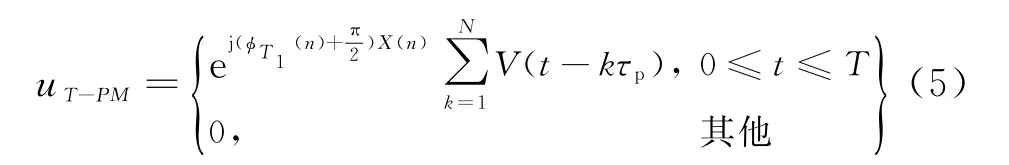
式中,x(n)为混沌序列,ϕT1(n)为多时编码折叠相位序列,长度均为N,T=Nτp为混沌调制宽度,V(t)为子脉冲函数,τp为子脉冲宽度,且
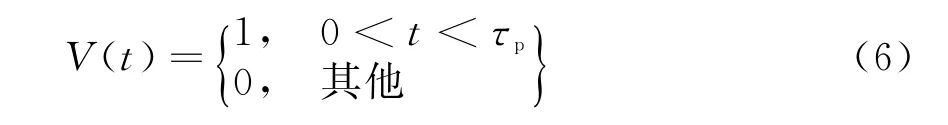
由此可推出
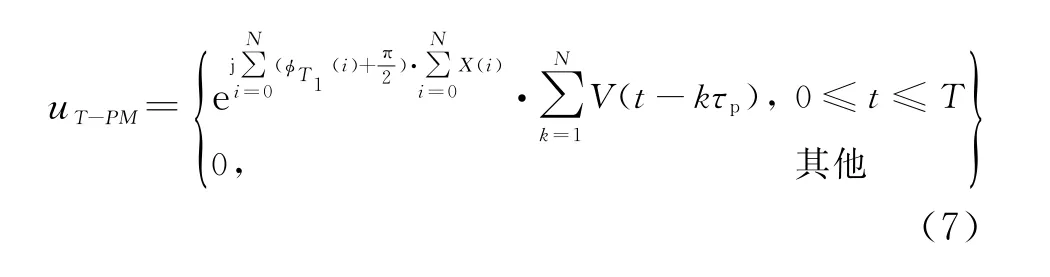
Quadratic混沌系统以初始值x(0)经过N次迭代后的序列为

因为混沌系统具有多值遍历性,不利于雷达信号的实现,所以需要对混沌序列进行量化,量化方式如下,混沌序列的均值为

由此均值对混沌序列进行二值量化:

可以推出
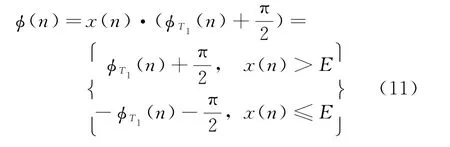
式中,ϕ(n)为最终调制相位。
自相关函数、互相关函数是评判雷达信号优劣的重要标准,上述雷达信号的自相关函数表达式为
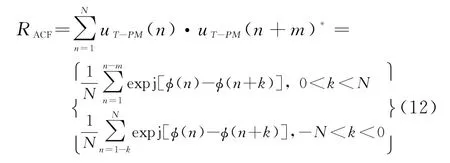
互相关函数的表达式为

4 仿真分析
该仿真在Matlab 2014a环境下进行,仿真实验数据:信号载频3 GHz,脉冲持续时间40μs,编码长度4 000,多时编码相位状态数n=5。
本文首先采用两种多时编码方式,计算出各个时延的折叠相位,如图1、图2所示。
可以看出,多时编码的5个折叠相位状态在各个不同时延持续的时间不同。然后采用Quadratic混沌迭代10 000次后生成混沌序列:
{x(1),x(2),…,x(9 999),x(10 000)}(14)式中,x(0)=0.1,ε=0.001。因为初值不同不会影响自相关最低旁瓣,本文所产生的混沌序列如图3所示。

图1 T1码折叠相位
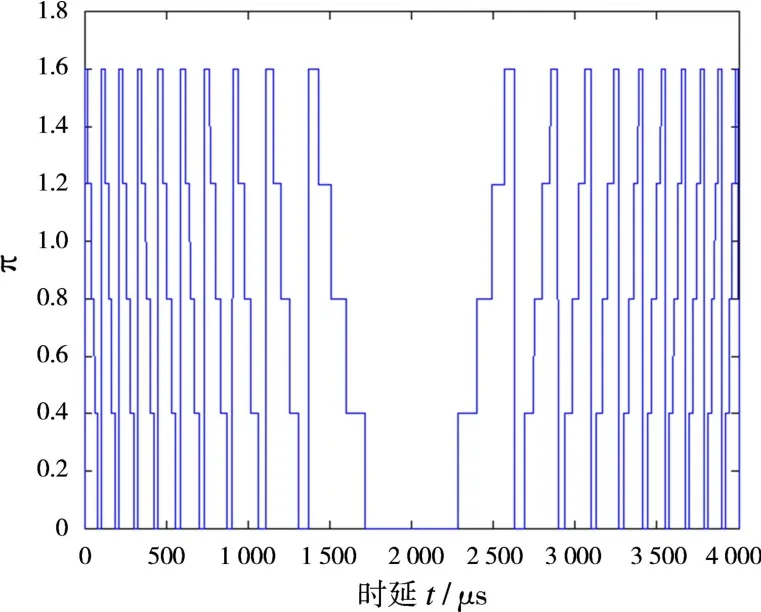
图2 T2码折叠相位
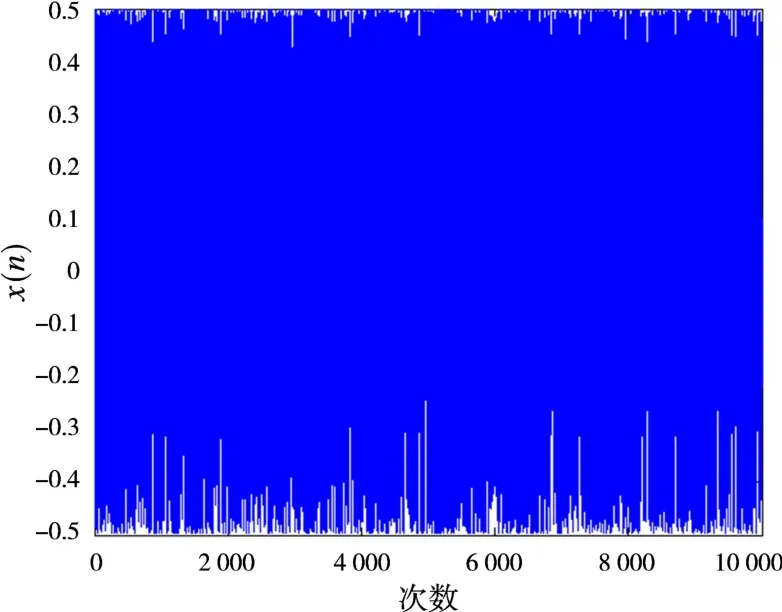
图3 Quadratic迭代10 000次的序列
4.1 相关性分析
将Quadratic序列与多时编码相结合所产生信号的自相关、互相关函数依次如图4~7所示。从图4、图5可以看出,混沌多时编码调相信号具有尖锐的自相关函数,最大自相关旁瓣峰值在-27.5 d B以下,自相关函数旁瓣平均值均在-42 d B以下。互相关函数均值均在-45 dB以下,是非常理想的信号。表1为Quadratic序列结合两种多时编码的归一化自相关峰值最大值(Max ASP)、自相关旁瓣峰值平均值(Aver ASP)、互相关峰值最大值(Max CP)、互相关峰值平均值(Aver CP)。
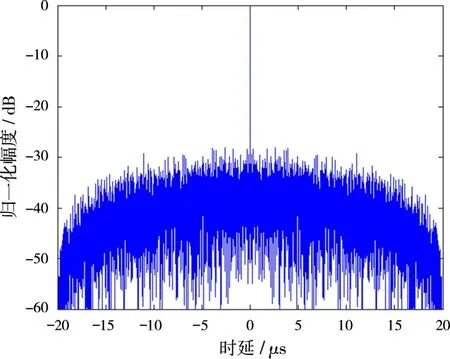
图4 混沌T1信号自相关
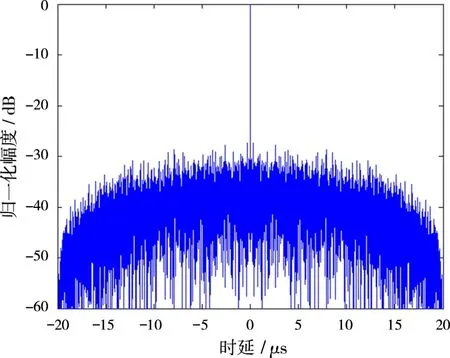
图5 混沌T2信号自相关
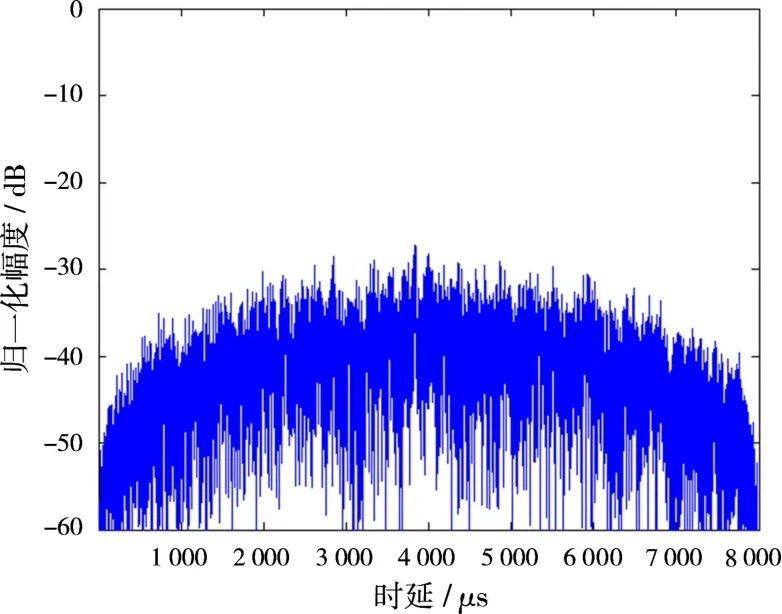
图6 混沌T1信号互相关
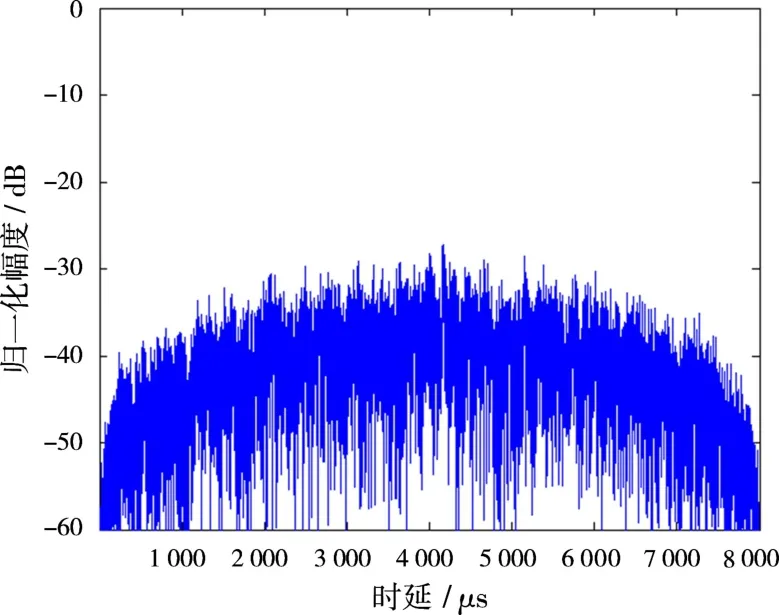
图7 混沌T2信号互相关
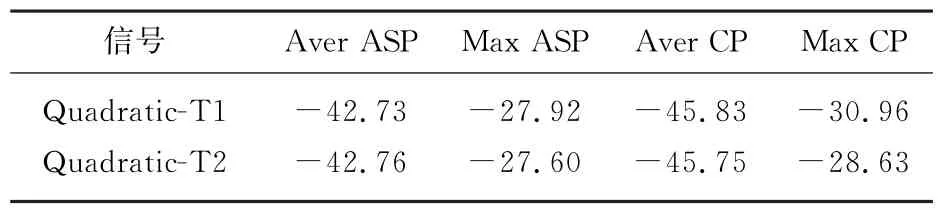
表1 两种波形相关性比较 dB
4.2 功率谱分析
功率谱与低截获性能息息相关,功率谱越平坦,雷达信号越难截获。Quadratic-T1、Quadratic-T2信号的功率谱如图8、图9所示。
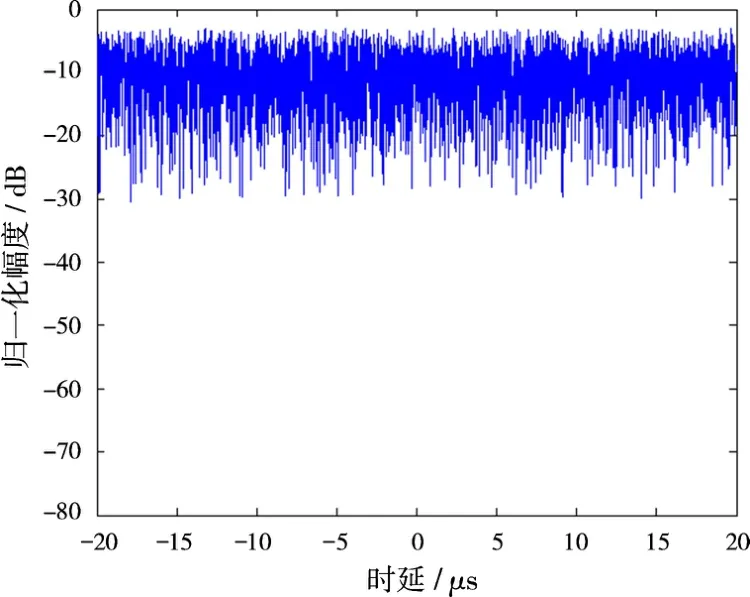
图8 Quadratic-T1功率谱
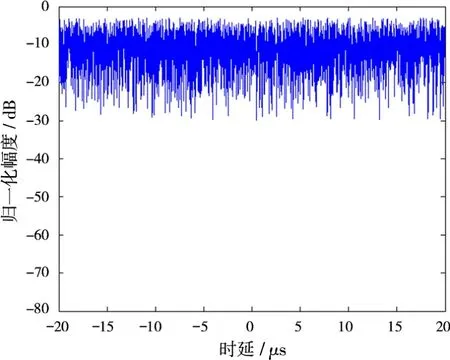
图9 Quadratic-T2功率谱
Quadratic-T1信号的功率谱波动在-32~-4 dB之间,平均功率为-13.04 dB。Quadratic-T2信号的功率谱波动在-33~-4 dB之间,平均功率为-13.58 dB。虽然波动范围仍然较大,但相对于一般的线性调频信号已经有相当程度的优化。
4.3 抗噪声性能分析
背景噪声为高斯分布白噪声,信号加入噪声后的信号模型为

信号传播损失系数为-10 dB,接收端输入信号信噪比(SNR)为-22 d B,匹配输出信号如图10所示。可知,能够很好地将目标检测出来,所以混沌多时编码调相信号具有很好的抗噪声性能。
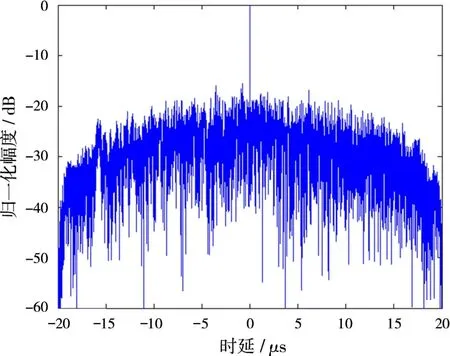
图10 抗噪声性能仿真
5 结束语
本文设计了一种混沌多时编码结合相位调制的波形产生方法。这种波形具有尖锐的自相关函数及良好的正交性。从功率谱上看,它优于传统信号,相对更加平坦;从抗噪声性能上看,它能够清晰分辨目标,性能良好。仿真结果表明,混沌多时编码调相雷达信号波形更加复杂,比单一调制的信号具有更高的不可预测概率和低截获概率,同时有效提高了抗干扰性能。
基于混沌序列和多时编码,将其与幅度、相位、频率调制相结合的波形设计还有很大的研究空间。
[1]DENG H.Discrete Frequency-Coding Waveform Design for Netted Radar Systems[J].IEEE Signal Processing Letters,2004,11(2):179-182.
[2]DENG H.Polyphase Code Design for Orthogonal Netted Radar Systems[J].IEEE Trans on Signal Processing,2004,52(11):3126-3135.
[3]LIU B,HE Z,HE Q.Optimization of Orthogonal Discrete Frequency-Coding Waveform Based on Modified Genetic Algorithm for MIMO Radar[C]∥International Conference on Communications,Circuits and Systems,Kokura:IEEE,2010:966-970.
[4]LIU B,HE Z,ZENG J,et al.Polyphase Orthogonal Code Design for MIMO Radar Systems[C]∥CIE International Conference on Radar,Shanghai:IEEE,2006:1-4.
[5]LIU B,HE Z.Genetic Algorithm Based MIMO Radar Polyphase Code Design[J].Journal of Electronic Measurement and Instrument,2008,22(2):62-66.
[6]FLORES B C,SOLIS E A,THOMAS G.Assessment of Chaos-Based FM Signals for Range-Doppler Imaging[J].IEE Proceedings:Radar,Sonar and Navigation,2003,150(4):313-322.
[7]XIE S,HE Z,PAN J.Antinoise Performances of Improved Tent Chaos-Based Phase Modulation Radar Signal[J].Information Technology Journal,2012,11(8):1115-1120.
[8]ZHAO J,HUO K,LI X.A Chaos-Based Phase-Coded OFDM Signal for Joint Radar-Communication Systems[J].12th International Conference on Signal Processing,Hangzhou:IEEE,2014:1997-2002.
[9]SHEN D,ZHANG L,LIU X,et al.Polyphase Orthogonal Code Waveform Design Based on Chaotic Sequences for MIMO Radar[J].Journal of Lanzhou University(Natural Sciences),2011,47(1):100-105.
[10]LEI C.Radar Waveform Design Research Based on Chaos[D].Chengdu:University of Electronic Science and Technology of China,2011:30-54.
[11]周云,卢霞霞,于雪莲,等.基于混沌的调频调相的多输入多输出雷达正交波形设计[J].计算机应用,2015,35(12):3357-3361.
[12]吴健,崔国龙,孔令讲.一种抗速度欺骗干扰的认知波形设计方法[J].雷达科学与技术,2015,13(2):133-138.
Radar Waveform Design of Joint Phase Modulation Based on Chaos and Multi-Times
XIAO Hongbo,LYU Youxin
(University of Electronic Science and Technology of China,Chengdu611731,China)
The single modulation radar waveform has low complexity,which limits the low interception and anti-interference performance of radar.The joint phase modulation based on chaos and multi-times in radar waveform is proposed to solve this problem.Firstly,the multi-times encoding is generated by the parameters of LFM signal and the duration of each phase is different.Then,the chaotic sequence is used to encode the phase,which makes each sub-pulse have different phase states.Simulation results show that the maximum ACF values of the two signals through different chaotic and multi-times coding modulations reach-27.92 dB and 27.60 dB respectively.Its correlation performance has been greatly improved.The experimental results show that the joint phase modulation based on chaos and multi-times in radar waveform inherits the advantages of phase modulated signals,and optimizes the power spectrum,and increases the ability to counter noise and interference.The waveform has more complexity.
chaos;mutil-times coding;phase modulation;waveform design
TN974
A
1672-2337(2017)02-0166-05
10.3969/j.issn.1672-2337.2017.02.010
2016-07-27;
2016-09-18

肖鸿博男,1991年出生,硕士,主要研究方向为雷达信号处理。
E-mail:xiaohb_work@163.com
吕幼新男,1963年6月出生,硕士,现为电子科技大学教授、“信号与系统”课程首席教师,主要从事雷达信号理论、高速实时信号处理领域的教学与科研工作。
