基于曲率估计的Canny边缘检测算法①
2018-01-08郑子华陈家祯
郑子华,陈家祯,叶 锋,2
1(福建师范大学 数学与计算机科学学院,福州 350007)
2(福建星网锐捷通讯股份有限公司,福州 350002)
基于曲率估计的Canny边缘检测算法①
郑子华1,陈家祯1,叶 锋1,2
1(福建师范大学 数学与计算机科学学院,福州 350007)
2(福建星网锐捷通讯股份有限公司,福州 350002)
为了解决传统Canny边缘检测算法对噪声敏感的问题,针对噪声边缘弯曲度大且弯曲空间范围小的二维空间特性,构造了基于曲线曲率估计的边缘曲度算子,并利用大尺度Canny算法边缘检测结果对边缘曲度算子进行修正,使该算子能够准确地表征噪声强度在二维空间中的分布情况,在此基础上,提出了一种在边缘检测过程中加入边缘曲度算子进行噪声衰减的边缘检测算法. 实验结果表明,算法在有效抑制噪声的同时,保留了变化丰富的细节边缘及变化缓慢的轮廓边缘,检测结果较好地反映了图像的原始结构特征.
边缘检测; Canny 算子; 尺度; 噪声抑制; 曲率估计
图像边缘是图像基本特征之一,它蕴含了图像丰富的内在信息(如方向,阶跃性质与形态等),广泛用于图像分割、图像分类、图像配准和模式识别中[1],因此,边缘检测成为图像处理中一个十分重要的环节. 除了传统的边缘检测算子如Roberts、Sobel、Prewitt算子等,近年来,随着边缘检测技术不断被广泛深入地研究,新的理论工具被引入到该领域,各种边缘检测方法相继产生,例如: 基于小波分析的方法[2]、基于统计学的方法[3]、基于模糊理论的方法[4]、基于神经网络的方法[5]、基于遗传算法的方法[6]、基于支持向量机的方法[7]等等.
1986年Canny用3个判断准则对阶跃边缘检测问题进行了统一: 信噪比准则; 定位精度准则; 对单一特征响应的唯一性准则,并由此推导出了最佳边缘检测的Canny算子[8]. Canny算子因为在边缘检测方面获得的良好效果及其计算的高效性,很快就成为了其它边缘检测算法的比较标准. 然而,应该指出的是,Canny算法是寻找阶跃边缘模型的最佳检测算法,当遇到变化缓慢的模糊边缘,受噪声污染的边缘、或者整幅图像范围内亮度或对比度不一致时,检测结果就不甚理想. 传统Canny算法在单一尺度下仅依据梯度幅值判定像素点是否为边缘点,这种做法会造成算法在抑噪性和保边缘性两方面能力的对立: 当滤波器滤波尺度较小时,能检测到弱小的边缘且边缘定位精度高,但对噪声却非常敏感; 当滤波器滤波尺度较大时,虽然算法对噪声抑制能力得到增强,却失去了检出弱小边缘的能力,且检测到的边缘存在定位精度低的问题. Canny算法的高效性及其固有的缺陷引发了大量研究者的兴趣,在传统Canny算法架构下,改进的方法不断被提出[9-13].
鉴于传统Canny算法的弱抑噪性,本文根据噪声边缘的二维空间特性,提出了一种能够有效量化描述边缘弯曲程度的边缘曲度算子,将其作为描述边缘与伪边缘之间差异的特征信息,并利用大尺度边缘信息对边缘曲度算子进行修正,使该算子能够准确体现图像噪声强度在二维空间中的分布情况. 最后,利用边缘曲度算子图对噪声进行衰减从而提取边缘. 本文方法既达到很好的抑噪效果,又能较完整地保留图像的细节边缘和轮廓边缘,是传统Canny算法的有益补充.
1 传统的 Canny 边缘检测算法[8]
根据文献[8]中的内容,传统Canny边缘检测算法过程可如1.1至1.4节所述.
1.1 平滑图像
Canny算法首先用二维高斯函数对图像进行平滑,设二维高斯函数为:
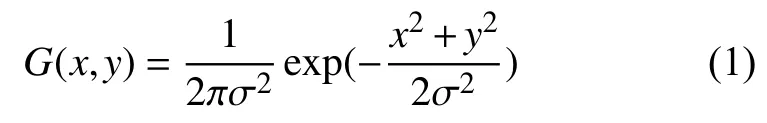
其中,σ为高斯滤波器参数,它控制着平滑程度.
1.2 计算梯度幅值和梯度方向
平滑后的数据阵列I(x,y)的梯度幅值和梯度方向分别为:
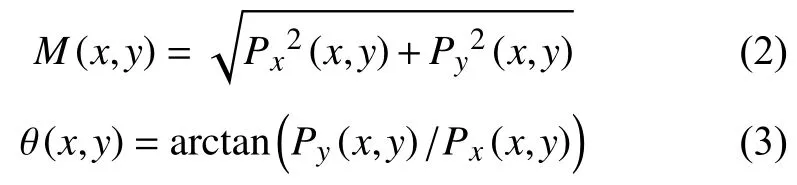
其中,x 和y 方向偏导数分别为:
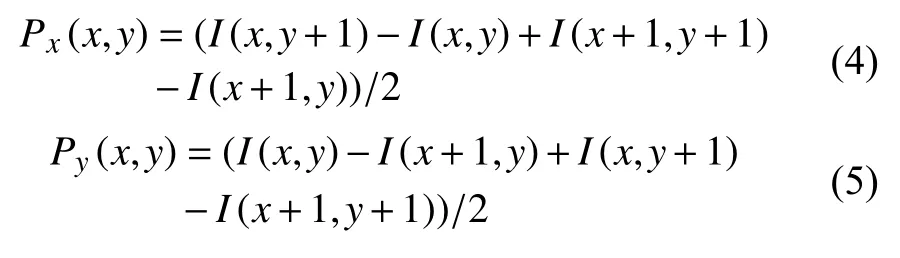
1.3 非极大值抑制
遍历梯度幅值图M,在以M(x,y)为中心点的8邻域内判断,如果M(x,y)比梯度方向上相邻两个点的幅值都大,则令M1(x,y)=M(x,y),否则,令M1(x,y)=0.M1为非极大值抑制结果.
1.4 双阈值法检测并连接边缘
具体步骤为:分别使用高阈值Thmax和低阈值Thmin对图像M1 进行判断,若M1(x,y)>Thmax,则判定该点是边缘点,若M1(x,y)
2 基于曲线曲率估计的边缘曲度算子
图1为传统Canny算法对加入椒盐噪声的图像的检测结果.

图1 有噪图像 Canny 算法检测结果
如图1所示,噪声被误作为边缘检出时,基本呈现弯曲程度大且弯曲空间范围小的二维空间特性,与真实边缘轮廓完全不同. 文献[13]利用此特性,采用了在7×7邻域内确定质心m,然后计算质心m、邻域中心o与邻域中的边缘点x所构成的三角形的三条边的长度的平方,最后根据余弦定理计算边缘点x到直线om的投影距离,并通过该投影距离来衡量边缘弯曲程度. 文献[13]取得了良好的检测效果,但仍存在部分有意义的轮廓边缘被漏检的问题,如文献[13]有噪声条件下的检测结果中摄像师的手及远处建筑物的部分轮廓被漏检,而这些漏检信息在后续的图像处理中可能非常重要. 本文将定义基于曲线曲率估计的边缘曲度算子,该算子利用梯度方向夹角来估计曲率,计算简单,物理意义明确,适用于表征局部边缘的弯曲程度,同时,利用大尺度下Canny算子边缘检测结果对边缘曲度算子进行修正,有利于保留小尺度下易被漏检的模糊边缘及与噪声混淆的细节边缘.
2.1 微分几何中曲线曲率的定义
如图2所示,在光滑曲线CD上点A和临近一点A’各做一条切线,A和A’之间的弧长为ΔS,两条切线夹角为α,则曲线CD在A点的曲率K定义为[14]:

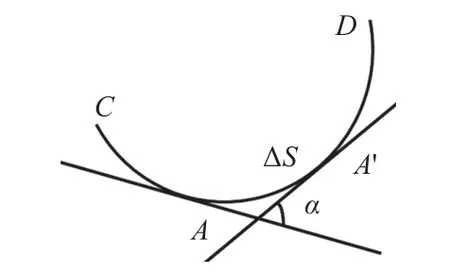
图2 曲线曲率的定义
一些研究者利用曲率进行边缘检测,如文献[15]将像素曲率视作特征视图之一,用于提取图像边缘; 文献[16]则是利用曲面曲率进行屋脊边缘检测,并可以判断屋脊边缘是上凸型还是下凹型. 但是,不管是利用曲线曲率还是曲面曲率进行边缘检测,由于曲率计算公式比较复杂,最终将会导致相关算法计算量较大,不利于算法处理的实时性. 基于此,本文不直接利用曲线曲率作为表征边缘弯曲程度的依据. 在对曲线曲率的概念做进一步定量分析后,可得到以下两个结论,下面结合图3、图4对两个结论进行说明.
结论一. 切线夹角相同的条件下曲线越短则曲线弯曲程度越大.
如图3所示,切线夹角α 既对应着B1与B2之间的弧长ΔS3,也对应着C1与C2之间的弧长ΔS4,其中,ΔS3 弧长小于ΔS4 弧长,从图3 中可以看出,ΔS3 的弯曲程度明显大于ΔS4的弯曲程度.
结论二. 在弧长长度相等的情况下,切线夹角越大则曲线弯曲程度越大.
如图4所示,过A1点的切线与过A2点的切线相交所得切线夹角α2对应着A1与A2之间的弧长ΔS2,过A2点的切线与过A3点的切线相交所得切线夹角α1对应着A2与A3之间的弧长ΔS1,其中,ΔS1弧长与ΔS2 弧长相等,α1 >α2,从图4 中可以看出,ΔS1 的弯曲程度明显大于ΔS2的弯曲程度.
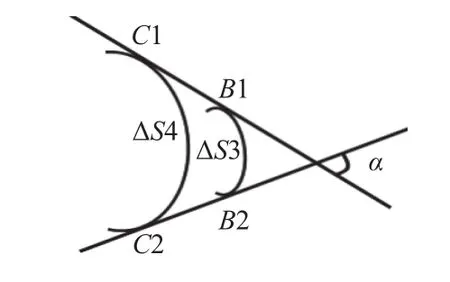
图3 结论一示例图
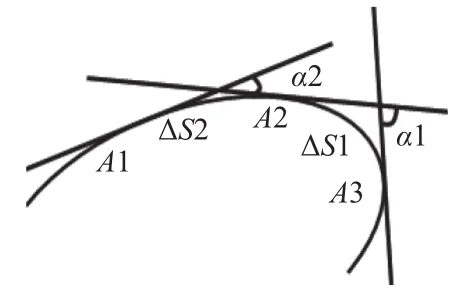
图4 结论二示例图
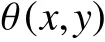
2.2 边缘曲度算子的定义
在2.1节分析的基础上,本文定义表征边缘弯曲程度的边缘曲度算子,记为CURV(x,y). 对二值边缘图K中每个点K(x,y),当K(x,y)=0 时,为非边缘点,CURV(x,y)=0; 当K(x,y)=1 时,为边缘点,可用如下步骤来计算该点对应的CURV(x,y).
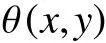
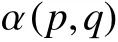
当 K(p,q)=0 时,K(p,q)为非边缘点,α(p,q)=0
当K(p,q)=1 时,K(p,q)为边缘点,则令
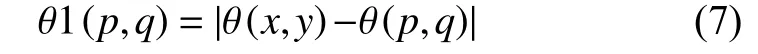
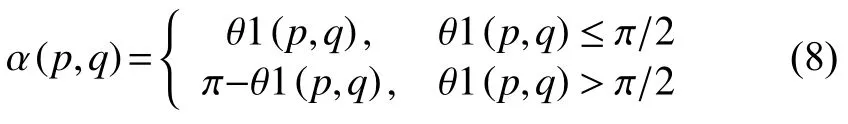
(3) 计算SURV(x,y),如式 (9).

(4) 对SURV进行归一化处理.
3 单尺度下边缘曲度算子的不足与修正
图5为单一小尺度下 σ=1边缘曲度算子归一化图CURV,如图5所示,二维空间上灰度值的差异准确地体现了噪声强度在二维空间上的分布,是下一步对图像噪声进行精确衰减的依据. 有一点不足的是: 在CURV中,除了噪声的位置以高灰度值被标注出以外,一些细节边缘的位置也被以低灰度值的形式微弱地标注出来,如摄影师的脸部、相机等,这部分边缘被CURV标注成微弱噪声,虽然标注的灰度值很低,但对后续这部分有效边缘的检出不利,为了提高边缘检测的信噪比,必须进行修正.

图5 归一化后的CURV
对于这个问题,本文采用大尺度边缘图进行辅助修正. 大尺度边缘图上较少有噪声干扰,但其检出的边缘定位不精确,可用于对小尺度下CURV是否正确标记噪声的位置及强度进行辅助判断. 具体步骤如下:
(1) 利用传统Canny算法求取大尺度边缘图,记为:KMAX,通常情况下取 σ=2.
(2) 遍历小尺度下CURV,当CURV(x,y)≠0 时,检查KMAX(x,y)的 3×3 邻域内是否存在边缘点,如存在边缘点,则令CURV(x,y)=0; 反之,CURV(x,y)保持原值.
修正后的CURV如图6所示,可以看出,之前被微弱标注的边缘(如摄影师的脸部、相机等)基本从CURV中被剔除,解决了修正前存在的问题.

图6 修正后的CURV
4 基于曲率估计的Canny边缘检测算法
在以上分析的基础上,本文提出一种基于曲率估计的Canny边缘检测算法,该算法的主要思想是: 首先利用传统的Canny算法分别对含噪图像检出大小两种尺度下的两幅边缘图,根据噪声边缘的二维空间特性,利用小尺度边缘图计算出边缘曲度算子归一化图CURV,并利用大尺度边缘图进行修正,使CURV能准确表征小尺度下噪声强度在二维空间上的分布情况.然后,用Canny算法小尺度下归一化后的非极大值抑制结果与CURV相减,达到在小尺度上进行噪声衰减的目的,最后,把衰减后的结果利用双阈值法判定出边缘图. 算法主要流程如图7所示.
为了细化算法的主要思想和流程,现将算法的具体步骤详细描述如下:
(1) 根据第1节描述的传统Canny边缘检测算法,取 σ=2,计算原始图像的边缘图,记为:KMAX;
(2) 根据第1节描述的传统Canny边缘检测算法,取 σ=1,计算原始图像的边缘图,记为:KMIN,并保留第1.3节描述的非极大值抑制的计算结果,记为M1;
(3) 根据第2.2节描述的具体步骤,对KMIN求取CURV;
(4) 根据第3节描述的具体步骤,利用KMAX对CURV进行修正;
(5)K=M1-CRUV;
(6) 根据第1.4节描述的双阈值法对K进行边缘判断,得到最终的边缘检测结果.
以上步骤(1)、(2)、(6)中,边缘提取时采用双阈值法,高阈值设为:Thmax=a×th; 低阈值设为:Thmin=b×th,其中th为初始阈值,th的确定方法参照Canny算法: 在待处理图的直方图分布中,像素点个数按图的像素值递增的方向累加,累加个数达到总像素数的0.7时,对应的像素值作为初始阈值,记为th. 可见,th是自适应的.a和b这两个系数是通过大量的实验数据确定出的经验值. 步骤 (1)中,a=1.5,b=0.4,这是由于大尺度边缘图只是用于辅助判断,适当提高a可减少噪声点的检出; 步骤 (2)中,a=1,b=0.4; 步骤 (6)中,a=12,b=0.4. 比起步骤(1)和步骤(2),步骤(6)中K的直方图中有更多的像素点集中在更低的像素值区中,因此,系数a的取值要比前两个步骤大得多.

图7 算法流程图
5 实验结果
为了验证本文所提算法的有效性,本文以一台配置为: Intel 2.6 GHz CPU、4 GB 内存、Microsoft Windows7 64 位操作系统,并安装 Matlab R2013a 软件的计算机为实验平台,对三幅典型测试图像加入不同类型的噪声后进行边缘检测.
cameraman.bmp为256×256像素、256灰度级灰度图; lena.bmp为256×256像素、128灰度级灰度图;peppers.tiff为 512×512 像素、256 灰度级灰度图,对加噪后的灰度图边缘检测结果如图8至图11所示. 图8(a)为cameraman.bmp、lena.bmp、peppers.tiff加密度为0.02椒盐噪声的加噪图; 图9(a)为 cameraman.bmp、lena.bmp、peppers.tiff加 σ=0.02高斯白噪声的加噪图; 图10(a)为 cameraman.bmp、lena.bmp、peppers.tiff加方差为0.02乘性噪声的加噪图. 图8(b)、图9(b)、图10(b)分别为Canny算法在 σ=1时对图8(a)、图9(a)、图10(a)进行边缘检测的结果;图8(c)、图9(c)、图10(c)分别为本文算法对图8(a)、图9(a)、图10(a)进行边缘检测的结果. 图11(a)是cameraman.bmp加密度为0.02椒盐噪声的加噪图,图11(b)、(c)分别是文献[13]算法和本文算法对图11(a)的检测结果.

图8 加椒盐噪声图检测结果比较
检测256×256像素灰度图,传统Canny算法平均耗时0.1101秒,本文算法平均耗时0.3862秒; 检测512×512像素灰度图,传统Canny算法平均耗时0.2264秒,本文算法平均耗时0.9753秒. 由于本文算法对传统的Canny算法做了较多的优化步骤,因此在检测时间上比传统的Canny算法耗时更多.
如图8至图11所示,本文算法对加有不同类型噪声的不同图像进行边缘检测,其检测结果都明显优于传统的Canny算法. 噪声和无意义的细微纹理均被抑制,而原始图像中变化缓慢的轮廓边缘和体现细节的边缘被保留下来,前者如图8(c)、图9(c)、图10(c)中摄像师的手、远处建筑物的轮廓、背景的立柱等,后者如图8(c)、图9(c)、图10(c)中摄像师的脸部、相机等,可见,原始图像的各种信息在本文算法检测结果中得到较完整的保留. 在与文献[13]检测结果的对比中同样也体现出本文算法能较好地保护缓慢变化的轮廓边缘,具体详见图11. 对不同的加噪图检测结果都良好,也说明算法中阈值系数设置具有一定的合理性,最后,由于本文算法所得的检测数据都来自于Canny算法小尺度上,这就决定了本文算法的最终边缘检测结果具有较高的定位精度.

图9 加高斯白噪声图检测结果比较

图10 加乘性噪声图检测结果比较

图11 本文算法与文献[13]算法的比较
6 结束语
本文利用曲线曲率概念下定量分析的结论,定义了基于曲率估计的边缘曲度算子,该算子能体现边缘的弯曲程度,从而表征噪声强度在二维空间上的分布情况,在此基础上,提出了一种基于该算子的Canny边缘检测算法. 实验结果表明,本文算法解决了传统Canny边缘检测算法对噪声敏感的问题,有效抑制了图像中的噪声,保护了变化丰富的细节边缘及变化缓慢的轮廓边缘,且具有较高的边缘定位精度. 当然,本文算法也存在不足之处: 其一,尽管本文算法对十幅加有不同类型噪声的不同图像均有良好的检出结果,说明了算法的有效性和算法中阈值系数设置的合理性,但是,阈值系数a和b是根据经验值来设定的,并不是自适应生成的,另外,本文算法的平均耗时比传统Canny算法有了一定的增加. 下一步将在如何自适应生成阈值系数及如何提高算法效率两方面做进一步分析和研究.
1李弼程,彭天强,彭波. 智能图像处理技术. 北京: 电子工业出版社,2004: 149.
2Desolneux A,Moisan L,Morel JM. Edge detection by helmholtz principle. Journal of Mathematical Imaging and Vision,2001,14(3): 271–284. [doi: 10.1023/A:101129023 0196]
3Konishi S,Yuille A,Coughlan J. A statistical approach to multi-scale edge detection. Image and Vision Computing,2003,21(1): 37–48. [doi: 10.1016/S0262-8856(02)00131-2]
4Kim DS,Lee WH,Kweon IS. Automatic edge detection using 3 × 3 ideal binary pixel patterns and fuzzy-based edge thresholding. Pattern Recognition Letters,2004,25(1):101–106. [doi: 10.1016/j.patrec.2003.09.010]
5王铮,李兴民. 基于四元数和SOM神经网络的彩色图像边缘检测. 计算机应用,2012,32(2): 510–513.
6李映,焦李成. 基于自适应免疫遗传算法的边缘检测. 中国图象图形学报,2003,8(8): 890–895. [doi: 10.11834/jig.200308332]
7刘涵,郭勇,郑岗,等. 基于最小二乘支持向量机的图像边缘检测研究. 电子学报,2006,34(7): 1275–1279.
8Canny J. Computational approach to edge detection. IEEE Trans. on Pattern Analysis and Machine Intelligence,1986,PAMI-8(6): 679–698. [doi: 10.1109/TPAMI.1986.4767851]
9Ray K. Unsupervised edge detection and noise detection from a single image. Pattern Recognition,2013,46(8):2067–2077. [doi: 10.1016/j.patcog.2013.01.029]
10Zhang XC,Liu CC. An ideal image edge detection scheme.Multidimensional Systems and Signal Processing,2014,25(4): 659–681. [doi: 10.1007/s11045-013-0224-9]
11Shui PL,Zhang WC. Noise-robust edge detector combining isotropic and anisotropic Gaussian kernels. Pattern Recognition,2012,45(2): 806–820. [doi: 10.1016/j.patcog.2011.07.020]
12张桂梅,孙晓旭,陈彬彬,等. 结合分数阶微分和 Canny 算子的边缘检测. 中国图象图形学报,2016,21(8): 1028–1038. [doi: 10.11834/jig.20160807]
13徐德明,万长林. 可抗噪声的Canny改进边缘检测算法. 计算机系统应用,2017,26(1): 201–205. [doi: 10.15888/j.cnki.csa.005581]
14沈永欢,梁在中,许履瑚,等. 实用数学手册. 北京: 科学出版社,2004: 393.
15张衡,谭晓阳,金鑫. 基于多视图聚类的自然图像边缘检测. 模式识别与人工智能,2016,29(2): 163–170.
16杨海军,梁德群. 基于曲率的屋脊边缘检测方法. 模式识别与人工智能,2000,13(2): 210–213.
Canny Edge Detection Algorithm Based on Curvature Estimation
ZHENG Zi-Hua1,CHEN Jia-Zhen1,YE Feng1,2
1(School of Mathematics and Computer Science,Fujian Normal University,Fuzhou 350007,China)
2(Fujian STAR-NET Communications Co. Ltd.,Fuzhou 350002,China)
In order to solve the noise sensitive problem in the traditional Canny edge detection algorithm,based on the curvature estimation of curve,the edge curvature degree operator is constructed according to the noise edge characteristics which are large curvature and small curved space. The edge curvature degree operator is modified with the results of edge detection of the large scale Canny algorithm so that the operator can accurately characterize the distribution of the noise intensity in the two-dimensional space. On this basis,an edge detection algorithm based on edge curvature degree operator is proposed and the edge curvature degree operator can restrain the noise. The experimental results show that the algorithm cannot only suppress the noise effectively,but can also preserve the rich details edges and the slowly changing contour edges,and the detection results show the original structural features of the image.
edge detection; Canny operator; scale; noise suppression; curvature estimation
郑子华,陈家祯,叶锋.基于曲率估计的Canny边缘检测算法.计算机系统应用,2017,26(12):148–154. http://www.c-s-a.org.cn/1003-3254/6139.html
福建省自然科学基金面上项目(2017J01739); 福建省教育厅项目(JA15136); 福建师范大学教改重点项目(I201601004); 福建师范大学教改项目(I201602015)
2017-03-23; 修改时间: 2017-04-20; 采用时间: 2017-04-26
