双交叉算子遗传算法在终端区飞机排序中的应用①
2018-01-08赵俨,乐俊,刘丹
赵 俨,乐 俊,刘 丹
1(电子科技大学 电子科学技术研究院,成都 611731)
2(西南电子电信技术研究所,成都 610041)
双交叉算子遗传算法在终端区飞机排序中的应用①
赵 俨1,乐 俊2,刘 丹1
1(电子科技大学 电子科学技术研究院,成都 611731)
2(西南电子电信技术研究所,成都 610041)
当今,普遍的航班延误现象不仅增加了巨额飞行成本,还影响乘客体验. 对终端区待降飞机队列进行合理调整,可以提高跑道利用率,减少航班延误,达到降低延误代价的效果. 针对终端区飞机排序问题,提出一种包含双交叉算子的遗传算法,针对不同适应度染色体采取不同的交叉操作,使得在交叉过程中既能保护优质染色体,也能使其它染色体继续进化. 同时引入重排算子对变异后的子代进行优化,共同加快遗传算法收敛速度,使其更加符合实际使用需求. 实验结果表明,算法收敛速度得到改进,能在可接受时间内得到可行解.
空中交通管制; 终端区; 飞机排序; 遗传算法; 交叉算子
随着国际民航运输的高速发展,我国对民航运输的需求日益提高,飞行器的数量也随之增加. 伴随空中交通流量的快速增长,机场、空域和航线普遍出现了拥堵现象. 2016年我国民航平均航班正常率为76.76%,较前两年虽有回升,但与美、日等国比较,仍有较大差距. 终端区拥堵不仅造成航班延误,还会存在安全隐患,引发安全事故. 通过对终端区飞机队列的合理排序,可有效的提高跑道容量,缓和拥堵,进而减少飞机延误[1].
目前,国内常用的飞机排序方式是先到先服务算法,即仅根据飞机的预计到场时间进行排序. 该算法的优势在于实现简便、易操作,但会产生较大的延误代价. 此外,较常见的排序算法还有滑动窗优化算法[2]、约束位置交换算法[3]、时间提前量算法[4]和模糊模式识别算法[5]等确定性优化算法. 但随着飞机数量的增加,确定性优化算法难以在可接受的时间内得出高复杂度排序问题的结果. 终端区飞机排序问题已被归为NP难问题,使用常规算法求最优解已不切实际.
1975年由Michigan大学的John Holand教授与其同事提出的遗传算法 (Genetic algorithm,GA)[6]具有良好的全局搜索能力、潜在并行性、可扩展性等优点,适合用于解决此类问题. 许多科研人员通过对传统遗传算法进行改进并融入其他算法或约束条件,提出了许多针对飞机排序的算法. 常会贤、曲世茹利用矩阵编码为飞机队列在多跑道降落的问题提出解决方案[7];白重阳等人利用遗传算法对飞机的速度进行调整,使得飞机在终端区航路冲突极小,从而减少飞机延误[8].陈亮等人对飞机延误代价系数的计算进行了讨论,指出代价系数会根据飞机类型和等待时间等因素的影响而动态改变. 根据该系数得出的飞机延误总代价模型更具有实际意义,而不再是片面的考虑如何将总延误时间降至最低[9].
在飞机排序的实际应用场景中,要求在可接受的时间范围内得到可以减少飞机延误的飞机排序队列.这不仅对排序质量有要求,排序的效率也不可忽视. 本文主要受文献[10]中提出的“交叉掩码”的概念和使用方式的启发,采取针对不同适应度的染色体采用双交叉算子分别处理的方式,达到既能保证优质染色体平稳进化,又不会影响其他染色体的进化速度的目的,使种群进化方向更加明确,从而加快算法收敛速度.
1 建立算法模型
1.1 终端区环境
由于机场附近的航线非常复杂,飞机在此空域活动频繁,因此需要设立终端管制区进行合理管制. 飞机的起飞和降落都将在该区域接受管制员的调度,安全、有序的完成离场和进场. 终端区结构如图1所示.
终端区的定义和作用使其成为了极其复杂的区域,也是造成空中交通拥堵的关键因素. 仅仅依靠新建跑道或扩大终端区等改善硬件条件的方法已经不足以解决终端区空中交通压力过载的问题. 采取更有效的利用已有的资源、选择合理的飞机降落次序、提高跑道容量等策略,可以大大缓解终端区和机场拥堵带来的交通压力.
本文将针对飞机进场排序问题,并基于已有的算法,提出一些改进和创新,力求得到一个更加高效的问题解决方案.
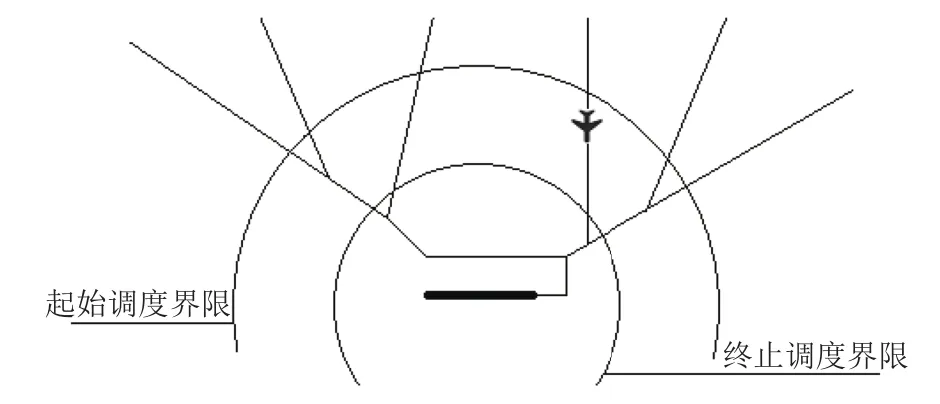
图1 终端区结构示意图
1.2 算法模型
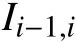
由国际民航组织规定的不同机型之间的最小尾流时间间隔标准(单位: 秒)如表1所示.
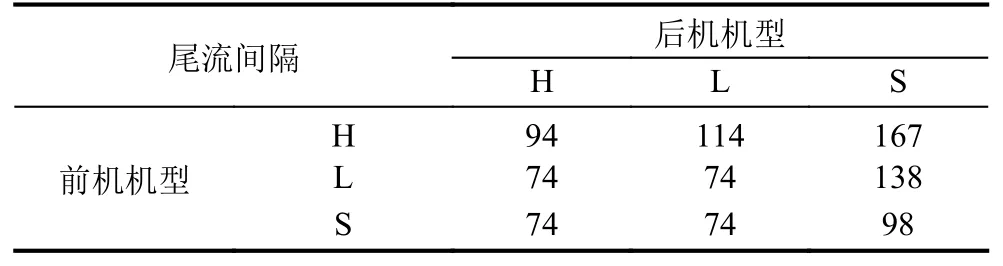
表1 尾流间隔标准
模型约束条件:
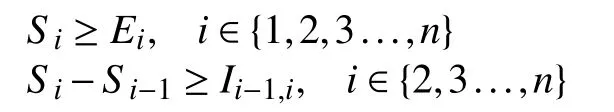
前者表示每架飞机实际降落时间不得早于预计降落时间; 后者表示相邻飞机实际降落时间间隔不得小于尾流时间间隔要求. 根据上述约束条件,第i架飞机的实际降落时间应为:
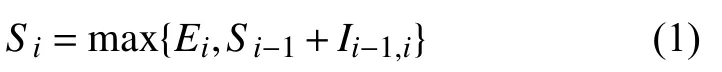
第i架飞机的延误时长为:

对于单架飞机来说,延误代价主要是由飞机类型、等待时长和航班优先级这些因素决定. 参考文献[8,9]并加以改进得代价系数公式:
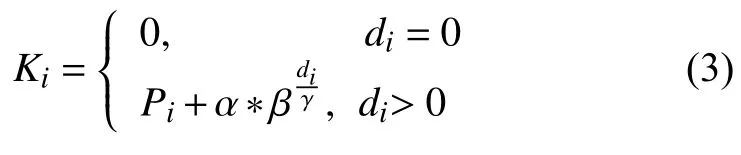
公式 (3)参数说明: Pi表示飞机 i的优先级,用于调整特定航班降落优先级或应对紧急处理.α,β,γ均为正整数,其中,α 为与机型相关的线性参数,β 为与机型相关的指数底数,γ为时间延误基数. 代价系数的含义:即飞机在延误时长di达到γ后,该飞机的延误代价系数会根据不同机型决定的α、β以及di的大小呈指数增长,若 di=0,则 Ki=0,延误代价也等于 0.
根据上述条件,每架飞机的延误代价可如下计算:
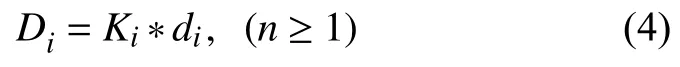
为避免出现延误代价集中在个别飞机上,采用各架飞机延误代价平方和建立模型:
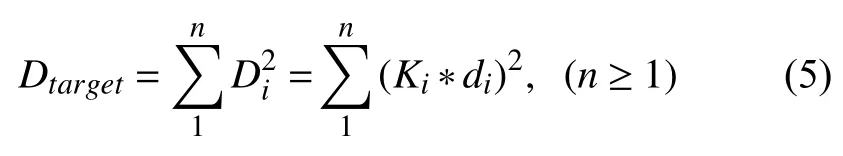
那么,问题转化为求得飞机使Dtarget的值最小的飞机队列. 个体适应度函数:

2 改进的遗传算法
2.1 改进遗传算法概述
为加快遗传算法的收敛速度,文献[10]中提出了交叉掩码的概念和使用,以此来保证交叉、变异得到的后代染色体会继承父代的优质基因,提高个体适应度,从而加快收敛. 然而,交叉掩码的使用可以保护高适应度染色体,但也会阻碍低适应度染色体的进化,延缓整个种群的进化速度. 尤其是在搜索初期,如果较优质染色体仅占很小的比例,那么搜索周期可能会被大幅延长.
为了既能利用交叉掩码带来的优势,又不阻碍低适应度染色体的进化,可以尝试针对不同适应度的染色体采用不同的交叉算子和变异算子做区别处理. 对高适应度的染色体,通过使用交叉掩码提供保护; 对低适应度染色体,采用部分映射杂交算子(Partially mapped crossover,PMX)完成交叉操作. 通过这种双交叉算子的遗传算法来提高种群收敛速度,从而更快的得出可行解.
2.2 编码
为方便后文中将介绍的重排算子的使用,飞机i的编码采用“飞机型号”+“该飞机在同类型飞机中预计到达跑道先后的序号”,不同类型飞机编码互不影响. 编码结果举例: S1、L1、S2、H1、S3、S4、H2、S5、L2、S6. 该编码方式可以保证在交叉、变异或重排后,每架飞机编号依然唯一,符合实际意义.
2.3 自适应算法
自适应遗传算法是针对每个染色体的适应度来计算适合该染色体的Pc和Pm. 对高适应度的染色体降低Pc和Pm,使其得到保护; 反之,对适应度较低的染色体提高Pc和Pm,使其在下一代中被淘汰. 目的是避免发散和陷入局部最小[11]. 自适应遗传算法的作用与本文的目的一致. 因此,算法将采用以下公式计算Pc和Pm[12]:
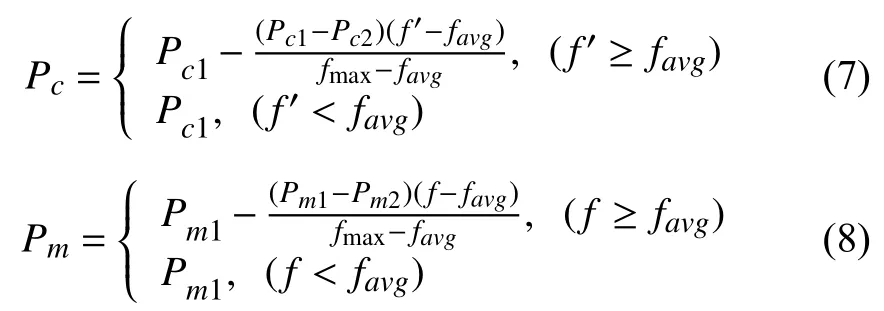
式中,f为适应度值,f’取双亲染色体的适应度中的较大值,fmax表示当代种群中的适应度最大值,favg表示当代适应度平均值. 一般Pc1和Pc2分别取0.9和0.6,Pm1和Pm2分别取0.1和0.001.
2.4 双交叉算子
2.4.1 交叉掩码
交叉掩码的计算[10]: 交叉掩码是根据近两代的适应度最高的个体的相似基因来确定的. 取近两代适应度最高个体的染色体进行比较,对应基因座的基因相同,则交叉掩码对应位置记为1,否则记为0,如此就产生了交叉掩码,并可以利用它将优质基因传递下去.
具体的,在本算法中计算示例如下.
已知i-2、i-1代种群中适应度最高的染色体Ci-2、Ci-1,则第i代交叉掩码的计算如下:
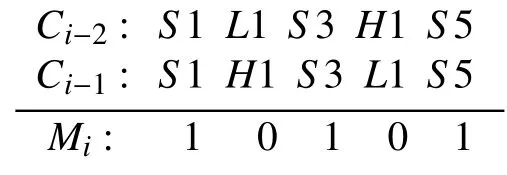
在染色体使用交叉掩码进行交叉操作时,交叉掩码基因为1的基因座直接沿用父代基因,剩余基因按照另一条父代染色体中相应基因的顺序进行排序. 在本算法中示例如下:
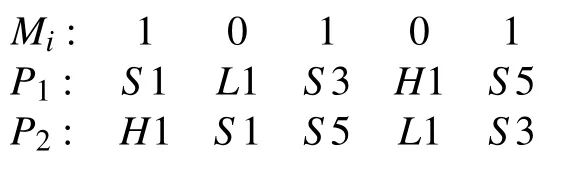
那么得到的孩子染色体如下(假设两条染色体适应度均符合用交叉掩码进行交叉操作):

使用交叉掩码进行交叉操作的优势在于父代的优质基因完全得以保留,使高适应度个体平稳进化,避免发散.
2.4.2 部分映射杂交算子[13]
第一步. 在范围[1,n)(n为飞机数量)随机产生两个整数r1、r2,将待交叉染色体均分为3段,并交换中间部分. 例如:r1=2,r2=5.
交叉双亲初始状态:

交换中间部分得:

第二步. 染色体两端部分有与中间部分重复的基因用*代替,表示冲突基因. 即:


该算子的优势是交叉过后,后代的染色体仍具有每个基因不会重复的特点,符合飞机队列的实际意义.并且,后代将部分保留父代的飞机序列,也达到了进化的目的.
2.4.3 双交叉算子
如上所述,交叉掩码具有保护优质染色体的能力,但也有阻碍劣质染色体进化的弊端. 因此,考虑使用双交叉算子来针对不同适应度染色体进行不同的交叉操作.
当选取的两条父染色体,一条为优质染色体,另一条为劣质染色体时,优质染色体使用交叉掩码进行交叉操作; 同时对两条父染色体进行部分映射杂交操作,产生的两个后代染色体选取适应度较高者保留.
2.5 变异算子
根据排序的实际意义,要求排序结果中包含所有飞机编码且每架飞机编码仅出现一次. 因此,变异算子采用染色体内部变异的方式,以满足上述要求. 并且考虑到重排算子的存在,则应随机选择型号不同(即编号字母不同)的两个基因进行交换.
变异操作示例如下:

随机选取产生变异基因为:S1,L1. 则变异操作后结果如下:

2.6 重排算子
重排算子参考了文献[14]中命题1提出的一条理论: 同类型的飞机,应按其预计到达跑道的时间先后依次着陆. 但该理论没有考虑航班优先级对降落次序产生的影响,需要在使用时做相应处理. 重排操作是在变异操作之后,其目的是使新生的飞机排序结果的适应度更高.
本文中的重排操作是指将变异操作后得到的飞机序列中的各类型(H,L,S)飞机分别按飞机的预计到达时间分别排序. 具有高优先级的飞机不参与这次排序,防止高优先级飞机被延后.
具体的在本算法中使用重排算子的示例如下:

对C进行重排操作后得:
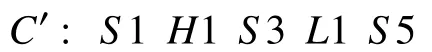
2.7 改进遗传算法流程
第一步. 获取待排序航班信息,为飞机编码;
第二步. 随机产生初始种群(染色体数量根据飞机数量决定,可取与飞机数量相等的值);
第三步. 计算个体适应度值,判断是否符合要求.符合要求,则输出结果; 否则进入下一步;
第四步. 根据前两代最优适应度染色体计算交叉掩码(从第三代开始);
第五步. 采用赌轮盘选择法从当代种群中选出双亲;
第六步. 采用自适应算法公式(7)计算Pc,根据双亲的适应度选择对应交叉方式进行交叉操作;
第七步. 采用自适应算法公式(8)计算Pm,进行变异操作;
第八步. 对染色体进行重排操作,产生新个体;
第九步. 新生代是否达到种群数量要求,未达要求返回第五步继续产生后代; 否则,返回第三步循环寻优.
3 实验仿真及分析
本实验采用C++编写算法仿真程序,对10架次飞机在单跑道降落的情况进行模拟,分别使用先到先服务算法和双交叉算子遗传算法对飞机待降队列进行排序,计算两种排序结果的总延误代价及个飞机延误代价平方和用作排序结果对比; 记录遗传算法种群适应度变化情况,检验收敛速度是否达到预期目标.
算法参数说明: 已知飞机的预计到达时间、飞机类型; 飞机类型为H、S、L的飞机,α分别取 20、15、10,β=2,γ=600,即飞机在延误 10 分钟以上,延误代价将呈指数增长,且重型飞机延误代价系数底数是轻型飞机的2倍,中型飞机延误代价系数底数是轻型飞机的1.5倍; 种群初始数量取20,最大遗传代数取100,初始两代交叉掩码无法计算,均取1; 自适应算法中Pc1、Pc2分别取 0.9和 0.6,Pm1、Pm2分别取 0.1和0.001. 使用以上参数进行仿真,得到的结果如表2、表3所示.

表2 FCFS 排序结果

表3 改进遗传算法排序结果
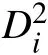
各飞机延误代价平方和变化曲线如图2所示. 种群在前10代收敛速度很快,在第10-50代进化更加平稳,在第50代左右达到稳定,与文献[10]中的收敛曲线对比,收敛曲线相似,但平均提前 5 代达到稳定,基本达到算法改进预期目的.
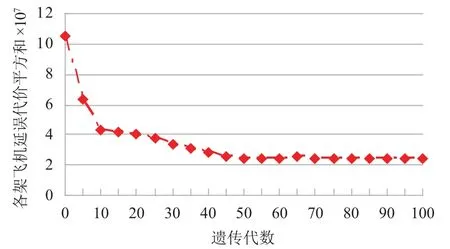
图2 延误代价平方和曲线图
4 结束语
本文针对终端区飞机排序问题,结合文献[10]提到的交叉掩码的使用方式,再融入使用双交叉算子针对不同适应度染色体进行不同交叉操作的思想,提出了一种改进的遗传算法. 根据实验数据,证明该算法的收敛速度相比文献[10]中的算法有进一步的改进,得到的排序结果也达到了降低航班延误总代价的效果,且延误代价分配更加均匀.
1Venkatakrishnan CS,Barnett A,Odoni AR. Landings at Logan airport: Describing and increasing airport capacity.Transportation Science,1993,27(3): 211–227. [doi: 10.1287/trsc.27.3.211]
2王莉莉,史忠科,张兆宁. 机场着陆排序的一种滑动窗优化算法. 中国民航学院学报,2004,22(6): 18–21.
3Neuman F,Erzberger H. Analysis of sequencing and scheduling methods for arrival traffic. NASA-TM-102795,1990.
4Erzberger H,Nedell W. Design of automated system for management of arrival traffic. NASA TM 102201,1989.
5Neuman F,Erzberger H. Analysis of delay reducing and fuel saving sequencing and spacing algorithms for arrival traffic.NASA TM 103880,1991.
6Holland JH. Adaptation in Natural and Artificial Systems.Ann ArborMI: The University of Michigan Press,1975.
7常会贤,曲仕茹. 终端区航班排序的遗传算法. 测控技术,2010,29(7): 91–93,101.
8白重阳,张学军,管祥民. 基于改进遗传算法的终端区排序研究. 航空计算技术,2011,41(5): 42–44,48.
9陈亮,邹赟波,吴值民. 改进遗传算法在终端区飞机排序中的应用. 军事交通学院学报,2013,15(1): 29–33.
10张维杰,龙华,胡婷,等. 改进的遗传算法在延误飞机进场排序中的应用. 信息技术,2016,(7): 78–83.
11陈长征,王楠. 遗传算法中交叉和变异概率选择的自适应方法及作用机理. 控制理论与应用,2002,19(1): 41–43.
12焦潇冰,费向东,谢泽辉. 基于改进的遗传算法航班进港排序模型研究. 计算机技术与发展,2014,24(2): 246–249.
13张泳,赵建民,朱信忠,等. 基于 SLP 方法的遗传算法在多目标布置设计中的应用. 计算机时代,2010,(5): 1–3,7.
14孟祥伟,张平,李春锦. 到场飞机排序及调度问题的Memetic 算法. 西南交通大学学报,2011,46(3): 488–493.
Application of Double Crossover Operator Genetic Algorithm to Aircraft Sequencing in Terminal Area
ZHAO Yan1,YUE Jun2,LIU Dan1
1(Research Institute of Electronic Science and Technology,University of Electronic Science and Technology of China,Chengdu 611731,China)
2(Research Institute of Southwest Electronic Telecommunication Technology,Chengdu 610041,China)
Nowadays,the widespread phenomenon of flight delays does not only increase massive flight costs,but also impacts the experience of passengers. Reasonably adjusting the aircraft queue in terminal areas can raise the utilization ratio of the runway and reduce flight delays. Finally,the cost of delay can be cut down. To resolve the problem of aircraft scheduling in terminal areas,this article puts forward an genetic algorithm including double crossing operator. Different crossover operations are carried out for chromosomes with different fitness so that the quality of chromosomes can be protected and the others continue to evolve. At the same time,reordering operator is introduced to optimize the descendants after mutation to improve convergence rate of genetic algorithm and makes it more suitable for practical use.The experimental results show that the convergence rate of algorithm is improved and the feasible solution can be obtained within acceptable time.
air traffic control; terminal area; aircraft sequencing; genetic algorithm; crossover operator
赵俨,乐俊,刘丹.双交叉算子遗传算法在终端区飞机排序中的应用.计算机系统应用,2017,26(12):110–115. http://www.c-sa.org.cn/1003-3254/6070.html
2017-03-06; 修改时间: 2017-03-23; 采用时间: 2017-03-27
