基于模糊核优化的图像盲去模糊算法

尤佳旗

(上海理工大学 机械工程学院，上海 200093)

基于模糊核优化的图像盲去模糊算法

尤佳旗

(上海理工大学 机械工程学院，上海 200093)

针对图像的模糊算法优化问题，首先选取高斯分布拟合自然图像的分布特性，利用双边滤波器从模糊图像中提取出清晰的图像边缘。针对降噪进行参数设置，在初步估计出模糊核之后，对模糊核进行正规化修正工作。最后在图像复原阶段，利用优化的凸函数拟合自然图像分布，并利用快速傅里叶变换提高算法计算速度。实验结果，表明该模糊核优化算法与现有的其他算法相比,复原后的图像具有更好的视觉效果,且计算时间减少约20%。

高斯分布；滤波器；模糊核；傅里叶变换

图像的运动模糊是指相机在曝光时间范围之内产生移动从而导致的图像重影的现象，这种重影现象在视觉上呈现为图像的模糊感。盲去模糊是指在模糊方式未知的情况下，仅仅依靠退化图像本身来还原出原始清晰图像的过程，图像的运动模糊过程可以通过将清晰图像同模糊核(PSF:即点扩散函数)卷积来完成，然后加上噪声因素的考虑,公式如下

B=K*L+N

(1)

其中，“*”表示二维卷积操作；L表示原始清晰图像；B表示退化的模糊图像；K表示模糊卷积核；N表示加性噪声。式(1)适用于相机沿着平行于图像平面的方向移动的情况。

近年来的盲去模糊算法取得了较多的进展。绝大多数方法依赖于图像的先验分布状况对清晰图像或者模糊核进行估计。文献[1]中使用零均值高斯混合分布来匹配具有重尾分布的图像先验模型，然后使用变分贝叶斯框架进行估计。文献[2]中利用稀疏先验分布同时描述原有清晰图像和模糊核，然后使用一种交替极小化的方式进行优化。文献[3]中通过首先定位阶梯状边缘然后将局部强度朝着边缘传播的方法来预测清晰的图像边缘。文献[4]中使用双边滤波和冲击滤波来预测清晰的边缘。文献[5]采用超拉普拉斯分布来建模，因为它比标准拉普拉斯分布更接近于重尾分布并且采用一个有效的最小化方法来解决这个非凸优化问题。

在一般的去模糊算法中,先进行模糊核估计,然后通过去模糊算法对图像进行图像复原。得到精确模糊核的步骤为：增强并选择有用的图像边缘；利用提取的图像边缘估计模糊核；对得到的模糊核进行修正。由于盲去运动模糊过程对噪声极其敏感,即使很小的噪声也会严重影响图像复原的效果。因此,得到精确的模糊核来估计出清晰的图像的两个前提是：恢复突出的边缘和噪声抑制。本文就通过对这两个方面进行改进得到一种新的图像去模糊算法。

1 边缘提取

由于图像复原过程对噪声极其敏感,即使很小的噪声也会严重降低图像复原的效果。传统的滤除噪声的方法是使用高斯滤波器,计算目标像素点邻域内所有像素值的权重平均值,其中距离邻域中心越远,权重越小。这种方法虽然能在保留图像信息的同时消减噪声,但会使图像中细小边缘模糊,这样将不利于用图像边缘估计模糊核。本文利用双边滤波器[6]对模糊图像进行平滑操作,能在降低图像噪声的同时保持图像边缘。双边滤波器公式为

(2)

其中，Ix表示双边滤波器处理输出结果;k为归一化因子;L表示模糊图像;x表示目标像素点，是以x为中心的邻域;"ξ" 表示邻域像素点;f函数表示x与"ξ" 两个像素之间的空间距离;g函数表示像素值之间的相似程度权重。

为了利用图像边缘估计模糊核，需要对增强的图像边缘进行提取。而双边滤波器只能起到滤除噪声和保持边缘的作用,并不能使图像的边缘信息增强。因此本文采用改进的冲击滤波器对模糊图像进行边缘增强,使冲击滤波器具备降噪和边缘增强的同时,还能保持图像总变分不变,信号能量不会随着时间流逝而被削弱。首先,Osher和Rudin[7]提出一种双曲线偏微分方程图像锐化增强模型,即冲击滤波器的原型。其数学模型如下

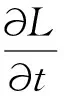
(3)

要增强图像对噪声的抗干扰能力,通常做法就是卷积信号的二阶导数和低通滤波器,比如高斯滤波器,其数学公式为

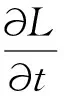
(4)

其中，Gσ是标准偏差为σ的高斯分布。该冲击滤波器的缺点是：当模糊核过小时，无法良好的过滤噪声；而当模糊核过大时，虽然噪声能被过滤，但信号精度却大幅下降。Guy Gilboa针对该问题做出如下的改进，使其能够正确处理有噪声的信号[8]。首先在原有冲击滤波器模型中增加一个线性扩散项，目的是降低放大过程引入的噪声干扰，其数学模型为

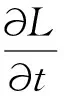
(5)

其中，λ>0，用于调节冲击滤波和扩散的权重。通过让扩散项ΔL乘以‖sign(L)‖可以使总变分差[9]保持不变，当图像梯度L≠0时，‖sign(L)‖=1，即信号不平坦时，对图像进行冲击滤波。当图像梯度L=0时，‖sign(L)‖=0 ，即不破坏信号的平坦区域。因此该模型具备降噪以及边缘增强的功能的同时，能保持模糊图像总变分不变,使信号能够不会随着时间流逝而被削弱。

文献[10]提出结合时间因素来达到降低噪声和边缘增强的目的,改进的冲击滤波器为

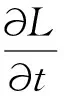
(6)

该方法用arctan(α·ΔL)代替sign(L)，使函数具备控制冲击方向的能力，也能控制边缘的锋利程度以及收敛速度。参数a越大，边缘就越锋利。越接近拐点，其ΔL越大，靠近边缘比相对平缓点的区域就能更快变得锋利。在处理初始阶段，信号所含的噪声比较强烈，这时图像梯度估计存在较大的误差。此时通常需要一个降噪过程，因此通过结合时间因素可以达到降噪与边缘增强的目的。在处理初期该滤波器主要表现为降噪能力(因为此时时间较小，冲击滤波器的能力被大幅削弱)，随着时间的流逝，冲击滤波器的权重逐渐增大，最终达到增强图像边缘的目的[11]。

2 边缘选择

当模糊核尺度过大时，图像中某些突出边缘会不利于模糊核估计，因此要选取有用的边缘来进行模糊核估计是非常重要的。参照文献[12]设置选取准则，公式如下

(7)

其中，B表示模糊图像；Nh(x)以像素x为中心的h×h的窗口；0.5是避免在平坦区域产生较大r值。B是梯度,因此在平坦位置,B(y)值很小。在尖峰位置,B(y)值有正有负,在计算公式的分子部分时,值会有较大抵消是在Nh(x)的绝对峰值幅度总和。因此,r值较小时代表此处是平坦区域或者尖峰。

为了去掉图像中的噪声,本文利用模型M设置阈值去除较小的r值。

M=H(r-τr)

(8)

其中,H(·)是阶跃函数，τr是阈值。最终选择的图像边缘为

LS=

(9)

3 快速模糊核估计

B=K*Ls+N

(10)

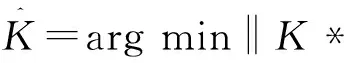
(11)

由于目标函数中的变量都是矩阵,所以可用如下方程式重新表达

f(K)=(K*Ls-B)T(K*Ls-B)+ηKTK

(12)

对式(9)两边求偏导，可得

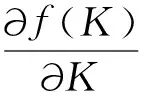
(13)

由式(13)可知，K有闭式解

(14)

运用快速傅里叶变化(FFT)技术，将矩阵的空间卷积运算转化到频率域的点乘运算,以此大幅降低计算量。

(15)

模糊核修正：

(1)模糊核的非负特性,将模糊核中过小的元素值以及负值剔除。定义模糊核的阈值Tk

(16)

其中，max(K)表示模糊核K中最大值；

(2)保持模糊核的连续性,排除分支,仅保留主要结构；

(3)根掘模糊核的能量守恒特性,对模糊核进行归一化,即元素和等于1。

图1 模糊核的修正结果对比

4 快速图像反卷积

一般盲目反卷积就是交替优化模糊核K和清晰图像L，在模糊核估计和图像反卷积过程中，用以下方程求解[14]

K′=arg minK{‖B-K*L‖+ρK(K)}

(17)

L′=arg minL{‖B-K*L‖+ρL(L)}

(18)

其中，‖B-K*L‖是数据拟合项，通常使用L2范数；ρK(K)和ρL(L)分别是模糊核K和清晰图像L的泛函数，是正规化项。

当ρ=2时，表示该模型运用高斯分布先验知识，即约束最小二乘法，其优化函数定义为

L′=arg minL{‖K*L-B‖2+μ‖L‖2}

(19)

该优化函数是一个凸函数,因此,一定存在闭合解。运用拉格朗日算法最小化优化函数[15],其过程如下。

(1)由于该优化函数中的变量都是矩阵形式，可将其重写成

f(L)=(K*Ls-B)T(K*Ls-B)+
μ(L)T(L)

(20)

(2)对等式两边L求偏导数，得

(21)

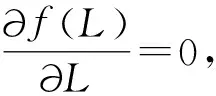
(22)

(4)运用快速傅里叶变换(FFT),将矩阵的空间域的卷积运算转化到频率域的点乘运算,可大大地降低计算量

(23)

为保持图像的清晰边缘，定义目标函数

L′=arg minL{‖l*k-B‖2+μ‖L-Ls‖2}

(24)

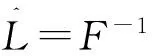
(25)

由于快速算法重点在于提高运算速度,对实际釆集到的运动模糊图像的处理结果不理想,因此对人工合成的运动模糊图像进行处理通过实验,对运动模糊图像进行复原。选取图像大小为256×256,首先添加运动方向为135°,运动长度为21的运动模糊核,再添加噪声是均值为0方差为0.1的高斯噪声。

图2 第1次估计

图3 第2次估计

图4 第3次估计

图5 复原效果

本文算法来用多尺度复原模糊核,然后用估计得模糊核复原出清晰图像,选取前3次变化叫明显的迭代。图2是第1次估计，图3是第2次估计，图4是第3次估计,得出清晰模糊核。最后,由估计得模糊核,反卷积出清晰图像,复原结果如图5所示。由图5复原结果与其他文献中含噪声的滤波器复原结果相比，算法的复原结果要好很多。从图像复原结果图可看出,图像的平滑区域复原效果理想,但在图像尖锐的边缘区域却仍然存在明显的振铃效应。

5 结束语

本文对图像盲去模糊技术进行了深入研究，涉及到快速盲去模糊算法、模糊核估计技术，提出了利用图像边缘及多尺度策略估计模糊核。实验结果表明，该算法与现有的其他算法相比，复原后的图像具有更好的视觉效果，且计算时间可减少约20%。

[1] Fergus R,Singh B,Hertzmann A,et al.Removing camera shake from a single photograph[J].ACM Transactions on Graphics,2006,25( 3):787-794.

[2] Shan Q,Jiaya J,Agarwala A.High quality motion deblurring from a single image[J].ACM Transactions on Graphics,2008,27(3):73-76.

[3] Joshi N,Szeliski R,Kriegman D J.PSF estimation using sharp edge prediction[C].Piscataway,NJ,USA:IEEE Conference on Computer Vision and Pattern Recognition,2008.

[4] Cho S,Lee S.Fast motion deblurring[J].ACM Transactions on Graphics,2009,28(5):145-149.

[5] Krishnan D,Fergus R.Fastimage deconvolution using hyper-laplacian[C]. NJ,USA: Proceedings of Neural Information Processing Systems Blurred Lut Nr，2009.

[6] Tomasi C,Manduchi R.Bilateral filtering for gray and color images[J]. IEEE Computer Society, 1998,15(8):839-848.

[7] Osher S,Rudin L.Feature oriented image enhancement using shock filters[J].SIAM Journal on Numerical Analysis, 1990,27(4):919-940.

[8] Gilboa G,Sochen N,Zeevi Y Y.Regularized shock filters and complex diffusion[J].Springer,2002，54(8):399-413.

[9] Tony F Chan, Chiu Kwong Wong. Total Variation blind deconvolution[J].IEEE Transactions on Image Processing,1998,7(3):370-375.

[10] 李信一.单帧运动模糊图像复原问题的研究[D].南京:南京航空航天大学,2013.

[11] 田冰.线阵干涉仪解模糊算法研究[J].电子科技，2016,29(8):114-116.

[12] Richardson W,Bayesian H.Based iterative method of image restoration[J].Jouranal of the Optical Society of Ameirca,1972,62(1):55-59.

[13] Cho S,Lee S.Fast motion deblurring[J].ACM Transactions on Graphics,2009,28(5): 145-152.

[14] Hurley N,Rickard S.Comparing measures of sparsity[J].IEEE Transactions on Information Theory,2009,55(10):4723-4741．

[15] 刘梦娇.基于直方图的图像模糊聚类分割算法[J].电子科技,2016,29(11):107-111.

Blind Image Deblurring Based on Optimized Fuzzy Kernel

YOU Jiaqi

(School of Mechanical Engineering, University of Shanghai for Science and Technology,Shanghai 200093,China)

In view of optimizing image fuzzy algorithm，distribution characteristics of natural images is fitted by selecting gaussian distribution firstly. The bilateral filter is used to extract image edges from blurred image. Setting parameter for noise reduction, after preliminary estimate the fuzzy kernel, fuzzy kernel revision is normalized. Finally, in image restoration stage, optimized convex function is used to fit distribution of natural images and fast Fourier transform algorithm are used to improve calculation speed. The experimental results show that compared with other existing algorithms, this image fuzzy optimization algorithm has better visual effect and significantly reducing computing time about 20% after recovery.

gaussian distribution;filter;fuzzy kernel;the Fourier transform

2017- 02- 28

国家自然科学基金 (51475310)；教育部高等学校博士学科点专项科研基金(20133120120005)

尤佳旗(1992-)，男，硕士研究生。研究方向：图像处理。

TP18

A

1007-7820(2018)01-054-05