多无人机协同任务规划

夏令儒，孙首群

(上海理工大学 机械工程学院，上海 200082)

多无人机协同任务规划

夏令儒，孙首群

(上海理工大学 机械工程学院，上海 200082)

为解决多无人机协同规划军事目标打击的问题，基于多旅行商(TSP)数字规划理论进行路径和时间的优化。文中建立了多旅行商(TSP)数字规划模型，并根据任务性能和区域划分理论，利用退火算法求解出该模型的最优解。使用A*路径规划算法，通过编程仿真规划出了无人机的时间最优路径。结果表明，该方法较好地解决了当前无人机协同作战的目标分配问题，大幅提高了无人机协同作战的能力。

多无人机；模拟退火算法；A*算法；最优路径规划；协同作战

无人机是一种具备自主飞行和独立执行任务能力的新型作战平台，不仅能够执行军事侦察、监视、搜索以及目标指向等非攻击性任务，而且还能够执行对地攻击和目标轰炸等作战任务[1]。而实现无人机协同作战的自主控制，需要首先解决目标威胁实时评估、任务目标分配和攻击排序，针对不同问题提出的多任务需求, 确定出各无人机的任务顺序, 包括执行任务的方式、执行任务的类型以及不同任务的执行顺序和时间等, 以确保多无人机在多任务执行过程中的协同性。用最优化的方法研究高效率协同多任务分配方法是提升无人机未来战场适应能力和作战效能的重要途径, 具有较大的理论和合效应及系统动力学。

实际意义。目前，常用的目标分配方法有：自主优先权的分配和协同优先权的分配[2-5]，这些目标分配方法考虑的对象都是空中目标。在目标分配时，在考虑敌机对我方无人机威胁的同时，增加了地面目标的威胁，进行无人机协同作战的目标分配。

基于多边形区域分割的基本思想，将多UAV 协同作战分解为区域问题，然后分别优化求解。在满足约束条件下，达到区域与整体的最优解，根据无人机性能评估结果，最后通过仿真实验显示了所给方法的有效性。

1 无人机群协同作战模型建立

问题描述

假定现有P01、P02、P03、P04、P05、P06、P07具有FY-1、FY-2、两种不同配置无人机的基地，要对10个目标基地共68个目标进行侦察和军事打击，寻找出最优的解决方法。

约束条件

(1)FY-1型无人机主要担任目标侦察和目标指示，巡航飞行速度为200 km/h，最长巡航时间为10 h，巡航飞行高度为1 500 m；

(2)FY-1型无人机每次只能携带S-1、S-2其中一种装备；

(3)S-1、S-2两种不同载荷对于每个目标群各自至少侦察一次；

(4)FY-2型无人机主要担任通信中继，巡航飞行速度为300 km/h，最长巡航时间为8 h，巡航飞行高度为5 000 m；

(5)无人机的最小转弯半径为70 m；

(6)同一基地的两架无人机起飞时间间隔和降落回收的时间间隔不低于3 min；

从连接度看：连接度为与某一空间直接相连的空间数目，连接度高的空间能方便到达多个相邻空间。轴线分析地图表明，余荫山房中部的“烷红跨绿桥”区域空间连接度较高，穿过性交通较大，与“深柳堂”前庭、旱庭、“临池别馆”前廊等空间直接相通，使用者可以很方便地在园中的不同区域穿行[13]。相反，余荫山房西部与南部区域空间的连接度较低，使用者行至这一区域没有太多的选择，只能按照设计好的路线游览。对于连接度只有1的“深柳堂”东侧厢房来说，穿过性交通较少只与一个空间直接相连，较为僻静。

(7)无人机执行完任务后需返回原基地；

(8)每个目标群均配属雷达，且对FY型无人机的有效探测距离为70 km。

1.1 协同作战路线优化模型

基于侦察任务与路线长度之间的近似线性关系[6-7], 侦察路线优化模型通常以侦察总时间最短作为优化目标。通过分析侦察系统的特点, 可将侦察路线优化模型描述为基地为单位的各个雷达监测内部的目标点设计最短耗时的侦查路线，一方面起到降维的目的，另一方面估计出在每个基地的最短逗留时间。第二步是把以基地为单位的侦察时间串联起来，建立规划模型来计算要遍历这些基地总的侦察时间，估算出需要派出几架无人机出动侦查。思路流程如图1所示。

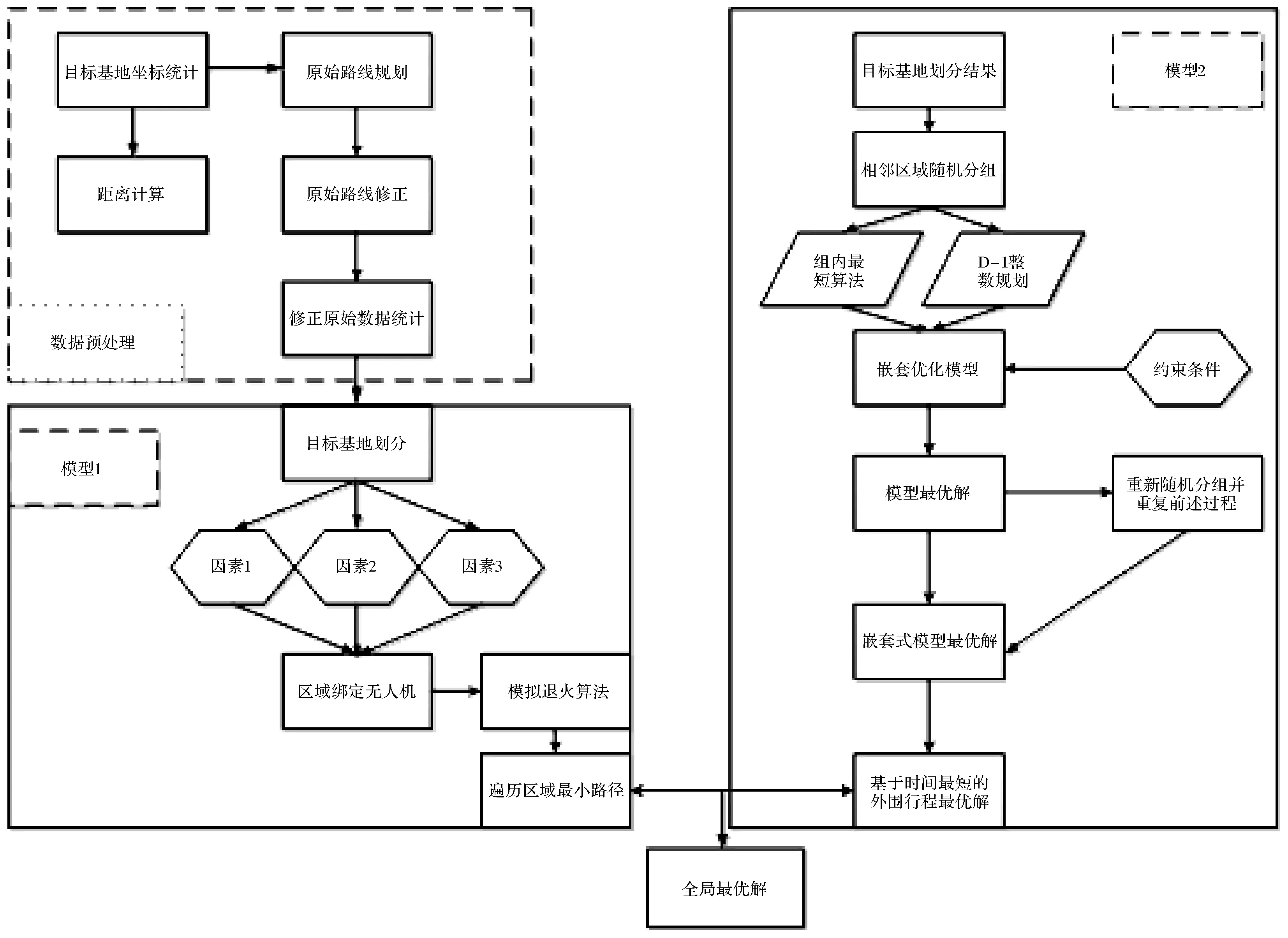
图1 思路流程图

1.2 无人机的任务分配

模拟退火算法[8]是所谓3大非经典算法之一，它脱胎于自然界的物理过程，与优化问题相结合。其思想源于固体的退火过程，即将固体加热至足够高的温度，再缓慢冷却。为寻找出最优解，把多无人机的协同任务数据用在退火程序中。

对任意基地内部，可以建立经典TSP规划模型[9]来求解最短时间的滞留路径。为简化计算，可以先不考虑无人机转弯半径70 m的限制。根据题设条件，假设无人机的任务分配原理如图2所示。

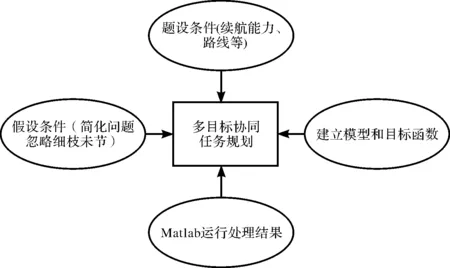
图2 无人机的任务分配原理

1.3 数学模型的建立

为了更加精确的解决无人机群协同作战问题，需要建立理论数学模型如下

Tmin=Ts1+Ts2

(1)

(2)

Ts2=(i=0,1,2,…,10)

(3)

(4)

(5)

其中，Ts1为s1和s2在雷达区分别的滞留时间；Tmin为s1和s2的最小滞留时间之和；Vk为s1和s2的平稳运行的速度(k=0,k=1)；r为雷达的辐射范围；Ts1Ai为s1在Ai号基地的滞留时间；sj为出目标群时的距离。

基于10个基地的建模并且运用Matlab运行处每个目标群最优路径所需的最短时间如表1所示 。

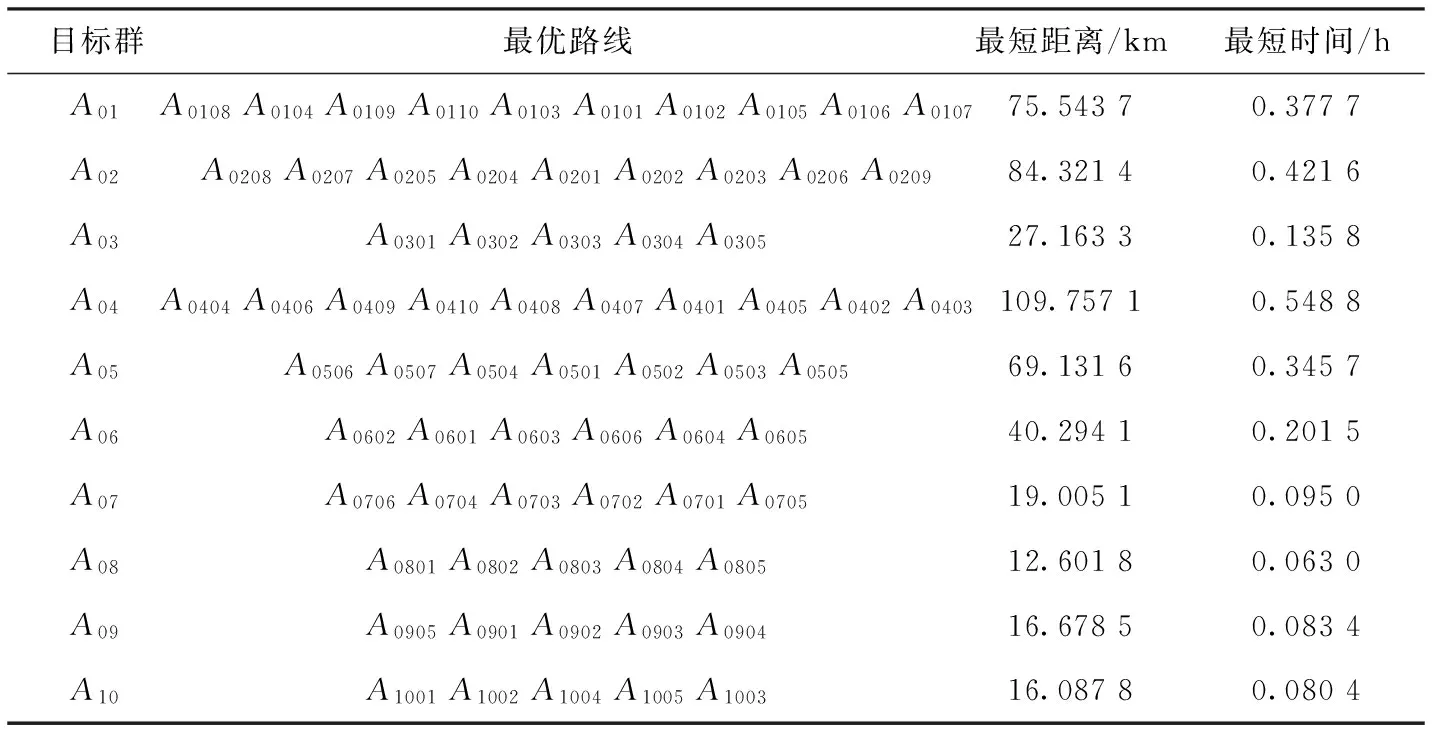
表1 每个目标群中最优路径及时间

2 A*路径规划算法及仿真

2.1 A*算法的选择

A*算法是一种经典的启发式搜索算法，一种静态路网中求解最短路径最有效的直接搜索方法，也是解决许多搜索问题的有效算法[11-12]。算法的创新之处在于探索下一个结点时引入了已知的路网信息 ，特别是目标点信息，增加当前结点有效评估，即增加约束条件，作为评价该结点处于最优路线上可能性的量度，因此首先搜索可能性较大的结点，从而减少探索结点个数，提高算法效率。

设O点为搜索过程中的某个节点， 它可以有 8 个扩展方向。首先建立二维平面的无人机运动，如下

(6)

(7)

式中，x和y为无人机在二维平面内的惯性坐标；v为无人机速度；θ为偏航角。

假设有n架无人机，定义第i架无人机的代价函数为

f(i)=g(i)+h(i),i=1,2,…,n

(8)

(9)

(10)

其中，(xi,yi)为第i架无人机的位置坐标；(xi1,yi1)是为i架无人机的待飞点；(xt,yt)为目标点坐标。由此设定为目标函数，编写成为Matlab程序。

2.2 约束条件

假设各无人机类型相同，时间步长为T,飞行速度为200 m/h, A*算法步长为 时，可以得到各无人机在A*算法不同步长下到达目标的时间集St1，St2，St3，…，求取它们的交集Ø=St1∩Si2∩Si3∩……。从Ø中选取最小的时间作为多无人机最优协同飞行时间t，使各无人机按照在t约束下的时间飞行，且各无人机同时到达目标点。即在最优协同时间t之后，X1=X2,Y1=Y2。

在无人机协同飞行过程中，当两架无人机之间的距离大于或等于无人机最大通信距离dmax时，启动通信距离限制约束。两架无人机在遵循小转弯半径约束的前提下，向减小两机距离的方向各运动一个步长。取各无人机当前位置为A*算法新的起始节点，重新规划协同航路。如果两架无人机在相互接近时又遇到威胁区域，此时为了保证无人机的安全，无人机应首先绕开威胁区域，然后再相接近，使相互间距离保持在通信距离范围内，具体流程如图3所示。

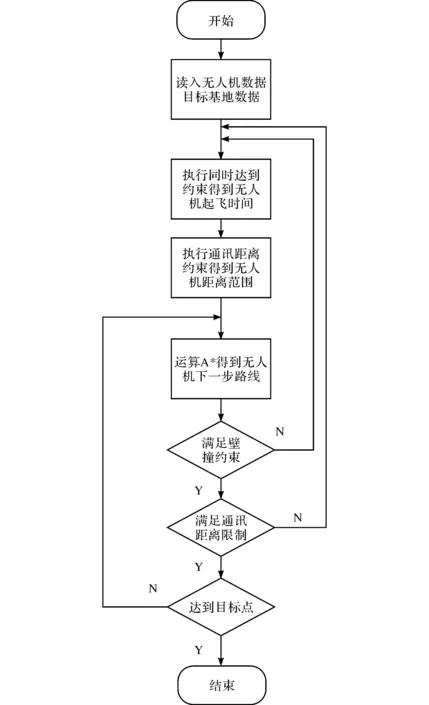
图3 A *算法流程图

2.3 仿真结果分析

区域A下FY-1型无人机的起始位置基地P01坐标为(368，319)，起始时刻t0为8:00，所要到达的目标基地的坐标为A010(264，715),且无人机的航速为v=200 m/s。

区域B下FY-2型无人机的起始位置基地的坐标为P07(360，110)，起始时刻t0为8:00，所要到达的目标基地A0501的坐标为(120，400)，且FY-2型无人机的航速为v=300 m/s。

将相邻两个点的位置相连，求出其距离，公式如下

(11)

(12)

则中间应规划航迹长度为dc=f0-c1-c2，接下来只要进行起始点为P01、目标点为A0101、 给定长为dc的定长航迹规划，多机协同航迹规划，在用A*算法实现定长航迹规划后，可进一步实现多人机协同航迹规划[14-15]。以 3 架无人机为例，其策略为：根据起始点、目标点以及途中要规避的威胁，3 架无人机先各自进行最短航迹规划，然后从中选取长度最大的一条作为参照，以其长度作为给定值，对其他两架无人机进行定长航迹规划。这样就实现了3机同时出发、同时到达且用时最短的协同航迹规划。

设在上述情形 1 下，第 1 架无人机的起始点P01坐标为(264，715)，目标基地坐标为(368，319)，第 2 架无人机的起始点P02坐标为(264，44)，目标基地坐标为A0501(120，400)，第 3 架无人机的起始点P03坐标为(392,220)，目标点A0701坐标为(10,451) 。设在上述情形2下，第 1 架无人机的起始点P05坐标为(392，275) ，目标点A0301坐标为(168，538)，第 2 架无人机的起始点P06坐标为(296，242)，目标点A0201坐标为(225，605)，第3架无人机的起始点P07坐标为(256,121)，目标点A0801坐标为(162，660)。

在Matlab环境下，进行上述单机定长航迹规划和3机协同航迹规划数字仿真。启发函数[16]取为当前节点到目标节点直线距离的1.4 倍。1.4 为启发系数， 决定了启发函数h(i)的大小。计算可得情形1下无人机应飞航迹的给定长度为f0=v(t1-t0)=470 km，情形 2 下无人机应飞航迹的给定长度为f0=v(t1-t0)=456 km，与问题飞航程470 km 非常接近，相对误差为 0. 383 6%。通过以上流程的建模和计算，代入N=3得到三架无人通讯机可以由最优路径进行保持通讯和侦查，由仿真结果图可以看出，本文设计的通信约束下的航路规划算法是合理和有效的。图4显示出FY-1型无人侦察机装载载荷在A01目标群中各目标间进行侦察的顺序及航线，10个目标群中整体路径规划如图5和路线分配图6所示。

图4 无人机在A01中侦察的顺序及航线

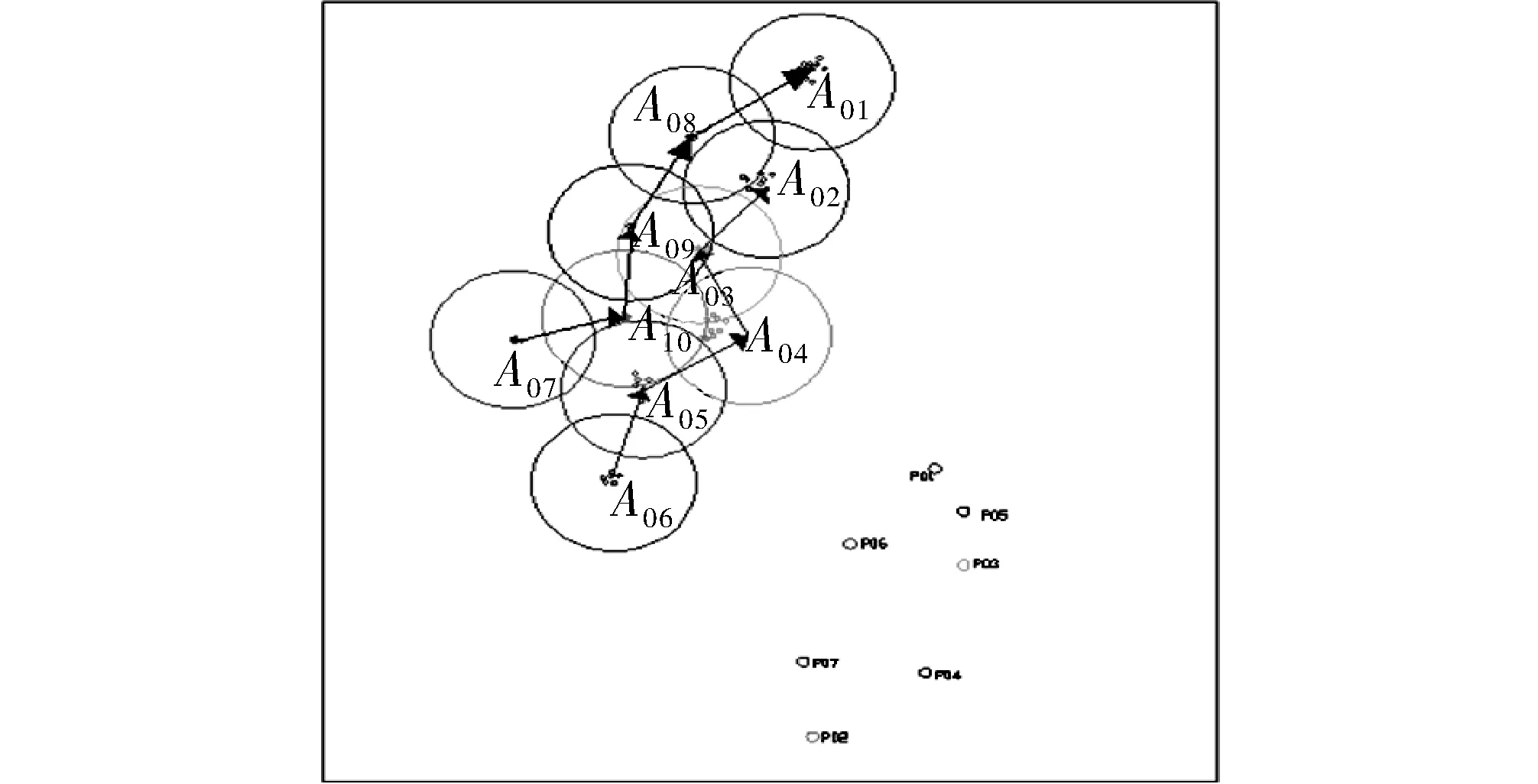
图5 整体路线规划

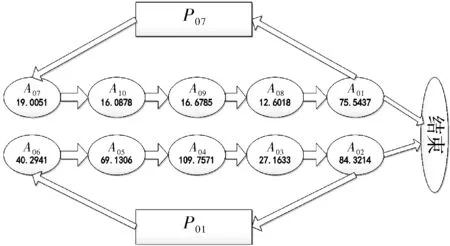
图6 整体路线分配图

3 结束语

(1)结合多目标、多无人机和多种作战任务的协同分配需求建立了数字规划模型，重点考虑了同一作战任务需要多架次无人机共同完成的情况，并结合协同任务的约束条件和协同任务的特点，构造了基于遗传算法的协同任务分配求解算法；(2)提出了改进的多无人机协同作战优化模型, 利用遗传算法得到侦察、打击目标与时间总和最短的优化路线改进模型,并解决多无人机多任务的优化问题；(3)将提出的路线优化问题的解决方案应用于实例, 运算结果证明该方法是适用和可行的。

[1] 杨俊超,史越,马海明.种人一自动系统协作的无人机航迹规划方法[J].计算机测量与控制,2015,23(9):25-31.

[2] 柏建普,吴强.蚁群混合遗传算法的研究及应用[J].电子科技,2011,24(4):20-23.

[3] 刘跃峰,张安.有人机/无人机编队协同任务分配方法[J].系统工程与电子技术,2010,32(3):584-588.

[4] 彭辉,沈林成,朱华勇.基于分布式模型预测控制的多UAV 协同区域搜索[J]. 航空学报,2010(3):594-600.

[5] Chen L D,Toru S.Data mining methods，applications and tools[J].Information System Management,2000,17(1):65-70.

[6] Szczerba R J.Robust algorithm for algorithm for real time route planning[J].IEEE Transaction on Aerospace and Electronic System,2000,36(3):869-878.

[7] 孟中杰,黄攀峰,闫杰.基于改进稀疏 A * 算法的高超声速飞行器航迹规划技术[J].西北工业大学学报,2010,28(2):182-186.

[8] 王丰雪,陈家琪.一种结合模拟退火和贪心策略的社团识别算法[J].电子科技,2016,29(2):8-10.

[9] 高海昌,冯博琴,朱利.智能优化算法求解 TSP 问题[J].控制与决策,2006,21(3):241-247.

[10] Brown D T.Routing unmanned aerial vehicles while considering general restricted operating zones[D].Ohio: Air Force Institute of Technology,2001.

[11] 郭文强,高晓光,任佳,等.基于图模型自主优化的多无人机多目标攻击[J].系统工程与电子技术,2010,32(3): 574-578.

[12] 高晖,陈欣,夏云程.无人机航路规划研究[J].南京航空航天大学学报,2001,33(2):135-138.

[13] 郭齐胜,郅志刚,杨瑞平,等.装备效能评估概论[M].北京:国防工业出版社,2013.

[14] 浦鹏,张金春,孙玺菁.多机协同多目标分配战术决策研究[J].战术导弹技术,2007,28(2):57-61.

[15] 荣少巍.基于改进A* 算法的水下航行器自主搜索航迹规划[J].电子科技,2015,28(4):17-19．

[16] 陈建荣,郭齐胜.无人机系统的系统效能评估[J].指挥控制与仿真,2008,33(5):45-48.

Planning Route for UAV Cooperative Combat

XIA Lingru，SUN Shouqun

(School of Mechanical Engineering，Shanghai University for Science and Technology，Shanghai 200000, China)

In order to solve the problem of multiple unmanned aerial vehicle cooperative planning military target attack, based on the theory of multiple traveling salesman (TSP) digital planning, path and the time of optimization. Multiple traveling salesman (TSP) was established by the digital planning model, and according to the theory of division and task performance, the annealing algorithm is used to derive the model of the optimal solution; Finally using the A * path planning algorithm, through the programming simulation time optimal path planning out of the unmanned aerial vehicle . Results show that the method solve the target assignment problem of unmanned aerial vehicle cooperative engagement, greatly improve the ability of the unmanned aerial vehicle cooperative engagement.

unmanned aerial vehicle;simulated annealing algorithm;A * algorithm;the optimal path planning;operation

2017- 03- 08

国家科技支撑计划项目(2015BAK16B04)

夏令儒(1990-)，男，硕士研究生。研究方向：大型油气管道泄露抢险密封技术。孙首群(1964-)，男，博士，副教授。研究方向：机电系统电热耦合效应及系统动力学。

TN256

A

1007-7820(2018)01-004-05