为什么时空变换必须是线性的
2018-01-06陈奎孚
陈奎孚
(中国农业大学理学院74#,北京 100083)
为什么时空变换必须是线性的
陈奎孚
(中国农业大学理学院74#,北京 100083)
尽管线性时空变换是狭义相对论的出发点,但至少从教学角度,对线性变换合理性的论证依然不清晰。笔者根据时空均匀性、时空各向同性和惯性系的等价性,严格地导出了时空的线性变换,其中关键概念是变换的时间缩放系数和空间缩放系数。沿此思路,进一步约束两个坐标系之间的时空缩放系数相等,并利用光速不变原理,导出了洛伦兹变换。
狭义相对论;洛伦兹变换;光速不变原理;惯性坐标系;惯性定律;匀速直线运动
很多教材在编写狭义相对论的洛伦兹变换这部分内容时,时空变换被默认成线性了。至于时空变换为什么必须是线性的,大多为泛泛论证。比如,有些教材说同一事件“在两个参考系中观察的结果必须是一一对应,这就要求变换关系呈线性”,然而(x′=x3,t′=t)也可以保证一一对应,但它显然不是线性的。爱因斯坦在最初那篇著名的狭义相对论论文是这样叙述的,“In the first place it is clear that the equations must belinearon account of the properties of homogeneity which we attribute to space and time”[1](原作为德文,本句英文来自GB Jeffery和W Perrett的1923年英文翻译版,中文翻译参见文献[2]),那爱因斯坦这句叙述是否又靠谱呢?
从另外一个角度,推演狭义相对论的洛伦兹变换究竟需要多少个假设呢?这个问题被很多人讨论过了[3],但至少从教学角度,分歧或模糊依然存在[4]。此外,狭义相对论适用于惯性系,但目前推导洛伦兹变换时,表面上并没有明确使用惯性系的性质。所谓的“在所有惯性系中,物理规律的表达形式都相同”的要求在哪个环节被使用了呢?本文的探究将表明上述问题的解答或多或少与时空变换的线性特性有关。
时空线性变换似乎是狭义相对论的“默认”,而前者被视为近代物理学的两大支柱之一(另一支柱是量子力学)[5],自然有科学家会审视支柱中“默认”的合理性。Lévy-Leblond曾经讨论过这个问题,但没有说清楚惯性系的贡献[6]。国内的冯胜奇也讨论过同一问题,但出发点与本文不同,结论自然也不同[7]。
“搜尽奇峰打草稿”是清代画家石涛在书画创作中极力主张的一种创作观点。他的书画作品之所以能有大成,也是因为他身体力行地推崇这句至理名言,所以才能把创作中的意境与灵感淋漓尽致地展现于他的作品当中。对于艺术他主张应该多搜集素材,多观察事物,手摹心记,在大自然当中不断地提炼自己的艺术表现手法,总结艺术规律,进而形成自己的艺术风格。以“搜尽奇峰”不辞辛劳的写生创作态度,从而在“打草稿”的过程中逐渐提炼自己的艺术语言,最终达到“外师造化,中得心源”的至高境界,也是石涛游历大江南北在奇峰怪石中“山川与予神遇而迹化”的悟道。由此,我对山水画的写生创作观有了“游之、记之、悟之、写之”的创作感悟。
蒋海峰走向凉台,异常镇静,凝望着深邃的夜空,从来没有这样美。他似乎听到了上帝的召唤,爬上栏杆,轻轻一跃,结束了一切恩怨,结束了苦痛的一生。
在式(14)中,与x相比,时间t并无特殊之处,所以我们也可让从S到S′的时间缩放系数与从S′到S的相同,即
1 线性时空变换的证明
式(8)代入式(7),并整理可得

图 1
图1中P(或称事件)在S中的坐标为(x,t), 在S′中的坐标为(x′,t′)。两个坐标系所看到的是同一个事件,所以必然有如下的函数关系

(1a)
(1b)
当然式(1)也必须是可逆的,以保证一一对应。
1.1 时空均匀和各向同性的要求
对式(1)取微分有

(2a)
(2b)

(3)
容易求得偏微分方程(3)的解为
(4)



(5)
容易求得偏微分方程(5)的解为
(6)

注意式(2)的dx可以沿x轴的正向,也可以沿x轴负向,即式(3)和式(4)的成立要求空间沿x轴两个方向是同性的(对于空间问题,则进一步要求沿y和z同性;不仅如此, 沿x,y和z三轴任意组合的方向也是同性,即要求空间是各向同性的)。同样式(2)和式(5)要求时间沿正向和沿反向也是同性的。
综上,式(2)到式(6)成立的前提为时空是均匀且各向同性。均匀指的是参数不随时空点而变化,而各向同性指的是有方向的物理量,在不同方向上也是相等的。

1.2 惯性定律的要求
在外人眼里,老伴是个贤妻良母,在我看来,老伴仍然是个良母,可不是一个贤妻。年轻的时候,我们是同学,走到一起顺理成章,感情基础非常好。后来,有了孩子,生活的琐碎也没有影响我们的感情,小日子越过越滋润。没想到,到了晚年,因为忙碌小孙子的事,我们少了交流,遇到事情就会争吵,而且越吵越远。
x′=k1+k2t′
(7)
其中k1和k2是与x′,t′无关的常数(k1相当于初位置;k2相当于速度)。此时式(1)退变为

(8a)
(8b)
考虑两个平移的惯性坐标系S和S′,其中S′的坐标原点相对于S的速度为。因为垂直于的两个坐标的各自变换是平凡解,为简洁计,我们的焦点集中于沿相对速度的坐标x和时间t这两个量的变换关系,如图1所示。
或可进一步写为
(9)


x′=k3+k4t′
(10)
其中k3和k4是与x′,t′无关的常数。此时式(1)退变为
工程法律风险是产生于项目实施过程中,由于行为人的具体行为不规范而导致的,与企业或项目预期目标相违背的法律不利后果发生的可能性。法律风险发生于工程运作过程中,法律风险控制是工程项目管理的重要手段,是全面风险管理的重要支撑。加强工程法律风险管理具有重要的现实意义和经济效益,是油田企业工程项目的内在要求,是企业适应内外部环境变化的必然选择,是提升管理水平、实现跨越式发展的迫切需要。
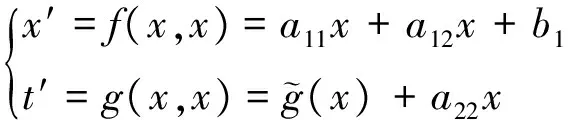
(11a)
(11b)
式(11)代入式(10)整理得到
(12)

将式(9)和式(12)分别代入式(4)和式(6), 就有如下的线性变换
(13)
这即证明了时空变换的线性性质。在这个性质证明中,时空均匀性、时空各向同性和惯性坐标系的等价性等三性缺一不可。
(3)CA-074预处理组(CA-074+LPS组):腹腔注射组织蛋白酶B抑制剂CA-074 10 mg/kg,30 min后腹腔注射致死剂量LPS。
不失一般性,我们可把式(13)进一步限制为标准型,即(x′,t′)=(0,0)与(x,t)=(0,0)对应,这就有b1=0,b2=0。随后只讨论如下的标准型,
(14)
如果放弃时空均匀性和各向同性,只要求惯性系的等价性,自然就不能从式(4)和(6)出发了。读者可参考文献[8]对此情形的处理。
2 洛伦兹变换的推导
2.1 对伽利略变换缩放系数的拓展
在牛顿时空下有伽利略变换x′=x-vt,t=t′,它的缩放系数满足
第三,加强教师专业指导,保障集体实践活动的有效开展。 集体实践活动虽然应该充分尊重学生的主体地位,更多地鼓励学生积极参与。 但是在实践过程中,学生难免会遇到各种无法解决的问题,这就需要来自教师的专业指导。 学校应选派工作经验丰富、理论功底深厚的教师参与实践活动。 专业指导教师一方面应积极参与实践活动的策划和审定环节,把握实践活动的方向性、科学性和可行性,保障集体实践活动的有效开展; 另一方面在活动的开展过程中,教师也应做到积极参与,引导大学生群体在实践过程中体悟和践行集体主义原则,保障实践活动教育功能的发挥。

(15a)
(15b)
由于从伽利略变换所导出的预测与接近光速的实验结果不吻合,所以要对其修改。一种修改就是放宽式(15)的要求。当然,随意放宽也不尽合理,比如a11=1000就相当于在S的长度单位为m,而S′为mm。因度量单位不一致所造成的差异与物理本质无关。
一个较为合理的拓展是把式(15a)放宽成从S到S′的缩放系数与从S′到S的缩放系数相等,即
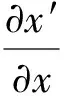
(16)
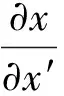
为了利用式(16), 从式(14)解出
(17)
其中行列式Δ=a11a22-a21a12。由式(17)有

(18)
式(16)变为

(19)
本文将首先从时空均匀性、时空的各向同性和惯性坐标系的等价性等三性出发,导出线性时空变换,然后再附加进一步的假设,推演洛伦兹变换。
在S′中看到S原点的速度v′为(利用式(25)的第一式和第三式)

(20)
由式(17)得到
