化归思想在初中数学课堂中的应用研究

井媛媛

化归思想是初中数学中常用到的一种数学思想，它能帮助学生有效解决数学难题，让问题不再复杂、陌生、抽象、困难，实现解题思路与方法的柳暗花明.因此，化归思想是备受师生青睐的一种数学思想方法，如何在课堂中渗透化归思想，让学生理解化归之精髓，继而可准确在数学解题中运用是数学教师的职责所在.在初中数学课堂中培养学生化归意识和能力，一方面是新课改的要求，另一方面是学生数学能力提升的要求.

一、巧用化归——削减问题的复杂系数

初中阶段是学生数学学习的关键时期，这一阶段学生数学学习的内容更加枯燥、复杂且困难.很多学生在解决一些复杂问题时往往抓耳挠腮，无从下手.巧用化归思想能削减问题的复杂系数，帮助学生轻松解决复杂难题，提升学习兴趣.

数学中有很多问题相当复杂，不仅文字叙述复杂，而且式子列出后的计算也更加复杂多变，学生如果不运用化归思想，要想解决此类难题，可谓难如登天.这里以一个复杂的一元二次方程为例来进行解析.题目2（x-1）2-5x+5+2=0乍看上去并无规律可循，很多学生就直接将前面的2（x-1）2展开来计算，但在计算的过程中，学生们会发现越来越复杂，越来越难解，于是花了很长时间计算出来，结果还容易算错.但我们仔细观察，就发现式子-5x+5可转化为-5（x-1）于是，原式子就成为2（x-1）2-5（x-1）+2=0.再观察，不难发现这是关于（x-1）的一元二次方程.于是，可利用化归思想让问题不再复杂.令y=x-1，解关于y的方程2y2-5y+2=0.这样，问题便显得更为简单，先前复杂的算法也尽可抛弃，这样计算出y的两个值分别是y1=2，y2= 1 2 .接下来，自然而然便计算出了x1=3，x2= 3 2 .原方程的解便是3与 3 2 ，问题迎刃而解.

化归思想能将复杂的问题轻松转化为更为简单、可解的问题.运用化归思想，学生能很快理清复杂问题的思路，并循着路径一步步地，将问题又快又准确地计算出来，学习自信心也极大提升.

二、引入化归——使陌生问题更加熟悉

学生们对自己十分熟悉的问题更容易轻松解决，但对于那些新颖、陌生，从未见过的题目往往持有恐惧与排斥心理.引入化归思想，能尽可能将陌生、新颖的难题熟悉化、日常化，让学生在熟悉的解题感觉中，找到解题路径与技巧，实现陌生难题的轻松解决.

教师要懂得在课堂中培养学生的化归意识，巧妙引入化归思想，让学生在潜移默化中学会使用化归思想.初中生刚接触不等式时，难免诚惶诚恐.例如，教师展示了一个陌生的不等式问题：y-5≤2，2，4，8，11，5，9，7这些数字哪一个是不等式y-5≤2的解.初次见到此类问题，学生总是一头雾水.教师在讲解的过程中，可利用化归思想，将这一问题转化为学生最熟悉的一元一次等式问题，即y-5=2，最后解得方程的解为y=7.这样教师再引导学生对不等式y-5≤2进行简单的分析，而要想满足不等式y的值自然要符合y≤7.这样，学生们马上就能顺利解决原问题，找出2、4、5、7几个数字符合原不等式，理应是原不等式y-5≤2的解，其他的则不是.一元一次不等式是初中生接触的一个新的知识点，教师巧用化归思想可让学生轻松理解不等式内涵，这为以后学生学习和解决更为复杂的不等式问题奠定了坚实基础.

巧用化归思想，可以让一些看起来十分陌生的数学问題更为熟悉，实现了新旧知识的巧妙链接，这对学生顺利解决问题十分有益.无论是解决哪种陌生问题，教师都要能引导学生巧用化归，解决问题.

三、渗透化归——让抽象问题变得具体

初中数学问题已经变得相当抽象，很多问题不仅题目抽象，所给的条件更为抽象，让人无从下手.这时候，学生更应巧用化归思想，让抽象的问题具体化，找寻题目中有价值、有意义的信息，猜测出解决问题的关键所在.这样，问题才会迎刃而解.

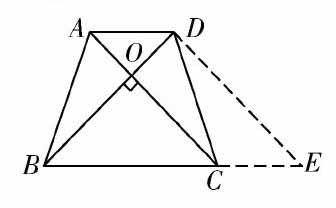
初中数学中，往往会有一些比较复杂的几何图形问题，从题目已知信息和所给图形来看，根本找不出任何问题解决的线索，这就需要学生巧用化归思想，借助辅助线将抽象问题具体化，找出解决思路.例如，已知等腰梯形ABCD（如图所示），

等腰梯形的两条对角线相交于O点，AC与BD垂直，AB=CD，且AC=3，BD=5，求AC的长度.该题目乍一看，无解（没做辅助线之前），因为整个图形光秃秃的，题目中有效信息都用上了，还是找不到解题思路.于是，学生可考虑使用化归思想，将原图中的AC和AD进行平移，分别做辅助线DE和CE，经过辅助后的图形显得不再抽象，而变得具体可解.原题目中很多信息都可用到.要想求AC的值便是求DE的值，这样便可将求DE的值放在等腰三角形DBE中去求解，问题便简单得多.

以上案例是化归思想将抽象问题转化为具体形象问题，降低题目难度系数的一个实例.可见，在一些抽象的几何问题中，学生切忌盯着原图苦思冥想，而是应该活跃思维，巧用化归，多做辅助线，让抽象问题具体化.

总而言之，化归思想是初中生必须掌握的一种数学思想，也是一种解题技巧.这种技巧可削减困难问题的复杂系数、能让陌生问题变得熟悉可亲，还能让那些无比抽象难解的问题变得更加形象具体.化归是数学解题的法宝，教师在日常教学中，要不断更新教学方式、方法，将化归渗透于数学课堂教学中.唯此，学生的化归意识才能逐步增强，运用化归思想的能力也会发生质的提升，一举两得.