径向极化压电陶瓷管建模与仿真

杨明明，汪焰恩，魏生民，柴卫红，魏庆华

（1. 西北工业大学 机电学院，陕西 西安 710072；2. 西北工业大学 现代设计与集成制造教育部重点实验室，陕西 西安 710072）

研究与试制

径向极化压电陶瓷管建模与仿真

杨明明1,2，汪焰恩1，魏生民1,2，柴卫红1，魏庆华1

（1. 西北工业大学 机电学院，陕西 西安 710072；2. 西北工业大学 现代设计与集成制造教育部重点实验室，陕西 西安 710072）

基于平面应变假设，推导了径向极化压电陶瓷管在外电场作用下形变的计算公式。作为挤压式喷嘴的执行器，径向极化压电陶瓷管在与极化方向一致的外电场的作用下主要发生径向变形。利用有限元分析软件ANSYS14.0，对模型进行有限元仿真。利用这两种方法计算不同结构尺寸的压电陶瓷管在100 V电压作用下的内壁径向位移，两种方法计算结果之差小于 5%，结果的一致性，验证了理论公式的正确性。该理论分析模型可预测挤压式压电喷嘴在外电场作用下的响应，指导喷嘴结构设计，降低喷嘴设计成本，提高喷嘴结构设计可靠性和设计效率。

压电陶瓷管；理论分析；径向位移；有限元分析；挤压式；压电喷嘴

作为一种新兴的快速成形工艺，微滴喷射已在微结构制造、生物制造、功能梯度材料制备等许多领域得到了广泛应用。自从美国学者 Vladimir和Boland于1999年提出“生物打印”（Organ Printing，又译作“器官打印”）的概念以来[1]，利用快速原型技术实现生物活性材料的三维打印已成为目前生物制造领域的研究热点[2-3]。国内外研究者已通过改造压电文件打印机的方法验证了生物打印的技术可行性[4-6]。然而，目前文件打印机，特别是打印喷头很难实现高黏度材料的打印，故重新研发可打印高黏度生物活性材料的压电喷嘴对于实现和研究生物打印技术具有重大意义。

压电喷墨利用喷嘴上压电陶瓷（执行器）的逆压电效应，在外电场的驱动下使得喷嘴液腔壁产生机械位移，改变液腔体积，从而在液腔内部产生压力波，利用压力波驱动墨水形成液滴，并从喷嘴喷出。按照压电陶瓷的位置及极化方式的不同，压电喷嘴包括撞击式（Push）、弯曲式（Bend）、剪切式（Shear）及挤压式（Squeeze）四种典型结构[7]。撞击式和剪切式结构以其结构紧凑，便于集成在多喷嘴喷头中的特点在当前文件打印领域得到了广泛应用，而挤压式结构与墨水有较大的接触面积，可望利用该结构实现高黏度材料的打印。相应地，新加坡学者Li等[8]于2010年研发了以PET/PTFE材料作为衬底材料的压电挤压式喷头，该喷头打印黏度可达0.1 Pa·s，大大高于一般商用打印喷头的黏度上限（大部分商用打印机打印黏度不高于 0.02 Pa·s）。

建立准确的理论模型是优化喷嘴结构、提高打印性能和打印材料范围的基础。特别是由于喷嘴尺寸通常非常小（特征尺寸1～100 μm），且液滴生成时间很短，这使得实验研究喷射原理非常困难且实验成本昂贵[7]。准确的理论分析模型可初步预测压电喷嘴在外电场作用下的响应，从而可以显著降低喷嘴设计成本，提高设计效率。本文针对挤压式压电喷嘴，基于平面应变假设，建立了挤压式压电喷嘴执行器的静力学模型，并利用ANSYS14.0商用分析软件对该执行器实施了力学仿真，验证了本文所建立模型的正确性。

1 挤压喷嘴结构及压电方程

所研究的挤压式压电喷嘴结构如图 1所示，内、外径分别为D1、D2，长度为L0的玻璃（或塑料）衬管内充满墨水，衬管的一端与输墨管相连接，另一端为直径为d的喷嘴；套在衬管外部的锆钛酸铅（PZT-5H）压电陶瓷管长为L，外径为D3；该陶瓷管的内外壁表面均覆盖有一层很薄的电极，电极层厚度远小于压电陶瓷管厚度，为简化结构，本文不考虑电极层对压电陶瓷管变形的影响。压电陶瓷管沿径向极化，由电极分布可知外电场方向同样沿径向方向。

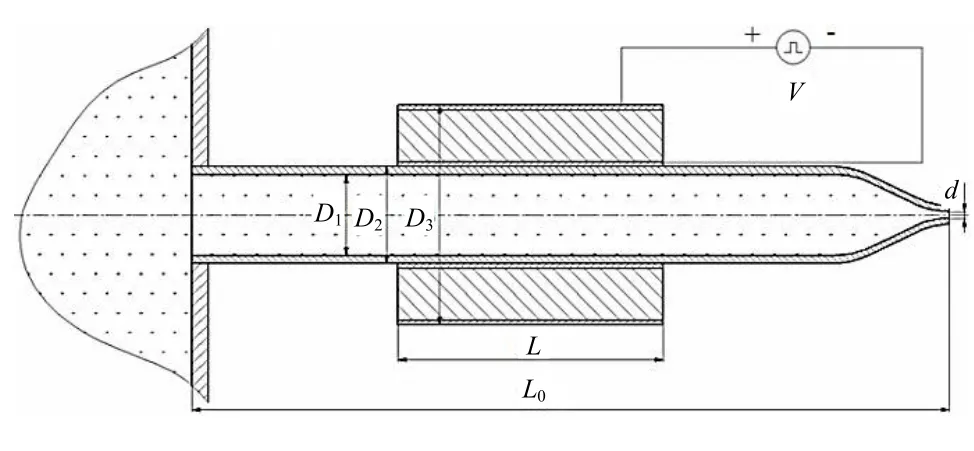
图1 压电喷头示意图Fig.1 Sketch diagram of piezoelectric nozzle

压电陶瓷在外加电场E的作用下，会产生与电场强度呈线性关系的机械形变，该现象被称为逆压电效应。逆压电效应可用压电方程[8]表示：

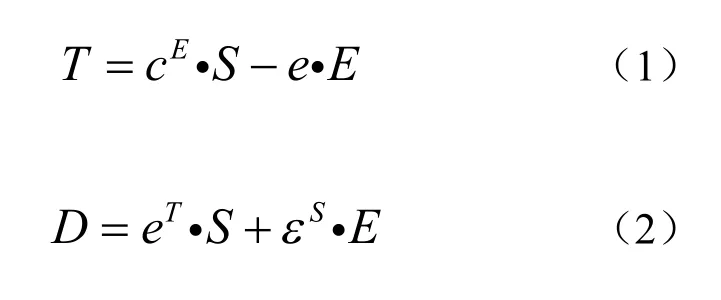
为了研究压电挤压管运动，还需综合考虑如下结构和静电方程[9-10]：

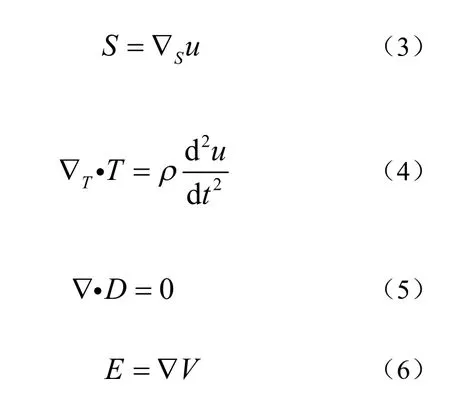
式中：T,S分别是应力矢量和应变矢量；cE，εs分别是压电陶瓷短路刚度矩阵及夹持介电常数矩阵；e为压电常数矩阵；u为位移矢量；D是电位移矢量；E，V分别是外电场强度矢量和电势；ρ为压电陶瓷密度；∇是哈密顿算子；分别为应变梯度算符和应力散度算符[10]。

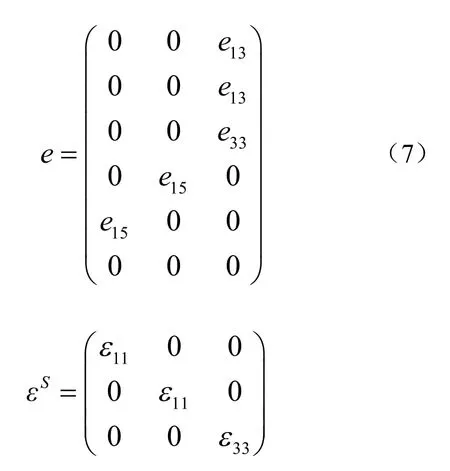
压电陶瓷材料属性与六方（6mm）点群相似，对于沿z轴极化的压电陶瓷材料其弹性矩阵cE、压电矩阵e和介电常数矩阵εs具有如下形式[9]：

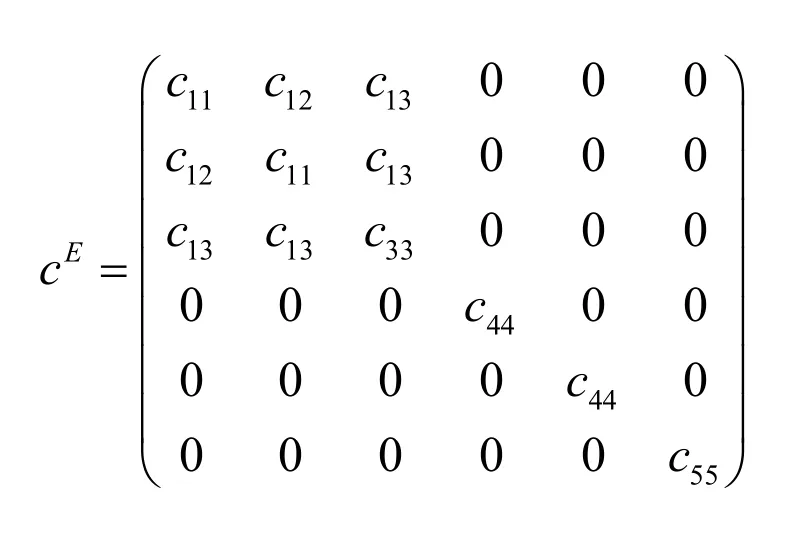
2 理论分析

选取柱坐标系为参考坐标系，z轴沿着微管中心线并指向喷嘴方向，根据结构和激励的特点可作如下假设：

（1）轴对称假设：此时，沿圆周方向的位移为零，且各场变量（如应力场、外电场等）与轴向坐标无关。

（2）平面应变假设：通常，为增大驱动面积，压电陶瓷管轴向长度L远大于径向尺寸，且外电场方向沿径向（与轴向垂直），故可假设压电陶瓷管属于平面应变问题范畴；此时径向位移与轴向坐标无关，且轴向位移等于零。

（3）电场E分布与轴向坐标z无关：压电陶瓷管内外表面为等势面，且轴向尺寸远大于径向大小，故可认为外电场在压电陶瓷管内分布与轴向坐标无关。

（4）内衬玻璃管壁厚（2～10 mm）远小于压电陶瓷厚度，分析时，可认为该内衬微管并不影响陶瓷管位移。

如上假设可写作：

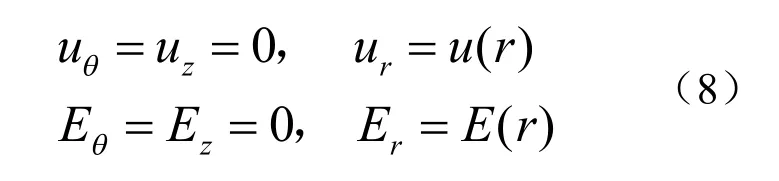
代入柱坐标几何方程（3）可得：

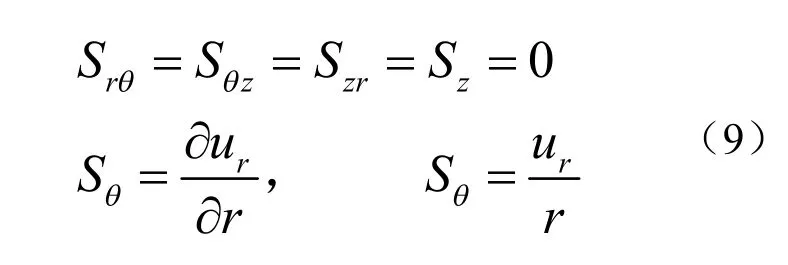
此时压电陶瓷管径向电场的作用下主要做径向伸缩运动，将式（8）和式（9）及材料矩阵（7）分别代入压电方程（1）、（2）可得：

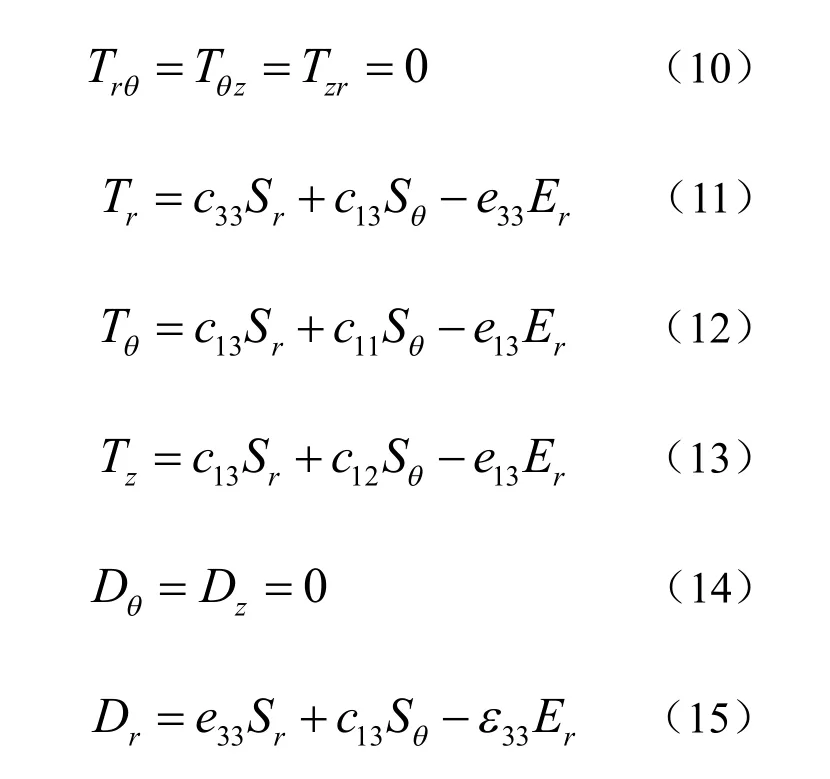
从而平衡方程（4）及静电方程（5）可化简为：

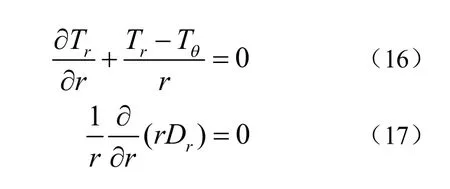
同时，径向场强应满足：

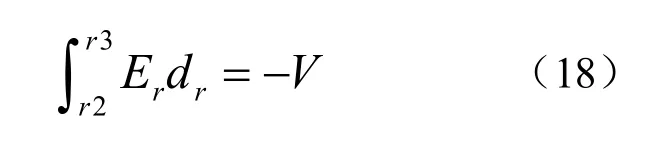
方程（8）～（18）即为压电陶瓷管在外电场作用下的静力学模型。

由式（15）知径向电位移Dr只是径向坐标r的函数，故式（17）可化简为：Dr=D0/r，其中D0为常数，将表达式代入式（15）可得：

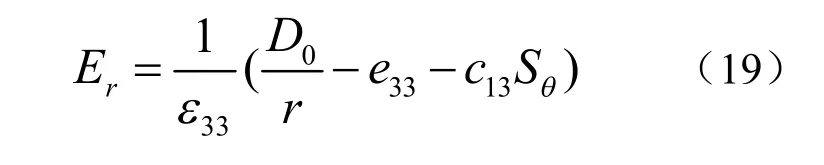
联立方程（9）、（11）、（12）、（16）和（19）可得径向位移ur的方程：

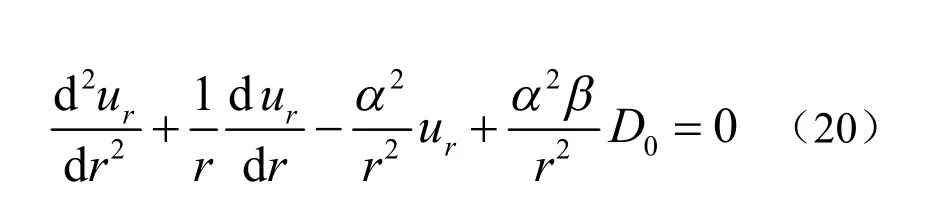
求解该方程可得：

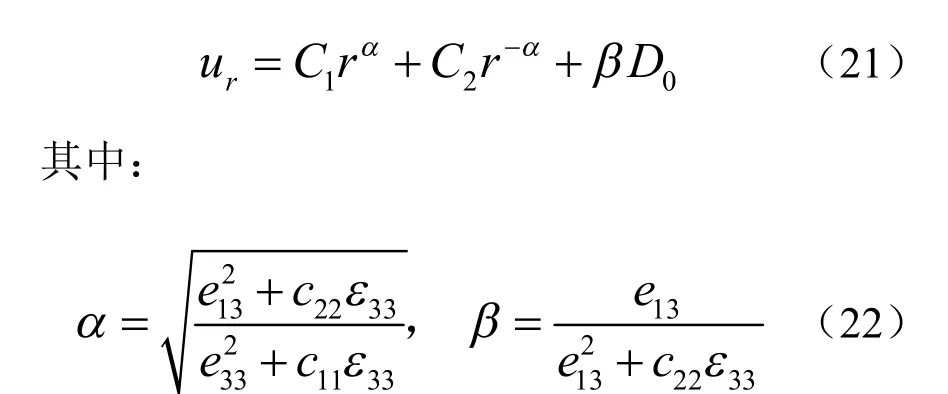
C1，C2和D0均为任意常数。由力学及静电边界条件:压电陶瓷管内壁处(r=r2=D2/2)径向应力Tr等于液腔压力P（由压力波在液腔中的传播规律决定），外壁自由；场强Er沿径向积分等于电势差V，即：

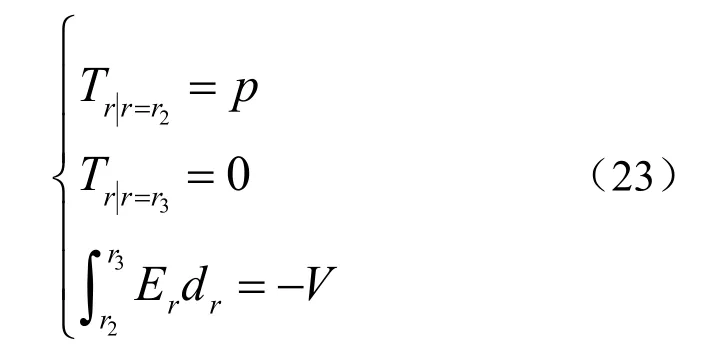
联立求解（23）所包含的三个边界方程组即可求得方程（21）中常数C1，C2和D0，具体表达式见附录。

3 计算与仿真实例

为直观说明压电陶瓷管在外电场作用下的响应并验证上文推导的理论模型，本文将分别使用所推导理论模型和 ANSYS商用有限元软件，计算参数如表1所述压电陶瓷管径向形变。

表1 结构尺寸Tab.1 Parameters of structure

PZT-5H压电陶瓷材料的材料属性[10]：

将上述参数代入方程（20），利用符号计算软件Maple求解参数C1，C2和D0。可计算得所述压电陶瓷管在100 V电压作用下ur表达式为：

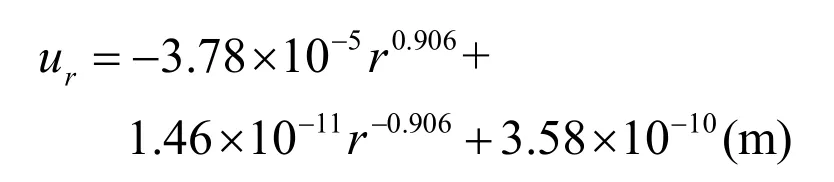
图2即为形变ur沿径向的分布曲线。

图2 径向位移沿壁厚分布曲线Fig.2 Curve of radial displacement changing with wall thickness

利用有限元分析软件ANSYS 14.0对该结构进行计算仿真，选用耦合单元Solid223来完成压电效应的仿真，有限元模型参数如表 2。利用后处理中的Path方法，可绘制ur关于径向坐标的分布曲线如图3所示。图4为分析所得径向形变ur的云图。

表2 ANSYS模型边界条件Tab.2 ANSYS model boundary conditions

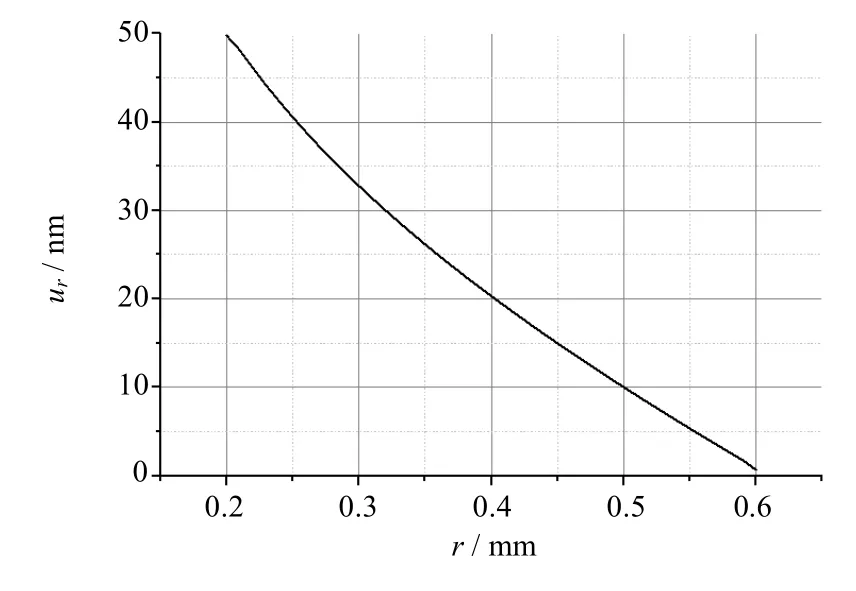
图3 ANSYS计算径向位移分布Fig.3 Radial displacement calculated by ANSYS

图4 径向位移云图Fig.4 Contour of radial displacement

比较图2与图3，可发现本文推导理论公式计算的径向形变分布与 ANSYS有限元分析结果吻合。压电陶瓷管内壁径向位移是决定挤压式压电喷嘴效率的决定性因素，表 3列出了理论公式与ANSYS有限元方法对内壁径向位移的计算结果，可以看出两者之差小于 5%，进一步验证了所推导模型的正确性。

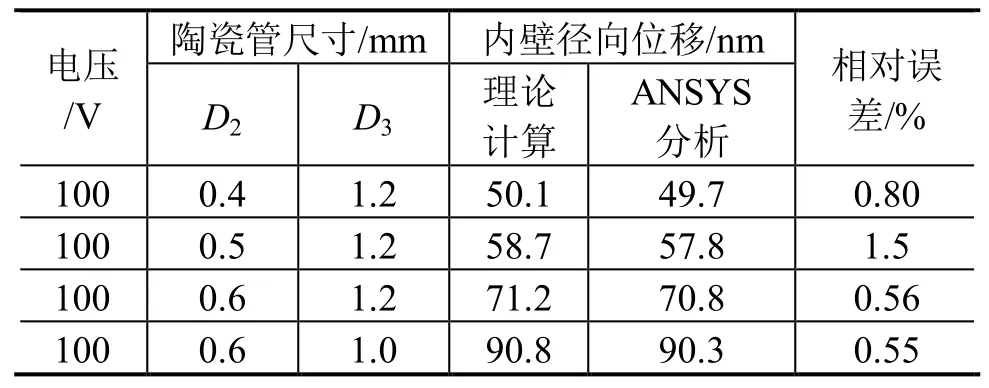
表3 内壁径向位移Tab.3 Radial displacement of inner wall

4 结论

本文基于平面应变假设，推导了作为挤压式喷嘴执行器的压电陶瓷管在径向电场作用下径向形变计算表达式。利用有限元计算软件ANSYS14.0，对模型进行有限元仿真，两种方法的计算结果之差小于 5%，结果的一致性，验证了理论建模的正确性。该理论模型的建立对于提高压电喷嘴性能和优化喷嘴结构具有重要意义。

[1] MIRONOV V, BOLAND T, TRUSK T, et al. Organ printing: computer-aided jet-based 3D tissue ring [J]. Trends Biotechnol, 2003, 21: 157-161.

[2] BOLAND T, XU T, DOMON B. et al. Application of inkjet printing to tissue engineering [J]. Biotechnol J, 2006(1): 910-917.

[3] RACHEL E S, JULIE E G, BRIAN D. Delivery of human fibroblast cells by piezoelectric drop-on-demand inkjet printing [J]. Biomaterials, 2008, 29: 193-203.

[4] 岳相辉, 曾甫清, 陈宏翔, 等. 细胞打印的可行性研究[J]. J Chin Urology, 2006, 10(21): 782-784.

[5] WILSON W C, BOLAND T. Cell and organ printing 1: protein and cell printers [J]. Anatomical Record Part A, 2003, 272A: 491-496.

[6] KIM J D, CHOI J S. Piezoelectric inkjet printing of polymers: stem cell patterning on polymer substrates [J]. Polymer, 2010, 51: 2147-2154.

[7] WIJSHOFF H. The dynamics of the piezo inkjet printhead operation [J]. Phys Rep, 2010(491): 77-177.

[8] LI E Q, XU Q. Design and fabrication of a PET/PTFE-based piezoelectric squeeze mode drop-on-demand inkjet printhead with interchangeable nozzle [J]. Sens Actuators A, 2010, 163: 315-322.

[9] 王春雷. 压电铁电物理 [M]. 北京: 科学出版社, 2009.

[10] 王矜奉. 压电振动理论与应用 [M]. 北京: 科学出版社, 2011.

Modeling and simulation of radial polarized piezo tube

YANG Mingming1,2, WANG Yanen1, WEI Shengmin1,2, CHAI Weihong1, WEI Qinghua1
(1. School of Mechatronics, Northwestern Polytechnical University, Xi’an 710072, China; 2. The Laboratory of Contemporary Design and Integrated Manufacturing Technology, Ministry of Education, Northwestern Polytechnical University, Xi’an 710072, China)

Based on plane strain hypothesis, radial displacement formula of polarized piezo ceramic cylinder excited by radial electric field was derived. Radial polarized piezo ceramic cylinder, which is actuator of squeeze-mode piezoelectric inkjet printhead, perform mainly radial deformation under radial external electric field. Finite element (FE) simulation was also carried out using the software of ANSYS 14.0. Inner surface radial displacements of different piezo tubes were analyzed using the two methods at 100 V. The difference between results of the analytic formula and FE simulation is less than 5%. Consistent results of two different methods verify qualification of the derived formula. The analytic model could be used to predict the response of squeeze-mode inkjet printer under external electric field, reduce design costs and improve design reliability and efficiency.

piezo tube; theoretic analysis; radial deformation; finite element simulation; squeeze-mode; piezoelectric printhead

10.14106/j.cnki.1001-2028.2018.01.005

TM28

A

1001-2028（2018）01-0023-05

国家自然科学基金资助项目（51175432）；教育部高校博士点专项科研基金资助项目（20116102110046）；中央高校基础研究基金资助项目（3102014JCS05007）；陕西省工业科技攻关项目（2015GY047）；西北工业大学博士论文创新基金资助（201213）

2017-10-08

汪焰恩

汪焰恩（1976－），男，江西婺源人，教授，主要从事人工骨设计与快速成型、计算机辅助数值分析；杨明明（1988－），男，甘肃天水人，博士研究生，主要从事生物压电打印工艺的研究。

附录：

ur方程中常数C1，C2和D0计算公式：

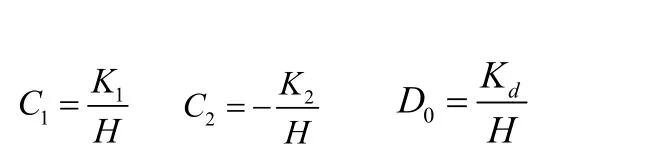
其中：

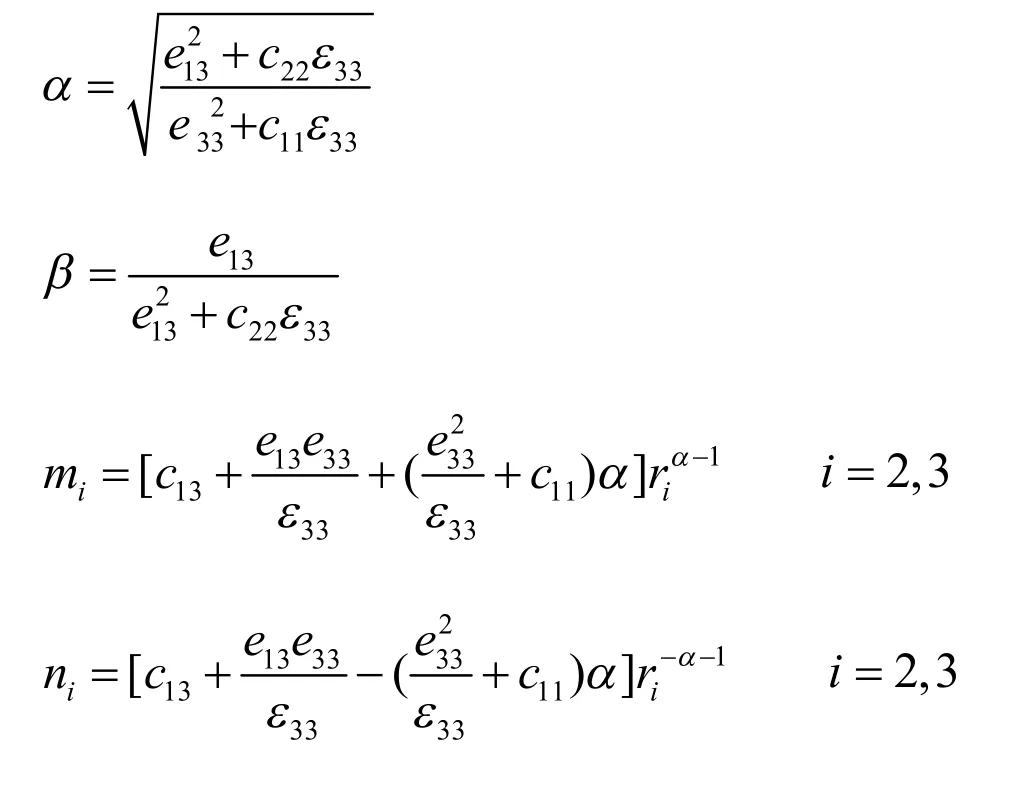
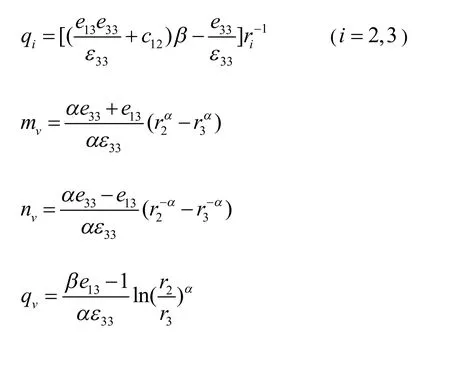
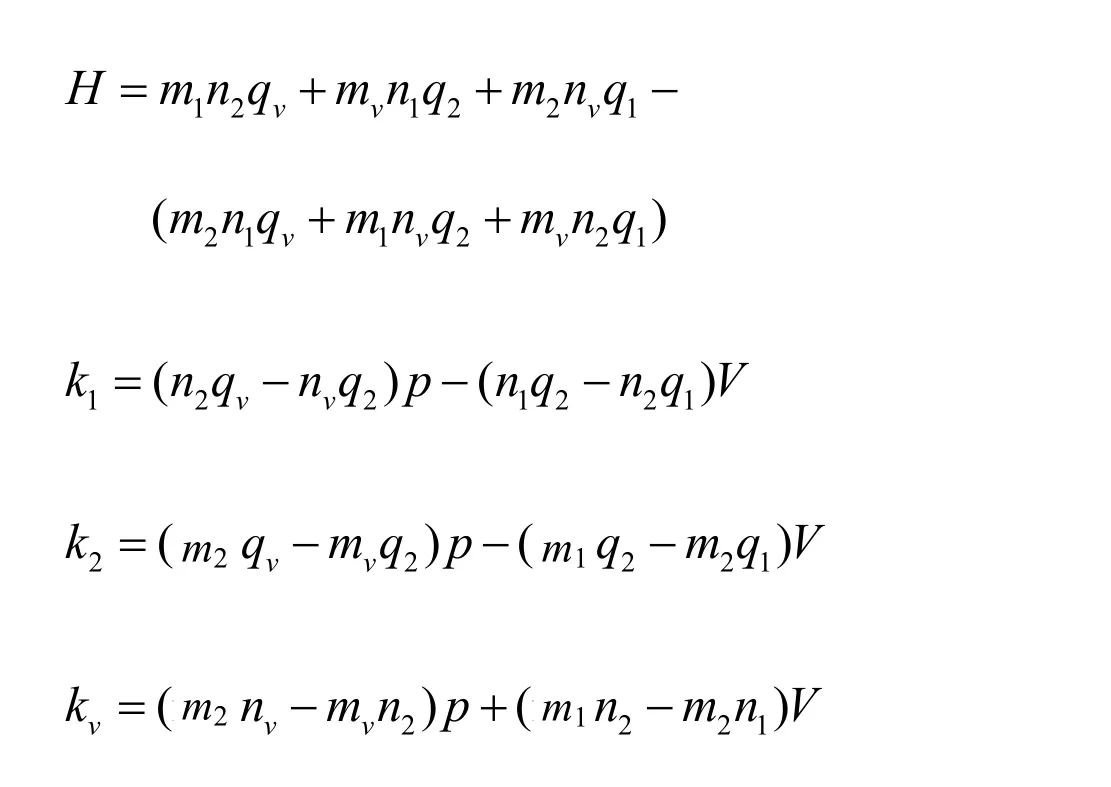
曾革）