40 m跨度波形腹板组合连续梁桥波型优选分析
2018-01-05尤涛宁郑凯锋
尤涛宁, 郑凯锋, 谢 悦, 滕 乐
(西南交通大学, 四川成都 610031)
40 m跨度波形腹板组合连续梁桥波型优选分析
尤涛宁, 郑凯锋, 谢 悦, 滕 乐
(西南交通大学, 四川成都 610031)
波形钢腹板梁桥设计时通常根据经验选择波形,而未进行理论分析。针对这一问题,文章选择几种常见波形,建立有限元模型计算对比,找出适合的波型,为波形钢腹板桥选择合适波形提供参考。同时将有限元结果与已有理论进行比较,验证有限元建模的准确性,检验结论可靠性。
波形钢腹板; 组合桥; 波形; 有限元
减轻大跨度预应力混凝土桥梁上部结构重量是桥梁技术革新的重要方向,各国工程师为此进行了各种探索。1975年,法国Campenon Bernard公司最先提出使用波形钢腹板的假设,并于1986年在法国建成世界上首座波形钢腹板预应力组合梁桥Cognac桥。20世纪末,日本引进法国波形钢腹板组合桥的技术并进行深入研究。在近20年的时间里,日本建设了约200座波形钢腹板桥,拓宽了波形钢腹板组合桥的使用范围并完善了其设计和施工技术。此外,德国、挪威、委内瑞拉等国家也先后在桥梁建设中应用这一结构。我国对波形钢腹板组合桥的研究开始于20世纪90年代,起步较晚,经验较少,规范仍不完善。
本文以河南某4×40 m波形腹板组合连续梁桥设计方案为例,利用我国规范中推荐的三种波型,应用MIDAS FEA有限元数值模拟方法计算波形钢腹板受力情况,为波形钢腹板桥选择合适波型提供参考。
1 设计方案和试算波形腹板
40 m跨度波形腹板梁组合连续梁桥(以下简称桥梁)桥面板采用C50混凝土,波形钢腹板及上下翼缘板采用Q345D,全桥纵向和横向均无预应力,普通钢筋为HRB400。桥梁分两幅,双向10车道,单幅桥面包括3个机动车道、非机动车道和人行道,人行道宽5 m,非机动车道宽5 m,行车道总宽24 m,设计采用公路-I级荷载,车道布置如图1所示。
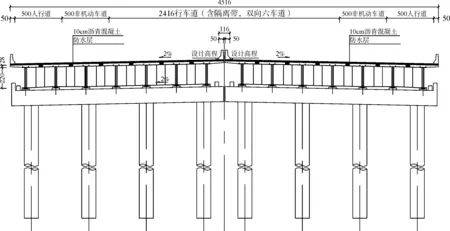
图1 标准横断面(单位:m)
桥梁由7片主梁组成,梁高2.45 m,双幅全宽45 m,单幅桥宽22.5 m,翼缘板悬长1.55 m,顶板为普通钢筋混凝土结构,厚0.25 m。在每跨支点、跨中、1/4跨、3/4跨处设12 mm厚实腹式横隔板,上下翼缘宽度均为0.8 m。根据承载能力需要上翼缘厚度有16 mm、22 mm,下翼缘厚度根据受力需要有20 mm、30 mm和40 mm三种厚度,波形钢腹板厚度分为16 mm和22 mm两种。上下翼缘与腹板厚度具体分布如图2所示。

图2 波形钢腹板板梁桥立面布置(单位:mm)
我国规范[1]中推荐的波型有三种,波长分别为1 600 mm、1 200 mm和1 000 mm,各波形具体尺寸如图3所示。其中,1600型多用于大跨径桥梁,1200型与1000型多用于因运输条件所限需较短的波长与波幅的桥梁。本文欲通过比较三种波形钢腹板在受力、变形情况,选择最合理、经济的波形。
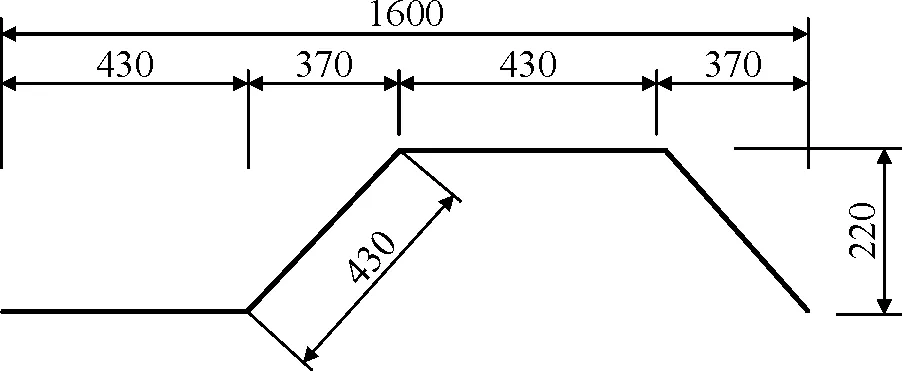
(a) 1600型
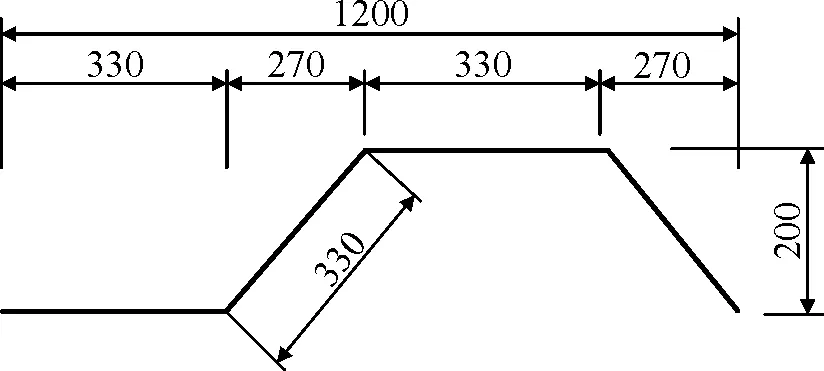
(b) 1200型
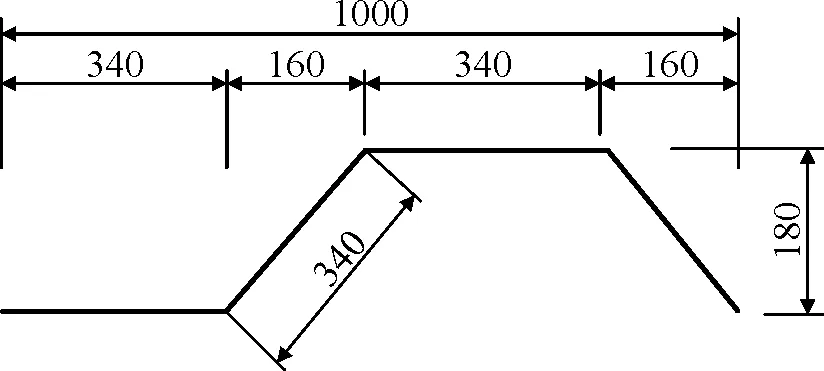
(c) 1000型图3 波形尺寸(单位:mm)
2 有限元模型建立
2.1 模型建立
应用MIDAS FEA建立有限元模型,桥面板采用实体单元模拟,钢板梁、横隔板结构采用板单元建模,实体单元模拟板式橡胶支座,橡胶弹性模量E=500 MPa。忽略桥面板普通钢筋对刚度的影响,不考虑波形钢腹板与桥面板间的相对滑移,分别建立不同波形的有限元模型(图4)。

图4 有限元模型建立
2.2 荷载取值
桥面板容重按25 kN/m3计,钢材容重按78.5 kN/m3计。人群荷载根据文献[1]按3.0 kN/m2计算。比较车辆荷载重轴布置在边支座的情况和布置在边跨跨中两种情况。车辆荷载布置在边跨跨中的情况剪应力与挠度均较大,在此列出车辆荷载布置在边跨跨中的挠度和剪应力分布。
3 荷载作用计算
分别提取三个模型在荷载作用下的挠度及主梁应力。由于波形钢腹板承担的弯矩与顶、底板相比极小,可以忽略[2],因此在进行应力分析时提取各单元剪应力。
3.1 自重作用应力计算
因自重作用下三个模型的挠度较小且波形钢腹板用量存在差异,同时存在波形不同及波形钢腹板用钢量不同两个变量。各波形的用量统计见表1。

表1 波形钢板用量 t
因此,除建立三个基本模型外,另建立三个不考虑波形钢腹板的容重的模型,仅考虑波形钢腹板刚度,以此排除腹板用量对挠度的影响。图5~图7中分别列出不同波形的主梁在自重作用下的剪应力分布。

图5 1000型自重作用下的剪应力(单位:MPa)

图6 1200型自重作用下的剪应力(单位:MPa)

图7 1600型自重作用下的剪应力(单位:MPa)
由图5~图7数据可知,1000型波形钢腹板在自重作用下的最大剪应力为15.1 MPa,1200型波形钢腹板的最大剪应力为14.9 MPa,1600型波形钢腹板的最大剪应力为14.6 MPa。可见,1600型波形钢腹板板梁桥在自重作用下应力较小。
3.2 自重作用变形计算
不同波形的波形钢腹板梁板梁桥在自重作用下的挠度计算结果见表2。

表2 自重作用挠度 mm
由表2可知,1600型波形钢腹板的挠度最小,为13.1 mm,1000型的挠度最大,为14.1 mm。
在桥面板相同的情况下,忽略PBL剪力键用量的影响,且排除波形钢腹板用量的影响后,荷载作用下挠度的差异主要原因是波形性能的不同。根据表3可知,排除波形钢腹板重量对挠度的影响后,各波形钢板梁挠度的大小排序与计入波形钢腹板自重的结果相同。1600型波形钢腹板挠度最小,1000型最大。

表3 修正后自重作用挠度 mm
3.3 移动荷载应力计算
图8~图10分别列出三种型号波形钢腹板主梁在移动荷载作用下的剪应力分布。

图9 1200型移动荷载作用下的剪应力(单位: MPa)

图10 1600型移动荷载作用下的剪应力(单位: MPa)
从图8~图10可见,移动荷载作用下各种波形钢腹板的剪应力分布基本相同,在中间支座处应力较大,远离支座处剪应力较小。1000型波形钢腹板板梁桥在车辆荷载作用下的最大剪应力为18.4 MPa,1200型的最大剪应力为18.3 MPa,1600型波形钢腹板板梁桥的应力较小,最大剪应力为17.8 MPa。
3.4 移动荷载变形计算
三种波形的波形钢腹板梁板梁桥在移动荷载作用下的挠度计算结果见表4。

表4 移动荷载作用挠度统计 mm
移动荷载作用下,1600型挠度较小,为16.7 mm,1000型波形钢腹板挠度最大,为18.2 mm,1200型挠度居中。
4 结果分析
4.1 应力分析
文献[4]通过比较同等外荷载作用下不同弯折角度的腹板剪应力大小,得出结论:30.7°弯折角腹板的计算结果最接近于理论结果,大弯折角度可提高腹板承担竖向剪力的比例,使混凝土承担的剪力更小。1600型的弯折角度为30.7°,1200型为36.5°,1000型的弯折角度最大为45°。
4.2 变形分析
波形对挠度的影响较大,1600型波形钢腹板在荷载作用下与1000型及1200型相比挠度较小。文献[6] 结合波形钢腹板箱梁的特点,应用初等梁理论,提出该种梁的挠度计算公式。他们认为,波形钢腹板梁的变形由弯矩引起的翼缘弯曲变形和由剪力引起的腹板剪切变形两部分组成。由剪切变形引起的挠度与弯矩引起的挠度百分比为:

(1)
式中:EhIh为混凝土板的抗弯刚度;Ge为波形钢腹板有效剪切模量,用公式4-3[5]计算。
文献[6]建议采用文献[5]按式(2)计算,各符号含义见图11。
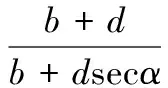
(2)
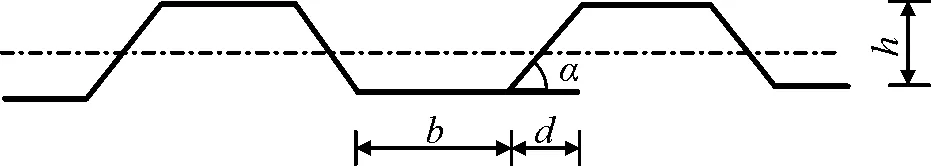
图11 波形钢腹板截面尺寸
通过计算,不同波形的有效剪切模量大小关系如下:
Ge1000∶Ge1200∶Ge1600∶G=0.883∶0.896∶0.930∶1
各模型在荷载作用下的挠度Δ=ΔM+Δv,根据式(2)可知,挠度公式也可写作Δ=ΔM×(1+U)。由结构力学可知,ΔM与刚度、计算跨径、 荷载有关。三个波形钢腹板板梁桥的挠度采用不考虑腹板中梁的修正挠度,在同一位置的截面弯曲刚度相同,因此ΔM相等,挠度Δ的差异取决于剪切变形引起的挠度与弯矩引起的挠度百分比U,且与U成反比。即,在相同荷载作用下,1600型波形钢腹板挠度最小,1200型次之,1000型挠度最大,这与有限元计算结果相吻合。
5 结束语
(1)通过理论分析,1600型波形钢腹板是三种比较方案中最理想的波形,且有限元模型与理论计算结果相吻合。
(2)经计算,三种波形的波形钢腹板用量差距较小,经济性相同。因此,通过对受力、变形、用量分析,1600型波形钢腹板是三种波形中最适合本桥的。
[1] 中华人民共和国交通运输部.JT/T 784-2010 组合结构桥梁用波形钢腹板[S].北京:人民交通出版社, 2015.
[2] 中华人民共和国交通运输部.JTG D60-2015 公路桥涵设计通用规范[S].北京:人民交通出版社, 2015.
[3] 聂建国. 钢-混凝土组合结构桥梁[M].北京:人民交通出版社,2011: 305-309.
[4] 赵磊,王涛,张兴,等. 波形钢腹板梁桥腹板抗剪强度特性分析[J]. 公路与汽运,2016(6):165-169.
[5] John R P, Cafolla,J . Corrugated webs in plate girders for bridges. [ J ] . Structures and Buildings , 1997 ,123(5):157-164.
[6] 李宏江,叶见曙,万水,等. 剪切变形对波形钢腹板箱梁挠度的影响[J]. 交通运输工程学报,2002(4):17-20.
[7] 徐岳,朱万勇,杨岳. 波形钢腹板PC组合箱梁桥抗弯承载力计算[J]. 长安大学学报: 自然科学版,2005(2):60-64.
[定稿日期]2017-08-02
尤涛宁(1992~),女,在读硕士,研究方向为钢桥与组合结构桥梁。
U443.35
A
