利用一元线性回归方程计算盗伐林木材积试验
2018-01-05粟军
粟 军
(西双版纳布龙州级自然保护区管护所,云南 景洪 666100)
利用一元线性回归方程计算盗伐林木材积试验
粟 军
(西双版纳布龙州级自然保护区管护所,云南 景洪 666100)
盗伐林木案件中,如现地伐桩保存完好,但无采伐木,周围有林相、结构相同或相近林分的情况下,利用样木的根径和胸径测量数据,建立线性回归方程计算出盗伐林木的回归胸径,再利用其树高的测量数据建立树高曲线对数回归方程,计算出盗伐林木的回归树高,并利用统计学原理,对回归胸径进行相关系数检验,对回归树高进行F检验。试验结果认为,利用该方法能使盗伐林木的蓄积量计算值更加接近实际值。
盗伐林木;胸径回归;树高回归;一元线性回归;二元材积;相关系数检验;F检验;材积计算
在《云南省林地鉴定规范(暂行)》第十七条规定中,关于现地伐桩保存完好,但无采伐木,周围有林相、结构相同相近林分的,直接每木检尺伐桩、鉴定树种、查数年轮,统计株数。在有代表性的地段设标准地,建立胸径与根径回归公式、胸径与树高的回归公式或树高曲线图,用二元立木公式计算蓄积。根据上述规定,在盗伐林木案件中可以借鉴上述规定和方法计算林木蓄积。
1 实验目的
通过实验,验证一元线性回归分析方法计算现地伐桩材积的可行性,了解一元线性回归分析方法和原理在计算现地伐桩材积中地应用,使理论与实践相结合,并把此方法更加紧密地应用于计算现地伐桩材积中。
2 实验方法
外业工具有测树围尺、测高器、皮尺、GPS仪、地形图等。用测树围尺测量16棵被盗伐银叶锥根径(D5cm),在盗伐林木现场周围对42棵坡向、林相、结构、树种相同的样木的根径(D5cm)、胸径(D130cm)用测树围尺测量,用测高器测量样木的树高。盗伐林木根径测量数据详见表1,样木测量数据详见表2。内业整理需电脑一台,把外业测量的盗伐林木伐桩数据、样木的根径、胸径、树高数据录入Excel文件中。
2.1 胸径回归
2.1.1 建立回归模型
利用样木的根径和胸径的测量数据,建立线性回归。预测对象“胸径”作为因变量y, 将主要影响因素“地径”作为自变量x,它们之间的关系用一元线性回归模型表示为:y=a +bx。
参数计算公式为:

快速计算方法:应用Excel插入散点图,添加线性趋势线,Excel可自动计算出a、b参数,用线性回归方程推算被采伐木的胸径(图1)。 经计算,a=-0.382 1,b=0.926 9。
2.1.2 相关系数检验
相关系数是描述两个变量之间的线性相关关系的密切程度的数量指标,用R表示。当R=1时,变量x、y完全正相关;R在-1~1之间,当0﹤R﹤1时,变量x和y正相关,当-1﹤R﹤0时,为负相关;当R=0时,变量x和y没有线性关系。通过应用Excel插入散点图,添加线性趋势线计算出R值后,查相关系数检验表,在自由度N-2(N为样本个数)和显著性水平a(一般取a=0.05)下,若R大于临界值,则变量x和y之间线性关系成立,否则两个变量不存在线性关系。
在自由度(f=n-2, 即f=42-2 )和显著性水平a=0.05的情况下,查“相关系数临界值表”得值0.304 4。通过计算,相关系数R=0.963 ,大于临界值0.304 4,且R值接近1 ,说明不但该地林木根径x与胸径y之间的线性关系成立,而且线性关系显著,说明以该地被采伐林木根径推算被采伐林木胸径准确度高。利用回归方程y=0.926 9x-0.382 1计算采伐木回归胸径结果详见表2。

表1 样木根径、胸径、树高

表2 胸径回归统计
2.2 树高回归分析计算
1)利用调查样木的胸径和树高的测量数据作为树高曲线的基础数据(表1)。
2)剔除样木异常数据。把测量数据按升序排列,然后利用这些数据绘成胸径树高曲线散点图(图2),利用这个散点图用肉眼剔除不可靠数据(表3)。
3)根据样木胸径树高的关系生成胸径树高曲线散点图,利用胸径树高对数曲线回归公式y=aln(x)+b计算回归分析后的树高,式中y为回归树高、a、b为参数、ln为自然对数、x为回归胸径。
a、b参数计算公式:把样木胸径转换为自然对数值,即x=ln(x), 然后利用上述一元线性回归模型y=a+bx及参数公式计算出对数回归曲线公式中的a、b参数。快速计算方法:在Excel中插入散点图,添加对数趋势线自动计算出a、b参数a=7.501 5、b=-11.85 。
4)在Excel中计算出整化后的回归胸径自然对数值ln(x),把对应的自然对数代入y=7.501 5ln(x)-11.85中,计算出回归后的树高(表4)。
5)对回归树高进行F检验
F检验计算公式为:
式中:F为统计量,s2为方差。
在样木中随机抽取16棵样木树高与回归树高进行F检验,在Excel 中进行快速F检验(表5)。
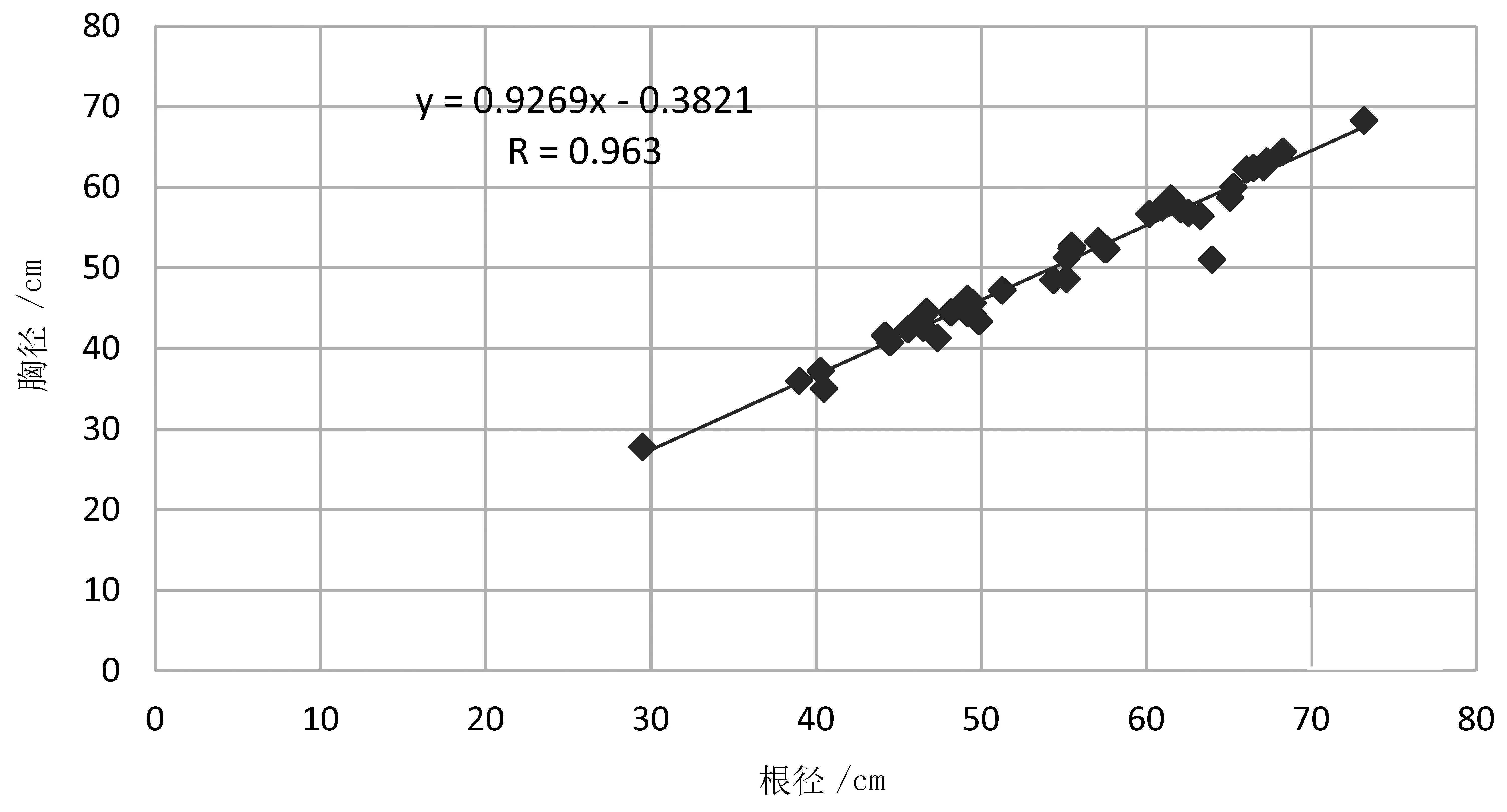
图1 根径胸径一元线性回归散点图Fig.1 Scatter diagram of unary linear regression between ground diameter and DBH
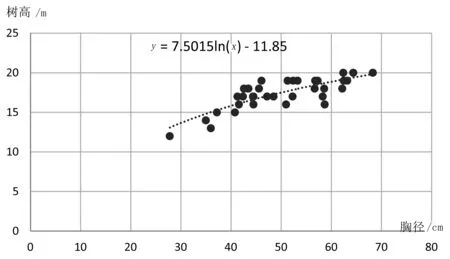
图2 胸径树高对数曲线Fig.2 Logarithmic curve between DBH and tree height
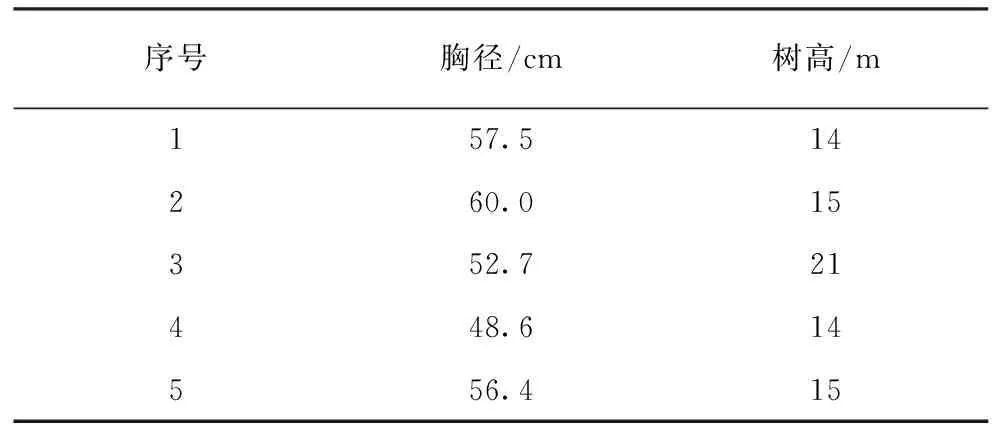
序号胸径/cm树高/m157.514260.015352.721448.614556.415

表4 树高回归计算统计

表5 F-检验 双样本方差分析
在表6中可以看到,F统计量为1.932 095 82,F单尾临界为2.403 447 07,F统计量
2.3 最小采伐量分析
假设在盗伐林木现场只盗伐了1棵林木,是否也可以用上述方法计算立木材积呢?假设在盗伐现场有一棵银叶锥伐倒木,根径(D5cm)为56.5 cm,胸径(D130cm)53.7 cm,树高为17 m。对伐桩利用硬阔一元材积公式计算得材积0.822 m3,胸径树高利用南亚热带阔叶树二元立木材积公式计算得材积1.661 m3。假设只有伐桩在现场,树干已运出林区,根据小样本容量n≥k+1(k为解释变量的数目)。利用在盗伐林木现场范围选取6棵坡向、林相、结构、树种相同和根径相似的样木进行以该地被采伐林木根径推算被采伐林木胸径准确度高。利用树高曲线对数回归公式计算得树高为18 m,利用回归后的胸径树高用南亚热带阔叶树二元立木材积公式计算得材积为1.711 m3。假设材积1.661 m3为实际值,利用一元材积计算得材积为0.822 m3,误差值为51.5%,利用回归胸径树高计算材积得1.711 m3,误差值为3.01%,说明利用回归后的胸径树高更接近实际值(表6)。

表6 小样本求材积统计
3 结论与讨论
3.1 结论
在云南省西双版纳州景洪市勐龙镇陆拉村委会松林新寨村小组集体林地内(现场中心坐标为E 100° 32′ 1.6″, N 21° 35′ 28.8″),对盗伐的16棵银叶锥伐桩和留在现场的伐倒木树干利用测树围尺和皮尺对根径、胸径、树高进行测量,并对周围林相、结构相同林分的42棵银叶锥样木利用测树围尺和测高器对样木根径、胸径、树高进行测量。对16棵盗伐的银叶锥分别利用硬阔叶树种根径一元材积公式、南亚热带阔叶树二元立木材积公式,以及利用回归后的胸径、树高用南亚热带阔叶树二元立木材积公式计算的蓄积进行对比(表7)。
经计算,对16棵盗伐林木根径数据利用硬阔叶树种根径一元材积公式计算得13.623 m3, 对胸径树高数据利用南亚热带阔叶树二元立木材积公式计算得28.024 m3, 对回归后的胸径、树高用南亚热带阔叶树二元立木材积公式计算材积得27.395 m3。假设16棵盗伐林木以28.024 m3材积为实际值,那么,利用硬阔叶树种根径一元材积公式计算得的13.623 m3与实际值误差为53.4%,利用回归后的胸径、树高用南亚热带阔叶树二元立木材积公式计算得的27.395 m3与实际值的误差为2.3%。表7对比说明,对盗伐林木伐桩保存完好,但无采伐木,周围有林相、结构相同或相近林分的情况下,对回归后的胸径、树高用二元立木材积公式计算得到的材积比根径一元材积公式计算的材积更接近于实际值。
3.2 讨论
盗伐林木案件中,现地伐桩保存完好,但无采伐木,周围有林相、结构相同相近林分的情况下,利用样木的根径和胸径的测量数据,在Excel中建立根径胸径线性回归散点图及线性回归公式计算出盗伐林木的回归胸径,利用样木的胸径和树高的测量数据,在Excel中建立树高曲线散点图及对数回归公式,计算出盗伐林木的回归树高,并利用统计学原理,对回归胸径进行相关系数检验,对回归树高进行F检验。通过试验,实现盗伐林木与样木拟合后利用二元立木公式计算蓄积,使盗伐林木的蓄积量通过线性回归更加接近实际值。
统计学一般经验认为,当样本量n≥30或者至少n≥3(k+1)(k为解释变量的数目)时,才能满足模型估计的基本要求。通过实验分析,对于盗伐林木在现场选择与盗伐木树种相同、根径相近和林相、结构相同或相近林分的立木做为样木,样木数量为n≥3(k+1)进行回归分析,是可行的。另外,对于同一样本数据和同一显著性水平,相关系数R检验、F检验、t检验3种检验效果具有等价性。在有关一元线性回归模型统计检验中,完全不必拘泥于选择哪一种统计检验,任选3种统计检验中的一种均可以做出同样的统计判断。

表7 蓄积量对比
[1] 李洁明,祁新峨.统计学原理[M].上海:复旦大学出版社,2010:1-453.
[2] 庞云海.已采伐林木蓄积量测算的应用实例及分析[J].林业调查规划,2006(5):13-17.
[3] 郭强,杨杰夫,施海波. Excel中自动完成方差齐性与非齐性t检验[J].湖南农业大学学报(社会科学版.素质教育研究),2007(1):18-23.
[4] 钱晓莉.回归方程的检验标准[J].财贸研究,1994(2):66-69.
[5] 王天营. 一元线性回归分析中三种检验的等价性研究[J].统计与决策,2011(3):8-11.
[6] 曹俊忠.一元线性回归显著性检验方法分析[J].西北纺织工学院学报,1988(3-4):78-82.
[7] 徐悦,陈昌华,蒋之富,等.天然赤松胸径与树高相关模型的研究[J].林业调查规划,2008(3):56-58.
[8] 王晓林,郭斌.柞树树高与胸径相关关系的研究[J].森林工程,2012(6):18-21.
[9] 伐桩现场勘验和林木蓄积计算方法[EB/OL]. 红安林业网.
Timber Volume Calculation of Illegal Logging with Unary Linear Regression Equation
SU Jun
(Bulong State-Level Nature Reserve Administration of Xishuangbanna, Jinghong, Yunnan 666100, China)
For the illegal logging cases, in which stump was preserved without cutting wood and surrounded by stand with the same or similar forest form and structure, the linear regression equation was set up to calculate the regression DBH of the illegal logging based on the data of sample trees’ ground diameter and DBH, and the logarithmic curve regression equation was set up to calculate the regression height of the illegal logging based on the data of sample trees’ height. With the principle of Statistics, the related-coefficient test of regression DBH and F-test of regression tree height showed that stock volume of the illegal logging calculated by this method was precision.
illegal logging; DBH regression; tree height regression; unary linear regression; dual volume; related-coefficient test; F-test; timber volume calculation
2017-07-10;
2017-07-17.
粟 军(1971-),男,云南勐腊人,工程师.从事3S技术应用、林地林木司法鉴定工作.
10.3969/j.issn.1671-3168.2017.05.003
S711;S758
A
1671-3168(2017)05-0014-06
