求解TSP问题的Flexsim仿真方法研究

（湖北汽车工业学院 经济管理学院，湖北 十堰 442002）

求解TSP问题的Flexsim仿真方法研究

张伟丰

（湖北汽车工业学院 经济管理学院，湖北 十堰 442002）

TSP问题是一类典型的组合优化问题，一般智能优化算法存在求解难度大、陷入局部解的问题。针对这些问题，提出了用Flexsim仿真软件求解此问题的方法，以旅行路线总距离最短为优化目标，建立了Flexsim仿真模型，并进行仿真运算，确定了最优旅行方案。通过对仿真结果进行分析，证明了此方法的有效性，较好地解决了旅行路径规划问题。

TSP；路径优化；仿真；Flexsim

旅行商问题（Traveling Salesman Problem，TSP）是典型的NP难题：一个旅行者由起点出发，访问n个城市，每个城市必须访问且只能访问一次，求解的目标是找出一条长度最短的路径。TSP问题应用广泛，很多现实问题都可抽象为该问题的求解，如车辆调度、机器人控制、路由器布设等，因此探索其优化方法具有重要的现实意义。目前很多群集智能优化算法被应用于TSP问题的求解，如模拟退火算法、遗传算法、粒子群算法、蚁群算法等［1］，在一定程度上能找到最优或接近最优路径，但仍然存在陷入局部最优解和收敛速度慢的问题。在实际应用中，这些方法的求解过程比较复杂，参数设置不当时求解结果的可信度往往不高，限制了其在实际中的应用。文中应用Flexsim仿真软件对TSP问题进行建模与仿真，并通过计算对比分析找出最优的路径组合。使用Flexsim仿真软件能快速建模并仿真，得出各类统计数据，在解决此类问题上更加方便快捷，相比其他方法更具实用性。

1 TSP问题数学模型

TSP问题数学描述如下：令G=(V,E)为赋权图，V={1,2,…,n}为顶点集，E为边集，各顶点间距离为dij，且(dij＞0，i,j∈V)，设

则数学模型表述为

式中：K是V的全部非空子集；|K|为顶点个数；式（2）为目标函数；式（3）～（4）表示经过每个顶点且只经过一次；式（5）保证没有子回路解的产生。

2 建立求解TSP问题仿真模型

2.1 构建Flexsim仿真模型思路

Flexsim软件是基于OpenGL技术开发的，有良好的三维效果，实现了建模仿真的可视化，数据信息可以方便地用软件中的模型库表示出来。求解TSP问题时，节点(城市)数量及距离等参数确定后，通过选择合适的实体，设置合理的参数，可构建符合需要的仿真模型，行走路线由随机数控制，在不同参数条件下对仿真模型反复运行，并对仿真结果进行对比分析和计算，即得到近似最优解与最短行走路径方案。

在建立求解TSP问题仿真模型中，根据需要解决的问题和期望达到的要求，采用如下方式建模：用暂存区来模拟城市节点，每个暂存区表示一个城市；用作为临时实体的任务执行器来模拟旅行者，旅行者由一个发生器产生；用吸收器来吸收作为临时实体的旅行者，进入吸收器后，代表旅行者走完了所有的城市和一个仿真过程的结束。在仿真模型中，通过设置临时实体流的发送端口来控制旅行者的行走路线，由于每次仿真运行产生的随机数不同，每次的行走路线也不同，在仿真中记录每次的行走路线和距离，经过若干次仿真后，对仿真结果进行对比分析，找出路径最短的路线作为TSP问题的近似最优解。

2.2 仿真模型建立步骤

1）构建模型布局 根据旅行者所经过的城市，以及城市间的距离，分析各种状态变量与参数的逻辑关系，建立求解TSP问题仿真的模型布局。

2）定义模型运行流程 根据Flexsim对象实体间的逻辑层次关系，连接输入输出端口，定义运行流程，实现仿真的目的。

3）编辑实体参数 以所构建模型想要达到的仿真模拟目标，对实体对象进行参数编辑，设定各实体的标签值，以完成系统的仿真。

4）运行仿真 模型实体对象的连线完成后，编辑各实体模型运作参数，根据逻辑关系编写程序，进行仿真运行，直观的观察模型的运行情况。

5）分析仿真结果 通过对仿真模型的运行，可以得到各类的图表及统计数据，分析仿真运行结果，对仿真数据进行对比，确定最优解。

3 应用示例仿真与分析

3.1 模型案例

为考察仿真模型的有效性，以一个应用示例进行了模拟，用Flexsim软件建立仿真模型，确定一条行走路径，在经过所有城市且只经过一次的情况下使得行走距离最短。模型案例采用一个典型的TSP问题，即10个城市问题。

3.2 仿真模型建立

首先构建仿真模型的布局和连线，以暂存区表示节点城市，节点之间采用a连接，连接方式如下：发生器与10个城市(暂存区)进行a连接，10个暂存区再与吸收器进行a连接，每个暂存区再与其他9个暂存区a连接，连接好之后，每个暂存区有10个输入端口和10个输出端口，模型布局和实体间连线如图1所示。

模型需要达到的效果描述如下：首先由发生器产生一个临时实体，代表旅行者，随机到达某一个暂存区后，通过设置输出端口，控制下一站到某个暂存区，具体到哪个暂存区由程序控制，要求下一站随机选择并且不与之前到过的暂存区重复，在此过程中记录走过的暂存区并计算走过的距离，这些数据保存在全局表中，当旅行者经过最后一个节点后，进入吸收器被吸收，完成一次旅行过程的模拟。经过若干次仿真运行后，在全局表中选择一条路径最短的行走路线，作为TSP问题近似最优解。为了实现模型要达到的效果，需要进行各个实体对象的参数设置、标签设置、程序设计和结果输出等。

图1 仿真模型布局图

3.2.1 发生器、暂存区参数设置

发生器的主要作用是产生临时实体，为了比较真实地模拟旅行者行走过程，临时实体种类选择“任务执行类临时实体”，到达方式选择“到达时间间隔exponential（0，100，0）”，勾选“使用运输工具”并选择“任务执行器作为临时实体”，这样仿真运行时能显示临时实体行走过程，10个暂存区的“临时实体流”页面设置同上。

3.2.2 实体对象标签设置

为了完成仿真过程，很多变量需要借助标签值来设定，在后面的程序设计中用来完成计数、标记、计算等功能，上述标签均为数值型标签，各实体对象主要设定的标签以及所起的作用如表1所示。

表1 各实体对象标签及其作用

3.2.3 全局表建立

在模型建立和仿真运行中需要用到2个全局表，分别用来存储城市距离的原始数据和仿真结果的数据。在Flexsim中建2张表，名称分别为“gt1”和“gt2”。“gt1”如图2所示，根据城市编号组成的行和列即可读取出两城市间的距离；“gt2”用来存储仿真中旅行者走过的路径和走过的总距离，共11列，前10列存储依次走过的城市编号，最后一列存储总距离，表的行数由程序动态设定，即产生多少个临时实体就设定多少行，每一行记录的是每个临时实体走过的路径和距离。

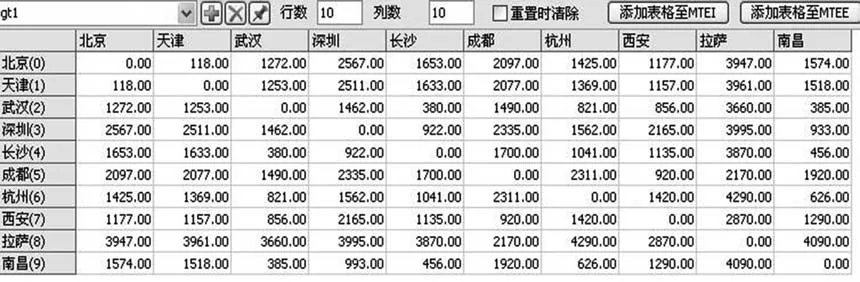
图2 存储城市数据的全局表

3.2.4 程序设计

上述步骤完成后，通过编程来确定每个实体的发送端口、计算行走距离等。

发生器产生临时实体后，需要确定发送端口。由于与10个城市相连，在“发送至端口”中，由随机数确定一个发送端口：return duniform(1,10)；在发生器中还需要完成临时实体的计数，并将计数值写入临时实体标签值中，同时设定全局表“gt2”的行数，上述操作在“离开触发”中进行；当再次运行仿真模型时，需要重置，将临时实体计数的标签值清零，并且将全局表“gt2”的行数设定为0，以便重新开始仿真，完成上述操作在“重置触发”中进行。

临时实体进入暂存区后要完成行走距离的计算，记录经过的城市，确定临时实体输出端口。

1）计算当前临时实体行走距离、记录行走路径 这一步在暂存区的“进入触发”里实现，首先获取临时实体各项标签值，主要标签变量见表3的临时实体对象，初始值均为0，判断城市计数标签值，如果为0，代表临时实体从发生器过来，为初次进入暂存区，不计算走过的距离，将城市计数加1并写入临时实体对应标签值中，在全局表中根据临时实体计数标签值和城市计数标签值确定对应的行和列，将获取的当前暂存区“city”值，即当前走过的城市写入全局表中，然后将暂存区“city”值写入临时实体标签“pecity”中，用于在下一站判断上一站所经过的城市。如果城市计数标签值大于0，则要计算走过的距离，其他操作同上，距离计算过程为：根据临时实体标签“pecity”和当前暂存区标签“city”，即根据上个城市和当前城市组成的行和列查询全局表“gt1”，获取2个城市间的距离，累加到临时实体标签“mydistan”中，并将计算后的值写入标签中用于下一站累加计算，当走完所有城市后，即可得到走过的总距离。暂存区“进入触发”算法流程描述如下：

2）确定临时实体输出端口 在暂存区的“临时实体流”属性页面中设置“发送至端口”来实现，当临时实体经过当前暂存区后，要控制其进入下一个暂存区，在此过程中，要求临时实体随机选择下一个暂存区，并且不与之前经过的暂存区重复，具体过程为：首先获取临时实体的城市计数标签“sumci⁃ty”的值并进行判断，如果值为10，说明已经走过了所有的城市，下一步直接进入吸收器，否则，随机确定下一个输出端口，将与当前暂存区输出端口连接的其他暂存区标签值“city”与已经存入全局表的城市标签值比较，如果未存入全局表，则表示未经过此城市，存入数组中，随机产生数组长度内的随机数作为数组序号，读取数组里对应的值作为下一个要到达的城市，遍历输出端口对应的城市标签值，获得输出端口值并返回。暂存区“发送至端口”算法流程描述如下：

3.3 仿真实验结果及其分析

仿真实例选取自TSPlib测试库，仿真实验环境为Flexsim7.5中文版仿真软件，模型建立完成以及参数设置好之后，对仿真模型运行以获取仿真结果，临时实体行走路线完全由暂存区的输出端口确定，而输出端口都由随机数确定，产生的随机数不同，则行走路线和行走的总距离就不一样，仿真的目的就是要找出一条行走距离最短的路线，仿真模型运行时不断地产生临时实体，每个临时实体走完全部城市进入吸收器后即完成一次旅行，记录每次旅行的计算结果，通过对计算结果的比较来找出距离最短的行走路线以及走过的距离。

1）获取行走路径信息及最短路径 建立全局表“gt3”，存储路径最短临时实体经过的城市以及总距离信息，1行11列，临时实体经过所有的暂存区后，进入吸收器，在吸收器“进入触发”中完成如下操作，从临时实体标签值中获取行走总距离信息写入吸收器“mydistan”标签，并写入全局表对应行的最后一列中。另外还需要记录仿真过程中最短路径，如果是第一个临时实体进入吸收器，将当前路径总距离写入“mindistan”，否则比较两者大小，如果小于之前记录的最短路径，则将当前路径总距离写入“mindistan”标签，并将经过的路径和总距离写入全局表“gt3”，算法流程描述如下：

2）图表数据输出 在仿真中需要以曲线图实时显示每个临时实体走过总距离的情况，用Flex⁃sim自带的绘图功能实现，在属性设置中，选择统计的实体为吸收器，统计的变量为吸收器标签“mydistan”，再设置曲线颜色，横坐标纵坐标等参数，在仿真中即可显示行走总距离的曲线，最短路径搜索曲线，以查看最短路径搜索情况。

3）运行仿真模型及获取仿真结果 所有程序、参数调试完成后可仿真运行，为尽可能搜寻到最优解，仿真终止时间设置为2 000 s，运行结果存储在全局表中，显示每次行走的路径及总距离，曲线在仿真过程中实时显示，仿真结果及图像如图3～4所示。从图4中可以看出：此方法能对所有可行的行走路线进行搜索，只要运行次数足够，就能找出最短行走距离。上述显示的是所有可行的运输方式，从中选择总成本最小的一行，即得到TSP问题仿真优化的结果，并解读出对应的行走路径和最短距离。对于本仿真实例，经过反复多次运行，确定的最短距离行走路径如图5所示，即总距离最小的行走方案为“深圳（4）-北京（1）-天津（2）-西安（8）-杭州（7）-南昌（10）-长沙（5）-武汉（3）-成都（6）-拉萨（9）”，最短距离为10 384 km。

图3 总距离曲线

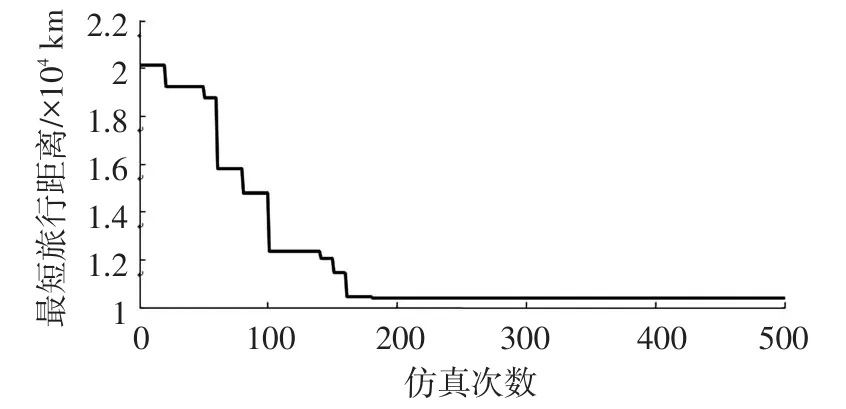
图4 最短距离变化图像

图5 最短距离及路径信息

为检验此方法求解复杂TSP问题的效果，从TSPLIB 测试库中选取了 pr136、kroB100、pr144、kroB150、CHC144等规模比较大的几个TSP问题进行了测试，按照上述过程用Flexsim仿真软件进行建模，参数设置，运行并得到仿真结果，与文献记录的最优解进行对比，测试结果如表2所示。从表2的对比结果可以看出：该仿真方法求解复杂TSP问题所求最短路径基本在文献记录的最优值附近，反映了文中方法求解TSP问题是有效的。

为更好地说明其有效性，将此方法和一些智能计算方法的求解过程和结果进行了比较。由于在Flexsim中可以任意调整仿真模型运行速度，不能以运行时间作为比较依据，为客观地比较几种算法的性能，选取平均迭代次数、求解到最优值的最少迭代次数和求解平均值进行性能比较。与模拟退火算法（SA）以及文献提出的SFCPGA［2］、SECPSO［4］、GFOA［5］算法对比结果如表3所示。从表3可以看出：在迭代次数较少的情况下，Flexsim仿真算法的性能优于或接近所列出的对比算法，从而进一步验证了算法的有效性。

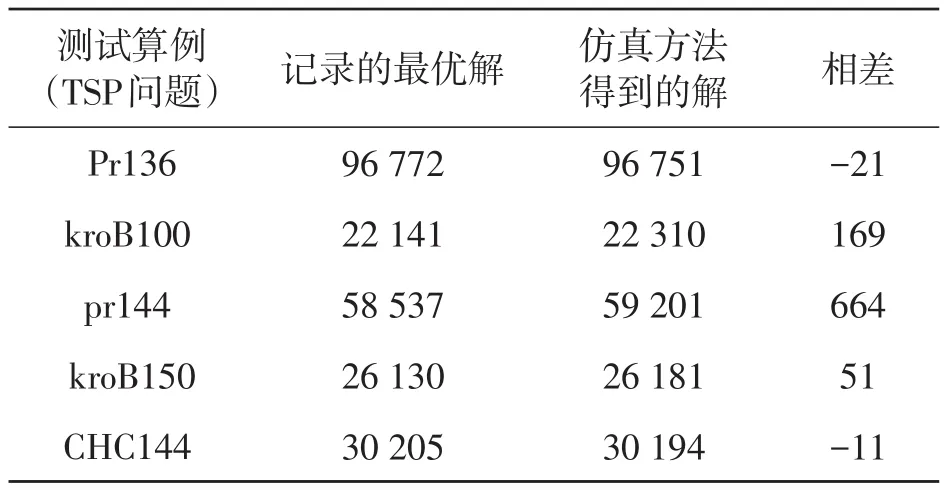
表2 文中方法对复杂TSP问题的求解结果

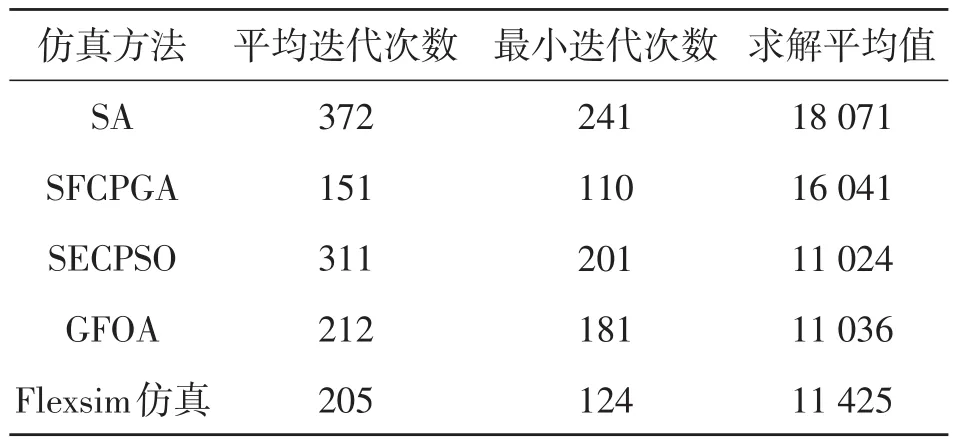
表3 文中方法和智能算法的比较

4 结束语

在分析了TSP问题求解特点的基础上，用Flexsim软件进行了建模，解决了参数设置、仿真模拟、结果输出等环节中的问题，通过仿真寻找到了满足距离最短的路径，证明了文中方法的可行性和有效性。与其他基于智能计算的优化方法相比，此方法建模快速，运行结果可靠，不会产生如进化计算中交叉变异后的不可行解，避免了复杂的编程计算以及陷入局部解的问题，实现了优化过程的可视化，对典型TSP问题仿真实验表明了此方法的实用性。文中只针对求解最短路径及最短距离进行了建模，仿真中路径随机产生，基本类似穷举法，没有考虑采用启发式算子来引导搜索以便更快地找到最优解。如何进一步改进该模型，使其用于更复杂的TSP问题求解，将是下一步工作的研究重点。

［1］殷旅江，何波，杨立君.多类指派约束下汽车总装装配线平衡优化［J］.制造业自动化，2014，36（24）：41-44.

［2］许智宏，赵嘉伟，董永峰，等.基于Spark的并行遗传算法在旅行商问题中的应用［J］.计算机应用研究，2016，33（8）：45-48.

［3］牟衔臣等.基于遗传算法航路规划TSP问题的研究［J］.系统仿真学报，2013，25（8）：86-89.

［4］程毕芸，鲁海燕，黄洋，等.求解TSP的自适应优秀系数粒子群优化算法［J］.计算机应用，2017，37（3）：750-754+781.

［5］段艳明，肖辉辉.求解TSP问题的改进果蝇优化算法［J］.计算机工程与应用，2016，52（6）：144-149.

［6］Yin L,Li X,Gao L,et al.A New Improved Fruit Fly Opti⁃mization Algorithm for Traveling Salesman Problem［C］//Eighth International Conference on Advanced Computa⁃tional Intelligence.IEEE,2016:21-28.

［7］孟巧凤，张林鍹，董杰涛，等.基于Flexsim仿真的装配线平衡方法研究［J］.计算机仿真，2016，33（6）：176-179.

［8］王聪，张宏立.文化基因算法求解TSP问题的研究［J］.计算机仿真，2015，32（2）：284-287+358.

Research on Flexsim Simulation Method for Solving TSP Problem

Zhang Weifeng
（School of Economics and Management,Hubei University of Automotive Technology,Shiyan 442002,China）

TSP problem is a typical combinatorial optimization problem,the general intelligent optimiza⁃tion algorithm has the difficulty of solving the problem and it is easy to fall into the local solution.A method with Flexsim simulation software was proposed.Taking the shortest distance as the optimization objective,the Flexsim simulation model was established,and the optimal travel scheme was determined by simulation.The simulation results show that this method is effective and can solve the travel path planning problem better.

TSP;route optimization;simulation;Flexsim

TP301.6

A

1008-5483（2017）04-0075-06

10.3969/j.issn.1008-5483.2017.04.017

2017-05-24

张伟丰（1978-），男，湖北天门人，硕士，从事数据挖掘与智能计算方面的研究。E-mail：zhangweifeng7708@163.com