光伏电池的工程实用建模及仿真

党存禄 ，李建华 ，陈维铅 ，杜 巍 ，林 莉

（1.兰州理工大学 电气工程与信息工程学院，兰州 730050；2.甘肃省太阳能发电系统工程重点实验室，酒泉 735000）

光伏电池的工程实用建模及仿真

党存禄1，李建华1，陈维铅2，杜 巍1，林 莉2

（1.兰州理工大学 电气工程与信息工程学院，兰州 730050；2.甘肃省太阳能发电系统工程重点实验室，酒泉 735000）

通过分析光伏电池的物理特性，为更好地研究温度、光照强度等外界环境对光伏电池输出功率的影响，该文提出了一种适用于工程实用的光伏电池简化数学模型。在Matalb仿真平台上建立了该工程实用模型，在不同温度和光照强度下进行仿真研究。仿真结果表明，该实用模型能准确地反映光伏电池的输出特性，为下一步研究光伏发电系统提供了可靠的仿真电源。

光伏电池；物理特性；工程实用；Matalb仿真

为缓解能源危机和环境恶化，发展可再生能源是解决能源问题的途径之一[1]。太阳能作为一种可再生能源，取之不尽，用之不竭，而且清洁无污染，是世界公认的绿色能源[2]。单个光伏电池因其带电量太小而不能满足实际应用，所谓光伏列阵是将诸多光伏电池通过串联或并联组合，从而使其输出电压和电流达到需求[3]。

光伏电池具有强烈的非线性[4]，不能通过电压源或者电流源对其进行建模仿真。近年来，许多学者对光伏电池的建模进行了研究，这些模型主要分为基于光伏电池的输出特性、根据光伏电池的物理机制建模、将光伏电池等效为一个电压源[4]。这些建模方法主要针对一些特定的情况，缺乏通用性，且过于理想化，不适于工程应用。在此，提出了一种适用于工程实际的光伏电池简化数学模型，该模型利用生产厂家给出的4个技术参数，并结合当时的环境变化计算出相对应的补偿系数，最后通过Matalb/Simulink仿真平台进行验证。

1 光伏电池的数学模型

光伏电池的结构类似于一个P-N结，其特性与二极管相似。根据光伏电池的内部结构，可得到它的等效电路[5]，如图1所示。

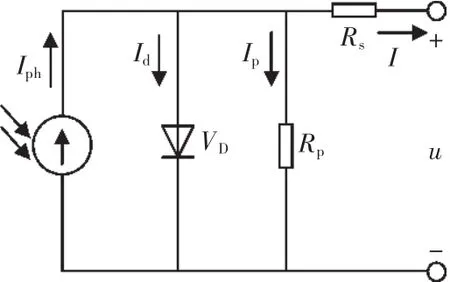
图1 光伏电池等效电路Fig.1 Equivalent circuit of photovoltaic cell

式中：I为光伏电池的输出电流；Iph为光生电流；I0为二极管反向饱和电流；q为单位电荷量，q=1.602×10-19C；U为输出电压；Rs为等效串联电阻；n为二极管理想因子，取值n=1～2；k为玻尔兹曼常量，k=1.381×10-23J/K；T为电池温度；Rp为等效并联电阻。

式（1）为光伏电池最基本的数学表达式，反映了其I-U关系，已被大家广泛认可，并应用到光伏电池理论分析研究中。 但是，该式中的参数（Iph，I0，T，Rs，Rp）与电池温度和光照强度关系密切，难以计算出准确数值，生产厂家也不提供，因此式（1）不适用于工程建模。

由基尔霍夫电流定律可知光伏电池的I-U特性方程为

2 光伏电池工程实用模型

在实际工程中，生产厂家仅提供标准条件（温度25℃，光照强度1000 W/m2）下，光伏电池的开路电压Uoc、短路电流Isc、最大功率点电压Um及最大功率点电流Im等基本参数。为了能够利用这些基本参数对光伏电池进行建模仿真，需要对其做进一步简化，忽略一些对输出电流影响很小的因素，采用厂家提供的参数计算出剩余的物理参数。

因串联电阻Rp非常大，串联电阻Rs非常小[6]，对光伏电池输出电流的影响很小，常常忽略（U+Rs）/Rp项，则式（1）简化为

当光伏电池短路即Isc=Iph，U=0时，Rs远小于二极管正向导通电阻，故可以忽略流经二极管的电流Id，此时 Isc=Iph。

在标准条件下，将光伏电池的数学模型简化为

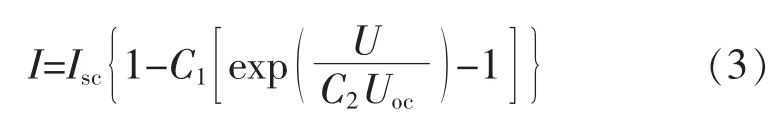
在最大功率点（I=Im，U=Um）处，

一般情况下，

代入式（4），可求得 C1为

在光伏电池开路即 I=0，U=Uoc时，将式（5）代入式（4），可求得 C2为

因此，利用光伏厂商所提供的4个基本参数便可根据式（5）和式（6）求出 C1，C2，再将其代入式（3），可得到光伏电池的I-U方程。

3 温度和光强变化情况下的工用模型

光伏电池的I-U特性曲线与温度和光照强度紧密相关[7]。在温度和光照强度变化情况下，根据厂家提供的标况下4个基本参数，通过加入修正补偿系数，利用式（7）～式（12）可求出光伏电池在任意温度和光照强度下的参数（Isc_n，Im_n，Usc_n，Um_n），然后将这 4 个参数代入式（3）、式（5）和式（6），便可计算出任意温度和光照强度下的I-U特性曲线。

式中：ΔT为光伏电池的实际温度与标准温度之差；ΔS为实际光照强度与标准光照强度之差；Isc_n、Im_n、Usc_n、Um_n分别为任意温度和光照强度下的短路电流、最大工作点电流、开路电压、最大功率点电压；a，b，c为补偿系数，根据大量工程试验数据，可分别取值 a=0.0025 ℃-1，b=0.5，c=0.00288 ℃-1；e 为自然底数，取近似值。

4 光伏电池仿真

使用广州磊阳太阳能公司提供的NY-D120 WP型号光伏电池进行研究，在标准条件下的参数Isc=7.68 A、Im=6.86 A、Uoc=21.24 V、Um=17.5 V、Pm=120 W。

4.1 标准条件下光伏电池的仿真

在Simulink中搭建光伏电池的工程实用模型，如图2所示。

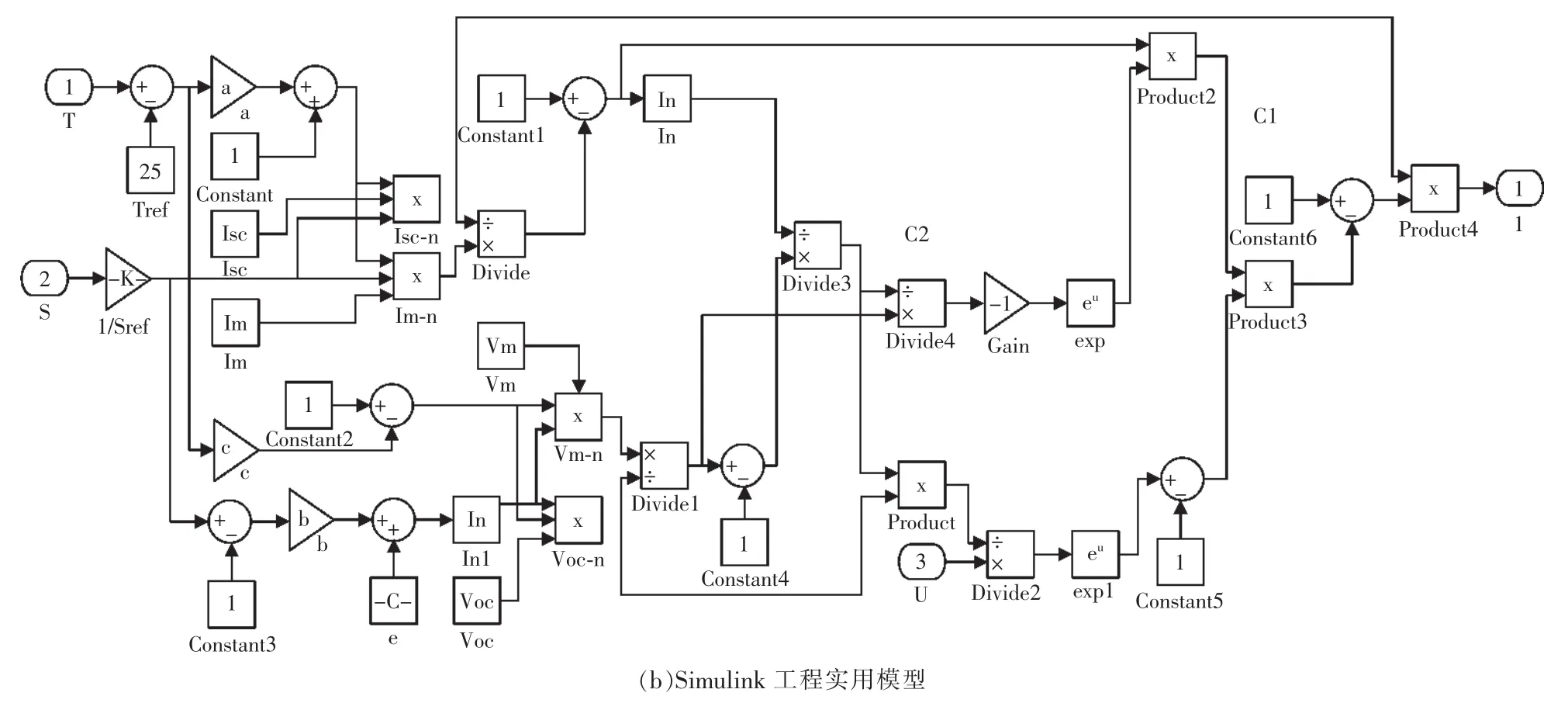
图2 光伏电池的工程实用模型及封装Fig.2 Practical engineering model and package of photovoltaic cells

在标准条件下，对光伏电池工用模型进行仿真，得到其I-U，P-U特性曲线，如图3所示。由图3（a）可知，当光伏电池的输出电压较低时，可近似视为恒流源；当输出电压较高时，可近似视为恒压源。由图3（b）可知，当温度和光照强度一定时，光伏电池只有一个最大功率点。

4.2 温度、光照强度变化时光伏电池的仿真

光伏电池的输出特性受到温度和光照强度的影响。当温度为25℃，光照强度变化时，对实用模型进行仿真，得到光伏电池的I-U，P-U特性曲线，如图4所示。当光照强度为1000 W/m2，温度变化时，得到光伏电池的I-U，P-U特性曲线，如图5所示。

图3光伏电池的I-U、P-U特性曲线Fig.3 I-U，P-U characteristic curve of photovoltaic cells

由图4（a）可知，温度一定时，随着光照强度的增加，光伏电池的短路电流也随之增加，开路电压增加的幅度较小；由图4（b）可知，光伏电池输出的最大功率随光照强度的增加而增加，且幅度较为明显。

图4 温度一定，光照强度变化时光伏电池I-U、P-U特性曲线Fig.4 I-U，P-U characteristic curves of photovoltaic cells with certain temperature and varying light intensity

图5 光照强度一定，温度变化时光伏电池I-U、P-U特性曲线Fig.5 I-U，P-U characteristic curves of photovoltaic cells with certain light intensity and varying temperature

由图5（a）可知，光照强度一定时，随着温度的升高，光伏电池的开路电压也随之减小，短路电流缺略有增加；由图5（b）可知，光伏电池输出的最大功率随温度的增加而略微减小，且在最大功率点处的电压值也逐渐变小。

由上述仿真结果图可知，光伏电池是一个非线性电源，其输出特性与温度和光照强度的变化紧密相关，当温度和光照强度一定时，光伏电池只有一个最大功率点。光照强度的变化对光伏电池输出功率的影响比温度变化的影响大。

为进一步研究光伏电池工用模型的有效性和适用性，定义光伏电池的输出电压、输出电流和输出功率的相对误差分别为

式中：Ia，Ua，Pa分别为光伏电池工用模型的仿真结果；Ib，Ub，Pm分别为 NY-D120WP 型号光伏电池的基本参数。将基本参数、仿真结果及相对误差绘制成误差分析表，如表1所示。

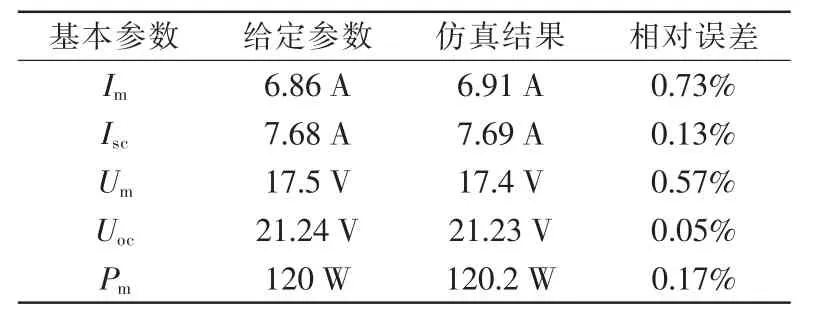
表1 误差分析表Tab.1 Error analysis

由表1可知，用光伏电池工程实用模型仿真的结果与厂家给出的基本参数之间的相对误差很小，能够很好的对电池进行仿真，进一步证明了该模型的合理性。

5 结语

对光伏电池的数学模型进行了简化，并通过引入工程修正补偿系数，得出了一种适用于工程实际的光伏电池简化数学模型，在Simulink仿真环境中搭建了工程实用模型。仿真结果表明，该实用模型是可行的、有效的，能准确反映环境和光照强度变化时光伏电池的输出特性，为进一步追踪最大功率点及光伏发电系统提供了良好的仿真电源。

[1] 杨晶惠，庹先国，吕中云，等.光伏发电系统最大功率跟踪控制器的实现[J].自动化与仪表，2016，31（2）：17-21.

[2] 冷淼，徐婷.基于MATLAB/SIMULINK的光伏电池建模与仿真分析[J].山东工业技术，2016，12（16）：234-235.

[3] 王欢，徐小力，赵文祥.物联网架构的光伏自跟踪发电监控系统设计[J].自动化与仪表，2015，30（12）：6-10.

[4] 张纯杰，赵志刚，桑虎堂.光伏电池的建模综述[J].电源技术，2016，40（4）：927-930.

[5] 曹龙汉，余佳玲，李景南，等.基于MATLAB/Simulink的光伏电池仿真建模研究[J].半导体光电，2015，40（5）：718-721.

[6] 郭天勇，陈晨.光伏并网发电系统的虚拟平台设计[J].自动化与仪表，2015，30（10）：66-69.

[7] 王竞超，汪友华.光伏电池的建模和仿真[J].电源技术，2012，36（9）：1303-1305.

Engineering Practical Modeling and Simulation of Photovoltaic Cells

DANG Cun-lu1，LI Jian-hua1，CHEN Wei-qian2，DU Wei1，LIN Li2
（1.School of Electrical and Information Engineering，Lanzhou University of Technology，Lanzhou 730050，China；2.Gansu Provincial Key Laboratory of Solar Power System Engineering，Jiuquan 735000，China）

By analyzing the physical characteristics of photovoltaic cells，in order to study the influence of temperature，light intensity and other external environment on the output power of photovoltaic cells，a simplified mathematical model for photovoltaic cells is proposed.The practical model of the project is built on the Matalb simulation platform，and the simulation is carried out under different temperature and illumination intensity.The simulation results show that the practical model can accurately reflect the output characteristics of photovoltaic cells，and provide a reliable simulation power for the next study of photovoltaic power generation system.

photovoltaic cell；physical characteristics；practical engineering；Matlab simulation

TP273；TM615

A

1001-9944（2017）08-0005-04

10.19557/j.cnki.1001-9944.2017.08.002

2017-04-06；

2017-06-11

甘肃省教育厅高校科研项目（2015A-211）；甘肃省科技计划项目（1309RTSF043）

党存禄（1964—），男，本科，教授，研究方向为新能源发电技术、电力电子与电力传动；李建华（1992—），男，硕士研究生，研究方向为光伏发电。