福州市土壤铬含量高光谱预测的GWR模型研究

江振蓝,杨玉盛,沙晋明,*

1 福建师范大学地理科学学院,地理学博士后科研流动站, 福州 350007 2 闽江学院地理科学系,福州 350108

福州市土壤铬含量高光谱预测的GWR模型研究

江振蓝1,2,杨玉盛1,沙晋明1,*

1 福建师范大学地理科学学院,地理学博士后科研流动站, 福州 350007 2 闽江学院地理科学系,福州 350108

通过系统分析不同光谱分辨率和光谱变换对土壤铬高光谱预测模型的不确定性影响,筛选出最优的光谱分辨率及光谱变量进行土壤铬含量预测的地理权重回归(GWR)模型构建,利用该模型进行福州市土壤铬含量预测,并将预测结果与普通最小二乘法回归(OLS)结果进行比较分析,探讨GWR模型在土壤铬高光谱预测中的适用性及局限性。结果表明：(1)在10 nm分辨率尺度下,以土壤全铬含量为因变量,反射率的二阶微分和反射率倒数的二阶微分为自变量构建的GWR模型对土壤铬预测的效果最好。GWR模型的R2和调节R2分别为0.821和0.716,较OLS模型分别提高了0.529和0.450,而AIC值为720.703,较OLS模型减少了22个单位,残差平方和仅为OLS模型的1/4,说明GWR模型的预测效果较OLS模型有了显著提高。(2)土壤铬预测模型的精度受光谱分辨率影响。对于OLS预测模型来说,3 nm分辨率的模型预测效果最好,而对于GWR预测模型来说,10 nm分辨率的模型不仅预测效果最好,其相较于OLS模型的改善作用显著,为土壤铬含量GWR预测的最佳光谱分辨率。(3)光谱的一阶微分变换可以有效增强土壤铬的光谱特征,而其余的光谱变换对土壤铬的光谱特征则未起到增强作用,但可以很好地提高模型的预测效果。(4)研究得出土壤铬GWR模型预测的最佳光谱分辨率为10 nm,为EO- 1 Hyperion影像的光谱分辨率,而且随着采样点的增加,GWR模型的预测效果趋于稳定,适合空间异质性大的区域尺度土壤铬预测。故该模型与高光谱影像结合,实现模型从实验室尺度向区域尺度的推广,为格网尺度土壤铬的空间预测提供可能。

土壤重金属铬；GWR模型；高光谱；光谱分辨率；光谱变换

重金属污染已成为当今土壤污染中污染面积最广、危害最大的环境问题之一[1- 4]。铬元素是国际社会公认的3种致癌金属之一,近年来,随铬盐、皮革、印染、电镀等涉铬工业的发展以及污水灌溉的影响,土壤铬污染日益严重[5- 8],铬已成为土壤的“优先监测污染物”之一[9]。传统的土壤重金属铬污染调查主要基于野外实地采样,实验室化学分析的方法,这些方法不仅费时费力,且仅适用于小尺度监测,无法满足土壤铬空间信息快速获取的要求。高光谱遥感技术由于能同时获得精细的几乎连续的光谱,从而能够根据地物的光谱特征对地物进行反演和识别,为快速获取土壤铬信息提供了可能[10- 12]。土壤铬高光谱预测的机理在于高光谱遥感以其获取的连续、精细的反射光谱有可能捕捉到铬元素的光谱吸收特征,通过分析土壤铬的可见光-近红外、中红外等波段的光谱特征,选择土壤铬响应的敏感波段,从而构建模型对土壤铬进行定量预测。

目前,用于土壤铬高光谱预测的模型主要有单变量回归模型[13-15]、多元线性回归模型[16-19]、主成分回归法[18]、偏最小二乘法[13,17,20-23]等。其中,偏最小二乘回归法提供了一种多对多线性回归建模的方法,能够在波段个数较大且存在严重自相关的情况下进行回归模型建模,较好地解决了单变量回归模型信息利用不全及多元线性回归面临的多重共线性问题,已成为土壤重金属铬高光谱预测应用最广的模型[24]。前人构建模型的前提是空间平稳性,即假定研究区内土壤重金属含量与光谱反射率的相关关系在研究区内是相同的,模型系数在研究区内是不变的。然而,土壤光谱特征是土壤有关性质的综合反映,土壤并非一个均质体,而是一个时空连续的变异体,土壤重金属含量的空间分布非常复杂,受成土母质、高程、土地利用方式、工业布局、路网、污水灌溉等因素的影响,具有高度的空间异质性[25-33]。而且除重金属外,土壤光谱还受到土壤结构和成分、植被等环境变量影响,故在不同的研究区域,不同的位置,由于土壤类型、组分和污染水平不同,土壤重金属含量与光谱特征的关系也将发生变化,前人构建模型的空间平稳性前提与实际情况不相吻合,使得不同研究区所得结论有可能是不同的。如Dong等[23]利用偏最小二乘法进行苹果园土壤的重金属预测研究中认为,与土壤有机质、PH值相关性较强的Cu和Zn元素预测效果要好于Pb和Cr元素,而Wu等[11]利用偏最小二乘法对南京郊区土壤重金属预测中发现亲Fe重金属Ni,Cu,Cr和Hg的预测精度高于Pb,Zn和As元素,Song等[21]在对农业土壤重金属预测研究则得出与土壤氧化铁、粘土、有机质含量相关性较强的Cr、Cu和As元素的预测效果要好于Cd、Pb和Hg元素。故前人构建的土壤铬高光谱模型由于忽视土壤铬与光谱特征关系的空间非平稳性,虽然在各自的研究区取得了较好的结果,却很难在其他区域推广。

地理权重回归(Geographically Weighted Regression, GWR)模型[34],采用局部估计回归模型,其核心思路是采样点对其附近点的特征的影响要大于离其较远的点,点位的回归系数不再是利用全局信息获得,而是利用邻近观测值的样本数据进行局部回归估计得到的。该方法克服了普通多元回归方法的缺点,它将数据的空间位置嵌入到回归参数中,使得对空间估值问题更合乎实际[35- 38]。本文将地理权重回归模型引入到土壤重金属铬的高光谱预测中,并通过分析不同光谱分辨率及光谱变换对模型构建的不确定性影响,筛选出最优光谱分辨率及光谱变换方法,构建有效的土壤铬的GWR预测模型,为GWR模型在土壤铬高光谱预测中的应用提供理论依据。

1 数据来源及其处理

1.1 土壤样品采集和分析

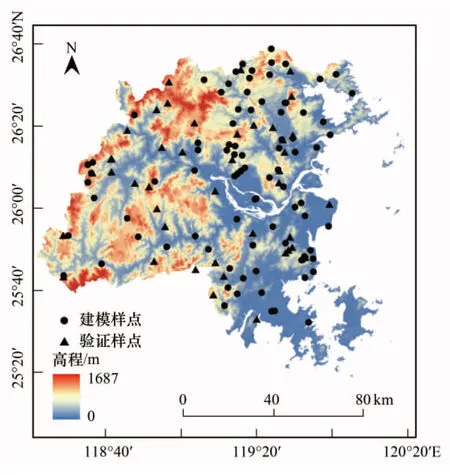
图1 研究区与采样点分布Fig.1 Study area and sample sites

福州市位于我国东南沿海,东经118°08′— 120°31′,北纬25°15′—26°29′,全区面积为11968km2。属于亚热带海洋性季风气候,年均温在16—20℃,年降水量为900—1200 mm。境内多山,濒临海洋,地势自东向西倾斜,地形起伏大,成土条件复杂。土壤类型主要有赤红壤、红壤、黄壤及水稻土等,呈酸性。本研究在福州市(除平潭县外),约11597 km2范围内采集土壤样本。样点布设主要是以环境保护部和中国科学院于2012年1月启动的“全国生态环境十年变化(2000—2010年)遥感调查与评估”项目布设的福建省野外核查点为基础进行的,核查点主要由项目组采用分层抽样方法进行统一布设,分层抽样第一层次为全国,第二层为植被气候分区。样本的各区分配以土地覆盖图斑密度为依据,以空间随机分布为原则分配空间位置,在福建省共布设1317个核查点,其中160个布设在福州市。本项目根据核查点可到达程度和采样的可行性,并结合福州市的地形特征、土地覆盖类型及各地类相应的面积,确保研究区内具有代表性的地类均有重复采样点布设的前提下,共采集131个0—20 cm土壤表层土样,并利用GPS记录高程,样点分布较为均匀(图1)。样点包含红壤、黄壤、赤红壤、水稻土等土壤类型,并涵盖了林地、草地、耕地、建设用地、裸露地等土地覆盖类型。每个采样点混合后取500 g土样,经实验室风干,去除沙砾及动植物残体后,研磨,过100目尼龙筛。每个样品分成两份,一份用来进行化学分析,另一份用来进行光谱分析。土壤全铬含量采用电感耦合等离子质谱(ICP-MS,美国Thermo Electron)进行测定。

1.2 土壤光谱测定及其预处理

土壤样品光谱测定采用美国ASD(Analytical Spectral Device)公司生产的地物光谱仪FieldSpec 3在室内测量,以 1000 W的卤光灯为光源,采用15°的光源照射角度、15 cm的探头距离及30 cm的光源距离,从垂直于土壤表面的方向进行土壤反射光谱测量,并利用40 cm×40 cm的白板进行定标,获取绝对反射率。该光谱仪波段范围为350—2500 nm,在350—1100 nm和1000—2500 nm范围内的光谱采样间隔分别为1.4 nm和2 nm,光谱重采样后的间隔为1 nm,输出2151个波段。每个土样采集10条光谱曲线,利用ViewSpec Pro软件剔除异常曲线后取光谱反射率平均值作为样本的原始反射率光谱值[15]。光谱预处理主要包括：1) 利用Savitzky-Golay平滑对曲线进行处理,以消除光谱曲线上存在的“毛刺”噪声；2)对平滑后的数据分别以1、2、3、4、5、6、7、8、9、10 nm进行算术平均运算进行重采样,分别获得1、2、3、4、5、6、7、8、9、10 nm光谱分辨率的土壤光谱反射率,以分析不同光谱分辨率对模型构建的影响。

1.3 土壤光谱变换与特征波段选取

为有效消除背景噪声,突出光谱的特征值,本文对光谱反射率(Spectral Reflectance, SR)进行以下变换：一阶微分(First Derivative, FD)、二阶微分(Second Derivative, SD)、倒数变换(Reciprocal Transformation, RT)、倒数的一阶微分(RTFD)、倒数的二阶微分(RTSD)、倒数对数变换(吸光率,Absorbance Transform,AT)、倒数对数的一阶微分(ATFD)、倒数对数的二阶微分(ATSD)及连续统去除(Continuum Removal, CR)等。利用土壤全铬含量与变换后的光谱数据进行相关分析,筛选出相关系数最大的光谱特征波段。在不同光谱分辨率尺度下,以全铬含量为因变量,各光谱特征值为自变量,通过逐步回归分析方法,筛选出共线性小的变量参与模型的构建。

2 GWR模型

GWR是由Fotheringham等[34]提出的一个空间变参数模型,是对普通最小二乘法回归(Ordinary Least Squares Regression, OLS)模型(式1)的空间扩展,将数据的地理位置嵌入到回归参数之中,使得参数可以进行局部估计,扩展后的模型如式2。

(1)

(2)

式中,yi为样点i的因变量,xik为第i个样点上第k个变量的观测值,(ui,vi)为样点i的地理空间坐标,β0(μi,νi)为回归的常数项,βk(ui,vi)为第i个采样点上的第k个回归参数,εi为误差项。如果βk(u,v)在空间保持不变,则模型(式2)就变为全局模型(式1)。

GWR模型中的βk(ui,vi)参数估算采用加权最小二乘法实现,用矩阵形式表示为：

(3)

式中,W(μi,νi)为m×m的空间权重矩阵,X为m×(n+1)自变量矩阵,Y为m×1因变量矩阵。故GWR模型中参数的估算关键在于空间权重矩阵的估算,本文采用高斯函数来实现(式(4))。

(4)

式中,Wij为由已知点j估计待测点i时的权重,dij为估算点i与样点j间的欧氏距离,h为带宽。其中带宽h由最小AIC信息准则(Akaike Information Criterion)确定。本文的GWR回归过程在Fotheringham等人开发的GWR 3.0软件支持下完成,模型精度评价采用AIC准则、调节决定系数(AdjustedR2)、残差平方和(RSS)等指标进行评价。此外,铬的预测值与实测值间的相关系数(R)也被用来比较GWR与OLS的预测效果。

3 结果与讨论

3.1 土壤全铬含量的统计分析

研究区土壤全铬含量在0.75—111.55 mg/kg之间,平均值为26.13 mg/kg,标准差为17.85 mg/kg。土样全铬含量变化幅度较大,变异系数为68.31%,在空间分布上呈现出较强的异质性特点,用于建模具有较好的代表性。研究区全铬含量,除处于罗源的一个样本超过国家一级标准自然背景值外[39],其他样本均未超标,且其平均值低于福建省土壤背景值(41.3 mg/kg)[40],基本上可代表福州市土壤铬元素背景值,其研究结果可为区域土壤铬元素含量背景值调查提供参考。

3.2 土壤铬含量预测的敏感光谱波段

在不同光谱分辨率尺度下,经变换后的光谱值与全铬含量进行Pearson相关分析,筛选出最大相关系数及其对应的光谱特征波段(表1)。

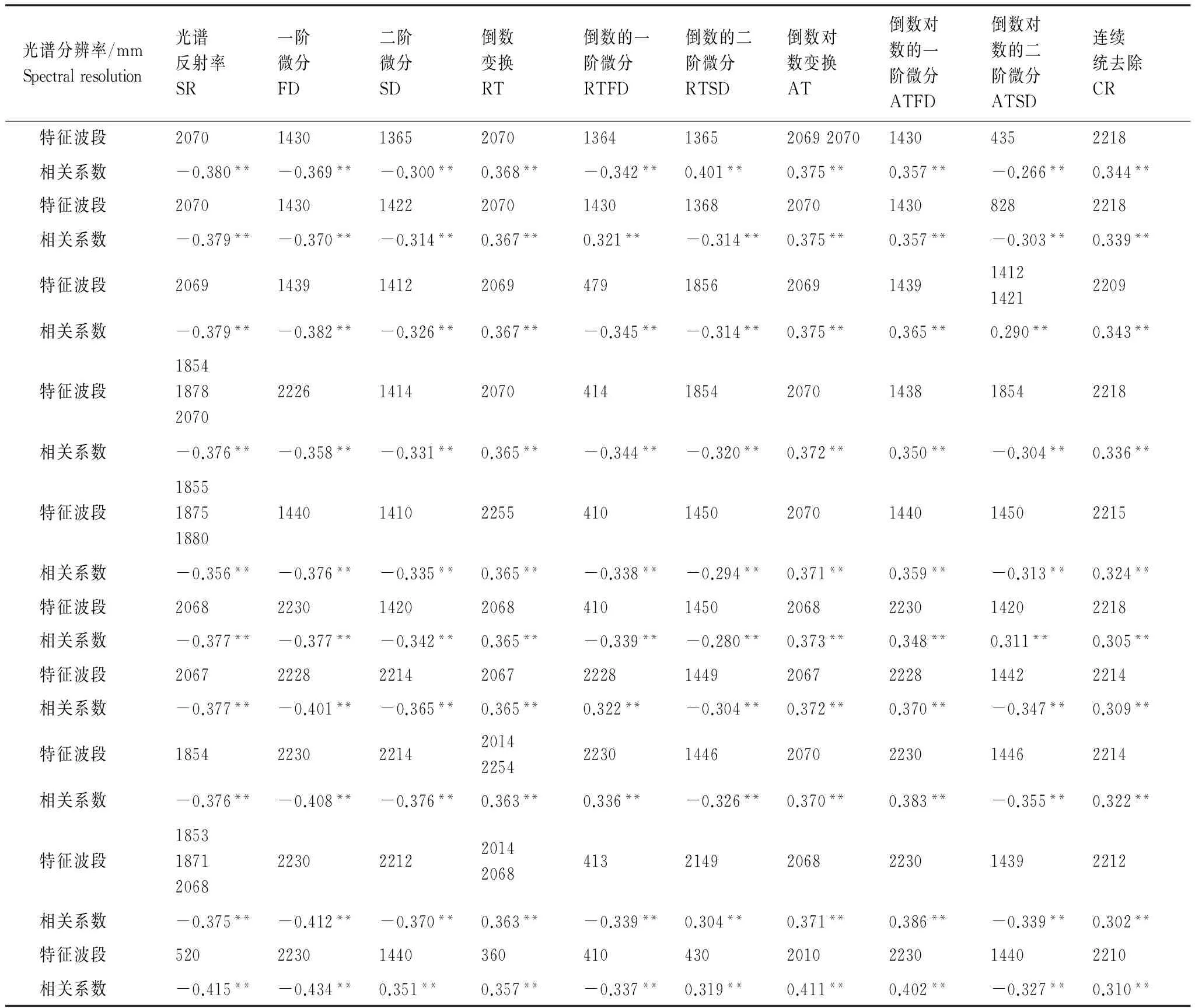
表1 福州市土壤铬与变换光谱最大相关系数的特征波段

**表示在0.01水平(双侧)上极显著相关

由表1可知,各变换光谱与土壤铬的最大相关系数在不同光谱分辨率尺度下均达到0.01极显著相关水平。土壤铬的光谱特征波段主要位于可见光410—430 nm附近(氧化铁的吸收波段),近红外的1400 nm以及1900—2250 nm附近(黏土矿物和有机质的敏感波段)。分别对全铬含量与有机质和铁含量进行Pearson相关分析,土壤铬与有机质、铁含量的相关系数分别为0.221和0.209,均呈0.01水平的极显著相关,说明研究区有机质和氧化铁对土壤铬的影响均存在。但随着光谱分辨率的变化,最大相关系数不同,其所对应的特征波段也不尽相同。对于不同光谱变换来说,光谱的一阶微分变换对土壤铬的光谱特征具有较为明显的增强作用,表现为除2 nm和3 nm分辨率尺度外,一阶微分变换光谱值与土壤铬的最大相关系数均大于原始反射率与铬的最大相关系数。而其余的光谱变换对土壤铬的光谱特征则未起到增强作用,它们与土壤铬的最大相关系数均小于原始反射率与铬的最大相关系数。这与前人的研究结果基本是一致的[14,18- 19,40]。

为消除光谱变量间的多重共线性,以土壤全铬含量为因变量,特征波段的光谱值为自变量,利用逐步线性回归分析筛选出模型的光谱变量因子,筛选的标准以回归结果的R2和调节R2最大,自变量间的方差膨胀因子(Variance inflation factor, VIF)小于7.5[42]为准,结果如表2所示。

表2 利用光谱变量对土壤铬进行逐步线性回归的结果

由表2可知,随着光谱分辨率的降低,参与模型的变量个数呈递减趋势(由1 nm—4 nm分辨率的4个减少到6 nm—10 nm的2个)。不同光谱变换对不同光谱分辨率模型构建的作用也不尽相同,即在不同光谱分辨率尺度下,参与模型预测的光谱变量是不同的,但相近光谱分辨率预测模型的光谱变量却较为相近,且以变换后的光谱特征变量为主,如1和2 nm 的预测模型均有RTSD,ATSD,CR的参与,3和4 nm的预测模型均有RTFD,RTSD,CR的参与,6和7 nm预测模型均有FD,RTFD的参与,9和10 nm的预测模型均有SD,RTSD的参与。可见,光谱一阶微分变换可以很好地增强土壤铬的光谱特征,而其余光谱变换虽不能增强土壤铬的光谱特征,却可以很好地提高模型的预测精度。从模型预测效果来看,随着光谱分辨率的降低,模型预测效果呈现变差、变好、变差、再变好的趋势,具体表现为R2和调整R2的值由减小、增大、减小、再增大的变化趋势,而估计误差值则呈现变大、变小、变大、再变小的变化趋势。其中,效果最好的为3 nm分辨率的预测模型,随光谱分辨率降低,模型预测效果波动式下降,这与徐明星等[16]的研究结果较为一致。

3.3 土壤铬含量GWR预测的最佳光谱分辨率

不同光谱分辨率尺度下,以表2模型中的各光谱特征波段为自变量,土壤全铬含量为因变量,分别利用OLS法和GWR法对土壤全铬含量进行估算。根据模型的AIC值、R2、调节R2和RSS进行判断(表3),即效果较好的回归模型具有较小的AIC值和RSS,较大的R2、调节R2,以此确定土壤铬含量GWR预测的最佳光谱分辨率。

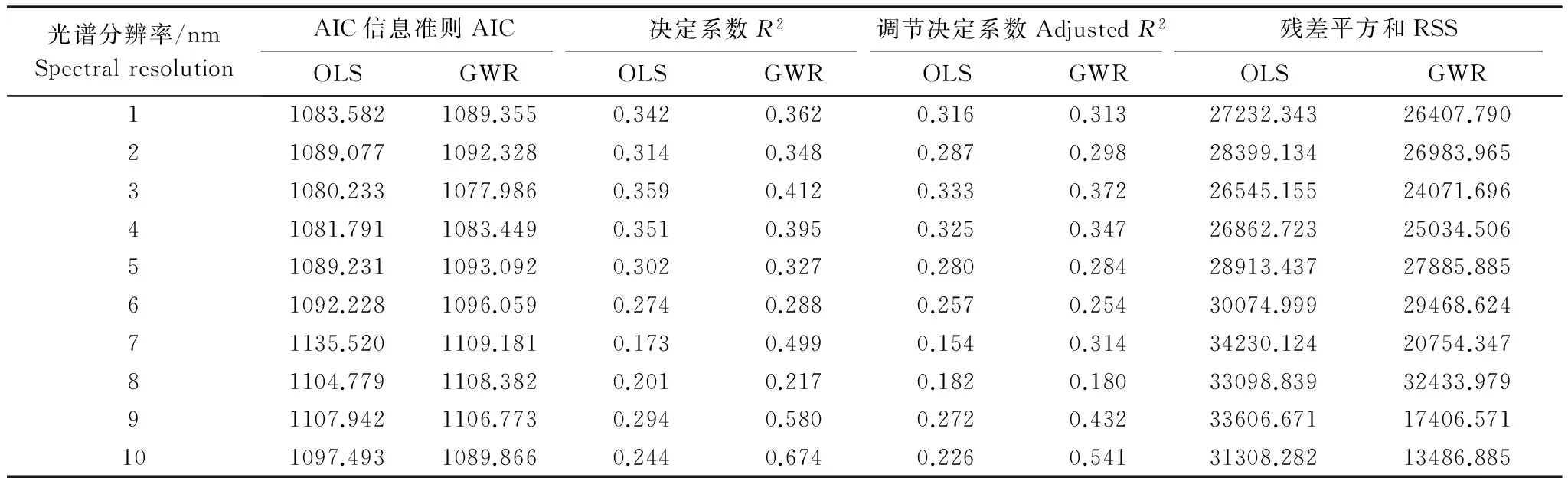
表3 不同光谱分辨率的OLS法和GWR法的模型参数

表3中各模型均通过P<0.05 的F检验。从表3可知,GWR预测模型中,10 nm分辨率的GWR模型预测能力最强,其后依次为 7 nm、3 nm和4 nm。光谱分辨率不同,GWR相较于OLS模型预测精度的提高程度也不同。其中,7 nm和10 nm分辨率的GWR模型较OLS模型预测效果有明显提高,具体表现为这两种光谱分辨率的GWR预测AIC值较OLS模型分别减少了26.339和7.627,均大于3(GWR模型较OLS模型的AIC值若能减少3个单位,认为模型有显著改善[43]),GWR预测的R2分别提高了0.326和0.430,调整R2则分别提高了0.160和0.315。而其他光谱分辨率的GWR模型预测效果较OLS模型则改善效果不显著。这主要是因为GWR模型的应用前提是空间非平稳性,GWR的预测能力及其对OLS模型的优化程度取决于该光谱分辨率下土壤铬与光谱变量间相关关系的空间非稳定性程度(表4)。

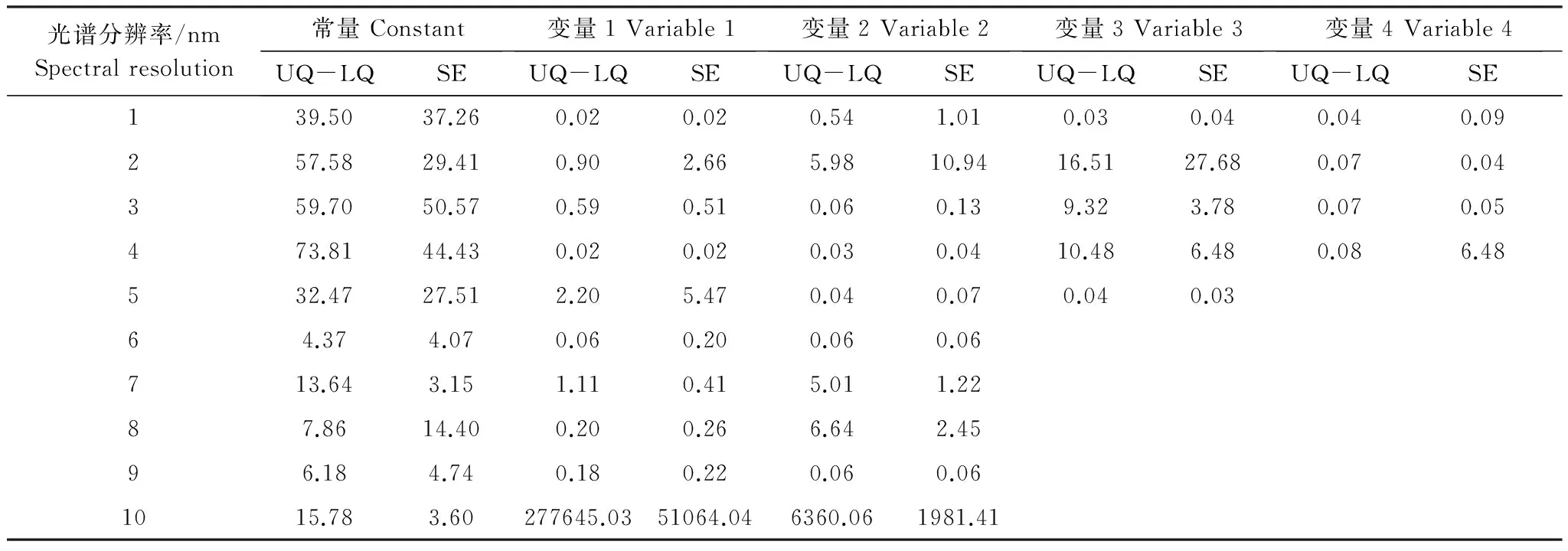
表4 福州市土壤铬与光谱变量间关系的空间非平稳性检验

表4中,当GWR模型变量参数的上四分位数(upper quartiles,UQ)与下四分位数(lower quartiles,LQ)的值范围(UQ-LQ值)大于OLS相应变量参数的两倍标准误差(standard errors,SE)时,土壤重金属与相应光谱变量的关系存在明显的空间非平稳性,反正,则空间非平稳性不明显。由表4可知,7 nm和10 nm光谱分辨率的GWR变量参数的UQ-LQ值均大于OLS相应变量参数的SE值两倍(2×SE),尤其以10 nm分辨率最为显著,其所有变量参数的UQ-LQ值甚至大于OLS相应变量参数的SE值的三倍,土壤铬与各光谱变量间关系的空间非平稳性尤为显著,故该光谱分辨率的GWR模型预测能力最强,7 nm分辨率预测模型效果次之。这也说明了较大的光谱间隔可以得到更为平滑的反射光谱曲线,在一定程度上更能充分体现土壤铬与光谱变量间关系的空间分异规律,有利于提高GWR模型的效果。然而随着光谱分辨率的降低,信息量也将随之减少,进而影响土壤铬反演精度。如何充分揭示土壤铬与光谱变量间关系的空间分异规律的同时,又能尽可能包含多的信息量,是GWR模型最优光谱分辨率选择的关键。前人研究中光谱采样间隔从1—256 nm不等,但是不同研究区域选择的采样间隔具有较大的差异[20],甚至出现了光谱分辨率越高对土壤铬的定量反演能力越好[11]以及光谱分辨率越低模型精度越高[11]两种截然相反的矛盾观点。本研究中,GWR模型以10 nm分辨率效果最优,不仅预测能力最强,且较OLS模型的改善效果显著,为土壤铬GWR预测的最佳光谱分辨率,故本文在10 nm分辨率尺度下,利用反射率的二阶微分和反射率倒数的二阶微分进行土壤铬元素的GWR模型构建。

3.4 土壤铬高光谱预测的GWR模型

为尽量保证建模样本与验证样本范围一致,将131个样本数据按全铬含量从大到小排列,每隔两个样品取一个作为验证样本,共43个(33%),其余的88个(67%)作为建模样本。其中,88个建模样本的土壤铬含量分布范围为(26.35±18.67) mg/kg,变异系数为70.85%,用于模型验证的的43个样本铬含量分布范围为(25.68±16.24)mg/kg,变异系数为63.24%,与建模样本的变化幅度较为一致。

在10 nm光谱分辨率尺度下,以1440 nm的反射率的二阶微分(SD_1440)和430 nm的反射率倒数的二阶微分(RTSD_430)为自变量,土壤全铬含量为因变量,分别构建OLS和GWR的土壤全铬含量估算模型。模型的预测效果由较小的AIC值和残差平方和,较大的R2和调节R2进行判断(表5)。

表5 土壤重金属的OLS及GWR回归的模型参数比较

从表5可知,GWR模型的AIC值明显小于OLS模型,说明利用GWR模型进行土壤铬预测的效果要明显好于OLS模型。决定系数R2、调整R2和残差平方和进一步证实这一情况。GWR模型中,光谱变量对土壤铬的回归解释度达71.6%,较OLS模型(解释度为26.6%),提高了45%。且GWR模型回归的残差平方和为5441.275,远小于OLS模型的21484.197,进一步说明GWR法进行土壤铬预测的模型效果较OLS法有了显著的提升。

为了更好地说明所构建模型的有效性,用43个未参与建模的采样点数据分别带入构建的OLS和GWR模型进行土壤铬预测。预测效果选用最大(正负)估计误差(±MEE)、平均误差(ME)、均方根误差(RMSE)、OLS和GWR模型预测值与实测值的相关系数(R)、回归的决定系数(R2)来进行评价,相关参数如表6所示。

表6 OLS和GWR模型预测效果的相关指标

如果预测误差是无偏的,即预测值与实测值接近,平均误差接近于0,均方根误差值越小,模型预测精度越高。从表5可以看出,OLS模型和GWR模型平均误差绝对值较为接近,均较接近于0,但GWR模型的最大正负误差及均方根误差小于OLS模型,说明GWR模型的预测精度高于OLS模型。验证样本的GWR模型预测值与实测值之间的相关系数及R2均远大于OLS模型,进一步证实GWR模型的预测精度明显高于OLS模型。这主要是因为土壤铬的空间分布同时受各种自然因素和人为活动影响,具有复杂的空间变异性和非平稳性,土壤光谱特征则是土壤有关性质的综合反映,故在不同的研究区域,不同的位置,由于土壤类型、组分和污染水平不同,土壤铬含量与光谱特征的关系也可能是不同的。如果使用传统的全局预测模型进行重金属含量的高光谱估算,得到的回归参数将是整个区域内回归参数的平均值,回归结果不能真实地反映二者关系的空间特征。为了探测参数的空间变化,GWR模型对OLS模型进行了扩展,模型假设距离越近的样点其影响越显著,其使用核函数来确定空间依赖性(空间自相关性)的空间范围,并利用距离衰减函数来对此空间范围内样点进行加权计算[44]。模型允许参数在空间区域上有一定的变化,通过各空间位置上的参数预测值随空间位置的变化情况,可以非常直观地探测空间关系的非平稳性,可以有效地提高土壤铬的高光谱预测精度。目前GWR模型已经发展成一门较为成熟的空间统计学技术,这种估算方法不但简单易行,估算结果有明确的解析表示,得到的参数估计还能进行统计检验,同时也有GWR3.0和ArcGIS 10.2等相对成熟的软件,该方法可为土壤铬的高光谱预测提供新的思路。

3.5 土壤铬GWR预测的稳定性分析

为了更好地说明模型预测的效果及其稳定性,将样本数据按全铬含量从大到小排列,设计不同的建模和验证数据样本比例,分别构建土壤铬预测的GWR模型和OLS模型(表7),各模型均通过P<0.05的F检验。发现建模样本与验证样本除了比例为1∶1(66个建模样本)时, GWR模型与OLS模型的拟合效果相差不大,其他比例进行土壤铬含量预测时,GWR模型回归的效果均明显优于OLS模型。随着建模样本比例的增大,GWR模型的回归效果呈现提高-下降-提高的变化趋势,其中以建模样本与验证样本比例为1∶1时,效果最差,比例为2∶1(88个建模样本)时,GWR模型的回归效果最佳。比例从4∶1(105个建模样本)开始,随着建模样本比例的增大,GWR模型的回归效果呈较为稳定的增长趋势,这说明了GWR模型在土壤铬含量预测中的表现总体上来说较为稳定,但建模样本数较少时,拟合效果可能出现波动现象,随着建模样本的增加,其表现逐渐趋于稳定,GWR模型适合大样本土壤铬的空间拟合。

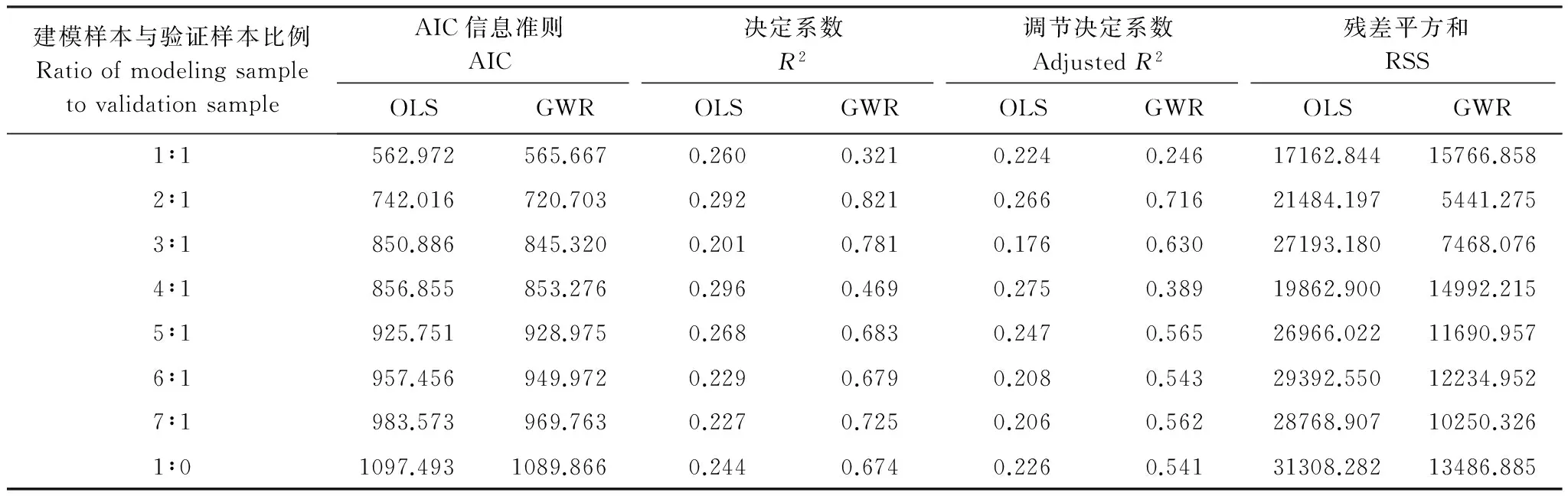
表7 采样点密度对模型预测效果的影响

4 结论

(1)本研究表明10 nm光谱分辨率尺度下,以1440 nm的反射率的二阶微分(SD_1440)和430 nm的反射率倒数的二阶微分(RTSD_430)为自变量,土壤全铬含量为因变量,构建的GWR模型对土壤铬含量预测效果最好,表现为模型具有最大的R2和调节R2值,最小的残差平方和,精度较OLS模型有显著提高。

(2)土壤铬预测模型的精度受光谱分辨率影响。对于OLS预测模型来说,3 nm分辨率的模型预测效果最好,而对于GWR预测模型来说,10 nm分辨率的模型不仅预测效果最好,其相较于OLS模型的改善作用显著,为土壤铬含量GWR预测的最佳光谱分辨率。该光谱分辨率即为EO- 1Hyperion高光谱影像的光谱分辨率。

(3)光谱变换对模型的预测效果具有明显的提高作用。虽然光谱变换(除光谱一阶微分外)值与土壤铬的最大相关系数均小于原始反射率与铬的最大相关系数,对土壤铬的光谱特征未起到增强作用,但在不同光谱分辨率尺度下,这些变换光谱在重金属铬的预测模型构建中均有较好的表现,很好地提高土壤重金属铬的预测效果。

(4)GWR模型的回归效果受建模样本与验证样本比例的影响。GWR模型在建模样本数较少时,其预测效果出现波动现象,随着建模样本的增加,其表现逐渐趋于稳定,说明GWR模型适合大样本土壤铬的空间拟合。结合Hyperion高光谱影像,解决实验室光谱向卫星影像光谱的尺度转换问题,GWR模型容易实现从实验室尺度向区域尺度的推广,为实现大范围格网尺度的土壤铬空间预测提供可能。

[1] Wang Q Y D, Cui Y, Liu X. Instances of soil and crop heavy metal contamination in China. Soil and Sediment Contamination: An International Journal, 2001, 10(5): 497- 510.

[2] Wei B G, Yang L S. A review of heavy metal contaminations in urban soils, urban road dusts and agricultural soils from China. Microchemical Journal, 2010, 94(2): 99- 107.

[3] Li Z Y, Ma Z W, Van Der Kuijp T J, Yuan Z W, Huang L. A review of soil heavy metal pollution from mines in China: Pollution and health risk assessment. Science of the Total Environment, 2014, 468- 469: 843- 853.

[4] Zhang X Y, Zhong T Y, Liu L, Zhang X M, Cheng M, Li X H, Jin J X. Chromium occurrences in arable soil and its influence on food production in China. Environmental Earth Sciences, 2016, 75(3): 257- 257.

[5] Paul D, Choudhary B, Gupta T, Jose M T. Spatial distribution and the extent of heavy metal and hexavalent chromium pollution in agricultural soils from Jajmau, India. Environmental Earth Sciences, 2015, 73(7): 3565- 3577.

[6] Liu H B, Guo P T, Wu W, Wang Z Y. Assessment of soil arsenic, chromium, mercury, and lead at an agricultural landscape scale. Soil and Sediment Contamination: An International Journal, 2011, 20(8): 995- 1007.

[7] Landrot G, Tappero R, Webb S M, Sparks D L. Arsenic and chromium speciation in an urban contaminated soil. Chemosphere, 2012, 88(10): 1196- 1201.

[8] Gitet H, Subramanian P A, Minilu D, Kiros T, Hilawie M, Gebremariam G, Taye K. Speciation of chromium in soils near Sheba Leather Industry, Wukro Ethiopia. Talanta, 2013, 116: 626- 629.

[9] 多克辛. 土壤优控污染物监测方法. 北京: 中国环境科学出版社, 2012: 162- 169.

[10] Araújo S R, Demattê J A M, Vicente S. Soil contaminated with chromium by tannery sludge and identified by vis-NIR-mid spectroscopy techniques. International Journal of Remote Sensing, 2014, 35(10): 3579- 3593.

[11] Wu Y Z, Chen J, Wu X M, Tian Q J, Ji J F, Qin Z H. Possibilities of reflectance spectroscopy for the assessment of contaminant elements in suburban soils. Applied Geochemistry, 2005, 20(6): 1051- 1059.

[12] Wu Y Z, Chen J, Ji J F, Gong P, Liao Q L, Tian Q J, Ma H R. A mechanism study of reflectance spectroscopy for investigating heavy metals in soils. Soil Science Society of America Journal, 2007, 71(3): 918- 926.

[13] Song Y X, Li F L, Yang Z F, Ayoko G A, Frost R L, Ji J F. Diffuse reflectance spectroscopy for monitoring potentially toxic elements in the agricultural soils of Changjiang River Delta, China. Applied Clay Science, 2012, 64: 75- 83.

[14] 李淑敏, 李红, 孙丹峰, 周连第, 鲍京. 基于热红外特征光谱的土壤重金属含量估算模型研究. 红外, 2010, 31(7): 33- 38.

[15] 吴明珠, 李小梅, 沙晋明. 亚热带土壤铬元素的高光谱响应和反演模型. 光谱学与光谱分析, 2014, 34(6): 1660- 1666.

[16] 徐明星, 吴绍华, 周生路, 廖富强, 马春梅, 朱诚. 重金属含量的高光谱建模反演: 考古土壤中的应用. 红外与毫米波学报, 2011, 30(2): 109- 114.

[17] Lian S, Ji J, Tan D J, Xie H B, Luo Z F, Gao B. Estimate of heavy metals in soil and streams using combined geochemistry and field spectroscopy in Wan-sheng mining area, Chongqing, China. International Journal of Applied Earth Observation and Geoinformation, 2015, 34: 1- 9.

[18] 王菲, 曹文涛, 康日斐, 曹见飞, 吴泉源. 基于野外实测光谱的金矿区土壤重金属铬监测研究. 环境污染与防治, 2016, 38(2): 13- 18.

[19] 龚绍琦, 王鑫, 沈润平, 刘振波, 李云梅. 滨海盐土重金属含量高光谱遥感研究. 遥感技术与应用, 2010, 25(2): 169- 177.

[20] 刘华, 张利权. 崇明东滩盐沼土壤重金属含量的高光谱估算模型. 生态学报, 2007, 27(8): 3427- 3434.

[21] Song Y X, Ji J F, Mao C P, Ayoko G A, Frost R L, Yang Z F, Yuan X Y. The use of reflectance visible-NIR spectroscopy to predict seasonal change of trace metals in suspended solids of Changjiang River. CATENA, 2013, 109: 217- 224.

[22] 袁中强, 曹春香, 鲍达明, 陈伟, 田蓉, 俄尕, 李华. 若尔盖湿地土壤重金属元素含量的遥感反演. 湿地科学, 2016, 14(1): 113- 116.

[23] Dong Y W, Yang S Q, Xu C Y, Li Y Z, Bai W, Fan Z N, Wang Y N, Li Q Z. Determination of soil parameters in apple-growing regions by near-and mid-infrared spectroscopy. Pedosphere, 2011, 21(5): 591- 602.

[24] Shi T Z, Chen Y Y, Liu Y L, Wu G F. Visible and near-infrared reflectance spectroscopy-An alternative for monitoring soil contamination by heavy metals. Journal of Hazardous Materials, 2014, 265: 166- 176.

[25] Huo X N, Zhang W W, Sun D F, Li H, Zhou L D, Li B G. Spatial pattern analysis of heavy metals in Beijing agricultural soils based on spatial autocorrelation statistics. International Journal of Environmental Research and Public Health, 2011, 8(12): 2074- 2089.

[26] Krami L K, Amiri F, Sefiyanian A, Shariff A R B M, Tabatabaie T, Pradhan B. Spatial patterns of heavy metals in soil under different geological structures and land uses for assessing metal enrichments. Environmental Monitoring and Assessment, 2013, 185(12): 9871- 9888.

[27] Zhong B Q, Liang T, Wang L Q, Li K X. Applications of stochastic models and geostatistical analyses to study sources and spatial patterns of soil heavy metals in a metalliferous industrial district of China. Science of the Total Environment, 2014, 490: 422- 434.

[28] Nanos N, Martín J A R. Multiscale analysis of heavy metal contents in soils: Spatial variability in the Duero river basin (Spain). Geoderma, 2012, 189- 190: 554- 562.

[31] 李清良, 吴倩, 高进波, 马军, 徐秋芳, 俞慎. 基于小流域尺度的土壤重金属分布与土地利用相关性研究——以厦门市坂头水库流域为例. 生态学报, 2015, 35(16): 5486- 5494.

[32] 吴文勇, 尹世洋, 刘洪禄, 潘兴瑶, 宝哲. 污灌区土壤重金属空间结构与分布特征. 农业工程学报, 2013, 29(4): 165- 173.

[33] 仝致琦, 陈太政, 段海静, 谷蕾, 马建华. 不同耕作方式对路旁土壤重金属分布的影响——以黄淮平原国道310开封段为例. 地理科学, 2014, 34(3): 377- 384.

[34] Fortheringham A, Chanrlton M, Brunsdon C. The geography of parameter space: An investigation of spatial non-stationarity. International Journal of Geographical Information Systems, 1996, 10(5): 605- 627.

[35] Jaber S M, Al-Qinna M I. Global and local modeling of soil organic carbon using Thematic Mapper data in a semi-arid environment. Arabian Journal of Geosciences, 2015, 8(5): 3159- 3169.

[36] Propastin P. Modifying geographically weighted regression for estimating aboveground biomass in tropical rainforests by multispectral remote sensing data. International Journal of Applied Earth Observation and Geoinformation, 2012, 18: 82- 90.

[37] Wang K, Zhang C R, Li W D. Predictive mapping of soil total nitrogen at a regional scale: A comparison between geographically weighted regression and cokriging. Applied Geography, 2013, 42: 73- 85.

[38] Wang K, Zhang C R, Li W D, Lin J, Zhang D X. Mapping soil organic matter with limited sample data using geographically weighted regression. Journal of Spatial Science, 2014, 59(1): 91- 106.

[39] 国家环境保护局. GB/ T15618- 1995 土壤环境质量标准. 北京: 中国标准出版社, 2006.

[40] 陈振金, 陈春秀, 刘用清, 吴瑜端, 杨孙楷, 卢昌义. 福建省土壤环境背景值研究. 环境科学, 1992, 13(4): 70- 75.

[41] 解宪丽, 孙波, 郝红涛. 土壤可见光——近红外反射光谱与重金属含量之间的相关性. 土壤学报, 2007, 44(6): 982- 993.

[42] Qiu Y, Fu B, Wang J, Chen L, Meng Q, Zhang Y. Spatial prediction of soil moisture content using multiple-linear regressions in a gully catchment of the Loess Plateau, China. Journal of Arid Environments, 2010, 74(2): 208- 220.

[43] 王库. 基于地理权重回归模型的土壤有机质空间预测. 土壤通报, 2013, 44(1): 21- 28.

[44] Fotheringham A S, Brunsdon C, Charlton M N. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships. New York: Wiley, 2002.

StudyonGWRmodelappliedforhyperspectralpredictionofsoilchromiuminFuzhouCity

JIANG Zhenlan1,2, YANG Yusheng1, SHA Jinming1,*

1CenterforPost-doctoralStudiesofGeographicalScience,SchoolofGeographicalScience,FujianNormalUniversity,Fuzhou350007,China2GeographicalSciencesDepartment,MinjiangUniversity,Fuzhou350108,China

Inversion models applied for hyperspectral prediction of soil chromium include univariate regression, multiple linear regression, principal component regression, and partial least squares regression models. They are mostly based on the presumed homogeneous influence of heavy metal content on spectral reflectance at different locations. This presumption, however, ignores the spatial heterogeneity of correlation between soil chromium and spectral variables. In contrast, Geographically Weighted Regression(GWR) model effectively reveals the spatial heterogeneity among different variables, as is evidenced in many studies involving the spatial prediction of soil properties. In this study, we first analyzed the influence of different spectral resolutions and transformations on soil chromium-targeted hyperspectral prediction model. Thereafter, optimal spectral resolution and variables were selected to establish the GWR model for prediction of soil chromium content in Fuzhou City. In addition, the applicability and limitations of the model were assessed by comparing the predictions based on GWR and Ordinary Least Squares Regression(OLS)models separately. The conclusions finally drawn from the study are as follows: (1) At a resolution of 10 nm, with soil chromium content as a dependent variable and the second derivative of reflectance and reflectance reciprocal as independent variables, the GWR model displayed the best prediction performance. The values ofR2and the adjustedR2were 0.821 and 0.716, respectively, which showed an increase of 0.529 and 0.450, respectively, above the corresponding values in the OLS model. The AIC was decreased by 22 units to 720.703, and the residual sum of squares was decreased by three quarters, an indication of significant improvement of the prediction performance. (2) The spectral resolution exerted obvious influence on the accuracy of chromium prediction models. The GWR model, with a spectral resolution of 10 nm, as against the OLS model, with a resolution of 3 nm, showed optimal prediction outcome and an evident increase in accuracy. The best resolution for the GWR model was 10 nm. (3) The spectral transformation of first-order differential effectively enhanced the spectral features of soil chromium. Whereas other spectral transformations failed to enhance the features, they significantly improved the prediction performance. (4) The optimal spectral resolution of 10 nm for GWR-based soil chromium prediction was up to the level of EO- 1 Hyperion images. Moreover, the prediction performance of the GWR model showed a tendency to stabilize with the increase in the number of sample sites, which is suitable for soil chromium prediction in the regions featuring great spatial heterogeneity. Therefore, with hyper-spectral images, the application of GWR model can be extended from laboratory to the regional scale, making the spatial prediction of soil chromium on grid basis feasible.

soil heavy metal chromium; GWR model; hyper-spectral; spectral resolution; spectral transformation

国家自然科学青年基金项目(41601601)；福建省自然科学基金项目(2016J01194);科技部国际合作重大专项(247608)； 欧亚土地保护研究国际大学合作项目(561841-EPP-1-2015-1-IT-EPPKA2-CBHE-JP)

2016- 09- 28; < class="emphasis_bold">网络出版日期

日期:2017- 08- 14

*通讯作者Corresponding author.E-mail: jmsha@fjnu.edu.cn

10.5846/stxb201609281969

江振蓝,杨玉盛,沙晋明.福州市土壤铬含量高光谱预测的GWR模型研究.生态学报,2017,37(23):8117- 8127.

Jiang Z L, Yang Y S, Sha J M.Study on GWR model applied for hyperspectral prediction of soil chromium in Fuzhou City.Acta Ecologica Sinica,2017,37(23):8117- 8127.