尾矿库排洪系统竖井深度对泄流能力的影响研究

王耀宇，佘成学，陈昱钦，陈俊宇，贾 攀，尹志强，李 杨，金俊超

(武汉大学 水资源与水电工程科学国家重点实验室， 湖北 武汉 430072)

尾矿库排洪系统竖井深度对泄流能力的影响研究

王耀宇，佘成学，陈昱钦，陈俊宇，贾 攀，尹志强，李 杨，金俊超

(武汉大学 水资源与水电工程科学国家重点实验室， 湖北 武汉 430072)

通过水露沟尾矿坝加高扩容工程，研究尾矿库排洪系统竖井深度对泄流能力的影响规律。在该工程中，有9个排洪支系统的排水井内外径、竖井内径、隧洞断面一致，而竖井深度不一致。选取其中3个代表性的排洪支系统，改变排水井的进水口高程，进行水工模型试验，得到了一系列的排水井进水水头与泄流量的关系曲线。以此为基础，通过实验数据分析不同竖井深度对泄流量的影响规律，建立泄流量与竖井深度之间的拟合函数关系。

尾矿库；竖井深度；泄流能力；水工模型试验

水露沟尾矿库[1]一期设计总坝高135 m，总库容1 473×104m3。该尾矿库设计采用初期坝+后期上游法堆坝形式，其中初期尾矿坝坝高60 m，坝底标高1 090 m，坝顶标高1 150 m；初期坝顶以上设计平均堆积边坡1∶5.0，一期上游法尾砂堆积至1 225 m标高。水露沟尾矿库加高扩容工程，是在现有一期工程的基础上，继续采用上游法加高，堆积至1 388 m标高，如此形成的尾矿库总坝高298 m，总库容约1.5 亿m3，有效库容13 506.48 万m3。

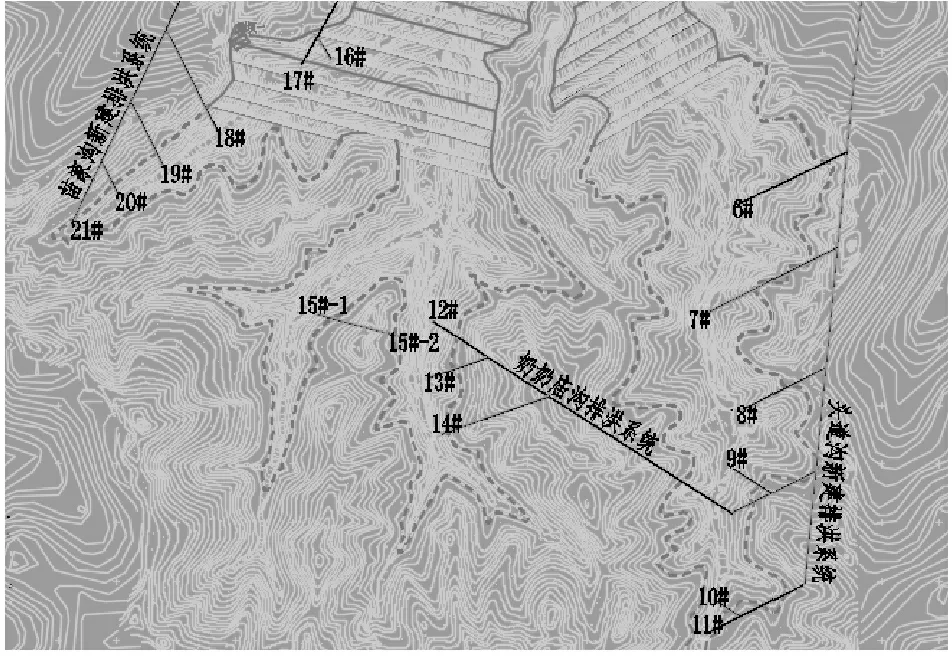
图1水露沟尾矿库新增排洪系统布置图

水露沟尾矿库加高扩容后，新增的排水井[2]为6#—21#共16个，见图1。其中6#—11#属头道沟排洪系统，12#—14#属奶奶庙沟排洪系统，16#—21#属苗家沟排洪系统。其中奶奶庙沟的新建排洪系统，通过排水隧洞，与头道沟新建的排洪系统相连通。

目前，国内针对排洪系统进行了很多的水工模型试验，但一般所含的排水井数量相对较少，常用包括排水井、竖井、消能井、支隧洞及主隧洞的整体模型进行试验研究[3-4]。

由于水露沟尾矿库新增排水井数量较多，用传统的整体模型进行试验研究，将消耗很大的人力、物力。如果我们将排水井、竖井、消能井[5-6]、支隧洞称为排洪支系统，则水露沟的排洪系统共新增16个排洪支系统。其中，有9个排洪支系统的排水井、竖井、消能井、支隧洞、主隧洞的断面尺寸相同，而竖井深度相差很大，从6.0 m变化到104.2 m不等。对于这9个排洪支系统，如果选取若干代表性的排洪支系统，用排水井、竖井、消能井、支隧洞和部分主隧洞构成局部模型进行试验，研究其排水能力随竖井深度的变化规律，进一步推广应用于其他深度的排洪支系统的排水能力评估，则一方面可大大减少试验工作量；另一方面有助于加深对排水能力随竖井深度的变化规律的认识，也有助于指导同类排洪系统的设计。

本文选取9#、11#和13#3三个排洪支系统作为代表，通过水工模型试验，得到一系列排水井进水水头与泄流量的关系曲线，以此为基础，分析不同竖井深度对泄流量的影响规律，并建立泄流量与竖井深度之间的拟合函数关系，用于其他排洪支系统排洪能力的评估[7]。

1 模型设计

9#、11#、13#排洪支系统的排水井内径为4.0 m，外径为4.5 m，每层开有8个窗口，窗口高度为2.65 m，宽度为1.17 m；框架立柱宽度为0.40 m，横梁厚度为0.35 m。竖井内径为3.0 m。支隧洞断面为城门洞型，高3.0 m，宽2.5 m。排洪支系统原型结构尺寸见表1，排洪支系统结构参见图2，其中主隧洞未画出。

表1 排洪支系统结构原型尺寸

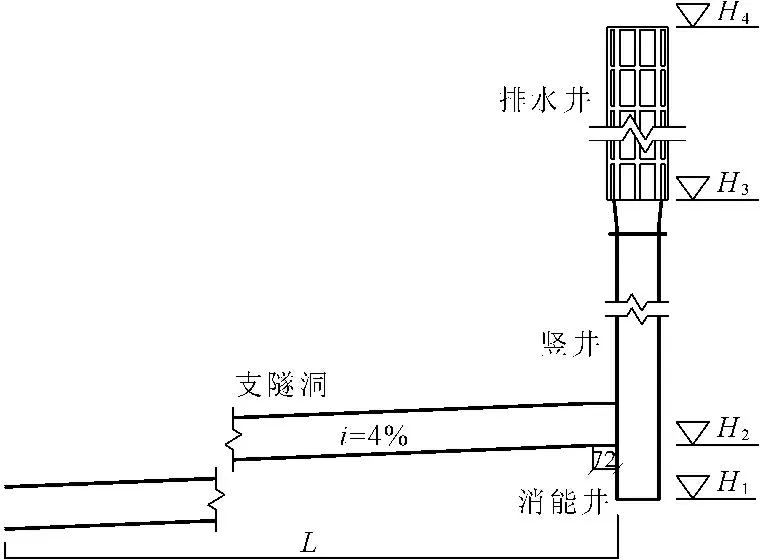
图2排洪支系统结构图

由于重力起着主导作用，依据满足主导力相似的原则，在水流相似方面按重力相似准则(弗劳德准则)设计模型[8]，并满足紊动阻力相似要求[9]，选取模型的几何比尺为1∶25，相应的各物理量比尺见表2。

对于主隧洞，断面较支隧洞大，底坡也较大，在一般情况下，水流为明渠急流，流态单一。如果不需要了解主隧洞中流态变化情况，则不需要把整个主隧洞全部纳入，按整体模型进行研究。由此，对于9#、11#和13#排洪支系统，可取其排水井、竖井、消能井、支隧洞以及部分主隧洞制作局部模型进行试验，以了解排洪支系统的排水能力和水流流态变化情况。其中主隧洞只对排洪支系统起到水流边界的作用，因此，不需要特别长。

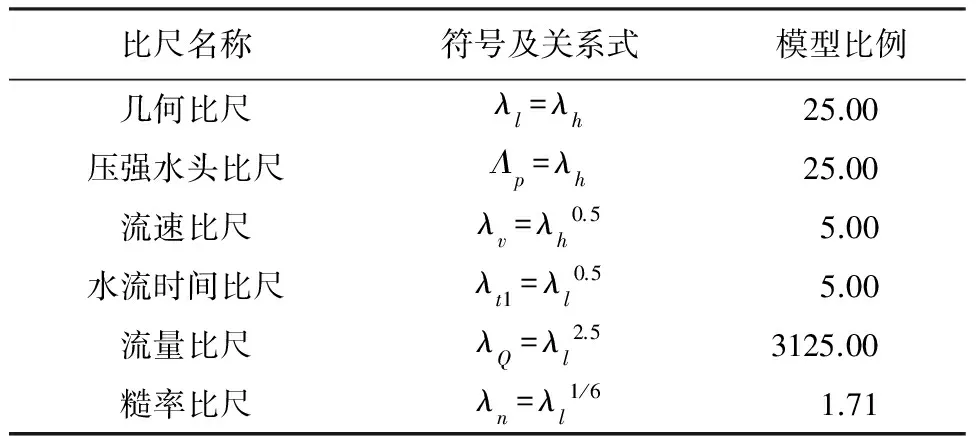
表2 模型比尺表

有机玻璃糙率与按表2中糙率比尺折算后的混凝土糙率一致，因此选用有机玻璃制作排洪支系统模型。制作的模型见图3和图4。其中，9#和11#排洪支系统共用一个水箱模拟水库，尺寸为1.5 m×1.7 m×1.7 m；13#排洪支系统与尺寸为1.8 m×2.0 m×1.7 m水箱相连，模拟水库。当一个支系统试验时，共用水箱的另一个排洪支系统封堵住，因此，在试验时，共用水箱的两个排洪支系统相互没有影响。

图3 9#、11#排洪支系统外观情

9#、11#、13#排水井总高度分别为30 m、20 m和30 m。随大坝加高，排水井逐步封堵，即进水口位置不断抬高。对于试验而言，不可能完全按实际封堵[10]过程进行试验，而是选择若干进水口高程进行试验。根据排水井的高度，以及为了不同排水井排水情况的横向比较，分别在底部、中部和顶部位置，选择2～3个进水口位置，具体见表3。

图4 13#排洪支系统外观情况

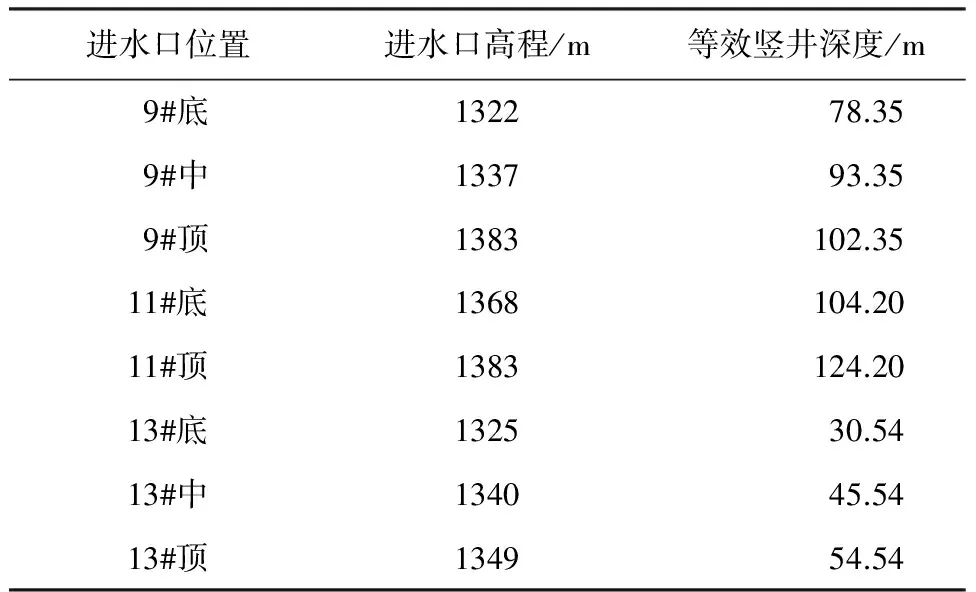
表3 排水井进水口位置及等效竖井深度

以9#排洪支系统为例，三个不同进水口位置的具体情况见图5。

图5 9#排水井不同位置进水口情况

从图5中也可以看到，排水井封堵部分相当于增加了竖井的深度。如果将竖井深度加上封堵的排水井高度相加看做是等效的竖井深度，则对于不同的进水口位置，就有不同的等效竖井深度。对于表3中的9#、11#、13#排水井，根据进水口位置的不同，共有8种等效排水井深度。

根据干滩长度的需要，对于每一个进水口位置，水头不能超过6 m，即对于试验而言，试验水头控制在6 m范围以内。

排水井进水水头通过测针测量水位后推算得到，流量用电磁流量计测量。

2 试验过程和成果分析

2.1 试验过程

确定某一级流量，用阀门调节控制进水流量，待水位稳定后，测水箱中的水位，便可得一个流量-水位数据对；同时观测排水井、竖井、消能井和泄洪支洞中的流态情况。

确定下一级流量，用同样的方式，重复上述试验，测得下一个流量-水位数据对；以及得到各部位相应的流态。

对于某一高程的进水口位置，需要测若干个流量-水位数据对，用于绘制水头-流量关系曲线。在本项目中，我们一般侧11～14个数据对。

2.2 试验成果分析

对于表3所示的9#、11#、13#排洪系统的8种进水口高程情况，分别进行试验，共测得8条流量-进水口水头关系曲线，见图6。

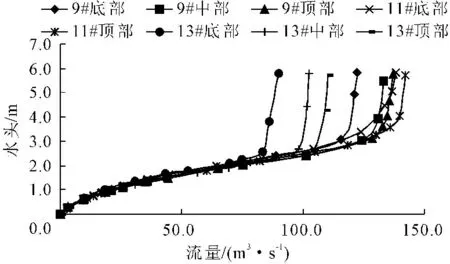
图6各排洪支系统流量-水头关系曲线

从图6可以看出：

(1) 对于不同的竖井深度，流量-进水口水头关系曲线变化规律大致类似，均可分为平稳上升段、拐弯段、快速上升段三段，以9#底部进水口泄流能力曲线为例，见图7。

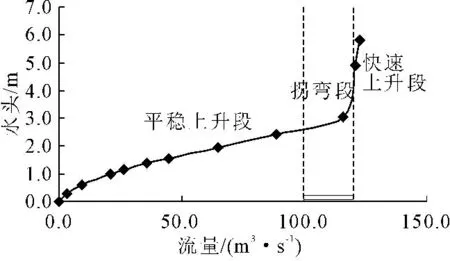
图7 9#底部进水口流量-水头关系曲线分段情况

在曲线平稳上升段，泄洪支洞中的水流基本为明渠流。即使随流量增大，竖井中的水深增加，淹没了支隧洞进水口位置，但绝大部分支隧洞中水流仍然为明渠流，排水井自由排水，所以整个支系统中的排水完全由排水井控制。

随着流量和水头增加，竖井中水位向上升高，排水井进入到淹没出流的状态，此时，支隧洞中的水流还不是完全有压，整个支系统的泄水能力由排水井、竖井和支隧洞共同控制，这一过程一直延续到支隧洞完全为有压流为止。整个过程的流量-水头关系曲线就是图中的拐弯段。对于拐弯段，要确切获得其变化范围，需要在其变化范围内大量增加流量-进水口水头数据对，一般情况下很难精确得到其变化范围。

随着流量和水头进一步增加，支隧洞中完全为有压流，竖井中也是满管流，排水井内外基本没有水头差，整个系统完全处于一种有压流状态，在本项目中，支隧洞的泄流能力相对较小，起控制作用。此时的流量-水头关系曲线为快速上升段，流量少量增加，水头增加很大。

(2) 对于不同的竖井深度，竖井浅的平稳上升段曲线与竖井深的平稳上升段曲线相重合，但竖井深的平稳上升段曲线的水头和流量变化范围更大，即竖井深的平稳上升段曲线包含了竖井浅的平稳上升段曲线。曲线重合的原因是：各排洪支系统的排水井进水部分尺寸完全相同，而此时泄水能力由排水井控制，反映在曲线中，就是部分曲线重合。

(3) 对于不同的竖井深度，其曲线拐弯段差异很大，竖井深的排洪支系统的拐弯段处于更大的水头和流量位置。导致这一现象的原因是：竖井深度越深，总水头越大，在竖井、支隧洞中的流速增大，从而增加了整个排洪支系统的排水能力，反映在曲线中，各排洪支系统的拐弯段位置不在同一位置，且差异很大。

对于拐弯段的流量，尽管无法确切确定其拐弯段的确切范围，但根据试验得到的流量-水头数据对，通过拟合，可得到拐弯段的大致范围。我们在拐弯段范围内，找一个点，使得该点的转弯段曲线的切线斜率为1，将此点作为拐弯点。在所有的拐弯段内都能找到这样一个拐弯点，将该点的流量和等效竖井深度建立拟合函数关系，具体为：

Y=-0.0029X2+0.9719X+58.568

(1)

其中：Y表示拐弯点流量；X表示等效竖井深度；拟合相关系数为0.9873。将此函数绘图，具体见图8。由图8可以看到，拐弯点流量与等效竖井深度之间大致符合抛物线函数关系。

同样，可以得到拐弯点水头和竖井深度之间的拟合函数关系，具体为：

Y=6×10-5X2+0.0012X+2.4852

(2)

其中：Y为拐弯点水位；X为等效竖井深度；拟合相关系数为0.9097。将此函数绘图，具体见图9。由图9可以看到，拐点水位与等效竖井深度之间大致符合抛物线函数关系。

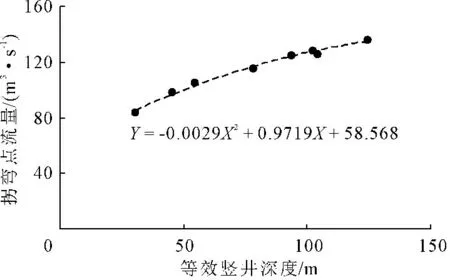
图8 拐弯点流量-等效竖井深度关系曲线

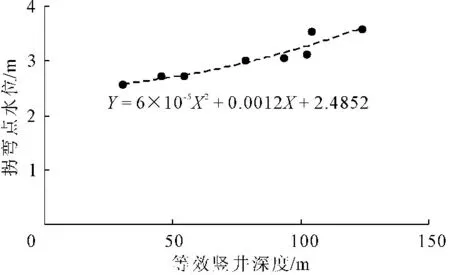
图9拐弯点水位-等效竖井深度关系曲线

(4) 对于不同的竖井深度，其快速上升段位置差异也很大，竖井深度越深，其泄流能力越大，在相同水头条件下，具有更大的下泄流量。

如果统一取水头为5.9 m时的泄流量，与等效竖井深度建立拟合函数关系，则可以得到：

Y=-0.003X2+1.0458X+61.206

(3)

其中：Y表示最大流量；X表示竖井等效深度；拟合相关系数为0.997。将此函数绘图，具体见图10。由图10可以看到，最大流量与等效竖井深度之间大致符合抛物线函数关系。

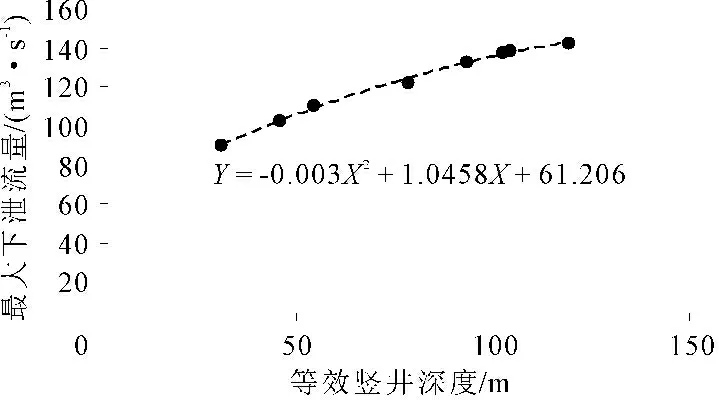
图10最大流量-等效竖井深度曲线

通过上述分析，我们深入了解了不同竖井深度的泄流能力变化规律，进一步可以以此推测其他竖井深度的排洪支系统的泄流能力。具体而言，对于某一个竖井深度的排洪支系统，利用图6提供的曲线，得到排水井起控制作用时的流量-水头关系曲线；通过式(1)、式(2)推测拐弯点的流量和水头；利用式(3)推测5.9 m水头时的流量，由此建立水头-流量关系曲线，尽管在拐弯段和快速上升段与真实情况有些差异，但是偏安全的，可以满足水露沟其他排洪系统的排洪能力的估算。同时该尾矿库运行的任一时期，有且仅有一个排水井发挥作用，当新的排水井发挥作用时，旧的排水井则被封堵。固排洪系统总流量等于正在发挥作用的排水井的流量，因此不对系统的总过流能力[11-12]做相应研究。限于篇幅，利用水头-流量曲线的调洪过程以及泄流安全性判断等方面内容，不再赘述。

3 结 论

通过上述试验研究，得出以下结论：

(1) 对于不同的竖井深度，流量-进水口水头关系曲线变化规律大致类似，均可分为平稳上升段、拐弯段、快速上升段三段，分别对应于排水井起控制作用，排水井、竖井和支隧洞共同起控制作用和排水支洞起控制作用阶段。

(2) 对于不同的竖井深度，竖井浅的平稳上升段曲线与竖井深的平稳上升段曲线相重合，但竖井深的平稳上升段曲线的水头和流量变化范围更大，即竖井深的平稳上升段曲线包含了竖井浅的平稳上升段曲线。

(3) 对于不同的竖井深度，其曲线拐弯段差异很大，竖井深的排洪支系统的拐弯段处于更大的水头和流量位置。

(4) 对于不同的竖井深度，其快速上升段位置差异也很大，竖井深度越深，其泄流能力越大，在相同水头条件下，具有更大的下泄流量。

(5) 根据上述研究结果，可以推断其他竖井深度情况下排洪支系统的水头-流量关系曲线，并用于排洪安全性分析。

[1] 邓书申.尾矿库排洪系统设计及优化方法[J].金属矿山，2014,43(2):146-149.

[2] 陈 欢,唐文超,张强强.某新型窗口式排水井的设计及应用[J].有色冶金设计与研究,2014,35(5):92-93.

[3] 张 进,乐 陶,曹纪刚.头石山尾矿库排洪构筑物水工模型试验研究[J].金属矿山,2013,42(1):30-32.

[4] 曹本清.桃源水库枢纽工程竖井式溢洪道布置探讨[J].大科技,2015(11):101-102.

[5] 陈小威,张宗孝,刘 冲,等.基于消能井井深变化下的竖井溢洪道压强试验研究[J].应用力学学报,2016,35(5):826-831.

[6] 邓建伟,花立峰,安梦雄.龙抬头式泄洪洞体型设计与泄洪消能问题研究[J].水利与建筑工程学报,2013,11(3):165-168.

[7] 周志广,李 平,郭 锐.桓仁某尾矿库排洪系统防洪能力可靠性分析[J].矿业工程,2016,14(6):52-55.

[8] 赵 昕，张晓元.水力学[M].北京：中国电力出版社，2009.

[9] 中华人民共和国水利部.水工(常规)模型试验规程：SL 155—2012[S]．北京：中国水利水电出版社，2012.

[10] 乔云航,崔晓明,肖圣博.谈某尾矿库排水系统封堵技术措施[J].山西建筑,2013,39(5):107-109.

[11] 刘小良,张朋鹤,王 鑫.龙潭水库导流泄洪洞运行水力特性研究[J].水利与建筑工程学报,2015,13(4):159-161.

[12] 陈 欢,李瑞林,贾 晔,等.排水系统泄流能力计算方法探讨[J].现代矿业,2015(2):180-183.

InfluenceofShaftDepthonDischargeCapacityofTailingsPondFloodSystem

WANG Yaoyu, SHE Chengxue, CHEN Yuqin, CHEN Junyu, JIA Pan,YIN Zhiqiang, LI Yang, JIN Junchao

(StateKeyLaborataroyofWaterResourcesandHydropowerEngineeringSciences,WuhanUniversity,Wuhan,Hubei430072,China)

In this paper the influence of shaft depth on discharge capacity of tailings pond flood system was analyzed based on the Shuilugou tailings dam heightening engineering. There are 9 flood systems whose inner diameter and outer diameter of the drainage well, inner diameter of the shaft and the tunnel sections are consistent, while they have different shaft depth. By selecting 3 representative flood systems and changing the intake elevation of the drainage well, we carried out the hydraulic model experiment, from which a series of relation curves between water head and flow rate of the drainage well were obtained. Basing on the curves, the experiment data can then be used to analyze the influence rule of different shaft depth on the flow rate, and establish the fitting function.

tailingspond;shaftdepth;dischargecapacity;hydraulicmodelexperiment

10.3969/j.issn.1672-1144.2017.06.026

2017-06-21

2017-07-24

王耀宇(1994—)，男，湖北咸宁人，硕士研究生，研究方向为边坡稳定。 E-mail: 463415663@qq.com

TV131.61

A

1672—1144(2017)06—0133—05