一种优化的严反馈非线性系统反推控制

潘建雄，孙 卡

（南昌航空大学 信息工程学院，南昌 330063）

一种优化的严反馈非线性系统反推控制

潘建雄，孙 卡

（南昌航空大学 信息工程学院，南昌 330063）

该文针对严反馈非线性系统在Backstepping算法下进行优化。通过引入一个新的坐标变换，选择不同于传统反推控制算法的虚拟控制量。基于Backstepping的设计框架，逐层设计出了系统的虚拟控制律，继而推出实际的控制器。根据Lyapunov稳定性理论分析，系统各状态满足全局渐进稳定。最后对一个三阶的严反馈非线性系统进行数值仿真，发现系统在参考输入下，跟踪误差满足全局渐进稳定，并且相对于传统的反推控制算法，系统的收敛速度提高。证明了该方法可以提高系统的实时性。

非线性系统；严反馈；反推设计

严反馈非线性系统是下三角非线性系统的一种形式[1]，由于其在工程实践中有着广泛的适用范围，越来越受到科研人员的关注[2]。近年来，在严反馈非线性系统研究中取得了很多进展。如基于观测器的反推设计方法[3]、基于神经网络自适应设计方法[4]、基于模糊控制的自适应设计方法[5]、滑膜控制设计方法[6]等。以上方法在控制调节方面都取得了很好的效果，然后，大多数研究成果的控制算法的计算都相对复杂，在实际系统中，需要强大的运算芯片才能保证时效性。

反推控制对于严反馈形式的非线性系统控制有着良好的效果。文献[7]对反推控制的理论进行了研究，并将其应用在四旋翼飞行器控制器的设计之中。文献[8]针对纯反馈非线性系统进行了控制研究，使用了反步自适应控制和神经网络自适应控制算法分别对其进行了研究。文献[9]在神经网络设计方法的基础上引入观测器，对系统中的未知变量进行了处理。为了去除系统的摄动和外界的干扰，文献[10]提出了一种滑膜变结构的控制方法。文献[11]在滑膜控制的基础上，采用了动态二阶滑膜面的设计方法，以解决滑膜控制的抖振现象，得到了较好效果。文献[12]采用了反推控制技术，对随机纯反馈非线性系统，基于模糊控制理论提出了一种自适应模糊容错控制方案。文献[13]对一类严反馈控制系统，采用了神经网络动态面控制方法。文献[14]在神经网络研究的基础上进行了改进，采用串级控制的方法，以改善控制效果。文献[15]基于反推控制方法，对严反馈不确定控制系统进行了输出调节研究，最终得到全局渐进稳定。

本文针对一类严反馈非线性系统，利用一个坐标变换，基于反推设计的思想，研究了一类三角结构的非线性系统的镇定问题，通过设计出的虚拟控制律，进而得到控制器。该控制器保证系统跟踪误差全局渐进稳定，并且和传统的反推控制相比可以提高系统的收敛速度，在实际工程应用中可以提高系统的实时性，扩大了反推设计方法在实践中的应用范围。

1 反推控制

Backstepping最早在20世纪80年代由A.Saberi，P.V.Kokotovic和H.J.Sussmann等人对部分线性严格反馈的非线性系统研究时提出的。经过众多学者多年的深入研究，目前已经成为研究线性系统或者是非线性系统控制的重要的方法之一。Backstepping设计方法将Lyapunov稳定性判据和控制器的设计相结合，通过反向设计适用于高阶系统，且使系统控制器的设计过程结构化和系统化。它的设计过程为从系统最低阶次的方程开始，对每层子系统分别设计控制器，并引入虚拟控制的概念，设计满足条件的子控制器，最终设计出真正的控制器。其主要思想是将复杂的系统分解为阶数较低的子系统，通过对各个子系统构建Lyapunov函数和中间控制量进而推导出整个控制器。

考虑严格反馈的非线性系统为

式中：x=[x1，x2，…，xn]T为该系统各状态变量；u∈R为系统的输入；fi，gi为光滑的非线性函数，且gi≠0。

根据反推控制理论，我们利用各子系统的虚拟控制律，定义一个由各子系统组成的n维误差系统：

式中：ai为代表各阶子系统的虚拟控制律，根据系统稳定性的判断理论进行分析，设置虚拟控制律使每一层子系统的状态分量都渐进稳定。

步骤1对于第一层子系统，选取正定标量函数为

对标量函数进行求导运算：

步骤2对于第二层子系统，选取正定标量函数为

对标量函数进行求导：

步骤i对于第i层子系统，选取虚拟控制律

定义整个系统正定标量函数为

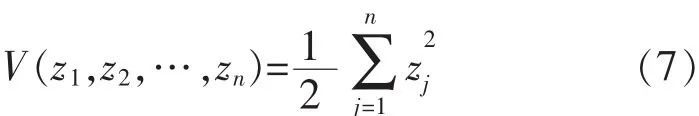
得到最终控制律为

由式（1）～式（4）可知：

从上述证明得到系统的标量函数是正定的，而标量函数的一阶导数为负定，根据李雅普诺夫稳定性判据可知整个系统全局渐进稳定。

2 问题描述

考虑如下一类严格反馈非线性系统：

式中：x =[x1，…，xn]T∈Rn是系统的状态；u∈R和y∈R分别为系统的输入和输出；函数fi：Ri→R，i=1，2，…，n-1是 C1未知的非线性函数，且满足fi（0）＝0。假设只有输出向量y是可测量的。

控制目标为在满足假设的条件时，设计的反推控制器能使严反馈非线性系统误差输出渐进稳定，即输出y能稳定地跟随参考信号yd。

3 控制器的设计

本文采用如下坐标变换：

式中：ai为第i个子系统的虚拟控制律。

此处控制器的设计，选择了与传统的反推控制方法不同的虚拟控制量参数。传统控制器将状态变量xi作为虚拟控制律的变量。而本文选择将x˙i-1作为虚拟控制律的变量，其中很大的部分计算都在运算的过程中，用所谓的空间来换时间的方法，凭借现在处理器强大的运算速度，可以提高系统的收敛速度，从而更好地满足工程实践中对实时性的要求。采用反推控制框架，控制器的设计分为n步：

步骤 1由式（10）、式（11）、式（12）可知：

假设虚拟控制律 a1为 a1=-c1z1+y˙d（c1为正的常数），则：

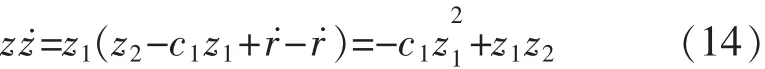
步骤 2由式（10）、式（12）可知：

步骤 i（3≤i≤n-1）

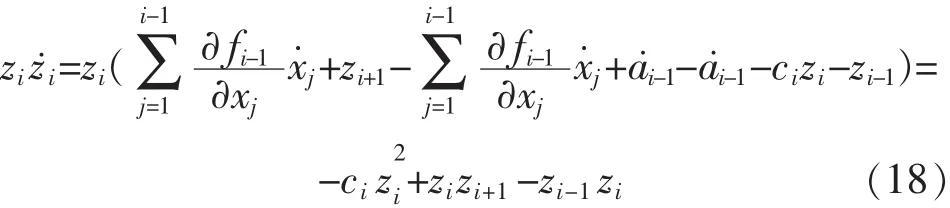
步骤 n由式（10）、式（11）、式（12）可知：

假设控制器u为

则

定理1对满足条件的该类严反馈非线性系统（10），采用控制律（20），在系统的平衡点跟踪误差全局渐进稳定。

证明选取下面的Lyapunov正定标量函数为

结合式（14）～式（21），对 v 进行求导：

由上式可知，当c1，c2，…，cn的值为正的常数时，正定标量函数的导数为负定，在满足函数fi：Ri→R，i=1，2，…，n-1 是 C1未知的非线性函数，且fi（0）=0时，系统在所设计的控制器下系统跟踪误差全局渐进稳定。

4 实例仿真

考虑一个三阶严格反馈非线性系统如下所示：

根据上文理论，初始值 x1（0）=0.7，x2（0）=-0.4，x3（0）=0.5，令 c1=c2=c3=1，参考输入 yd=sin（t）。

仿真结果如图1～图4所示。图1为系统在改进的反推控制算法下输出跟踪参考信号的轨迹变化曲线，可以看出，在该控制器的作用下，系统输出信号能够实现对参考信号的稳定跟踪，并且跟踪误差逐渐趋于零。图2为系统在传统的反推设计算法下输出跟踪参考信号的轨迹变化曲线。图3为改进型反推设计算法下的跟踪误差曲线。图4为传统反推算法下的跟踪误差曲线。其中，图1和图2中的标注R代表的是参考曲线，y代表在反推控制算法下的输出信号。

图1 改进后的参考跟踪性能Fig.1 Improved reference tracking performance

图2 传统反推控制下的跟踪性能Fig.2 Tracking performance under traditional backstepping control

从图3和图4的跟踪误差对比可以看出，传统的反推算法下，该仿真系统达到稳定的时间是在10 s左右，而采用改进的反推控制方法后，系统达到稳定的时间是6 s左右，改进型的收敛时间明显短于传统反推设计算法，即有效地提高系统的收敛速度。

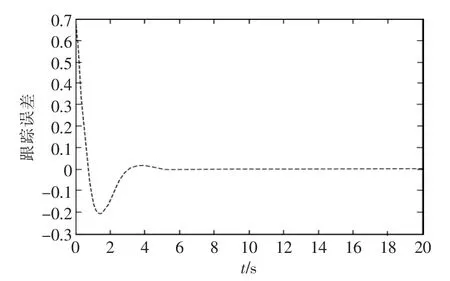
图3 改进后的跟踪误差Fig.3 Improved tracking error

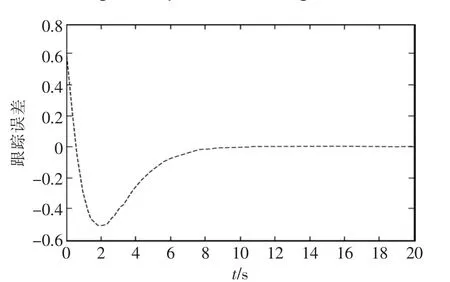
图4 传统反推控制下的误差Fig.4 Error of traditional backstepping control

5 结语

本文针对一类严格反馈控制系统的反推控制算法进行改进，基于反推控制的设计框架，引入一个新的变换矩阵，选择一个不同于传统反推控制的虚拟控制量，在系统跟踪误差满足全局渐进稳定的同时，相比于传统的反推控制，提高了系统的收敛速度。最后通过一个仿真试验验证了该改进型的反推控制可以提高系统的实时性。

[1] 孟桂芝.不确定非线性系统的输出调节及其应用[D].哈尔滨：哈尔滨工业大学，2013.

[2] Feng FeiJin，Bao zhu Guo.Lyapunov approach to output feedback stabilization fortheEuler-Bemoullibeam equation with boundary input disturbance[J].Automatica，2015，52（2）：95-102.

[3]Witt Thanom，Robert N.K.Loh.Observer-based nonlinear feedback controls for hearbeat ECG tracking syatems[J].Intelligent Control and Automation，2012（3）：251-261.

[4] Du Hongbin，ShaoHuihe，YaoPing jing.Adaptive neural network control for a class of low-triangular-structured nonlinear systems[J].IEEE Transactions on Neural Networks，2006，17（2）：509-514.

[5] Yong ming Li，Shao cheng Tong，Tie shan Li.Adaptive fuzzy backstepping control design for a lass of pure-feedback switched nonlinear systems[J].Nonlinear Analysis：Hybrid Systems，2015（16）：72-80.

[6] 梁勇，尚安利，邓方林.一类非线性系统的动态面二阶滑膜控制[J].控制理论与应用，2004，26（10）：1468-1522.

[7] 李天博.基于Backstepping方法的四旋翼无人机飞行器控制器设计[D].辽宁：东北大学，2013.

[8] 刘勇华.纯反馈非线性系统控制研究[D].广东：华南理工大学，2014.

[9] Honghong Wang，Bing Chen，Chong Lin，et al.Observer-based adaptive neural control for a class of nonlinear pure-feedback systems[J].Neurocomputing，2016，171（1）：1517-1523.

[10]Han Ho Choi.Output feedback stabilization of uncertain fuzzy systems using variable structure system approach[J].Fuzzy Sets and Systems.2008，16（3）：715-724.

[11]汪涛，胡剑波，李飞.一类纯反馈非线性系统的反推近似滑膜控制[J].计算机仿真，2015，33（9）：358-363.

[12]Shuai Sui，Shaocheng Tong，Yongming Li.Fuzzy adaptive faulttoleranttracking controlofMIMO stochastic pure-feedback nonlinear systems with actuator failure[J].Journal of the Franklin Institute，2014，351（6）：3424-3444.

[13]Xu，B.Composite neural dynamic surface control of a class of uncertain nonlinear systems in strict-feedback form[J].Cybernetics，IEEE Transactions on，2014，44（12）：2626-2634.

[14]王良勇.一类严反馈非线性系统的神经网络串级控制及应用[J].电机与控制学报，2013，17（12）：106-112.

[15]Riccardo Marino，Cristiano Maria Verrelli.A global feedback output regulating control for uncertain systems in strict feedback form[J].Systems&Control Letters，2009，58（9）：682-690.

Optimal of Backstepping Control for Strict-feedback Nonlinear Systems

PAN Jian-xiong，SUN Ka

（College of Information Engineering，Nanchang Hangkong University，Nanchang 330063，China）

In this paper，aiming at optimized the Backstepping control for strict-feedback nonlinear system.By introducing a novel coordinate transformation，select different from traditional backstepping control algorithm of virtual control volume.Based on backstepping framework，the virtual control law of the systems is designed，then introduced the actual controller.It finds that the global asymptotic stability can be achieved when the tracking error of the system is under the control algorithm by analyzing the Lyapunov stability theory.By the end，numerical simulation is carried out on a three order strict-feedback nonlinear system.Under the reference input，the tracking error is globally asymptotically stable and compared with the traditional backstepping control algorithm，the convergence rate of the system is improved，which provides an effective method for improving the real-time performance of system.

nonlinear systems；strict-feedback systems；backstepping

TP273

A

1001-9944（2017）11-0056-04

10.19557/j.cnki.1001-9944.2017.11.013

2017-04-07；

2017-07-24

潘建雄（1992—），男，在读硕士研究生，研究方向为非线性控制理论研究与嵌入式开发；孙卡（1982—），男，博士，副教授，研究方向为飞行仿真与图形学。