基于Toeplitz矩阵的MIMO雷达DOA估计∗

吴 萌

（91404部队 秦皇岛 066000）

基于Toeplitz矩阵的MIMO雷达DOA估计∗

吴 萌

（91404部队 秦皇岛 066000）

多输入多输出（Multiple Input Multiple Output，MIMO）雷达在目标识别和参数估计方面具有独到的优势，DOA估计是MIMO雷达参数估计的重要内容。从MIMO雷达接收信号模型出发，推导了发射正交信号，在接收端匹配滤波的过程，提出了一种接收信号协方差toeplitz矩阵的构造方法以实现信号解相干。基于高分辨子空间MUSIC方法对算法估计性能进行了对比研究，仿真结果表明，在相同的条件下所提出的算法能够实现低信噪比条件下目标信号解相干，可以估计相邻目标方位，具有较好的估计能力。

MIMO雷达；DOA估计；toeplitz矩阵

1 引言

多输入多输出（Multiple Input Multiple Out⁃put，MIMO）雷达是近年提出的一种新体制雷达，其显著特点是具有空间分集和信号分集特征。MIMO雷达能够抑制目标信号闪烁和信道衰落的影响，扩展雷达有效阵列孔径，增大系统自由度，在目标识别及参数估计方面具有独到的优势［1～3］。

确定目标的方位，即回波到达方位（DOA）估计，是MIMO雷达目标参数估计的主要内容，受到研究者极大关注，由此发展了多种估计方法。传统的常规波束形成方法受瑞利限（Rayleigh Limita⁃tion）制约，无法分辨位于同一波束内的目标，其估计能力有限。而后发展的高分辨率空间谱估计方法突破了瑞利限的限制，具有多信号同时测向、超分辨率、测向精度高等显著优点，已成为DOA估计的主要方法。其中的子空间类算法，如经典的MU⁃SIC、ESPRIT等算法因计算方便、估计性能优越而获得广泛的应用［4～6］。子空间类算法的原理是将接收信号相关矩阵分解为信号子空间和噪声子空间，利用信号及噪声子空间的正交特性进行DOA估计。子空间类算法在非相干信号环境中有很好的估计性能，但在相干信号环境中，由于接收信号相关矩阵秩的退化，实际目标方向向量张成的信号子空间与阵列数据协方差矩阵推得的信号子空间不一致，实际方向向量张成的信号子空间与噪声子空间不再正交，导致子空间类算法性能下降甚至完全失效［7～8］。

针对这一问题，众多学者提出了许多接收信号解相干方法，来弥补子空间类DOA估计方法的缺陷，主要包括降维与非降维两类方法［9～11］。采用降维类方法如空间平滑法解相干时损失了雷达阵列的物理孔径，导致目标分辨力下降。而非降维类方法避免这一问题，且没有特定条件限制，成为解相干处理的重要方法。本文分析了MIMO雷达信号模型的特点，提出一种非降维类Toeplitz矩阵解相干算法，将其应用于MIMO雷达DOA估计，并基于子空间类算法分析研究了Toeplitz矩阵方法的性能。

2 MIMO雷达信号模型

作如下假设：

1）接收的目标信号为窄带信号；

2）接收基阵位于信号源的远场，可近似认为接收到的信号为平面波；

3）接收阵元的几何尺寸远小于入射平面波的波长λ，且阵元无指向性，可以近似认为接收阵元是点元，空间增益为1；

4）各接收阵元相互独立，各阵元噪声互不相关。

讨论MIMO雷达发射阵和接收阵均为等距线阵的情况，设发射阵和接收阵阵元数分别为N和M，阵元间距分别为dt和dr。为保证接收信号不产生分辨模糊，接收阵元间距满足半波长条件，即dr≤λ/2，其中λ为载波波长，本文取 dr=λ/2。

各发射阵元发射互相独立的窄带信号：

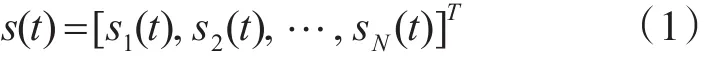
令第一个发射阵元为参考发射阵元，则目标k处发射导向矢量为

其中，θk为目标k相对发射阵列法线方向的夹角。

ai(θk)为发射导向矢量的第i个元素，目标k处叠加信号为

假设目标k散射系数为常数βk，则接收阵列各阵元接收到散射信号为

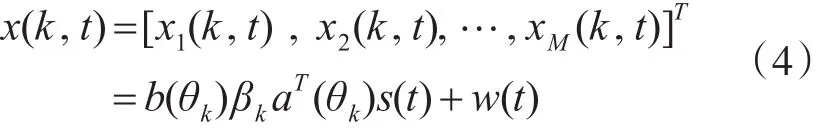
其中，b(θk)为目标k的接收导向矢量：

w(t)为接收阵列噪声矢量：

对于存在K个目标的情况，接收信号即为

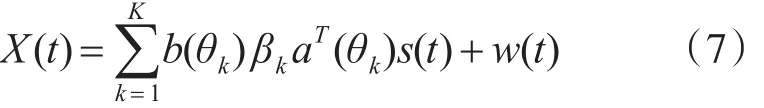
令L为快拍数，则l快拍时刻式（7）采样的信号模型为

式（8）写成矩阵形式为

其中，S∈CN×L为正交发射信号阵列，满足SSH=IN，IN为 N×N维单位矩阵；W∈CM×L为复高斯白噪声。

将各接收阵元的接收信号与N个发射信号进行匹配滤波处理，整个匹配滤波器组的输出信号矩阵为

其中，V=∑WSH/L。将式（10）中的矩阵Y以向量的形式给出，可以表示为

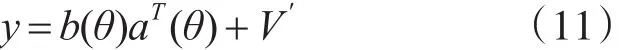
其中，b(θ)∈CM×K是接收导向矢量矩阵，a(θ)∈CN×K是发射导向矢量矩阵。

3 Toeplitz方法

采用前向平滑的方法计算接收阵列相关矩阵

理想情况下，均匀线阵接收信号协方差矩阵具有明显的Toeplitz性质，矩阵具有共轭对称性，但在实际中，由于快拍数的有限性和噪声的干扰或者多径干扰，这种性质往往受到破坏，尤其在低信噪比情况下，接收信号协方差矩阵一般只是对角占优。可以通过对矩阵原有数据的Toeplitz化构造新的协方差矩阵以接近真实的协方差矩阵，从而实现信号的解相干。

取接收阵列第m个阵元为参考阵元，将其它各阵元接收信号与参考阵元进行相关运算，得：

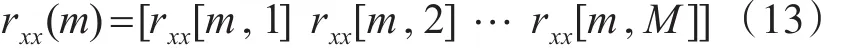
利用rxx(m)为行构造Toeplitz矩阵 RT(m)，其上三角元素为

下三角元素为

则所构造的Toeplitz矩阵为

为了更有效利用接收阵列信号，分别以各接收阵元为参考阵元，采用以上方法构造Toeplitz矩阵并进行平均，则算法性能会更好，即：

将所构造的Toeplitz矩阵作为接收信号协方差矩阵的似然估计，采用子空间类方法进行DOA估计，基于Toeplitz矩阵进行MUSIC空间谱估计公式为

式中，a(θ)为接收阵列在θ方位上的导向矢量，表征信号子空间；Vn为对矩阵RT进行特征分解后张成的噪声子空间。在来波方向接收导向矢量与噪声子空间矩阵正交，上式分母取极小值，MUSIC空间谱产生尖峰值，遍历角度值θ，搜索空间谱峰值则可获得信号源方位。

4 仿真实验与分析［12～15］

为了验证算法的有效性，分别采用Toeplitz矩阵和空间平滑算法对接收信号协方差矩阵进行预处理，并运用子空间类MUSIC算法进行MIMO雷达DOA谱估计，将此两种算法与传统MUSIC算法进行对比分析。

采用6个发射阵元，10个接收阵元，接收阵列为等距线阵，接收阵元间隔半波长，快拍数100。空间平滑算法子阵阵元数5，则子阵个数为6。存在 5个目标，波达方向分别为-20°、0°、5°、10°和20°。信噪比SNR=10dB时，采用传统MUSIC算法、Toeplitz-MUSIC算法和FBSS-MUSIC算法分别进行波达方向估计，蒙特卡罗仿真次数为200次，仿真结果如图1所示，图中虚线为MUSIC算法估计空间谱，实线为Toeplitz-MUSIC算法估计空间谱。

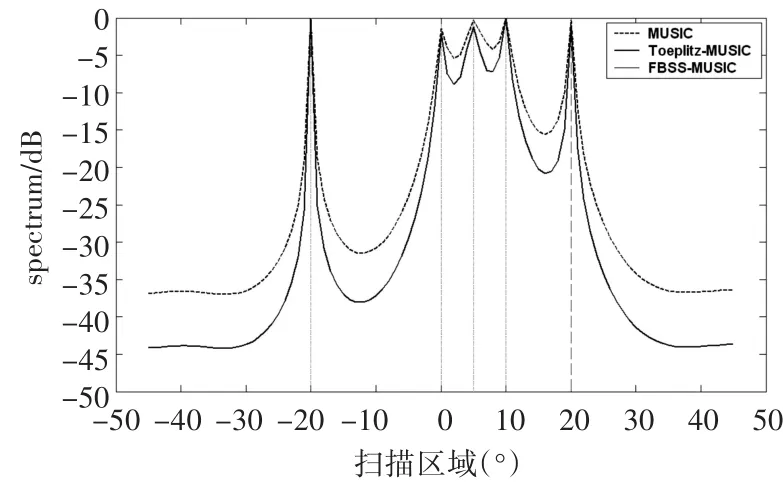
图1 MUSIC/Toeplitz-MUSIC/FBSS-MUSIC波达方向估计空间谱（目标数5，SNR=10）

由仿真过程知在此仿真条件下，空间平滑算法失效，这主要是由于空间平滑算法引起阵列孔径损失，造成阵列自由度降低、可分辨目标数目减少。MUSIC方法及改进的Toeplitz-MUSIC方法分辨力较高，理论上可识别与接收阵元几乎相当的目标数目，Toeplitz矩阵方法没有造成阵列孔径损失。由图1可见，MUSIC方法及Toeplitz-MUSIC方法在目标方位附近均产生明显的谱峰，但后者空间谱旁瓣较MUSIC方法更低，在目标方位估计上更具优势。目标方位接近时，Toeplitz-MUSIC方法谱峰和峰谷特征较明显，表明此种方法成功实现了相邻目标回波信号的解相干，在DOA估计上更具优势。

采用4个发射阵元，10个接收阵元等距线阵，目标方位在0°和5°，快拍数80，蒙特卡罗仿真次数为200次，统计三种DOA估计算法的均方根误差随信噪比变化，取0°目标曲线如图2所示。可以看到，各算法均方根误差随信噪比的增大总体呈减小的趋势，随信噪比增加DOA估计精度不断提高。总体来说看，Toeplitz-MUSIC方法具有较小的估计均方根误差，表明这一算法具有较高的估计精度。低信噪比时这一特征尤其显著，仿真条件相同时，同一信噪比下Toeplitz-MUSIC方法精度较另外两种有最高的估计精度。表明Toeplitz-MUSIC方法在低信噪比环境下能够实现相干信号DOA估计，且具有较高估计精度。

图2 MUSIC/Toeplitz-MUSIC/FBSS-MUSIC波达方向估计均方根误差随信噪比变化曲线（阵元数10，快拍数80）

图3为采用4个发射阵元，10个接收阵元等距线阵，目标方位在0°和5°，信噪比10，蒙特卡罗仿真次数为200次，三种估计算法的均方根误差随快拍数变化曲线，取0°方位目标仿真结果。随快拍数增大，各方法估计精度不断提高，且当快拍数大于一定值后对各算法均方误差影响降低，表明增加接收信号数据量可以提高MIMO雷达DOA估计精度，但随其增加对估计精度的作用减弱，且使用要求也对接收信号数据量产生限制。由图可见，To⁃eplitz-MUSIC算法的估计精度高于另外两种算法，此算法可以在较少的接收信号数据量情况下获得需要的估计性能。

图3 MUSIC/Toeplitz-MUSIC/FBSS-MUSIC波达方向估计均方误差随快拍数变化曲线（阵元数10，SNR=10）

图4 为采用4个发射阵元，目标方位在0°和5°，快拍数80，蒙特卡罗仿真次数为200次，三种估计算法的均方根误差随阵元数变化曲线，取0°目标结果。由图可见，Toeplitz-MUSIC算法的估计精度高于空间平滑FBSS-MUSIC算法及传统MUSIC算法，随阵元数增大，各方法估计精度不断提高。

图4 MUSIC/Toeplitz-MUSIC/FBSS-MUSIC波达方向估计均方误差随阵元数变化曲线（快拍数80，SNR=10）

由估计均方根误差分析过程可见，对空间方位相邻目标估计方面，三种算法中Toeplitz-MUSIC具有最高的精度，Toeplitz-MUSIC算法能成功实现对低信噪比方位相邻目标进行精确估计。

5 结语

本文针对均匀线阵MIMO雷达，建立了雷达的匹配滤波信号模型，采用一种Toeplitz矩阵构造方法，结合MUSIC算法对MIMO雷达DOA估计性能进行了对比研究。仿真结果表明，所采用的To⁃eplitz矩阵构造方法能够在低信噪比条件下实现相邻角度目标的估计，具有较高的估计精度和性能。

［1］Fishler E，Haimovich A，Blum R.Spatial Diversity in Ra⁃dars-models and Detection Performance［J］.IEEE Trans⁃actions on Signal Processing，2006，54（3）：823-838.

［2］Bekkerman I，Tabrikian J.Target Detection and Localiza⁃tion Using MIMO Radar and Sonars［J］.IEEE Transac⁃tions on Signal Processing，2006，54（10）：3873-3883.

［3］Bliss D W，Forsythe K W.Multiple-input Multiple-Output（MIMO）Radar and Imaging：Degrees of Freedom and Resolution［C］//Conference Record of the Thirty-Seventh Asilomar Conference on Signals，Systems and Computers，Pacific Grove，CA，2003：54-59.

［4］Rao B D，Hari K V S.Performance analysis of Root-MIU⁃SIC［J］.IEEE Trans.on Acoustic，Speech and Signal Pro⁃cessing，1989，37（12）：1939-1949.

［5］Evans J E，Johnson J R.High resolution angular spectrum estimation techniques for terrain scattering analysis and angle of arrival estimation［C］//Proc.The First ASSP Workshop Suectral Estimationn，1981：134-139.

［6］Roy R，Kailath T.ESPRIT-a subspace rotation approach to estimation of parameters of cissoids in noise［J］.IEEE Trans.on ASSP，1986，34（10）：1340-1342.

［7］许红波，王怀军，陆珉，等.一种新的MIMO雷达DOA估计方法［J］.国防科技大学学报，2009，31（3）：92-96.XU Hongbo，WANG Huaijun，LU Min，et al.A New Algo⁃rithm on Estimation of DOA Using MIMO Radar［J］.Jour⁃nal of National University of Defense Technology，2009，31（3）：92-96.

［8］陈晨，张小飞，李建峰.波形相关矩阵未知情况下单基地MIMO雷达中一种改进MUSIC的DOA估计算法［J］.电子与信息学报，2012，V34（12）：2966-2971.CHEN Chen，ZHANG Xiaofei，LI Jianfeng.An Improved MUSIC DOA Estimation Algorithm for Monostatic MIMO Radar without Knowledge of Waveforms Correlated Matrix［J］.Journal of Electronics&Information Technology，2012，34（12）：2966-2971.

［9］王克让，何劲，贺亚鹏，等.MIMO雷达DOD和DOA联合估计算法：RTR-ESPRIT［J］.航空学报，2012，34（5）：893-901.WANG Kerang，HE Jing，HE Yapeng，et al.RTR-ESPRIT for joint DOD and DOA estimation for MIMO radars.Acta Aeronauticaet AstronauticaSinica，2012，33（5）：893-901.

［10］杨巍，刘峥.MIMO雷达波达方向估计的性能分析［J］.西安电子科技大学学报（自然科学版），2009，36（5）：819-824.YANG Wei，LIU Zheng.Performance analysis of MIMO Radar DOA Estimation［J］.Journal of Xidian University，2009，36（5）：819-824.

［11］陈绍炜，魏盈盈，冯晓毅.基于SVD和Toeplitz的高效DOA估计算法［J］.西北工业大学学报，2010，28（6）：883-886.CHEN Shaowei，WEI Yingying，FENG Xiaoyi.A New and Efficient TSVD Algorithm for Estimating DOA（Di⁃rection of Arrival）［J］.Journal of Northwestern Polytech⁃nical University，2010，28（6）：883-886.

［12］张娟，张林让，刘楠，等.一种有效的MIMO雷达相干信源波达方向估计方法［J］.电子学报，2011，39（3）：680-684.ZHANG Juan，ZHANG Linrang，LIU Nan，et al.An Effi⁃cient DOA Estimation Algorithm of Coherent Sources for MIMO Radar［J］.Acta Electronica Sinica，2011，39（3）：680-684.

［13］韩勇，乔晓林，金铭，等.基于Toeplitz矩阵的波束空间新算法［J］.电波科学学报，2009，24（4）：667-671.HAN Yong，QIAO Xiaolin，JIN Ming，et al.New Beam-space Algorithm Based on Toeplitz Matrix［J］.Chinese Journal of Radio Science，2009，24（4）：667-671.

［14］刘玲，刘晓明，曾浩.基于MATLAB的阵列信号处理仿真方法［J］.系统仿真学报，2008，20（13）：3548-3552.LIU Ling，LIU Xiaoming，ZENG Hao.Array Signal Pro⁃cessing Simulation Based on MATLAB［J］.Journal of System Simulation，2008，20（13）：3548-3552.

［15］Bassem R.Mahafza，Atef Z.Elsherbeni著，朱国富，黄晓涛，黎向阳，李悦丽译.雷达系统设计MATLAB仿真［M］.北京：电子工业出版社，2009.Bassem R.Mahafza，Atef Z.Elsherbeni.MATLAB Simula⁃tions for Radar System Design［M］.Beijing：Publishing House of Electronics Industry，2009.

DOA Estimation Based on Toeplitz Matrix for MIMO Radar

WU Meng
（No.91404 Troops of PLA，Qinhuangdao 066000）

Direction of arrival（DOA）estimation is an important aspect of MIMO radar，which have significant advantages in target detection and parameter estimation.Commencing with signal model of MIMO radar，the process of filtering in receiver was de⁃duced by transmitting orthogonal signals and a construction method of covariance matrix of

signals was proposed to realize signals decoherence.Based on the MUSIC algorithm，the DOA estimation performances were studied contrastively，the result indi⁃cated that the toeplitz-music algorithm proposed could estimate the direction of closer target and had a high accuracy under same conditions.The algorithm proposed gets good decoherence effect and estimation performances in low signal-to-noise ratio condi⁃tions.

MIMO radar，DOA estimation，toeplitz matrix

Class Number TN957

TN957

10.3969/j.issn.1672-9722.2017.12.015

2017年6月2日，

2017年7月25日

吴萌，男，助理工程师，研究方向：作战指挥系统试验。