MMTD算法在蚁群算法中的应用和研究∗

朱俚治

（南京航空航天大学信息中心 南京 210016）

MMTD算法在蚁群算法中的应用和研究∗

朱俚治

（南京航空航天大学信息中心 南京 210016）

当今的计算机专家和工程师们为了提高机器的智能性，因此在各科的领域中开发出了众多的智能算法，这些算法主要用于解决最优解问题。蚁群算法是智能算法中的一种，该算法采用由个体的最优解从而引导产生整体的最优解。在蚁群算法中当蚂蚁寻找最短路径的时候，利用信息素浓度的不同和挥发系数的不同强度为蚁群寻找最优解提供了重要依据。论文根据已有的蚁群算法，提出了使用MMTD算法对蚁群信息素的挥发系数进行衡量和计算，将MMTD算法在蚁群算法中进行应用是该文主要创新之处。

蚁群算法；MMTD；信息素；挥发系数；智能性

1 引言

群集智能作为一种新兴的演化计算技术已引起了越来越多相关研究人员的关注［7～9］。蚁群算法是一种智能性的仿生物学算法，该算法最早由M.Dorigo学者提出，这以后蚁群算法逐步引了起人们的重视，人们将该算法在诸多领域中进行了应用。当今的蚁群算法主要有以下几个方面的应用，经典旅行商问题，二次分配的问题，车间任务调度问题等一系列方面的应用［7～8］。蚁群算法除了在以上几个方面应用之外，还能够在数据挖掘中的分类和聚类等方面进行应用。蚁群算法在这些领域方面的应用都获得了成功，其主要原因是蚂蚁个体的对不同环境的具有适应性以及蚂蚁个体之间的协作性的特点，这些都是蚁群算法在各个科研领域获得成功应用的重要因素。本文根据蚁群算法的特点，将MMTD算法在蚂蚁搜索最短路径时候产生的信息素强度和信息素的挥发性上进行衡量和应用是本文的主要创新点。

2 蚁群算法的基本原理

2.1 蚁群算法的介绍

蚁群算法最初的目的是帮助人们去理解蚂蚁这类物种的复杂行为。蚁群算法出现之后不久便引起了数学家，计算机专家和工程师们的注意，他们把超越生物本身的模型转换成了一项有用的优化和控制算法——蚁群算法，也称为蚁群系统。在蚁算法中的个体具有以下的特性［5～7］：

1）蚁群的个体的行为极为简单，通过信息的传递个体之间的协作，能够完成复杂的任务。

2）蚁群的个体具有一定记忆力，一定的智能性。

3）蚁群的个体能够适应周围环境的变化，具有一定的适应性。

当蚁群寻找最短路径的时候，在经过的路径上都会留下一种叫做信息素的物质，这种物质具有挥发性。蚁群的个体与个体之间能够感知信息素的这种物质，它们通过这种物质的挥发性进行信息传递和信息交流。寻找最短路径的蚁群总是向着信息素浓度最强和最高的方向运动，信息浓度越高则这条路径中聚集的蚂蚁就越多，路径中的蚂蚁越多，越发增加该路径的信息素强度，这样又吸引了更多的蚂蚁来到这条路径之中，从而使得整个蚁群最终能够发现蚁巢到食物之间的最短路径。

2.2 蚁群的算法的简要分析

蚁群是一个种群，是一个群体，因此当蚁群在寻找到达食物的最短路径的时候并不是个体行为，而是一个群体的行为。蚁群算法初始的状态是首先通过蚂蚁的个体去寻找最短路径，从而再使得整个蚁群都找到最优解和最短路径。在寻找最短路径的时候，蚁群中的蚂蚁个体在时间上并没有先后，而是在同一个时间点内可以有若干蚂蚁同时寻找通往目的地的最短路径。

当蚁群寻找最短路径的时候有两个重要因素：1）蚂蚁个体对环境变化的适应性；2）蚂蚁个体与个体之间相互交换信息，及蚂蚁之间的协作性。在蚁群寻找最短路径的时候，每一条路径上都有一定数量的蚁群在活动。蚂蚁之间存在协作性、并行性和个体的适应性等这些特点，能够使得各条路径中的蚁群通过信息素的传递从而使得整个蚁群都能够找到到达目的地的最短路径。基于上述蚁群算法的特点，蚁算法在寻找最短路径的时候具有较高的效率，缩短了算法求解的时间。

3 蚁群的信息素以及信息素的挥发

3.1 蚁群的信息素

在蚁群出发之前路径上的信息素浓度值均为0，当蚁群开始搜索达到食物的最短路径的时候就会在路径上留下不同浓度的信息素，这些信息素中某些浓度会强些，而某些信息素的浓度则会弱些。由于各条路径上信息素强度的不同，从而决定着蚁群在寻找食物时有不同的运动方向，但信息素浓度将随着时间的变化而变化，信息素浓度的变弱或变强能够不断地影响蚁群的活动。

3.2 蚁群信息素的挥发性

在蚁群搜索最短路径的过程中，整个蚁群都处于不断的运动之中。如果某条路径中的蚂蚁数量较多，那么在该路径中留下信息素浓度的较强，当路径中的蚂蚁数量较少或十分少的时候则这时蚂蚁在路径上留下信息素浓度的较弱或十分的弱。信息素浓度的挥发和变化是蚁群在不同路径活动中产生的结果，信息素浓度不断的变化将引导整个蚁群去寻找最短路径，是蚁群寻找最短路径的关键因素。

蚁群在路径上留下的信息素具有挥发性，信息素的挥发性实现了蚁群之间信息的传递性和进行蚁群之间的交流。信息素的挥发性是蚁群个体与个体之间的一种交流方式和交流手段，如果没有信息素的挥发性，那么整个蚁群就缺少必要的信息交流工具。

在通往目的地的各条路径中，如果某条路径之中蚂蚁数量越多，此时信息素浓度越强则信息素的挥发因子就越大，发挥因子越大那么该路径中蚂蚁的数量就会变多变大。如果某条路径中蚂蚁的数量在变少的过程中，那么该条路径中的信息素浓度会逐步变弱，挥发因子也会相应的变小，变弱。因此某条路径中信息素的浓度变强或变弱是由于路径中的蚁群数量在发生变化，然而路径中蚁群数量的变化往往又确定于信息素浓度和信息素挥发因子的大小。

4 蚁群算法的计算公式及其分析

4.1 蚁群信息素的计算公式

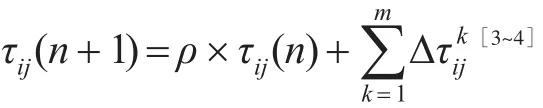
m是蚂蚁中的个数，n为迭代的次数，i为蚂蚁所在的位置，j为蚂蚁所能达到的位置，∆为蚂蚁可以到达位置的集合，ηij为启发信息，这里为由i到 j的路径的能见度。τij为路径i到 j的路径的信息素强度。∆为蚂蚁k由i到 j的路径上留下的信息素数量。α为路径权，β为启发性信息的权，ρ为路径上信息素数量的蒸发系数，Q信息素质量系数［3～4］。

4.2 信息素计算公式的分析

每条路径中的信息素浓度会随着时间增强或减弱。信息素浓度最高最强的路径往往是蚁群算法中选择的路径。

现在有N条路径，在N条路径中的信息素浓度各不相同。如果某条路径上信息素浓度变强，则蚁群向这条路径运动。当有蚂蚁向这条路径运动，那么该路径信息素的浓度会逐步变大变强的值会逐步变大，信息素的挥发性就会逐步增强，因此此时τij的值也将变大。如果某条路径上信息素浓度在变弱的过程中，那么这条路径蚁群中的数量将越来越少这时的值会逐步变小。由于该条路径中的蚂蚁数量在逐渐减少，那么τij的值也将逐步变小，那么这条路径中的τij会逐步接近于0。

蚁群中的蚂蚁在选择路径的时候，协作性体现在当个别蚂蚁个体在选择了适当路径的时候，能够通过蚁群信息素能够使得蚂蚁个体与个体进行信息交流，使得别的蚂蚁也能够选择相同的路径，从而实现蚁群之间相互的协作性。在蚁群选择路径的过程中，使得信息素浓度τij值变大的路径被选择的几率较大，相反的信息素浓度τij值变小变弱的路径被选着几率将十分的小，因此信息素的作用在蚁群的协作性方面起到了关键性的作用。

5 MMTD算法技术简介

5.1 中介真值程度度量知识简介

中介逻辑将事物的属性描述成三种状态，事物属性的两个对立面和对立面的中间过渡状态。在中介真值程度度量方法中，提出了事物超态属性概念，该方法符合中介思想事物的属性并且被划分为五种状态：事物的两个对立面，对立面的中间过渡状态和事物超态对立面［1～2］。这里用符号表示为～P，P与╕P，超态+p与超态╕+p。现用数轴将以上的描述的概念表达如下［1～2］：

图1 中介真值程度度量一维函数图

对数轴 y=f(x)表示的含义有以下说明［1～2］：

数轴上用符号P与╕P分别表示事物对立面的两个属性，符号～P表示反对对立面的中间过渡状态达事物的属性。

1）如果数轴上数值点的位置逐步接近P，则事物A所具有P的属性逐步增强。

2）如果该数值点的位置落在真值╕P和 P的取范围之间，则事物A的属性就部分地具有╕P的属性，同时又部分地具有P的属性。

3）如果数轴上数值点的位置逐步接近╕P，则事物A所具有╕P的属性逐步增强。

5.2 中介真值程度度量中的距离比率函数

在中介真值程度度量的方法中，数轴上某数值点通过距离比率函数来计算事物所具有属性的强弱。

定理1 给定 y=f(x)∈f(X)，ξ(h(y))=h(y)，则有［1～2］

1）当 αF+εF＜y＜αT-εT时 ，gT(x)∈(0，1) ，gF(x)∈(0，1)。

2）当 y＞αT+εT时，gT(x)＞1；当 y＜αF-εF时，gF(x)＞1。

3）当 y＜αF-εF时，gT(x)＜0 ；当 y＞αT+εT时，gF(x)＜0。

4）gT(x)+gF(x)=1。

（1）相对于 P 的距离比率函数［1～2］

6 MMTD方法的应用

6.1 关于蚁群信息素浓度公式的描述

函数：f(x)=所有目前最新的信息素强度-已知的最大信息素强度

τij表示信息素强度，t+1表示当前时刻，t表示前一时刻。

τij(t+1)表示当前时刻的信息素强度及所有最新的信息素强度，τij(t)表示前一时刻的信息素强度及已知的最大信息素强度。函数：

分析和讨论：

1）τij(t+1)＞ τij(t)

当τij(t+1)＞τij(t)的时候：如果当前时刻的信息素强度τij(t+1)与前一个时刻的信息素强度τij(t)的差值越大，则信息素的强度在增强，并且这时路径的信息素浓度会逐步变大变强。当τij(t+1)在变大中，根据蚁群算法的特点可知蚁群总是向信息素浓度变大的路径运动。当该条路蚂蚁的数量就越大，则某条路径信息素的浓度越大，该条路径被选择作为最短路径的可能性就越大。

2） τij(t+1)＜ τij(t)

当τij(t+1)＜τij(t)的时候：如果当前时刻的信息素强度τij(t+1)与前一个时刻的信息素强度τij(t)的差值越大，则信息素的强度在减弱，并且这时路径的信息素浓度会逐步变小变弱。当τij(t+1)也在变小中，根据蚁群算法的特点可知蚁群总是向信息素浓度变大的路径运动，如果某条路径蚁群产生的信息素浓度逐步的变小，该路径被蚁群舍弃的可能性很大，该路径不是蚁群寻找的最短路径。

6.2 中介对信息素浓度的描述

以下用中介真值程度度量方法对蚁群产生的信息素浓度做以下的研究：

数轴 y=f(x)上有P，～P，╕P三个数据区域，P代表信息素浓度增强，╕P代表信息素浓度减弱，～P代表信息素浓度半强半弱。

6.3 距离比率函数

从数轴上 y=f(x)可以知道，在数轴上以～P为对称中心，左右分别为╕P和P。

图2 中介真值程度度量一维函数的应用

y=f(x)的 值 落 在 三 个 值 域 范 围（αr+εr，αl- εl），（αr-εr，αr+ εr）（αl- εl，αl+ εl）。 ～P 的区域 为（ αr+εr，αl-εl），╕P 的 区 域 为（αr-εr，αr+εr），P 的区域为（αl-εl，αl+εl）。 P 的真值为1，╕P的真值为0。

相对于P的距离比率函数

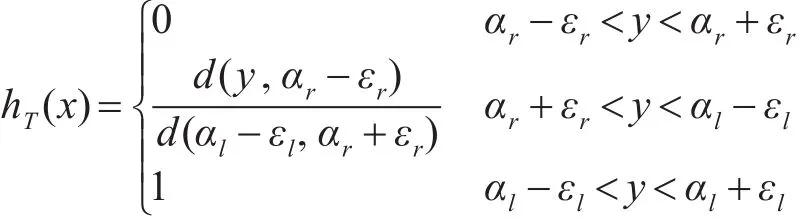
通过距离比率函数hT(x)对y值的计算，如果有：

1）若函数 hT(x)=1，y值落在区域（αl-εl，αl+εl），则此时信息素强度增强，其真值为1。

2）若函数 hT(x)=0，y值落在区域（αr-εr，αr+εr），则此时信息素强度减弱，其真值为0。

7 结语

蚁群算法是一种仿生物学的智能性算法，该算法主要解决的问题是寻找到达食物的最短路径。蚁群算法的特点是从有个体的最优解从而引导整个群体的最优解，该算法有较广泛的应用性，在诸多领域有着广泛的应用。本文根据蚁群在寻找最短路径时候蚂蚁具有的适应性和协作性的特点，提出了将具有模糊思想的MMTD算法在蚁群寻找最短路径中进行首次应用。将MMTD算法在蚁群算法中进行应用是本文的主要创新点，这也是将具有模糊思想算法在蚁群算法中的应用尝试。

［1］洪龙，肖奚安，朱梧槚.中介真值程度的度量及其应用（I）［J］.计算机学报，2006（12）：2186-2193.HONG Long，XIAO Xian，ZHU Wujia.Measure of Medi⁃um Truth Scale and Its Application（I）［J］.Chinese Jour⁃nal of computers，2006（12）：2186-2193.

［2］朱梧槚，肖奚安.数学基础与模糊数学基础［J］.自然杂志，1984（10）：723-726，800.ZHU Wujia，XIAO Xian.Foundations of Classical Mathe⁃matics and Fuzzy Mathematics［J］.Nature Magazine，1984（10）：723-726，800.

［3］吴庆洪，张颖，马宗民.蚁群算法综述［J］.微型计算机信息，2011，27（3）：1-5.WU Qinghong，ZHANG Ying，MA Zongmin.An overview of the ant colony algorithm［J］.Micro computer informa⁃tion，2011，27（3）：1-5.

［4］胡小兵，袁锐，黄席樾，等.蚁群算法原理的仿真研究［J］.计算机仿真，2004，21（8）：125-127.HU Xiaobing，YUAN Rui，HUANG Yuexi，et al.Research simulation of ant colony algorithm principle［J］.Computer Simulation，2004，21（8）：125-127.

［5］程艳燕.蚁群算法基本原理及其应用综述［J］.科技创业月刊，2011（4）：117-120.CHENG Yanyan.Basic principle of ant colony algorithm and its application in［J］.Science and technology entre⁃preneurship monthly，2011（4）：117-120.

［6］李开荣，陈宏建，陈崚.一种动态自适应蚁群算法［J］.计算机工程与应用，2004（29）：149-152.LI Kairong，CHEN Hongjian，CHEN Ling.A dynamic adaptive ant colony algorithm［J］.Computer Engineering and Applications，2004（29）：149-152.

［7］黄挚雄，张登科，黎群辉.蚁群算法及其改进形式综述［J］.计算技术与自动化，2006，25（3）：35-38.HUANG Zhiqiong，ZHANG Dengke，LI Qunfai.Ant colo⁃ny algorithm and its improved form review［J］.Journal of computing and automation，2006，25（3）：35-38.

［8］冯宝华.蚁群优化算法的原理改进［J］.计算机与信息技术，2007（31）：94-96.FENG Baohua.Principle ACO Improvement［J］.Computer and Information Technology，2007（31）：94-96.

［9］冯月华，陈州吉.基于群体智能的蚁群算法原理及应用研究［J］.兰州文理学院学报（自然科学版），2014，28（2）：58-62.FENG Yuehua，CHEN Zhoujie.The principle and applica⁃tion of ant colony algorithm based on swarm intelligence research［J］.Journal of lan zhou journals of liberal arts college（natural science edition），2014，28（2）：58-62.

［10］朱树人，匡芳君，王艳华.基于粒度原理的蚁群聚类算法［J］.计算机工程，2005，31（23）：162-166.ZHU Shuren，KUANG Fangjun，WANG Yanhua.granu⁃larity based on ant colony clustering algorithm principle［J］.Computer Engineering，2005，31（23）：162-166.

［11］刘士新，宋建海，唐加福.蚁群最优化-模型算法及应用综述［J］.系统工程学报，2004，19（5）：496-502.LIU Shixin，SONG Jianhai，TANG Jiafu.ant colony opti⁃mization-model algorithm and application of a overview［J］.Journal of Systems Engineering，2004，19（5）：496-502.

Application and Research of MMTD Algorithm in Ant Colony Algorithm

ZHU Lizhi
（Information Center，Nanjing University of Aeronautics&Amp，Astronautics，Nanjing 210016）

Nowadays，computer experts and engineers in order to improve the intelligence of the machine，so in the field of subjects developed many intelligent algorithm.The algorithm is mainly used for the optimal solution to solve the problem.Ant colony algorithm is a kind of intelligent algorithm，which uses the optimal solution of the individual to guide the overall optimal solution.In ant colony algorithm，when the ants find the shortest path，it is important to find the optimal solution with different intensity of pher⁃omone concentration and volatile coefficient.Based on the existing ant colony algorithm，this paper proposes the use of MMTD algo⁃rithm to measure and calculate the evaporation coefficient of ant pheromone，and the application of MMTD algorithm in ant colony algorithm is the main innovation of this paper.

ant colony algorithm，MMTD，pheromone，volatile coefficient，intelligence

Class Number TP301

TP301

10.3969/j.issn.1672-9722.2017.12.006

2017年6月6日，

2017年7月27日

朱俚治，男，工程师，研究方向：网络安全，计算机算法和技术。