基于离散余弦变换和置乱融合模型的图像信息隐藏方法研究∗

陈 胜 王兴众

1 引言

随着信息社会的到来，在信息传输中图像所占的比例越来越大，传统的加密手段由于存在诸多限制，致使某些场景不能得到很好的应用［1］。信息隐藏技术主要是利用载体中的冗余信息，将所要传递的秘密信息嵌入到载体中，使其不易被发现，从而达到秘密通信的目的。在实际应用中，我们可以先对信息进行加密处理，再将加密后的信息隐藏到载体中，从而保证通信的安全性［2］。

信息隐藏在多个领域受到广泛的关注，在现代的各种指挥系统和通信系统中，很多地方用到信息隐藏技术，由于图像的信息量较大，选其作为载体可以得到更大的嵌入量［3］。本文介绍了一种以图像为载体，基于离散余弦变换处理、Arnold置乱和图像融合相结合方法，用于图像的信息隐藏。通过选取礁石和岛屿图像作为载体，多种常见水面目标作为待隐藏图像信息，在Matlab2014环境下进行仿真实验，验证了该方法的有效性。

2 算法模型与框架

2.1 信息隐藏

信息隐藏技术主要包括空域隐藏算法和变换域隐藏算法两大类。空域隐藏算法是在图像的空间域进行信息的嵌入，主要方法是通过对图像的像素值直接进行修改，从而达到隐藏秘密信息的目的［4］。

具有代表性的空域信息隐藏算法主要包括LSB算法，位平面算法以及基于直方图调整的算法等。最常用的是最低有效位算法，是通过改变原始载体图像的最低位或者最低几位的实现信息的嵌入，因为图像的最低几位所含的信息特别少，改变其内容在视觉上不容易被察觉，能够有效实现对数据的信息隐藏［5］。

变换域信息隐藏算法是通过某种变换将载体图像变换到频域，通常是通过离散余弦变换（DCT）或离散傅里叶变换（DFT），然后通过对其频域系数进行调整来达到嵌入信息的目的［6］。

和空域的信息隐藏算法相比，变换域算法的优点在于所嵌入秘密信息的能量可以比较均匀的分布在所有像素上，隐藏效果更加理想，另外如果只对中频系数进行修改，对于一般的噪声攻击和压缩攻击有着很强的鲁棒性［7］。

2.2 离散余弦变换

离散余弦变换是可分离的变换，其变换核为余弦函数，除了一般的正交特性之外，其变换矩阵的基向量有着近似于Toeplitz矩阵的特征向量，在对图像、语音等信号的处理中，离散余弦变换被认为是一种准最佳变换［8］。

二维DCT变换的变换核为

式中，x，u=0，1，2，…，M-1；y，v=0，1，2，…，N-1。

二维DCT变换的定义如下，设f（x，y）为M×N的数字图像矩阵，则：

式中，x，u=0，1，2，…，M-1；y，v=0，1，2，…，N-1。

二维逆DCT变换的定义为

2.3 置乱融合算法

1）Arnold置乱

置乱技术是信息安全领域一种常用的手段，因为对于信息隐藏来说，首先要注意的是其不可感知性，在保证良好不可感知性的基础上再考虑嵌入量大小和鲁棒性。置乱作为一种将秘密信息进行隐藏之前的预处理手段，能够有效提升其不可感知性［9］。

置乱操作的目的是通过特定的算法将要嵌入的图像变成杂乱无章的图像，所采用的置乱算法要满足两个基本条件，一是这种置乱变换是到其自身的一一映射，二是这种变换是到自身的满映射，即变换是可逆的。在经过置乱操作之后，图像看起来像随机分布的白噪声，无法从中提取任何有效的信息，从而将其嵌入到载体图像时，不会引起色彩和纹理的太大变化，提升嵌入后图像的视觉效果【10】。同时，置乱的过程相当于对图像进行加密，不知道所用置乱方法和密钥的拦截者对获取的信息解密需要耗费极大的计算量，因此，在提高不可感知性的同时能有效提高传输的安全性。

可以用于信息隐藏的置乱方法有很多种，其中比较常用的有仿射置乱，Hash置乱，幻方置乱，Arnold置乱等。由于Arnold置乱具有良好的周期性，在置乱矩阵选定之后，对于不同大小的图像，其置乱周期也随之确定。假设待处理的图像大小为M×M，其置乱周期如表1所示。

二维Arnold置乱所用的表达式为

在上式中，x，y是原图像的像素坐标，x′，y′是变换后的像素坐标，保证 | ad-bc|=1。在进行置乱处理的过程中，可将参数a，b，c，d以及置乱次数n作为密钥key，在提取信息并解密时，根据不同的置乱周期和密钥提取信息［11］。

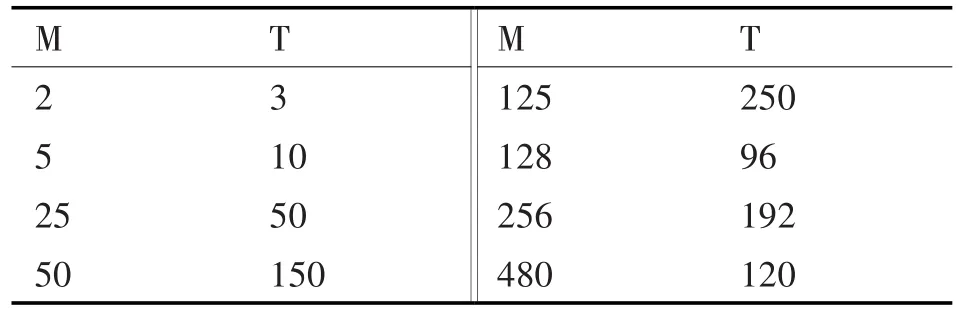
表1 不同大小图像的二维Arnold置乱周期

2）置乱融合算法结构

置乱融合算法包括秘密信息的嵌入和提取两部分，嵌入前首先将待嵌入秘密信息进行Arnold置乱，得到图像并进行分块DCT变换，将之与载体图像进行分块DCT变换后的系数进行融合，融合所用的公式为 S′=Round[aM′+(1-a)N′]，融合后信息进行逆DCT变换即可得到载密图像，其流程如图1所示。

秘密信息的提取流程如图2所示，对秘密信息的提取过程为分别将载密图像和载体图像进行分块DCT变换，将得到的系数按照公式N′=Round[(S′-aM′)/(1-a)]进行提取，得到恢复后的系数并对其进行逆DCT变换并且参考置乱加密时所使用密钥进行处理后解密即可得到所嵌入的信息。

2.4 算法评价指标

信息隐藏算法的基本评价指标包括不可感知性，信息提取质量和鲁棒性等几个方面【12】。其中不可感知性和提取质量均可以用均方根误差（RMSE）和峰值信噪比（PSNR）进行客观评价，鲁棒性是指通信过程中对一些如椒盐噪声、任意涂画或者JPEG压缩等常见攻击的抵抗能力［13］。

1）均方根误差

均方根误差又叫做标准误差，它是观测值与真值偏差的平方和观测次数n比值的平方根，其定义为

其中，式中的g（x，y）和f（x，y）分别代表待比较的两幅图像，如果评价不可感知性，g（x，y）和f（x，y）表示载体图像和载密图像，而如果评价图像的恢复质量，则g（x，y）和f（x，y）表示原始嵌入图像和恢复后的图像，M和N分别表示图像的长和宽。均方根误差越小，表示两幅图像的相似度越高［14］。

2）峰值信噪比

峰值信噪比是一种最常见的评价图像质量的客观标准，其值为原图像和处理后图像之间的均方误差相对于(2n-1)^2的对数值，单位是dB，计算公式为

结合式（5），可以得出：

PSNR越大，表示图像的保真度越好，用在信息隐藏的评价中，即不可感知性更好或者图像提取质量更高［15］。

3 实验设计与结果分析

为了验证算法的有效性，本文选取了几种常见的水面目标，包括海警船、油船、两栖攻击舰、驱逐舰、航空母舰、豪华游艇、渔船、散货船和潜艇9种目标的图像作为待传输的信息，以礁石和岛屿两种图像作为载体图像进行实验。

3.1 算法实现步骤

置乱融合算法的实现主要包括信息的嵌入和提取两个部分，为了方便处理，本文所采用的嵌入信息和载体均为512×512的灰度图像，具体的实验设计步骤如下。

1）秘密信息嵌入过程

（1）将大小为512×512的载体图像和待嵌入图像分别记为M和N；

（2）对N用Arnold置乱变换进行加密处理，得到置乱后的图像并记为P，并将所用到的置乱矩阵参数a，b，c，d和置乱次数n作为密钥key保存；

（3）将M和P分成大小为8×8的块，对每个块分别进行DCT变换，得到其DCT系数矩阵，分别记为M′和P′；

（4）根据融合公式 S′=Round[aM′+(1-a)P′]对M′和P′的DCT系数进行融合，式中的a为融合系数，且满足0＜a＜1，Round为向上取整的操作，S′为融合后的DCT系数，对其进行分块IDCT变换就可以得到嵌入后的载密图像S。通过改变融合系数a的值，可以得到不同的融合结果。由融合公式就可以看出，当系数a越接近1时，所得到的结果S越接近原始载体图像M，但所嵌入的信息量越少，因此，通过选择合适的系数，可以将待嵌入信息较好地隐藏于载体中。

2）秘密信息提取过程

（1）对接收到的载密信息图像S和原始载体图像M分别进行分块DCT变换，得到其DCT系数矩阵S′和M′；

（2）利用提取公式 P′=Round[(S′-aM′)/(1-a)]，取嵌入时的融合系数代入，对其进行IDCT变换可以得到嵌入的秘密信息P；

（3）根据密钥key对P进行解密操作，即可得到原始要嵌入的秘密信息N。

3.2 实验结果与分析

实验得到海警船、油船、两栖攻击舰、驱逐舰、航空母舰、豪华游艇、渔船、散货船和潜艇9种目标在礁石和岛屿两种图像载体下的信息嵌入和提取结果，图3和图4分别给出了海警船和两栖攻击舰的实验结果，图中从（a）到（f）分别是待嵌入图像，载体图像，待嵌入图像经过置乱加密后的结果，嵌入后的载密图像，提取的信息和经过解密得到的嵌入信息。

从图中可以看出，置乱加密后的待嵌入信息近似白噪声，且嵌入后的载密图像在肉眼上无法看出和载体图像区别，信道中传输的是载密图像d，图像（e）为提取的嵌入信息，即使被人截获并提取，当不知道加密所用的key时，也无法获取到有用信息。表2给出了9种实验图像嵌入礁石和岛屿两种不同载体图像中时载密图像的均方根误差和峰值信噪比，表3给出了提取图像均方根误差和峰值信噪比。可以看出，通过选取合适的置乱次数和融合系数，基本上可以使载密图像和提取图像的峰值信噪比均达到34dB以上，从而保证具有良好的不可见性和提取质量，达到信息隐藏和有效传输的目的。

与文献［16］中采用的直接融合的方法进行比较，结果在表4中给出，可以看出经过置乱加密再进行频域系数融合，除了保证更高的安全性之外，得到的嵌入质量也有一定的提高，即嵌入的不可感知性更好，信息的提取质量和直接融合的方法差距不大。

4 结语

文章在传统的信息融合思路的基础上，结合DCT变换并且先将待嵌入信息进行置乱加密，使得信息隐藏的不可感知性得到一定提高，并且增加了传输过程的安全性，通过9种目标图像在2种不同载体中的实验，验证了该方法的有效性。受嵌入的信息量所限，其提取的图像质量与直接融合的方法相比并没有明显的提高，这是下一步改进优化的目标和方向。

表2 载密图像均方根误差和峰值信噪比

表3 提取信息均方根误差和峰值信噪比

表4 与直接融合算法峰值信噪比对比

［1］钮心忻，杨义先，吴志军.信息隐藏理论与关键技术研究.电信科学，2004，12：28-30.

［2］Z.Zhao，H.Luo，Z.M.Lu，and J.S.Pan，Reversible data hiding based on multilevel reversiblehistogram modification and sequential recovery［J］.Int.J.Electron.Commun，2011，65（10）：814-826.

［3］崔忠立，王嘉祯.一种替换类隐写术算法的统一模型［J］.计算机工程与应用，2006，13：127-129

［4］Rafael C.Gonzalez，Richard E.Wood.数字图像处理（第三版）［M］.电子工业出版社，2017：352-354.

［5］沈昌祥，张焕国，冯登国等.信息安全综述［J］.中国科学E辑，2007，37（2）：129-150.

［6］刘志军.基于小波域块分类的的信息隐藏算法［J］.计算机工程，2008，34（12）：144-146.

［7］谢健全，阳春华.大容量的信息隐藏算法［J］.计算机工程，2008，34（8）：167-169.

［8］W.L.Tai，C.M.Yeh，and C.C.Chang.Reversible data hiding based on histogram modification of pixel differences［J］.IEEE Trans.Circuits Syst.Video Technol.，2009，19（6）：906-910.

［9］颚炜，康宝生.基于置乱与融合的数字图象隐藏技术及其应用［J］.计算机应用与软件，2008，5（25）：216-217.

［10］朱桂斌，曹长修，胡中豫等.基于仿射变换的数字图像置乱加密算法［J］.计算机辅助设计与图形学学报，2003，15（06）：711-715.

［11］H.W.Tseng and C.P.Hsieh，Prediction-based reversible data hiding，Informat.Sci.，2009，179（14）：2460-2469.

［12］陈明奇，钮心忻，杨义先.基于小波变换及矢量量化的隐像术［J］.计算机研究与发展，2001，38（2）：199-203.［13］陈铭，平西建.基于Arnold变换的图像信息伪装算法［J］.计算机应用研究，2006，01：235-238.

［14］H.C.Huang and W.C.Fang.Authenticity preservation with histogram based reversible data hiding and quadtree concepts［J］.Sensors，2011，11（10）：9717-9731.

［15］C.Y.Yang，C.H.Lin，and W.C.Hu.Reversible data hiding by adaptive IWT-coefficient adjustment［J］.J.Informat.Hiding Multimedia Signal Process.，2011，2（1）：24-32.

［16］张贵仓，王让定，章毓晋.基于迭代混合的数字图像隐藏技术［J］.计算机学报，2003，26（5）：569-574.