带时间窗的航母编队多补给船海上补给路径规划∗

王城超 邹 强 贾汝娜

1 引言

海上补给路径规划是一个NP-Hard难题，是海上补给规划的研究重点。在航母编队海上补给过程中，由于编队内作战舰艇数量较多，各作战舰艇所处的位置相对分散且距离较远，作战时各舰艇的位置可根据作战需要而变动，补给策略多样，这些都使得航母编队海上补给路径规划问题趋于复杂化［1］。目前，国外对海上补给路径进行了大量研究，将其视标准TSP问题、广义TSP问题或广义定向问题［2～6］，Williams［7］将海上补给路径规划将其视为车间调度问题（VRP）。国内对航母编队海上补给路径规划研究较晚，主要是针对编队单补给船海上补给路径规划［8～10］方面的相关研究，大多是将TSP问题的基本思想进行适当改进，应用到单补给船海上补给路径规划中去。针对编队多补给船海上补给路径规划，国内难以查到研究该问题的文献。从航母编队的发展趋势来看，航母编队单补给船海上补给路径规划难以满足航母编队的海上补给保障需求。航母编队补给船补给模式主要有三种，即送报男孩（delivery boy）模式，加油站（gas station）模式，巡回牧师（circuit rider）模式，考虑到本文篇幅有限，故本文只研究送报男孩模式下的航母编队多补给船海上补给路径规划。基于此，本文研究送报男孩模式下带有时间窗的航母编队多补给船海上补给路径规划（Undeyway Replenishment Routing Scheduling Problem with Time Windows，URRSPTW），可为航母编队伴随补给保障提供策略支持。

2 VRPTW问题与URRSPTW问题的联系与区别

URRSPTW问题与VRPTW问题之间既存在相同之处，也存在部分区别。因此在对URRSPTW问题进行描述与求解时，一方面，要充分吸取VRPTW问题中可以运用的成功经验；另一方面，要充分考虑URRSPTW问题的独特属性。此外，URRSPTW问题是基于编队作战条件下的补给路径规划问题，所以求解URRSPTW问题的考虑的因素和求解过程的复杂性更高。所以URRSPTW问题的求解思路是在URRSPTW问题与VRPTW问题共性的基础上，结合URRSPTW问题作战等独特因素的影响来求解该问题。

两者的相同之处：URRSPTW问题与VRPTW问题都属于复杂化的优化问题；都是采用图论中顶点和赋权的边方法对其进行描述；图中每个定点都只能被访问一次。

两者的不同之处：1）图方面，对于VRPTW问题，其图论中描述的顶点表示固定的被服务点，而对于URRSPTW问题来说，其图论中描述的顶点是作战舰艇补给时所处的位置。2）目标函数的选择方面，VRPTW模型的目标函数一般为单目标（补给总时间、补给总距离或补给总成本等最小），而URRSPTW问题的目标函数与作战等因素密切相关，一般为多重目标（如补给船选择数量尽量少、最小化编队补给总时间、因补给而生成的编队作战效能最大等），根据作战实际情况，目标函数可选择其中的一个或多个。3）配送车辆或伴随补给船数量限制方面，VRPTW问题的配送车辆数量一般未进行限制，最大限度地满足客户的配送需求，但在优化目标中设置配送车辆数量尽可能少；而URRSPTW问题伴随补给船的数量一般受到严格的限制，在极短情况下（比如同一段时间出现较多作战舰艇的补给需求），很可能会出现伴随补给船不能满足全部作战舰艇的补给时间窗要求的情况，此时优先选择因补给而生成作战效能最大的作战舰艇进行补给。4）时间窗方面，VRPTW问题时间窗是客户给定的，URRSPTW问题的时间窗是通过预测得到的。

3 URRSPTW问题的数学描述

3.1 补给模式描述

假设航母编队作战时，补给船位于航母编队的内部，并时刻受航母编队的保护。在该补给模式下，编队内作战舰艇位置不变，根据编队内各作战舰艇的弹药补给需求，若干艘补给船离开其初始位置，以一定的顺序对各作战舰艇进行弹药补给。由于在补给船补给过程中，编队内作战舰艇在原有位置，最大程度地保证了编队阵形的完整性，此情况对航母编队作战最为有益，但是该补给模式也存在一定的缺陷，比如补给船不能同时对两艘作战舰艇进行弹药补给。下面以10艘待补作战舰艇和2艘补给船为例，该补给模式下的补给路径规划示意图如下。

3.2 模型假设条件

在航母编队实际作战中，URRSPTW问题涉及的因素较多，在建立数学模型对其进行求解时，建立的数学模型肯定与真实情况下的URRSPTW问题有部分差异。所以为了能够准确地对URRSPTW问题进行建模，必须根据实际情况对模型做出一定的假设，基本假设如下：

1）航母编队有k艘伴随补给船对编队中作战舰艇进行弹药伴随补给，k艘伴随补给船没有航行距离限制；

2）补给船从初始位置出发，依次对各待补作战舰艇进行补给，补给结束后补给船回到初始位置，该段时间被称为编队补给时间；

3）每艘补给船的弹药储备量Q可满足编队作战舰艇的所有补给需求；

4）伴随补给船可在战斗中随时对编队内待补作战舰艇进行弹药补给；

5）每艘作战舰艇只补给一次；

6）每艘待补作战舰艇的补给时间窗已知，可表示为[ ]ETi，LTi。只要补给船对该作战舰艇的开始补给时间在时间窗[ETi，LTi]内，即称补给满足时间窗约束。

3.3 符号定义

本文用图论的方法来描述编队多补给船补给路径规划问题。定义无向图G=(V ，A) ，点集V={0 ，1，…，n} ，其中{0}表示补给船的初始位置，V{0}表示待补作战舰艇的位置集合；弧线集合A={( i ， j)|i，j∈V，i≠j} 表示连接2个待补作战舰艇之间的航行路线的集合，当i或j的值为0时，表示处于补给船的初始位置。

数学模型中的参数含义及决策变量如下：n表示航母编队中待补作战舰艇的数量；k表示补给船索引变量，k∈K={1 ，2，…，M } ；ri表示伴随补给船对待补作战舰艇i的补给作业时间；tsi和tei分别表示伴随补给船对待补作战舰艇i补给开始前的准备和撤离时间；dij表示伴随补给船从作战舰艇i航行至作战舰艇j（包括补给船初始位置）的时间；Tia表示补给船到达作战舰艇i的时间；Tis补给船对作战舰艇i的开始补给时间；Tja补给船到达作战舰艇j的时间；补作战舰艇i补给的时间窗为［ETi，LTi］。

3.4 模型建立

在满足流程约束、时间窗约束和整数性与非负性约束等条件下，建立以完成编队作战舰艇弹药补给的最小化补给船数量和最小化补给航行时间为目标的数学模型。

目标函数：

流程约束条件

时间窗约束条件：

式（1）为目标函数，其中 p1、p2为整数，且有p1≫p2。目标函数是一种组合化的目标函数，第一目标为最小化补给船的使用数量，第二目标为编队最小化补给航行时间。

式（2）～（6）为流程约束条件，保证了补给船从初始位置出发，补给结束后回到初始位置。式（2）～（3）表示每艘作战舰艇仅由一艘补给船补给弹药，且确保了每艘作战舰艇都能被一艘补给船补给一次。式（4）是为了确保线路的连续性，且输入输出弧相等。式（5）～（6）是为了确保补给船从初始位置出发，并保证补给结束后返回初始位置。

式（7）～（8）为时间窗约束条件。式（7）表示补给船到达作战舰艇的时间约束，保证了补给时间的连续性。式（8）表示补给时间窗约束，补给船对待补作战舰艇i的最早开始补给时间满足作战舰艇i的补给时间窗[ETi，LTi。]

4 改进GA的设计

GA最早是由美国J.Holland教授提出的，是一种模拟生物界中遗传和进化的算法［11～12］。GA具有较强的全局搜索能力，同时解的表示方法也很直观清楚，但是也存在容易陷入局部最优等缺点，所以本文采用改进GA来求解URRSPTW问题。改进GA的基本流程如下图。

下面对改进GA的设计步骤进行详细阐述。

1）染色体结构设计

设计染色体结构包括染色体编码方式和编码长度的确定。

本文采用的染色体编码方式是较为直观的自然数编码，该方法的优点是占用计算机内存较小，同时解的表示方法直观清楚。假设待补作战舰艇的数量为m，补给船数量为k，该编码方法首先是随机生成一种由0和1～m之间不重复自然数组成排列的补给方案，该排列就代表了问题的一个解。假设“0”表示补给船的初始位置，“1，2，…，m ”表示m艘作战舰艇的补给需求点集合。以染色体“0421078906530”为例，该染色体表示补给船补给路径规划方案，即表示3艘补给船从原始位置出发，对9艘作战舰艇补给需求点进行补给作业。补给路径规划方案具体如下：

第一艘补给船补给路径：补给船初始位置→需求点4→需求点2→需求点1→补给船初始位置。

第二艘补给船补给路径：补给船初始位置→需求点7→需求点8→需求点9→补给船初始位置。

第三艘补给船补给路径：补给船初始位置→需求点6→需求点5→需求点3→补给船初始位置。

染色体长度=补给船总数+需求点数+1。

2）适应度函数

在遗传算法中，通过适应度大小来区分种群中个体的优劣，故设计合理的适应度函数尤其重要。一般可根据模型中目标函数设计相应的适应度函数，假设 f(x)表示目标函数，F(x)表示适应度函数，则将 f(x)转化为F(x)的过程定义为标定［13］（Scaling）。本文采用的标定方式是动态线性标定，具体如下：

其中k表示待定参数，且k的取值一般较大；x表示种群中的某个个体，f()x表示种群个体x的目标函数；通过对目标函数进行上述标定，得到的适应度函数F()

x能够较好地均衡GA的全局搜索与局部搜索。

对于目标函数 f()x有必要做进一步阐述。由于GA在求解编队补给船路径规划时不能直接处理模型中的约束条件，故必须把相关约束条件做进一步转化，并转移到目标函数中去。

考虑到URRSPTW模型中时间窗约束的重要性，基于GA的原理，设计的目标函数 f()x具体如下

其中Tis表示补给船对作战舰艇i的补给开始时间。目标函数 f(x) 中 p1、p2、A、B均为常数，目标函数f(x)是一种组合化的目标，常数 p1、p2、A、B的取值直接关系到GA中适应度值的准确度。目标函数f(x)中包括三重组合化目标，第一目标为时间窗约束目标，第二目标为最小化补给船的使用数量，第三目标为编队最小化补给航行时间，所以常数 p1、p2、A、B的取值应满足以下条件：

例如 p1、p2、A、B的取值可以为 A=1000，B=1000，p1=100，p2=10。

3）选择操作

本文采用的选择策略是Proportional Selection，假设种群数量为n，种群中个体i被选择的概率计算公式如下：

其中Pi表示个体i被选中的概率；Fi表示种群中个体 i的适应度值表示种群中所有个体的适应度值总和。

在Pi确定之后，本文采用的选择操作方法是Roulette Wheel（轮盘赌法）。记 PP0=0，假设有个圆形轮盘，根据PPi(i =1，2，…，n)将整个轮盘分为n份，则圆形轮盘中第i个扇形的角度数为2πPPi。随机生成一个随机数r∈U(0 ，1) ，若 PPi-1≤r＜PPi时，则选择个体i，该选择操作中共生成n个随机数。很显然，Pi较大的个体i的在圆形轮盘中占用的面积较大，该个体被选择的概率也较大，被遗传到下一代的概率也越大。

因目前不少高校开设了国外合作办学专业，可采取国内高校-国外高校-企业三方合作模式，共同订制人才培养方案，并与企业需求相对接，同时完成教学、实践任务。在国外、国内都给学生提供企业实习机会，丰富学生职业实践经历，提高意识，帮助他们不断修正和评估自我，完善职业规划。

4）遗传算子的设计

（1）交叉算子设计

本文中交叉算子的设计可以避免GA陷入局部最优。交叉操作可分两步进行，第一步是将上述选择操作中选出的染色体进行两两配对，然后再根据交叉率来决定该对染色体是否进行交叉操作；第二步是设置配对染色体中的交叉点，并进行交叉互换。

OX是在传统PartiallyMatched Crossover（PMX）的基础上改进得到的，在求解URRSPTW模型中有较大的优势。OX的步骤如图3所示。

OX运算示意图如下。

本文采用顺序交叉法（简称OX）和改进OX来对染色体中基因进行交叉互换。若被选出待交叉的两个个体不同，则采用上述OX进行交叉操作；若被选出待交叉的两个个体染色体完全一样，则采用改进OX进行交叉操作（即将这两个个体中一个个体被选中将进行交叉的基因移入该染色体的首位，而将另一个体将进行交叉的基因移到该染色体的末尾）。

变异算子的实质是对补给船的补给路径规划线路中的部分可行解进行局部寻优。设置变异算子的作用是加速GA的收敛速度和避免早熟现象发生。变异操作包括两个步骤：首先依据变异率来决定是否进行变异操作；如果确定进行变异操作，则通过特定的变异操作方法来完全变异操作。

本文采用的变异操作方法是交换变异法（亦可称为对称变异法），该方法是指随机选择基因片段中排列的两艘作战舰艇，交换两者的位置。例如个体“87654321”，假设随机交换第2位和第7位，则有87654321→82654371。

（3）终止条件

本文将改进GA的终止条件设置为最大进化代数M。

5 实例分析

本文以一种典型双航母编队的海上补给路径规划为例，编队构成包括2艘航母母舰、3艘伴随补给船、15艘编队附属水面舰艇，对所提出的的模型与方法进行验证。

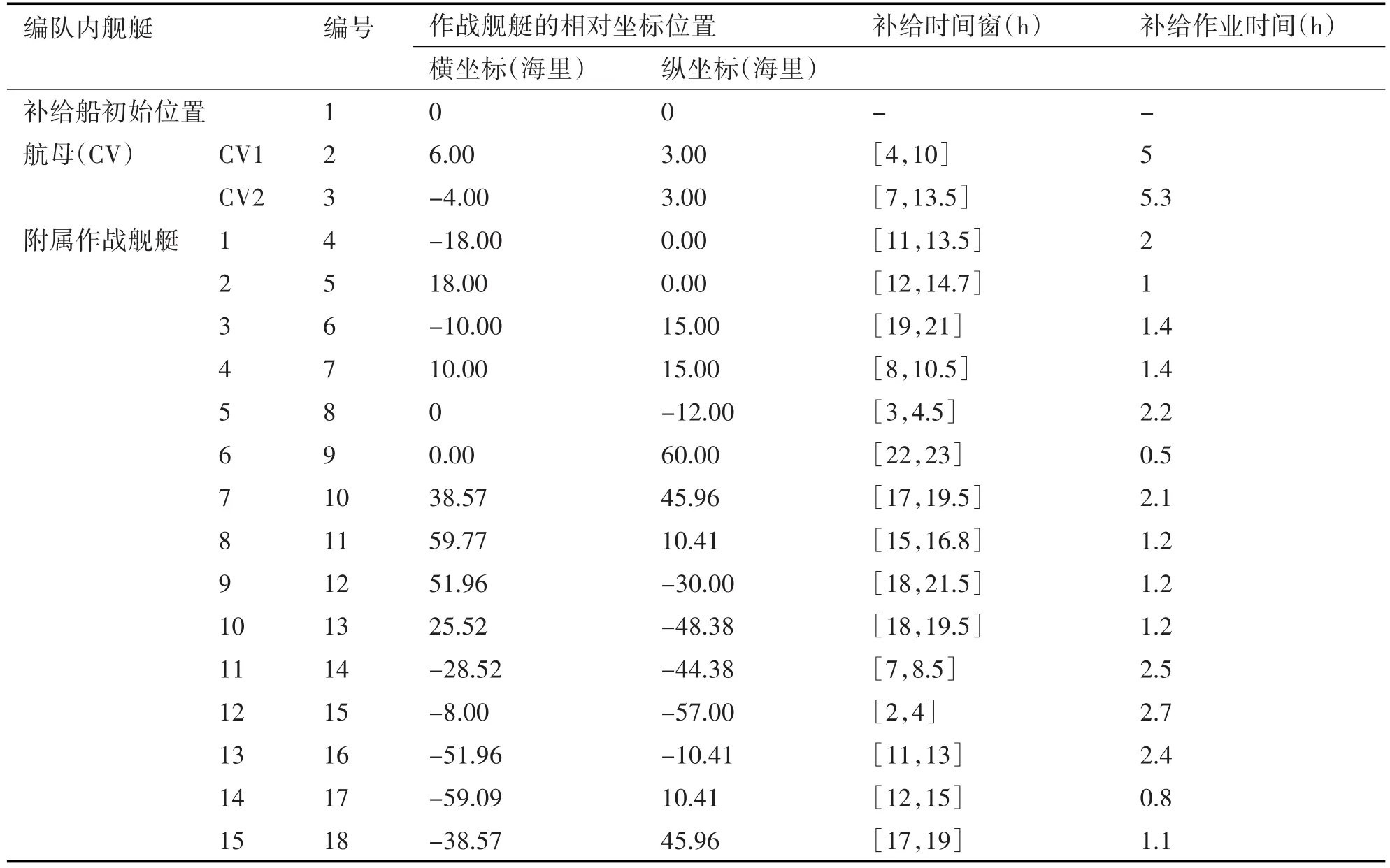
表1 输入初始数据

5.1 初始输入数据和相关参数设置

1）初始输入数据

假设3艘伴随补给船的初始位置都处于坐标中心，编队中伴随补给船的初始位置编号1，各作战舰艇补给需求点位置依次编号2、3、…、17。由于保密原因，本文的初始输入位置等是人为给定的，具体如下。

2）相关参数设置

（1）补给船的平均航速v=25节（海里/小时）；

（2）改进GA的相关参数设置为：种群大小n=60，最大迭代次数M=200，交叉率 Pc=0.9，变异率Pm=0.1；

5.2 航母编队多补给船补给路径规划结果

采用改进GA对航母编队多补给船海上补给路径进行10次实例仿真，选取仿真结果中的一个较好结果，其最优航母编队多补给船海上补给路径规划方案如表2。

表2中的航母编队多补给船海上补给路径规划方案由三艘补给船的补给路径组成，其中1号补给船在t=0h时刻就从该补给船的初始位置出发，并开始补给作业，该补给船完成该补给船所在路径上全部补给任务所花的时间是22h；2号补给船在t=2.5h时刻从该补给船的初始位置出发，并开始补给作业，该补给船完成该补给船所在路径上全部补给任务所花的时间是24.1h；3号补给船在t=3.7h时刻从该补给船的初始位置出发，并开始补给作业，该补给船完成该补给船所在路径上全部补给任务所花的时间是24.9h。编队补给总时间表示编队内伴随补给船完成航母编队多补给船海上补给路径规划中全部作战舰艇的补给作业所花费的时间，即为3条路径补给时间中的最长者（24.9h）。

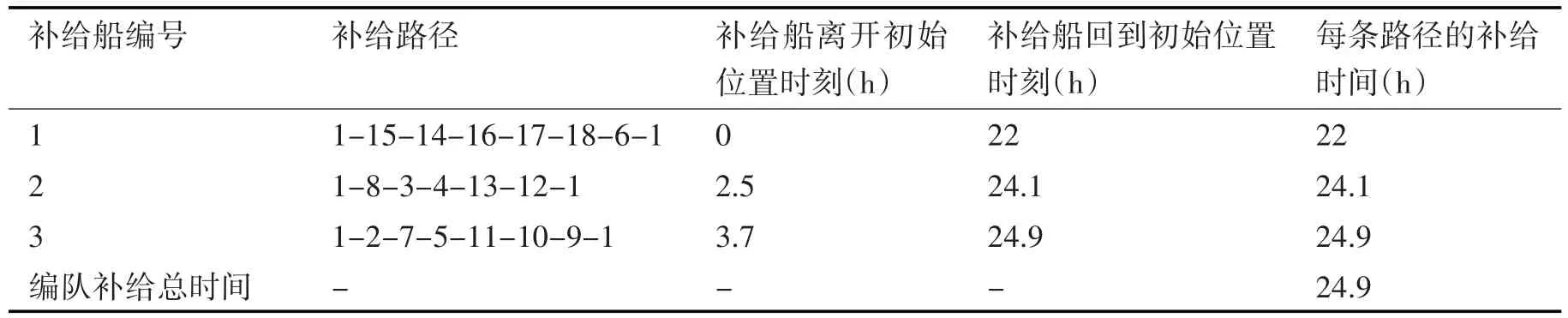
表2 航母编队多补给补给路径规划方案

在该航母编队多补给船海上补给路径规划方案下，航母编队多补给船海上补给路径规划图如下所示。

航母编队多补给船海上补给路径规划图由三艘补给船的补给路径组成，为了图中补给路径清晰可见，分别采用不同的线条对三艘补给船的补给路径进行了标记。

在该航母编队多补给船海上补给路径规划方案下，补给船对各作战舰艇进行补给作业的实际到达时刻、等待时间、开始补给时刻和补给结束后的实际离开时刻等时间情况如表3所示。

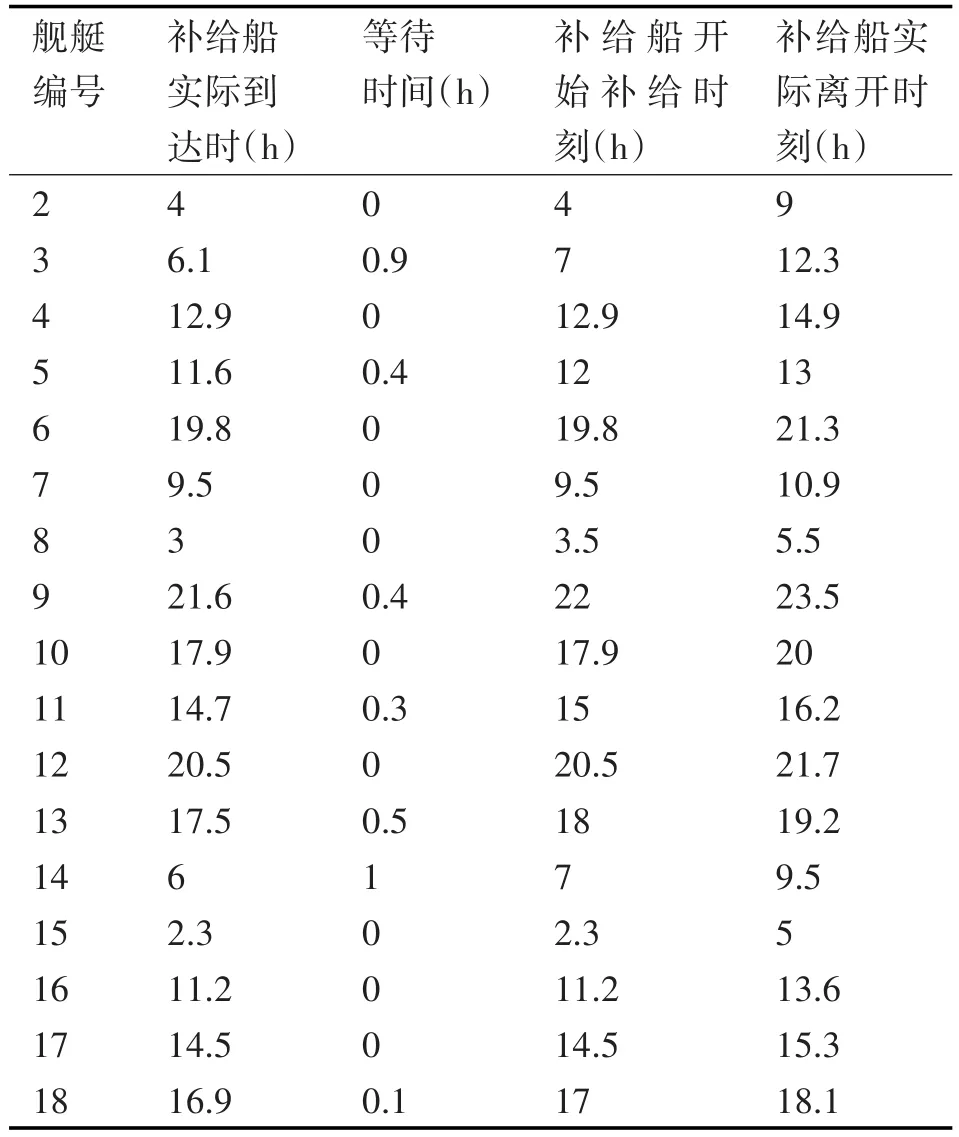
表3 航母编队多补给船海上补给路径规划的相关时间情况表

6 结语

本文研究带时间窗的航母编队多补给船海上补给路径规划问题。首先将URRSPTW问题和VRPTW问题进行了对比，分析了两者的区别与联系。在此基础上，建立了URRSPTW问题的数学模型，并提出了改进GA来求解模型，该方法能够避免陷入局部最优。最后选取了一种典型航母编队多补给船海上补给路径为案例，进行了实例分析，得到了多补给船补给路径规划方案和补给路径规划图，计算结果验证了该模型与方法的合理性，可为航母编队伴随补给保障提供策略支持。

［1］Conley T E.Analysis of pacific fleet underway replenishment data［D］.Montery：Naval Postgraduate School，1988：14-25.

［2］Dunn J S.Scheduling underway replenishment as a generalized orienteering problem［D］.California：Naval Postgraduate School，1992：25-40.

［3］Wu，Tzu-Li.Optimization Models for Underway Replenishment of A Dispersed carrier Battle Group［D］.California：Naval Postgraduate School，1992：1-15.

［4］Hardgrave S W.Determining the feasibility of replenishment a dispersed carrier battle group［D］.California：Naval Postgraduate School，1989：6-21.

［5］Zabarouskas M W.Scheduling underway replenishment using delivery boy and circuit rider tactics，an asymmetric generalized TSP［D］. California：NavalPostgraduate School，1992：10-29.

［6］DeGrange W C.Optimizing global combat logistics force support for sea base operations［D］.California：Naval Postgraduate School，2005：3-15.

［7］Williams T M.Heuristic scheduling of ship replenishment at sea［J］.Journal of the Operational Research，1992，（43）：11-18，5-21.

［8］余鹏，何学军.基于蚁群算法的舰艇编队海上补给路径规划方法［J］.海军工程大学学报，2014，26（2）：108-112.

［9］周晓光，赵厚仁，王述运，等.航母编队补给船海上补给航路规划［J］.系统工程与电子技术，2014，36（9）：1756-1760.

［10］黄必佳，王公宝.航母编队油料伴随补给规划模型及算法研究［J］.兵工自动化，2015，34（9）：78-83.

［11］韩庆田，曹文静，苏涛.基于遗传算法的舰载机保障流程研究［J］. 科学技术与工程，2012，12（35）：9784-9787.

［12］史峰，王辉，郁磊，等.Matlab智能算法30个案例分析［M］.2版.北京：北京航空航天大学出版社，2015：108-117.

［13］汪定伟，王俊伟等.智能优化方法［M］.北京：高等教育出版社，2007：63-64.