拉索振动的参数分析及测试系统研究

傅理文，吴书正，夏庆云

（1.浙江广川工程咨询有限公司，浙江 杭州 310020;2.浦江县河道管理站，浙江 浦江 322200）

拉索振动的参数分析及测试系统研究

傅理文1，吴书正2，夏庆云1

（1.浙江广川工程咨询有限公司，浙江 杭州 310020;2.浦江县河道管理站，浙江 浦江 322200）

针对大跨桥梁健康监测的测试精度问题，基于实际工程中不同类型拉索的动力特性进行参数分析，采用数值计算作为不同类型拉索测试的动力分析方法，采用LabVIEW作为开发平台，配合NI（美国国家仪器公司）相应的数据采集模块，构建一套可应用于现场快速完整测试的测试系统。系统内容主要包含数据信号处理（采样信息、滤波设置、测试构件所需参数）、数据信号(时域、频域、索力)显示及存储、频率索力关系修正，经数值拉索模型验证，完全满足工程测试精度要求。

拉索结构;振动特性;健康监测;索力测试系统

0 引言

拉索作为大跨桥梁工程中一种质量轻、阻尼小、柔度大的承重构件，极易在风、雨、车辆、支座激励等外界因素作用下产生不同机理的振动[1]。拉索振动会引起结构疲劳，造成防护层及锚固端的破坏，从而诱发拉索锈蚀乃至失效，易危及结构安全，影响桥梁正常使用性能的发挥。一般而言，拉索造价占全桥造价的25%～30%；抑制拉索振动的费用也高达全桥造价的2%～10%；若更换拉索，其所造成的运营中断将进一步扩大损失[1,2]。因而，作为常年暴露于大气中的构件，有必要对拉索进行定期的索力测试以评估服役期及拉索乃至整体结构的健康状况。目前，基于频率法的索力测试仍是桥梁运营阶段较为广泛使用的方法，其技术、理论相对成熟，但就实际工程中仍存在效率不高、精度不足的问题。因而，编制一套参数可配置而计算高效、界面友好的索力测试系统对工程测试与分析具有实际意义，其开发主要包含索动力特性的研究和测试程序的编制实现。

1 拉索动力分析方法

拉索的动力研究由来已久：最初古希腊的Pythashed从风弦琴奏出的乐声中察觉到音调与弦张力、长度、质量间存在一定的关系。较为严谨的振动理论初步形成于18世纪上半叶，由Taylor及其之后的 d’Alembert、Euler、Bernoulli逐步建立发展。上世纪70～80年代，H.M.Irvine,Caughey建立线性小垂度索的经典力学理论，对索动力问题进行了详尽而系统的研究[1]。索动力研究包含解析法、有限元法以及实验法：解析法一般用来分析结构相对简单的纯索，其有助于理解拉索相关参数的物理含义；数值解法则可较好地模拟实际索构件的空间位置、尺寸、材料特性、连接形式、初始应力和初始变形等，根据结构仿真分析的初始形态可得到相对详尽、精确和可靠的分析结果。

1.1 索动力分析解析法

常用的索结构自由振动基本方程主要包含两类，一类是轴向受拉梁模型，一类是小垂度弹性索模型：前者动力方程不考虑索的垂度影响，后者动力方程则不考虑索的刚度影响。两者都包含几个基本假定:（1）只考虑拉索竖直平面的振动;（2）不考虑拉索的阻尼影响;（3）认为拉索材质均匀，材料的应力应变关系符合胡克定律，且变形前后拉索截面积保持不变。此外，基于前梁振动模型可进一步推导得到不考虑抗弯刚度的弦振动模型以及边界条件考虑减震器影响的梁振动模型。

（1）轴向受拉梁振动模型频率方程

铰支约束：

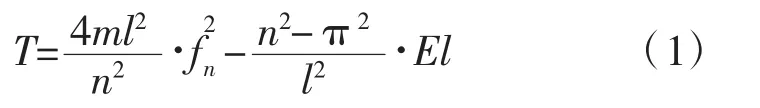
固端约束：

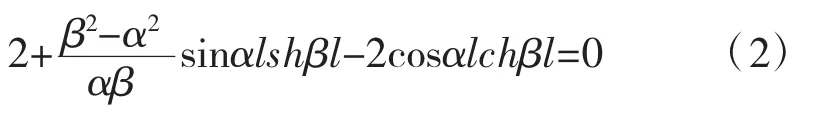
式中：m为索的单位长度质量；T为索所受的张力；EI为索的抗弯刚度；l为索的长度；fn为索的n阶频率；ω为索振动的圆频率。在铰支约束下，索力是其频率的显式关系式；在固端约束下，索力值需迭代求解。

（2）小垂度索振动模型频率方程

铰支约束：

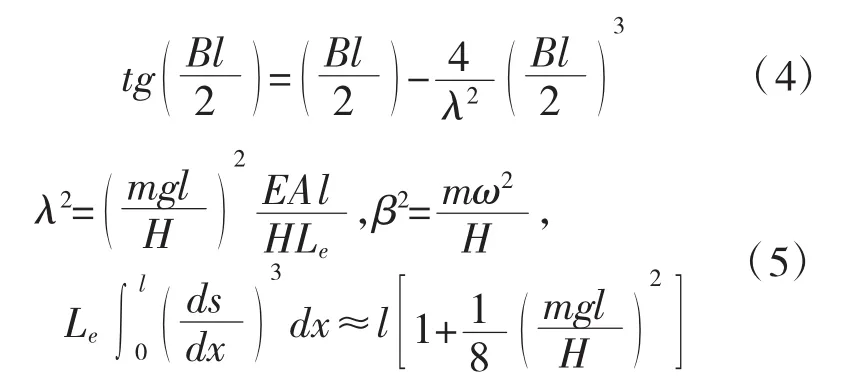
式中：m为索的单位长度质量；H为索张力的水平分量；EA为索的抗拉刚度；l为索端点间的水平长度；Le为拉索的曲线长度；ω为索振动的圆频率。该超越方程关于λ2表现出强烈的非线性。λ2括号内的第一项反映索的几何形状，括号外一项反映索的弹性性能。

1.2 索动力分析有限元法

对于具有内张力拉索的刚度，除了包含与其材料特性相关的弹性刚度K之外，还包含与拉索初始应力相关的几何刚度矩阵Kσ。因此，有初始应力的无阻尼结构线性动力学分析可由以下方程表示：

动态响应：

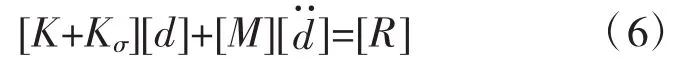
固有频率：

2 拉索振动特性参数分析

解析模型中唯有梁振动模型中铰支边界条件下的频率方程为显式表达，其余均需迭代求解。针对工程中不同特征的索构件，基于假定所得的单一索力计算公式难以满足不同实测对象的适用需要，不同边界及力学特性条件下的索构件测试精度影响不一。有限元法可较好地克服解析法适用条件单一及复杂工况下求解效率低的不足，故下文采用数值模拟对特定参数索构件进行动力特性研究。

建立单索数值模型，分别就其刚度、长度和边界条件进行比较分析。拉索按不同的分析参数建模，其固定参数主要包含：弹性模量1.9×1011Pa；线分布质量48 kg/m；截面积0.006 m2；索拉力在1×106～1×107N区间变化，并以1×106N的倍数取值。

（1）抗弯刚度

实际拉索的抗弯刚度由钢丝弹性模量、钢丝截面面积和截面惯性矩决定。其值介于索中钢丝完全粘结与不完全粘结之间[2]。该处根据不同拉索的惯性量数值变化建立不同抗弯刚度的拉索模型，令索惯性量在0～5.0×10-6m4区间内变化（即抗弯刚度在0～9.5×105N·m2区间变化），并以1.0×10-6m4递增取值计算。

图1不同抗弯刚度拉索动力特性分析图

图1 中，横坐标均为索张拉力，纵坐标f/f′为不同抗弯刚度取值拉索与不计抗弯刚度拉索的频率比值。惯性量的变化在索张拉力较小时，对拉索频率变化影响明显，随着张力的增加，该影响有减小的趋势。该由于固定结构材料参数下的拉索频率值受几何刚度以及弹性刚度影响，当轴力较大时，索力、频率间换算关系主要受几何刚度影响，索惯性量变化所引起弹性刚度变化对频率计算结果影响不大，因而，10 m、100 m拉索在相同惯性量变化下，频率变化渐小。此外两图中，在相同的索力作用下，惯性量对于短索（10 m）频率值的影响较长索（100 m）明显。当惯性量变化为时，在所给索力变化范围内，10 m短索的频率变化量最大达到5.69%，而100 m长索的频率变化量最大约为0.06%，两个变化量的最值都是在索力相对较小时出现，该表明抗弯刚度的准确取值对索力不大的短索动力分析有不可忽略的作用。

（2）边界条件

拉索边界条件的模拟很大程度决定于其锚端形式，主要包含固支、铰支及固支铰支耦合三种情况[2]。该处以铰支约束的索动力分析结果作为基准，根据前文给定参数条件下长、短索模型在不同边界条件下的计算结果进行比较。

图2不同边界条件拉索动力特性分析图

图2 中，横坐标均为索张拉力，纵坐标f/f′为不同边界条件与铰支边界下的拉索频率比值。由图可见，固支条件对10 m短索的动力特性影响较100 m长索更为明显，且索力较小时边界条件对索力结果数值影响较轴力较大时更为明显。上图中，给定参数的10 m短索，其固支边界的最大频率结果较相应条件下铰支边界的最大动力分析结果大约9.57%。

（3）拉索长度

拉索长度常以边界条件的等效换算作为频率结果综合影响参数的组成部分予以统一考虑[4,5]。该处根据前文给定参数，分别建立5 m、20 m、50 m、60 m和80 m铰支边界下的拉索模型。

图3不同长度拉索动力特性分析图

图3 中，横坐标为拉索张拉力，纵坐标f/f′为不同长度拉索与80 m拉索动力分析所得的频率比值。由图3见，5m短索的频率远远高于20 m以上的拉索频率，随着拉索长度的增加，该索力范围内的拉索频率间的差值趋小。因而，索的长短也是影响索动力特性的极大因素。给定材料参数条件下，索长越长，其长度变化所引起的频率变化就越小。

在工程中，短、长索频率变化的影响因素主要受其轴向张拉力、刚度及边界条件的综合影响，犹以短索为甚。针对不同特性的索构件，有限元法可快捷有效地进行索动力分析，该作为一种统一的数据分析模式可运用于测试系统的索力计算中，便于形成相对系统的索动力分析文件（索力-频率对应数据），在工程现场通过测取目标拉索的频率，进行插值运算予以调用分析。

3 拉索振动测试系统开发

基于NI公司的图形化软件LabVIEW，通过功能定义及程序集成实现数据采集、处理、显示及存储的完整过程控制。根据索力测试现场的时效、精度以及实际使用要求，目标设计系统基本指标如下：

（1）实现测试系统的多通道数据采集以节约现场测试效率。

（2）实现用户自行参数操作功能以应对不同测试环境下（车辆荷载、风荷载等影响）的数据采集功能。

（3）实现索力测试分析模式的选择功能，即索力频率间不同的动力分析方法（理论的简化公式/有限元分析标定），可根据不同方法的自主选择实现测试结果间的校验，衡量数据的相对准确性。

（4）实现良好的人机交互。通过系统菜单、快捷按钮以及图表实现测试过程的控制及显示。

（5）实现时域信号及频域信号的图像及其历时数据的保存功能，为后期索力及桥梁整体的健康评估积累工程资料。

3.1 索力测试系统硬件设计

索力测试系统的最终运行效果（信号的准确性和完整性）依赖于各硬件设备集成后的综合性能。本系统采用性能价格比和灵活性相对较高的PC-DAQ的虚拟测试系统：选择便携快捷组装的NI-compactDAQ数据采集箱和NI9234采集模块；并采用USB数据连接线连接采集卡和PC机；索力信号则由压电加速度传感器拾取。

3.2 索力测试系统软件设计

LabVIEW是基于数据流的图形编程环境，较同类工具更具效率，其开发的程序可与其它工程测试设备实现无缝接合[6,7]，因此，本文选择LabVIEW作为拉索振动测试系统的数据采集及仪器控制工具。基于LabVIEW平台开发的索力测试系统程序根据软件工程学中“自顶向下，逐层细分”的原则设计。具体模块分解见图4，各功能模块间相互联系且相互独立，便于软件的开发、调试、修改、维护及日后软件的扩展。压力加速度传感器是原始的数据来源，NI9234采集与NI-compactDAQ数据采集箱在驱动程序作用下为系统提供真实的测试数据；根据实际工程需求，设置测试系统参数，包括信号接入、采样设置、通道标定、滤波设置、频率分析、拉索参数，然后可开始数据采样；对于采集到的时域、频域信息可以直接以图形、表格形式进行显示，也可以进行简单的滤波处理，关键的索力信号，可以根据解析计算、数值拟合的方式得到，这些都是采集、测试的结果。对于数所结果，系统以.dat文件格式进行保存，图形结果可以是bmp或jpg等常用格式，也可以将测试结果导出到Excel，以方便进一步的处理[8]，见表1。

表1 某拉索梁单元动力分析文件-频率索力结果表

针对设计程序的可执行性，对其进行试运行。于程序内部设置2通道的仿真信号：频率1 Hz，幅值为1的方波信号；频率为10 Hz，幅值为1的正弦波信号。两通道均施加幅值为1的均匀白噪声。程序接入模拟信号后，根据索力计算公式模式对通道1索力分析设置参数：长度40 m、线密度为48 kg/m、弹性模量为；同时根据索数值拟合模式对通道1选取与前参数条件一致拉索相应的动力分析文件（即表1）进行插值计算。程序运行结果见图5，信号可以用图形形象表达，也可以用表格进行精确的数值表达，图5（a）表示滤波前的时频域信息，频域信号用图形表达，图5（b）表示滤波后的时频域信息，频域信号用表格进行了数值表达。

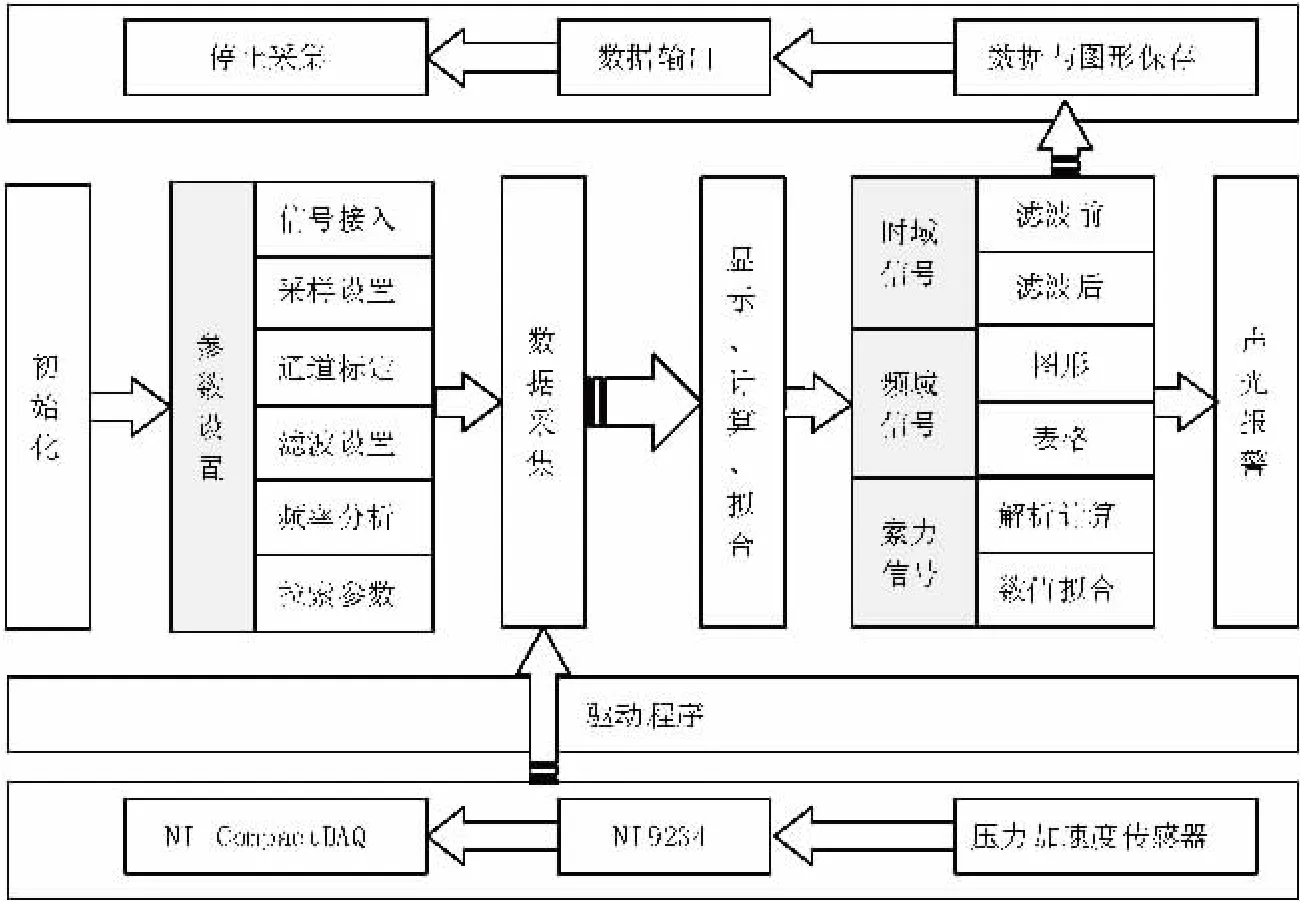
图4 索力测试系统软件设计模块示意图

图5 索力测试系统运行控制界面

3.3 索力测试系统验证

系统运行的可信度需通过对确定性拉索模型理论输出结果的符合程度进行验证[9]。该处建立重力作用下的水平索模型：拉索长度取100 m；拉索轴力分别取1×106N、2×106N、3×106N不等；拉索截面积取0.006 m2；拉索弹性模量取1.9×1011Pa；泊松比取0.167；密度为8 000 kg/m3；拉索惯性量在梁振动计算模式条件下取值2×10-6m4,在弦振动计算模式条件下取值0 m4。模型采用ANSYS内置的Link10单元。拉索两端节点均为铰支约束，将随机荷载以单点激励的方式作用于距拉索模型端部20 m处的节点上：随机荷载1的步长0.01 s，荷载历程60 s；随机荷载2的步长0.01 s，荷载历程20s；随机荷载3的步长0.1 s，荷载历程600 s；随机荷载4的步长0.1 s，荷载历程60 s。根据索模型的时程分析，获取激励条件下索

模型每隔10 m的节点上的位移时间数组序列，以此模拟传感器的时域信号，输入索力测试系统内置的FFT变换程序，得到频率结果，后通过索力-频率的数据分析的公式计算模块，得到相应的索力结果，将该值同有限元拉索模型事先设定的预加张拉力进行比较，借此对程序函数的可靠性进行验证。表2为不同工况下数值验证模型的程序分析结果。

根据表2，可见：

（1）各工况激励下的荷载偏差保持在5%左右，基本满足工程需要。该偏差一方面来自于数值模型的数值计算过程，另一方面受快速傅里叶变化的样本点数取值影响，此外，索自振频率与索力之间存在的平方关系也会使得最终索力计算结果偏差有所扩大。

表2 100 m拉索数值模型索力验证表

（2）根据测试系统的公式计算，梁振动模式公式结果与弦振动公式结果相近，符合数值拉索模型的基本力学特性，即抗弯刚度较其轴向张拉力可忽略。

（3）根据随机荷载激励的测试结果，激励时间步长为0.01 s下的索力值较激励时间步长为0.1 s下的索力值更大一些。提高测试中的采样频率，相应的测试结果将会偏安全，同时也可在一定程度提高测试精度。

4 结语

本文就索力测试系统开发进行系统整体的结构研究，具体结论如下：

（1）实际拉索特性各异，抗弯刚度、边界条件以及索长是影响拉索自振频率与索张力之间的主要因素。其中特定参数条件下的短索动力特性（10 m及以下）受其抗弯刚度及边界条件影响的偏差较同参数条件下的长索模型大。

（2）依据系统目标功能及综合性价比进行硬件设计，使之具有良好的便携操作性及功能维护性；根据系统需求分析进行程序设计，实现多通道信号输入、处理及显示，实现采集过程数据自动保存；针对结论1中不同拉索的测试问题，设计不同的频率、索力换算模式，包含一般索力解析表达模式和数值分析标定模式。

通过拉索的振动分析并结合LabVIEW平台的系统开发，可极大地满足实际不同拉索构件的测试需求，并为日后的系统维护及扩展提供良好的基础框架。

[1]Ignacio González.Study and Application of Modern Bridge Monitoring Techniques[J].TRITA-BKN,Bulletin 110,2011.

[2]Hikami Y,Shiraishi N.Rain_wind induced vibrations of cables in cable stayed bridge [J].J of wind Engineering and Industrial Aerdynainic,1988(29):409-418.

[3]邬喆华.磁流变阻尼器对斜拉索的振动控制[D].浙江杭州:浙江大学,2003.

[4]H.Max Irvine.Cable Structure[M].MIT PRESS,1981.

[5]徐宏,黄平明,韩万水.刚性短索索力计算及边界条件分析[J].长安大学学报（自然科学版）,2008,28(2):58-62.

[6]何晋,潘书文,朱西平.基于LabVIEW的桥梁监测系统设计与实现[J].成都信息工程学院学报,2015(2):176-179.

[7]龙华伟,顾永刚.LabVIEW 8.2.1与DAQ数据采集[M].北京:清华大学出版社,2008.

[8]傅理文.基于LabVIEW索力测试系统开发研究[D].浙江杭州:浙江大学,2010.

[9]唐浩,谭川,陈果.桥梁健康监测数据分析研究综述[J].公路交通技术,2014(5):99.

马鞍山长江公路大桥再获大奖

近日，2016～2017年度中国建设工程鲁班奖（国家优质工程）颁奖大会在京举行，马鞍山长江公路大桥荣获该奖。

马鞍山长江大桥项目路线全长36.274 km，其中长江大桥长11.209 km，概算总投资70.8亿元。项目在实施中，注重科技攻关，取得了包括设计方法、施工工法、施工设备、建设管理模式及安全管理成套技术、高品质混凝土技术等多方面原创性研究成果，形成了具有自主知识产权的多塔连跨缆索承重桥的建设管理成果,同时形成了完善的质量管理体系，有效提升了工程品质。混凝土结构物保护层合格率达到90%以上，钢结构探伤一次合格率超过99.9%，最终合格率为100%，构件制作与安装精度优于设计与规范要求。

项目先后获得乔治理查德森奖、中国公路学会科学技术奖特等奖、安徽省科学技术奖一等奖；取得23项国家专利，8项施工工法。项目于2013年12月建成通车，2016年7月通过交通运输部组织的竣工验收。

中国建筑工程鲁班奖创立于1987年，是国内建筑行业工程质量最高荣誉奖。鲁班奖作为全国建筑行业工程质量的最高荣誉奖，每年颁奖一次，授予中国质量品质卓越的工程。

U443.38

A

1009-7716（2017）12-0171-06

10.16799/j.cnki.csdqyfh.2017.12.048

2017-07-01

傅理文（1985-），女，浙江杭州人，工程师，从事结构有限元分析、水利水电工程设计工作。