基于高密度电阻率法的近地表工程岩体速度结构成像

赵 钊， 孟庆生， 韩 凯， 刘圣彪， 肖志广

(山东省海洋环境地质工程重点实验室(中国海洋大学),青岛 266100)

基于高密度电阻率法的近地表工程岩体速度结构成像

赵 钊， 孟庆生*， 韩 凯， 刘圣彪， 肖志广

(山东省海洋环境地质工程重点实验室(中国海洋大学),青岛 266100)

纵波速度划分岩体等级对地下空间工程具有重要的意义。基于Faust公式，建立了表征电阻率和纵波速度的超定方程组，并研究了β系数的确定方法。通过数值模拟手段，验证了近地表岩体纵波速度成像方法的有效性。结果表明，该方法对层状地层、含断层、高低阻地质异常等复杂地质结构均具有良好的反映能力。应用实例表明，计算值与实测值之间的误差小于8.7%，可为工程勘察提供可信的纵波速度。

高密度电阻率； Faust公式； 速度成像

0 引言

随着我国城市化的高速发展，人均可利用的地面资源日益匮乏。为解决这一矛盾，修建城市地铁，地下制作车间、电站、人防等地下空间工程已成为发达国家城市建设的必然选择[1]。但是由于地下地质条件的复杂性，给地下空间工程建设带来了严峻挑战[2]。为合理建设地下工程，需要在勘察阶段详细了解岩体的工程特性。其中岩体等级的准确划分对选择合理的设计方案、施工方法，以及确定工程结构荷载等具有重要的意义。

在岩土工程领域，岩体的等级主要以围岩中的纵波速度作为划分标准[3-4]。传统获取岩石纵波速度的方法是通过钻孔取芯，然后对岩芯进行室内测试获取。虽然该方法可以直接获取岩体的纵波速度，但受场地条件和投入的限制不能大规模开展。近年来，一些以物探方法为主的岩体纵波速度测试手段得到了广泛应用，常用的有折射波法[5]、瑞利面波法[6]，这类方法具有无损、快速和经济的优点[7]。然而，在城市环境中开展上述以弹性振动为基础的方法时，由于外界震动干扰源多，常常无法获得高分辨率的地震数据，导致无法获得准确的纵波速度。

高密度电阻率法是以地下介质的电性差异为基础的一类方法，可依据电阻率的变化定性确定岩体的分界面，在地质勘察和地质灾害探测中发挥了重要的作用[8]。此外，通过对数百万英尺测井资料的分析证实，电阻率与地下介质的纵波速度具有良好的关系[9]。将两种手段结合，可获得工程岩体的纵波速度，进而为岩体等级划分提供依据。笔者基于Faust公式，结合高密度电阻率法，并利用少量钻孔标定的方法，探讨一种工程岩体速度建模新方法，为地下空间工程中岩体等级划分提供有利的工具。

1 近地表速度建模理论

1.1 Faust 公式[10]

上世纪40年代后期和50年代中期，Faust分析了数百万尺的测井资料，将电阻率与速度进行对比，证实了岩石的纵波速度与埋深和岩石的电性(电阻率)有关，即Faust方程，如式(1)所示。

V=AZTR1/6

(1)

式中：A为常数；Z为深度(m)；T为岩性因子；R为电阻率(Ω·m)。

结合阿尔奇(Archie)经验公式[11]和威利(Wyllie)时间平均方程[12]，可将Faust公式改写为式(2)。

v=kραHβ

(2)

式中：v为纵波波速(m/s)；k为与岩石性质有关的经验常数；H为深度(m)；α、β为与地层有关的经验常数；ρ为电阻率(Ω·m)。在没有声波测井资料但有电阻率数据的地区，式(2)可以用来获取岩体的纵波速度。

1.2 基于广义逆法的速度反演

将Faust公式的两边取对数可得式(3)。

lgv=lgk+αlgρ+βlgH

(3)

式(3)反映出的lgv、lgρ和lgk的关系只是近似的线性关系,不能精确反映速度与电阻率和深度之间复杂的非线性关系。为此，笔者以lgρ和lgH的高阶多项式来拟合地层速度，在每一深度如式(4)所示。

v=a1lgρHβ+a2(lgρHβ)2+a3

(4)

写成矩阵形式为

V=XA

(5)

式(5)中：

V=|v1,v2,v3,…,vn|T|

A=|a1,a2,a3|T

对于方程中的系数β，可以通过实测场地钻孔位置的波速、电阻率和深度资料，直接拟合分析v与lgρHβ之间的关系求得。式(4)为超定方程组，采用广义逆法可以求出系数α1、α2、α3。在无钻孔的位置，利用测得的电阻率剖面数据插值每一深度段的电阻率，再利用求得的系数即可求出纵波速度。

对于求解出的各深度的速度值来说，可能会出现比实际波速大或小的情况。我们将作如下处理，首先对钻孔波速测试数据在深度方向进行与电阻率数据等密度的插值，得到一组波速数据

V1=|v1,v2,v3,v4|T

(6)

设利用电阻率成像算法计算得到的波速数据为v2，两者之差为

▽V=V2-V1

(7)

令m=▽V/V1,则权系数定义为

W=1-m

(8)

修正后的波速为式(9)。

V加权=W·V

(9)

2 有效性验证

2.1 均匀地层

设计层状均匀地层，地电模型参数如表1所示。

表1 均匀层状地电模型

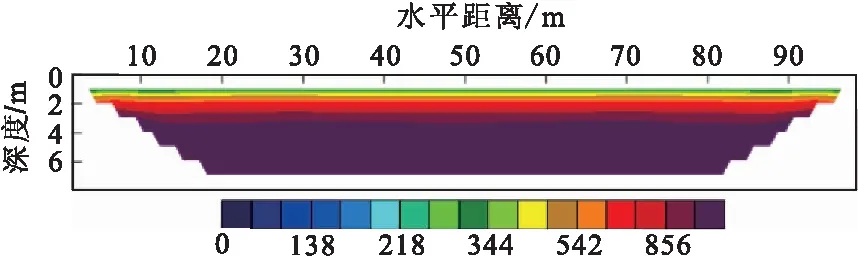
图1 均匀地层反演模拟结果Fig.1 The inverse modeling result of layered formation

利用Wenner装置对上述模型正、反演后的结果见图1，装置参数，电极为101个，电极间距为1 m。

利用公式(5)求得的方程系数为β=0.308 5,a1=-235.821 1，a2=52.435 0，a3=867.970 7,进而求得剖面中其他各点随深度变化的纵波速度，其反演速度剖面见图2。

由图2可见，电阻率波速也呈现良好的正相关关系，各层波速与模型基本一致并随深度增加而增大。

2.2 含高低阻带地层

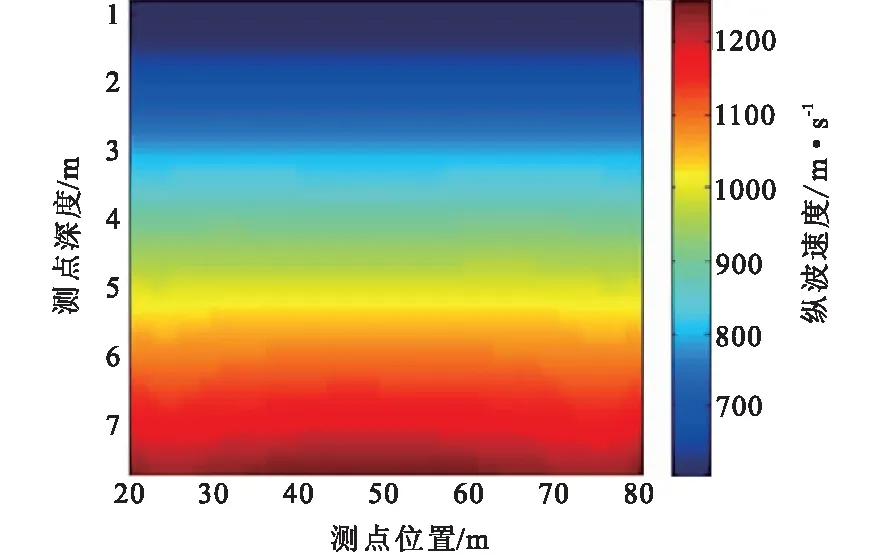
图2 均匀地层纵波速度成像剖面Fig.2 The velocity imaging of layered formation

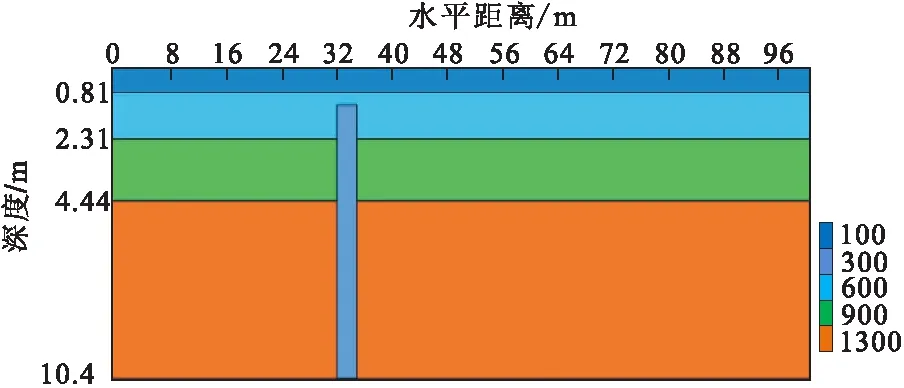
图3 含高低阻地层地电模型Fig.3 The abnormal formation with low or high resistance model

均匀地层是一种十分理想的地质模型，实际的地层是非常复杂的，常常含有断层、溶洞等不良地质体，总体上可分为高阻体和低阻体两类。为验证速度建模方法在复杂地质条件下的适用性，分别在均匀地层模型中设立高阻区和低阻区(图3)，其电阻率分别为3 000 Ω·m和300 Ω·m。

利用上述方法，获得相应的电阻率剖面(图4)和速度模型(图5)。

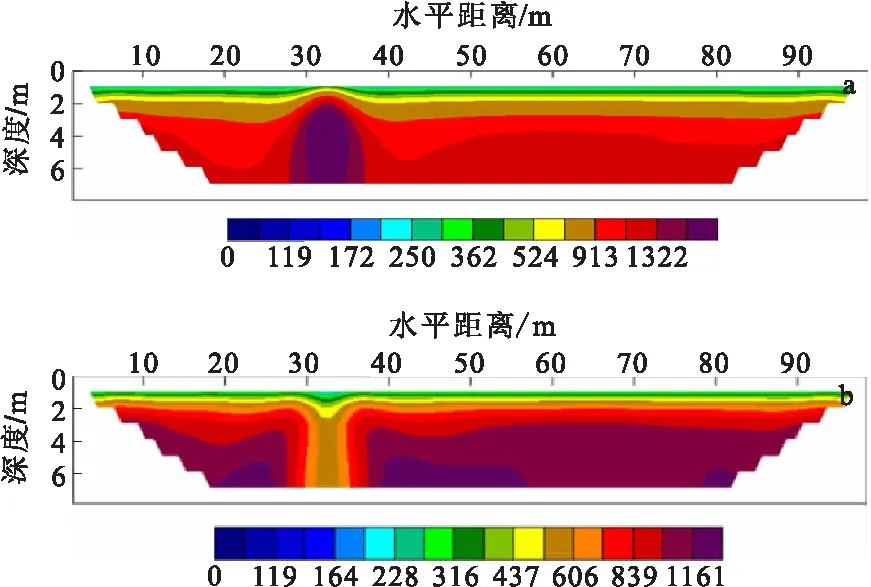
图4 高阻、低阻模型电阻率剖面Fig.4 The resistivity model profile of abnormal formation whth high and low resistance(a)高阻模型；(b)低阻模型

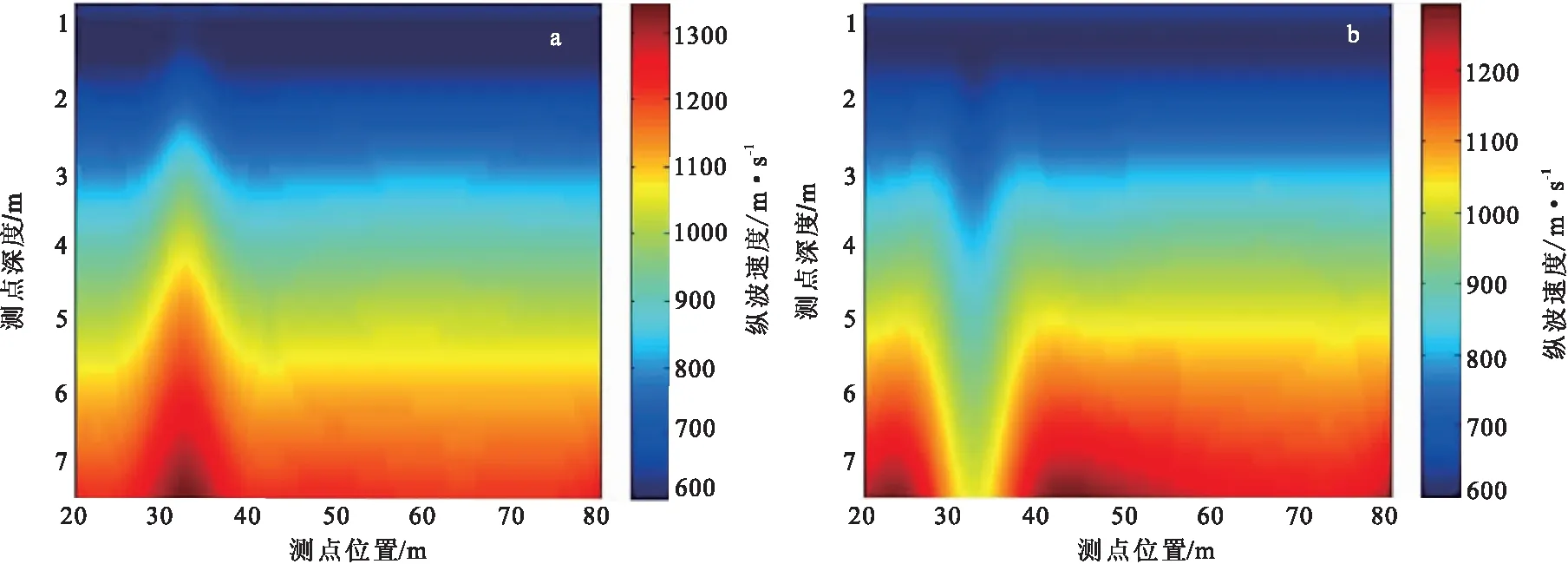
图5 高阻、低阻反演速度成像剖面Fig.5 The inverse velocity image of high and low resistance(a)高阻；(b)低阻

由图5可知，在模型的高、低阻异常处，波速值也有明显地变化，分别表现为高波速异常和低波速异常，与模型中设计的异常位置非常吻合。证实了该方法对复杂的地层具有很好的表现能力。在实际的工程应用中，可以根据波速的变化推断异常体的存在。

3 应用实例

3.1 试验场地概况

试验选取某工程场地进行。由浅到深地层依次为人工填土(0.5 m ～5.0 m)，安山岩强风化带、中等风化带和微风化带。为获得方程系数，在场地中的一条高密度电阻率探测测线上分别布设了Z38、Z39和Z40三个钻孔，并在孔内测量各层的声波速度(表2)。本次试验中用Z38号孔作为波速反演的参照孔，Z39和Z40孔作为验证孔。

高密度电阻率法试验采用吉林大学工程技术研究所生产的E60DN高密度电法仪，测量装置为Wenner装置，电极数 为64个，电极距为2.0 m，采集层数为14层。试验数据经反演后的剖面见图6。

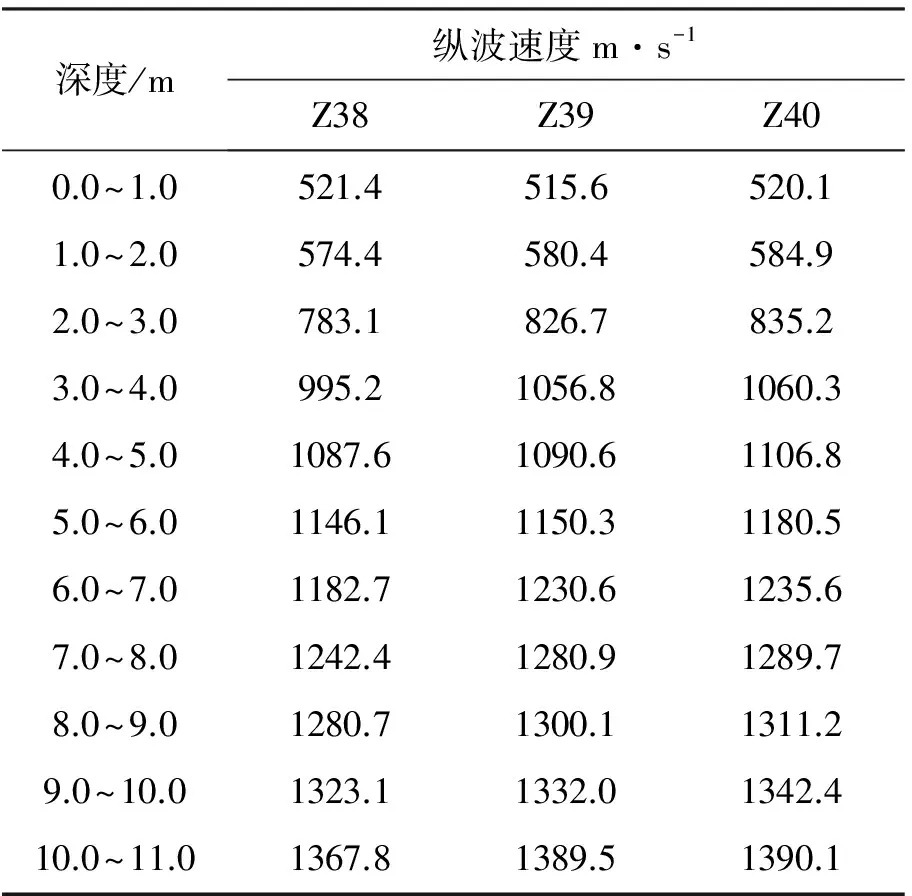
表2 试验场地孔内纵波速度

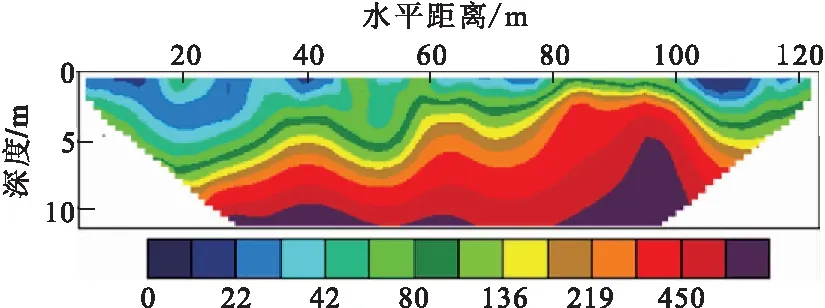
图6 实际场地高密度电阻率法探测剖面Fig.6 The ground profile by the high density resistivity method

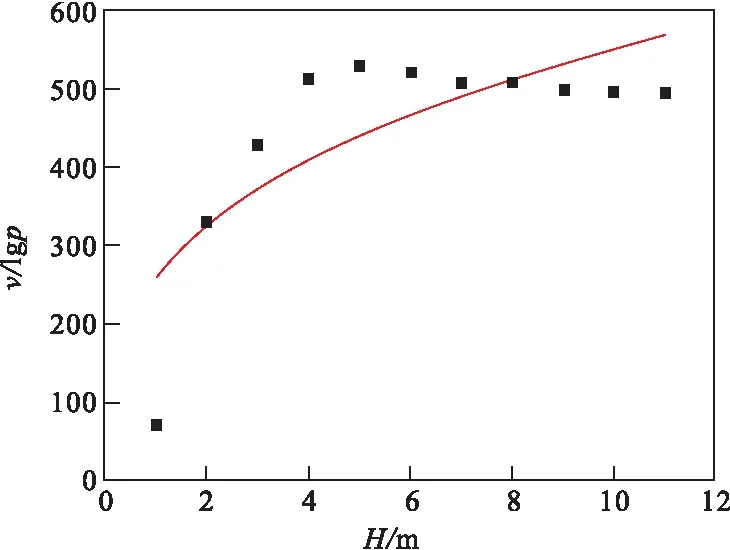
图7 深度H与v/lg ρ拟合曲线Fig.7 The line of H and v/lg ρ

3.2 岩体速度结构成像

本次试验分别获得了0.50 m、1.50 m、2.55 m、3.70 m、4.98 m、6.37 m、7.91 m、9.60 m及11.46 m深度处的电阻率值。而波速测试的深度点分别为1.0 m、2.0 m、3.0 m、4.0 m、5.0 m、6.0 m、7.0 m、8.0 m、9.0 m、10.0 m、11.0 m，二者不一致。为此，需将电阻率数据进行插值，得到与波速数据点处相对应的电阻率值。

在得到Z38钻孔处的波速数据及电阻率数据后，使用origin软件中Allometric型幂指数拟合方式求取系数，拟合曲线见图7，其中横坐标为H，纵坐标为v/lgρ，求得的β系数为0.33。

利用Z38孔处波速、电阻率和β系数，将数据应用于超定方程组中，求得系数a1=-785.526 8，a2=-76.570 6，a3=-591.128 8。进而获得各测点不同深度的纵波速度剖面(图8)。

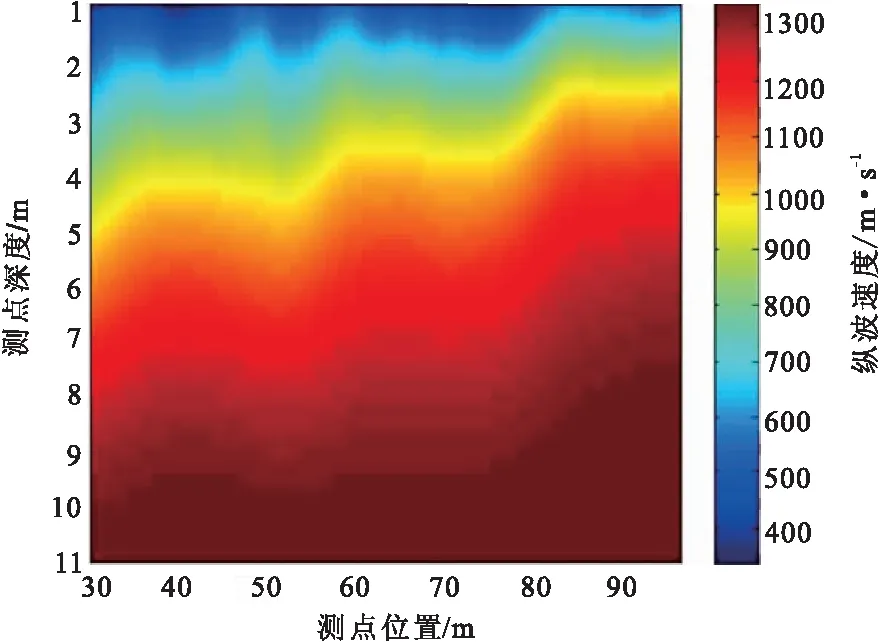
图8 场地速度结构剖面图Fig.8 The velocity structure section in the ground

3.3 误差分析

为验证基于Faust公式速度建模方法的准确性，将获得的波速与Z39、Z40钻孔处测量的波速进行比较(表3)。通过对反演电阻率数据与Z39、Z40孔实测波速的对比发现，反演成像后的波速数据与计算数据具有较高的一致性，最大误差为8.7%。个别深度点波速出现过大或过小的原因是由于本试验中拟合β系数的数据点较少，从而导致的拟合精度不高。

4 结论

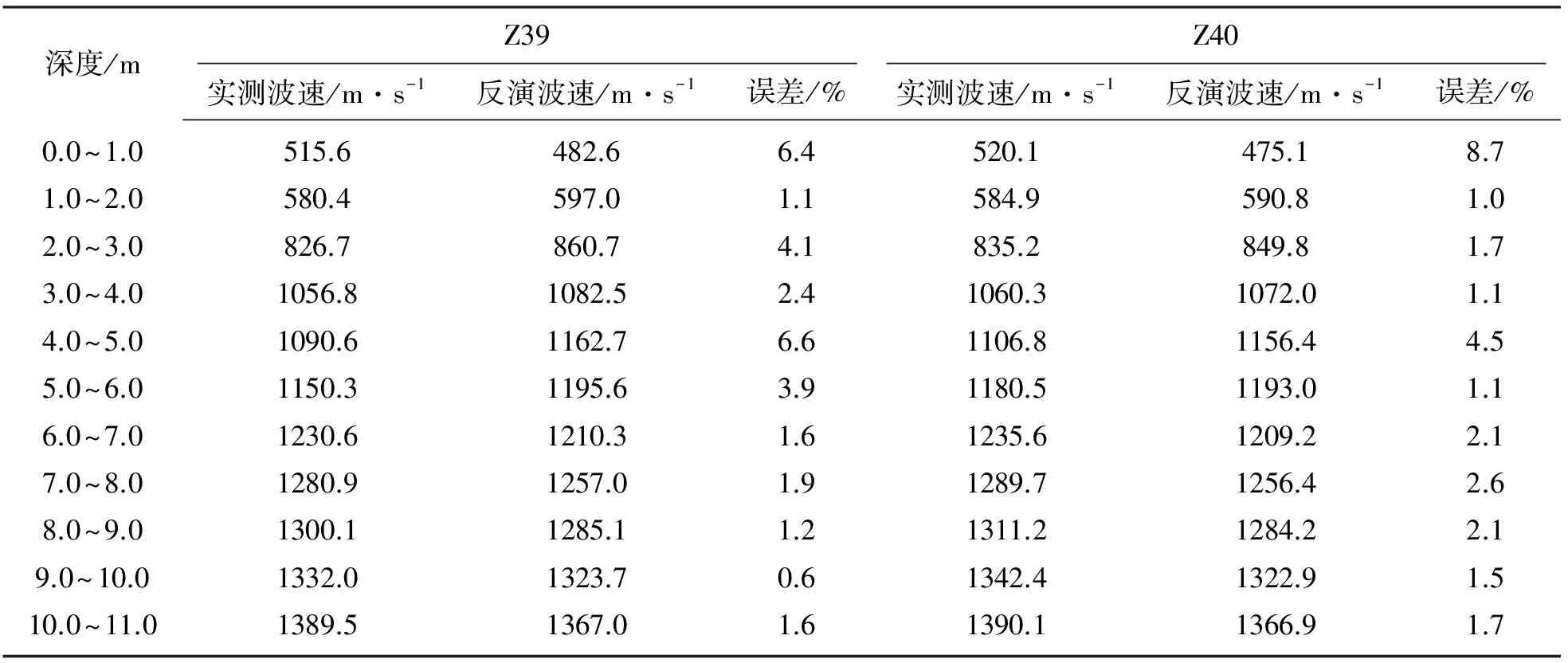
表3 反演成像速度与Z39、Z40孔测量波速对比

1)理论与实际结果证实，基于Faust公式和高密度电阻率法的纵波速度建模技术，对均匀地层、含低阻异常体地层和含高阻异常体地层均具有良好的适用性。

2)实际场地应用结果表明：在该案例中，相对误差不超过8.7%。利用电阻率数据反演出的纵波速度剖面与验证钻孔揭示的纵波速度具有良好的一致性。

3)笔者对夹层、互层等电阻率突变地质条件下未进行验证，在今后的工作中需进一步验证。

[1] 赵晋友，黄松.城市地下空间开发面临的机遇与挑战[J].地质与勘探，2013，49(5)：0964-0969.

ZHAO J Y，HUANG S．Opportunities and challenges in the development of urban underground space[J].Geology and Exploration，2013，49( 5) : 0964-0969．(In Chinese)

[2] 万汉斌.城市高密度地区地下空间开发策略研究[D].天津：天津大学，2013.

WAN H B. The strategy research on urban underground space in high-density area [D]. Tianjin: Tianjin University,2013. (In Chinese)

[3] 王洪勇. 关于应用弹性波速度划分隧道围岩类别的认识[J]. 隧道建设, 2000, 20(3): 19-25.

WANG H Y. Some knowledge about the separation of tunnel surrounding rock via the elastic wave velocity [J].Tunnel Construction,2000,20(3):19-25. (In Chinese)

[4] 许广春. 大地电磁测深进行隧道围岩分级的可行性研究[J].铁道工程学报，2010,27(8):83-86.

XU G C. Research on feasibility of sorting surrounding rock of tunnel with telluric electromagnetic sounding [J]. Journal of Railway Engineering Society, 2010,27(8):83-86. (In Chinese)

[5] 陈爱萍，邹文，何光明，等.初至波地震层析成像中自动生成初始速度模型的方法研究[J]. 物探化探计算技术,2014,157(5):583-586.

CHEN A P, ZOU W, HE G M, et al. Automatically building the initial velocity model in first-arrival seismic tomography [J]. Computing Techniques for Geophysical and Geochemical Exploration, 2014,157(5):583-586. (In Chinese)

[6] 周竹生，刘喜亮，熊孝雨.弹性介质中瑞雷面波有限差分法正演模拟[J].地球物理学报，2007,50(2)：567-573.

ZHOU Z S, LIU X L, XIONG XY. Finite-difference modelling of Rayleigh surface wave in elastic media [J]. Chinese Journal of Geophysics, 2007, 50(2):567-573.(In Chinese)

[7] 程红杰，胡祥云，张荣,等.近地表地球物理发展状况综述[J].工程地球物理学报，2005,2(1):73-76.

CHENG H J, HU X Y, ZHANG R, et al.The development of the near surface geophysics [J].Chinese Journal of Engineering Geophysics, 2005, 2(1):73-76. (In Chinese)

[8] 严加永，孟贵祥，吕庆田，等.高密度电法的进展与展望[J].物探与化探，2012,36(4)：576-584.

YAN J Y, MENG G X, LV Q T, et al. The progress and prospect of the electrical resistivity imaging survey [J].Geophysical and Geochemical Exploration, 2012,36(4):576-584. (In Chinese)

[9] FAUST L Y. A velocity function including lithologic variation [J]. Geophysics, 1953, 18(2): 271-288.

[10] FAUST L Y. Seismic velocity as a function of depth and geologic time [J]. Geophysics, 1951, 16(2): 192-206.

[11] 孙建国. 阿尔奇公式：提出背景与早期争论[J].应用物理学，2007,22(2)：472-486.

SUN J G. Archie’s formula: historical background and earlier debates[J].Applied Physics,2007,22(2)：472-486. (In Chinese)

[12] WOOD W T, STOFFA P L, SHIPLEY T H. Quantitative detection of methane hydrate through high-resolution seismic velocity analysis [J]. J Geophys Res,1994, 99: 9681-9695.

Rockmassvelocityimagingbasedonhighdensityresistivitymethodinnearsurfaceengineering

ZHAO Zhao， MENG Qingsheng*， HAN Kai， LIU Shengbiao， XIAO Zhiguang

(Shandong Provincial Key Laboratory of Marine Environment and Geological Engineering (Ocean University of China), Qingdao 266100, China)

It is meaningful to the underground engineer that the P-wave velocity is divided by the rock grade. According to the Faust formula, the overdetermined equation of resistivity data and P-wave velocity is built, and the way of β determination is researched. Validity of this rock mass velocity map imaging way is proved according to the numerical simulation. The result shows this way is useful to the complex geological structure like layered formation, fault, and abnormal formations with high or low resistance. The application example shows the error of the calculate and the measure results is less than 8.7%, the P-wave velocity calculated by this way is credible to the geotechnical investigation and surveying.

high density resistivity; Faust formula; velocity imaging

2016-11-13 改回日期： 2017-02-21

国家重大科研仪器研制项目(41427803)

赵钊(1994-)，男，硕士，主要从事环境工程地球物理探测方面的研究工作，E-mail：705586405@qq.com。

孟庆生(1972-)，男，副教授，主要从事环境工程地球物理探测方面的教学和研究工作，E-mail：sdmengs@163.com。

1001-1749(2017)06-0742-06

P 631.3

A

10.3969/j.issn.1001-1749.2017.06.05