汽车碰撞试验中碰撞过程的运动及力学性能

王家顺, 安 琦

(华东理工大学机械与动力工程学院,上海 200237)

汽车碰撞试验中碰撞过程的运动及力学性能

王家顺, 安 琦

(华东理工大学机械与动力工程学院,上海 200237)

以汽车碰撞试验为研究对象,分析归纳了摩擦力做功及阻挡杆变形能的计算方法,根据能量守恒的原则,给出了碰撞过程的能量平衡模型,构建了对碰撞过程中滑车的运动以及阻挡杆的变形进行计算的数学模型,并提出了一种利用计算机对该模型进行计算求解的计算方法。以Matlab为计算工具,编制了计算程序,结合一个具体的算例,研究滑车质量、初始碰撞速度、内侧柱销中心距、阻挡杆截面尺寸等因素对滑车位移、冲撞力、速度、以及减速度的影响规律,得到了相应的变化曲线,并对其进行了分析,得出了有益的结论。

碰撞试验; 减速装置; 力学建模; 运动性能; 力学性能

在汽车安全装置的开发测试过程中需要进行大量的汽车碰撞试验,主要包括实车碰撞试验和滑车碰撞试验[1]。滑车碰撞试验具有试验费用低、准备周期短等优点,故应用较为广泛。

碰撞减速装置是该类试验的核心部件,其原理是通过滑车的碰撞头冲撞阻挡杆,使其变形,从而形成迅速停车效应,并且滑车的减速度波形需满足规范要求。实际应用中,由于缺乏理论指导,设计人员往往需要进行大量的试验,才能获得所需要的减速度波形,不仅效率低,而且难以把握。

对于汽车碰撞试验中的碰撞问题已有很多研究。胡玉梅等[1]对减速装置中钢板的排列与减速度波形的关系进行了研究,并总结出该类装置钢板的布置方法;曹立波等[2-3]利用LS-DYNA研究碰撞过程中钢板变形,得出截面尺寸等参数对滑车减速度的影响; Massenzio等[4]通过建立减速装置的力学模型来求解碰撞过程滑车减速度的大小,但是该模型仅考虑了钢板塑性变形的影响,模型过于简化;Giavotto等[5]利用试验测试和有限元仿真的方法验证了利用钢条塑性变形来吸收滑车动能的可行性,并建立数学模型,利用遗传算法研究如何利用钢条布置来获得期望的减速度波形;葛如海等[6]通过仿真研究,分析了钢筋类型等参数对减速过程的影响;张慧云等[7]根据试验经验,总结出复现不同减速度波形时钢筋的摆放方式;Xu等[8-9]对薄壁管结构的碰撞性能进行了仿真研究,并得出不同参数对该结构碰撞性能的影响;Jimenez等[10]仿真研究蜂窝铝机械块的吸能效果,结果显示该装置对改善液压型减速装置的初始减速度波形有较好效果。这些研究主要是通过有限元软件对碰撞过程中的减速装置进行研究,对碰撞过程中滑车的减速度变化等缺少定量分析。

本文以碰撞试验台为研究对象,对碰撞过程的运动和阻挡杆的变形进行力学分析,建立了相关力学模型,通过数值计算,研究了滑车质量、初始碰撞速度、内侧柱销中心距、阻挡杆的截面尺寸等因素对碰撞过程中滑车减速度、停车位移等参数的影响。

1 碰撞过程的力学建模

1.1 汽车碰撞试验原理

利用弹性绳作为弹射介质的汽车碰撞试验台模型如图1所示,其工作原理为:卷扬机拖动滑车沿轨道向后运动,同时滑车拉伸弹性绳进行储能。当滑车运动至释放位置时,由释放装置释放滑车,滑车在弹性绳的拉力下加速运动,直至弹性绳恢复原长,随后滑车与减速装置进行碰撞,通过检测试验假人在减速过程中各部位的伤害值来评价汽车安全装置对汽车乘员的保护性能。

碰撞过程中,滑车的碰撞杆头部与阻挡杆接触,并且推动阻挡杆向前运动,此时,阻挡杆在柱销处以及碰撞杆头部倒角处被迫发生塑性弯曲变形。碰撞过程中不同时刻的碰撞状态如图2所示。

图1 碰撞试验台模型Fig.1 Model of collision test bench

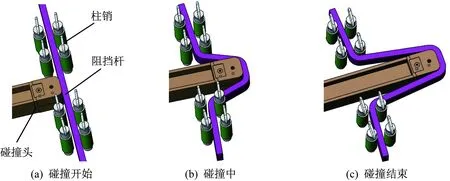
图2 不同时刻的碰撞状态Fig.2 Collision state at different time

1.2 碰撞过程的力学分析

碰撞过程中,滑车动能迅速减小,转变成其他形式的能量而被逐渐耗散。为了便于分析,作如下假设:

(1) 忽略发热等因素的影响;

(2) 滑车车轮与轨道之间的滚动摩擦阻力因子、阻挡杆与柱销之间的滑动摩擦因子为定值;

(3) 碰撞过程中,碰撞杆头部与阻挡杆始终保持接触;

(4) 碰撞结束时,滑车无回弹运动;

(5) 碰撞过程阻挡杆只发生塑性变形,忽略其在变形过程中的伸长量;

(6) 忽略应变速率对材料性能的影响,塑性变形过程中应力-应变之间的本构关系简化为线性强化刚塑性模型。

碰撞过程中,滑车水平方向受力分析如图3所示。m为滑车质量,F′为阻挡杆对滑车上碰撞杆施加的力,在F′作用下滑车迅速减速,直至停止运动;Ff为滑车车轮与轨道之间的滚动摩擦力,运动过程中,车轮与轨道之间摩擦力做功为Wf1。

图3 滑车受力分析Fig.3 Mechanics analysis of sled

碰撞过程中,阻挡杆受力分析如图4所示。其中,F为碰撞杆对阻挡杆施加的力,FN1、FN2、FN3、FN4为阻挡杆在柱销处的支反力,Ff1、Ff2、Ff3、Ff4为阻挡杆与柱销之间的摩擦力。

将减速装置看作近似完全对称,计算得

(1)

(2)

运动过程中,摩擦力Ff1、Ff2、Ff3、Ff4做功用Wf2表示。

图4 阻挡杆受力分析Fig.4 Mechanics analysis of block bar

对于滑车和阻挡杆组成的系统,F和F′是一对作用力和反作用力。根据假设分析可知,碰撞过程中,滑车的动能主要通过以下3种方式耗散:

(1) 滑车与轨道之间的摩擦力做功Wf1;

(2) 阻挡杆与柱销之间的摩擦力做功Wf2;

(3) 阻挡杆发生塑性变形所需要的变形能Wp。故碰撞过程中,某一个时刻滑车速度由速度V1减至速度V2时,根据能量守恒定律,可得能量平衡式

(3)

1.3 摩擦力做功及阻挡杆变形能

1.3.1 滑车与轨道之间摩擦力做功 在运动过程中,滑车与轨道通过4个圆柱形钢制车轮与轨道接触,假设滑车车轮与轨道之间的滚动摩擦阻力因子为μ1,那么运动过程中,滑车单个车轮所受摩擦力为

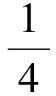
(4)

如图5所示,在滑车由速度V1减速至V2,滑车移动距离为L的过程中,滑车与轨道之间摩擦力做功

Wf1=4FfL=μ1mgL

(5)

1.3.2 变形协调关系 为计算碰撞过程中各因素所消耗滑车动能的量,需要明确滑车位移、柱销处阻挡杆弯曲变形量、弯曲角度之间的变形协调关系。为简化计算模型,假设在运动过程中,柱销之间的阻挡杆不发生偏转,其变形示意图如图5所示。

图5 阻挡杆变形示意图Fig.5 Diagram of block bar deformation

由图5中的几何关系,可得

(6)

(7)

(8)

故单侧柱销处阻挡杆弯曲变形量

(9)

(10)

(11)

1.3.3 阻挡杆与柱销之间摩擦力做功计算 根据图3滑车受力分析图,由牛顿第二定律可得

Ma=F′+4Ff

(12)

其中,a为滑车的加速度。由式(4)、 (12)可得

F′=Ma-4Ff=Ma-μ1Mg

(13)

假设阻挡杆与柱销之间的滑动摩擦因子为μ2,故当阻挡杆移动一个微量距离dl时,柱销与阻挡杆之间的摩擦力做功为

dwf2=μ2(FN1+FN2+FN3+FN4)dl=

(14)

在滑车由速度V1减至V2、阻挡杆在柱销中移动距离为l的过程中,阻挡杆与柱销之间的摩擦力做功为

(15)

1.3.4 阻挡杆弯曲变形能的计算 为计算碰撞过程中阻挡杆变形所需要的能量,首先要明确塑性变形时,材料内部应变能密度的大小。

宽度为b的阻挡杆发生如图6所示的弯曲变形时,由力学知识可知,与其中性层距离为y(-b/2≤y≤b/2)处的应变为

(16)

式中,ρ为曲率半径。

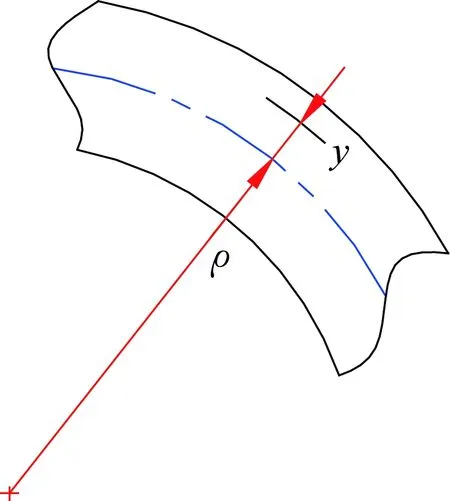
图6 弯曲变形Fig.6 Bending deformation

由文献[11]可知,对于线性强化刚塑性模型,材料在塑性变形过程中,其应力与应变之间的本构关系为

σ=σs+Hε

(17)

式中:σs为材料的屈服强度;H为材料的切线模量。

由文献[12]可知,阻挡杆塑性变形时的应变能密度为

(18)

碰撞过程中,阻挡杆会在柱销处以及碰撞杆头部倒角处发生塑性变形。将整个碰撞过程滑车位移离散为若干个长度为dL的区间,由图5可知,该位移区间内,有长度为dl的阻挡杆通过O1A截面在柱销处发生弯曲变形,所需变形能为dWp1;同时有长度为dl-ρ1dθ的阻挡杆脱离柱销,随台车向前运动的过程中又恢复至原状,该段长度的阻挡杆发生变形所需变形能量为dWp2;在碰撞杆头部的单侧倒角处有长度为ρ2dθ的阻挡杆发生弯曲变形,所需变形能为dWp3。假设阻挡杆宽度为b,高度为h,那么对于长度为dl的阻挡杆弯曲变形所需要的能量为

(19)

将式(16)、(18)带入式(19)并积分可得

(20)

同理可得

(21)

(22)

滑车由速度V1运动至速度V2的过程中,滑车移动距离为L,单侧柱销处阻挡杆弯曲变形量为l、弯曲角度为θ。则该过程中,单侧柱销处阻挡杆弯曲变形所需要的变形能为

(23)

同理可得阻挡杆脱离柱销后恢复变形所需要的变形能为

(24)

碰撞杆头部单侧倒角处阻挡杆变形所需要的变形能为

(25)

减速装置完全对称,所以碰撞过程中阻挡杆弯曲变形所消耗的总能量为

Wp=2(Wp1+Wp2+Wp3)

(26)

1.4 力学模型求解方法

为分析碰撞过程中滑车速度、减速度等参数的变化情况,本文采用如下方法对模型进行求解:

(1) 给定滑车质量M、柱销半径R1、碰撞杆头部倒角半径R2、阻挡杆截面尺寸b、h,柱销圆心与碰撞杆头部倒角圆心的距离l0以及柱销之间的中心距l1、l2;

(2) 给定初值l=0、L=0、θ=0,设定滑车微小位移dL的大小,以及滑车初始碰撞速度V1的值;

(3) 计算滑车在当前状态下滑车移动dL时摩擦力做功Wf1、Wf2及阻挡杆弯曲变形所需要的变形能Wp,根据式(3)计算滑车移动dL后的速度V2;

(4) 根据式(27)、(28)求解该位移区间内滑车的减速度an、时间tn,并计算本次运动结束时L、l、θ的大小,作为下次运动的初始状态;

(27)

(28)

(5) 判断V2≥10-8是否成立。若成立,将V2作为下一位移区间的初始碰撞速度V1,重复步骤(3)～(5),若不成立,绘制相应的变化曲线,结束

计算。

按照上述的计算方法,利用Matlab编程计算,其过程如图7所示。

图7 计算流程图Fig.7 Calculation flow chart

2 算例研究

根据以上计算方法,以某一具体的碰撞试验台为算例进行计算研究,并分析各参数对滑车碰撞过程的影响。滑车碰撞试验的主要参数见表1,阻挡杆材料为Q235,切线模量为6 100 MPa,截面为宽度b=20 mm、高度h=60 mm的矩形截面。

表1 滑车碰撞试验参数

图8示出了初始碰撞速度为60 km/h,滑车质量为m时对碰撞过程的影响。从图中曲线可以看出:质量越大,碰撞位移越大,不同质量的滑车在碰撞过程中,其位移曲线变化大致相同,呈非线性变化;滑车质量对冲撞力影响很小,碰撞过程中,冲撞力先增大,然后保持基本不变,不同质量的滑车,其碰撞力变化曲线几乎重合,从碰撞力变化曲线局部放大图可以看出,随着滑车质量的增加,碰撞过程中最大碰撞力稍有增加;滑车质量越大,滑车速度变化越慢,在碰撞过程中达到的最大减速度越小。

图9示出了滑车质量M=900 kg时,滑车初始碰撞速度对碰撞过程的影响。从图中曲线可以看出:初始碰撞速度越大,碰撞位移越大,位移曲线变化越快,达到最大冲撞力所需要的时间越短,但其对最大冲撞力影响较小;不同的初始碰撞速度,滑车的速度变化曲线大致相同;初始碰撞速度越大,滑车的减速度变化越快;初始碰撞速度对滑车所能达到的最大减速度影响不大。

图10示出了初始碰撞速度为60 km/h时,内侧柱销中心距l2对碰撞过程的影响。从图中的曲线可以看出:中心距越大,碰撞位移越大,冲撞力变化越慢,但其对最大冲撞力影响较小;中心距越小,滑车速度变化越快,滑车的减速度越大,但是中心距的变化对滑车所能达到的最大减速度影响不大。

图8 滑车质量对碰撞过程运动参数的影响Fig.8 Influences of the sled quality on the motion parameters during collision

图9 初始碰撞速度对碰撞过程运动参数的影响Fig.9 Influences of the initial collision speed on the motion parameters during collision

图11示出了初始碰撞速度为50 km/h,阻挡杆矩形截面宽度b不变时,截面高度h对碰撞过程的影响。由图中的曲线可以看出:阻挡杆截面高度越大,碰撞位移越小,冲撞力变化越快,且达到的最大冲撞力越大,碰撞过程滑车速度变化越快,得到的最大减速度越大。

图11 截面高度对碰撞过程运动参数的影响Fig.11 Influences of the cross section height on the motion parameters during collision

3 结 论

(1) 以汽车碰撞试验为研究对象,对碰撞过程中滑车的运动以及阻挡杆的变形进行了分析,根据能量守恒定律得到了碰撞过程的力学模型,并对模型中摩擦力做功及阻挡杆变形能建立了计算模型;构建了一种能够对碰撞过程的位移、速度、减速度以及冲撞力进行计算的算法,以Matlab为计算工具进行编程,实现了对碰撞过程的运动学参数和冲撞力进行定量计算。

(2) 利用所建立的计算模型,以某一具体的汽车碰撞试验台为对象进行了算例研究,研究了滑车质量、初始碰撞速度、内侧柱销中心距、阻挡杆截面尺寸等参数对滑车碰撞过程的影响,得出了一系列曲线。研究结果表明:在其他参数保持不变的情况下,滑车的碰撞位移曲线变化大致相同,呈非线性变化,且滑车位移随滑车质量的增加而增大,随初始碰撞速度的增加而增大,随内侧柱销中心距的增加而增大,随阻挡杆截面高度的增加而减小;阻挡杆截面高度对滑车的最大冲撞力影响较大,其余参数对最大冲撞力影响较小;碰撞过程中,滑车质量越大,速度变化越慢,阻挡杆截面高度越大,速度变化越快,初始碰撞速度以及内侧柱销中心距对滑车速度变化影响较小;滑车的最大减速度随滑车质量的增大而减小,随初始碰撞速度的增加而增大,随柱销中心距的增大而减小,随阻挡杆截面高度的增加而增大。

[1] 胡玉梅,曾繁林,张科峰,等.台车试验中钢板布置的研究[J].汽车工程,2012,34(6):496-501.

[2] 曹立波,钟志华,白中浩,等.台车碰撞试验用机械缓冲吸能装置研究[J].汽车工程,2002,24(3):228-230.

[3] ZHANG Xu,JIANG Qi,LI Liwei,etal.Study on the crash energy absorption structure of a vehicle simulator crash testing equipment[J].Key Engineering Materials,2011,486:266-269.

[4] MASSENZIO M,MAUPAS A,BENNANI A,etal.Study of a device for controlling the pulses of sled testing[J].International Journal of Crashworthiness,2007,12(3):311-318.

[5] GIAVOTTO V,ANGHILERI M,CASTELLETTI L M L,etal.A braking system for tests with a prescribed deceleration pulse[J].Experimental Mechanics,2010,50(7):915-930.

[6] 葛如海,穆青,陈晓东,等.汽车模拟碰撞吸能器的仿真分析及试验[J].江苏大学学报(自然科学版),2006,27(4):324-327.

[7] 张慧云,柳立志,杨斌,等.减速台车波形发生器的曲线复现及应用[J].汽车科技,2015(1):57-62.

[8] XU Fengxiang,WANG Chao.Dynamic axial crashing of tailor-welded blanks (TWBs) thin-walled structures with top-hat shaped section[J].Advances in Engineering Software,2016,96:70-82.

[9] MEHMET A G,MUHAMMED E C,BERTAN B,etal.The effect of geometrical parameters on the energy absorption characteristics of thin-walled structures under axial impact loading[J].International Journal of Crashworthiness,2010,15(4):377-390.

[10] JIMENEZ M,MARTINEZ J,FIGUEROA U,etal.Finite element simulation of mechanical bump shock absorber for sled tests[J].International Journal of Automotive Technology,2015,16(1):167-172.

[11] 尚福林,王子昆.塑性力学基础[M].西安:西安交通大学出版社,2011:9-13.

[12] 沈超.关于塑性应变能密度断裂准则研究[D].西安:西安理工大学,2013.

MotionandMechanicalPropertiesoftheCollisionProcessinVehicleCollisionTest

WANGJia-shun,ANQi

(SchoolofMechanicalandPowerEngineering,EastChinaUniversityofScienceandTechnology,Shanghai200237,China)

The paper took the vehicle collision test as the research object,analyzed the calculation method of the friction work and deformation energy of the block bar.Based on the principle of energy conservation,the energy balance model of the collision process is described,and the mathematical model is built to calculate the movement of the sled and the deformation of the block bar during the collision process,and a calculation method is proposed to solve this model by Matlab.With a specific example,the influences of the quality of sled,the initial collision speed,the center distance of the inner pin,and the cross section size of the block and so on,the displacement,collision force,speed and deceleration are studied,and some curves are obtained and analyzed.

collision test; deceleration device; mechanical modeling; motion properties; mechanical properties

1006-3080(2017)06-0863-08

10.14135/j.cnki.1006-3080.2017.06.017

2017-01-18

上海市设计学Ⅳ类高峰学科项目(DA17014)

王家顺(1992-),男,山东人,硕士生,研究方向为机械设计及理论。

安 琦,E-mail:anqi@ecust.edu.cn

TH113.2+2

A