爆破振动下地表建筑物振动位移研究

李洪梅，王小委，耿大新

（1.江西交通职业技术学院路桥工程系，江西南昌 330013；2.华东交通大学土木建筑学院岩土工程研究所，江西 南昌 330013）

爆破振动下地表建筑物振动位移研究

李洪梅1，王小委1，耿大新2

（1.江西交通职业技术学院路桥工程系，江西南昌 330013；2.华东交通大学土木建筑学院岩土工程研究所，江西 南昌 330013）

采用动力学分析方法结合拉氏变换及其逆变换，构建了爆破振动下地表建筑物振动位移解析表达式。以重庆市轨道交通一号线施工为例，计算发现爆破施工中隧道两侧余家湾水库附近房屋建筑发生振动位移大小达4 cm，处于非稳定状态，与实际较吻合。分析讨论了爆破药量、振动波主频率和建筑物墙体刚度三因素对振动位移的影响，发现在爆破药量和振动波主频率增加的情况下，建筑物振动位移呈增加趋势，但爆破药量对建筑物振动位移影响较振动波主频率大。建筑物墙体刚度能有效抑制振动位移的增加，但只在一定刚度范围内效果明显。

结构动力学；振动位移；拉氏变换；地表建筑物

随着人们对地下空间开采脚步的加快，地下工程施工对地质环境损伤破坏问题越来越严重，引起社会普遍关注。相关行业的学者及工程人员也做了深入研究，取得了较丰硕成果，如：李启发[1]分析了爆破地震波作用下边坡稳定性情况，发现边坡稳定性影响因素与爆炸能量、爆炸地震波传播形式及边坡自身性质有关，结论与实际相符；高文学等[2]从另外一个角度探讨了爆破开挖过程中边坡动力稳定性分析方法，并结合工程实例做了有限元数值模拟，结果表明采用缓冲爆破技术可有效降低爆破振动对边坡稳定性影响；陈兴泽等[3]研究了地下厂房开挖爆破地震反映谱特性，发现地下厂房开挖爆破振动反映谱具有明显放大效应；史秀志等[4-5]基于粗糙集模糊神经网络对爆破振动危害做了预测，显示了粗糙集模糊神经网络理论在预测中的优势，同时采用BDA模型预测了爆破振动对房屋建筑的破坏效应，为露天采矿爆破带来的振动效应提供了一种新预测方法；言志信等[6]探讨了爆破振动峰值速度的预报方法和Fourmap法，并采用人工神经网络预测了爆破振动峰值速度；陈博闻[7]采用量纲分析法建立影响爆破振动频率各物理量之间的函数关系，为爆破振动频率衰减规律的研究提供理论依据；许名标、彭德红[8]对边坡在爆破振动中的响应做了现场测试及ANSYS时程分析，发现在爆破规模较大时，振动速度可能沿高程出现放大效应，并提出应尽量采用没有放大效应或者放大效应较弱的爆破方式，以减小爆破振动，提高边坡在爆破动力作用下的稳定性；P K Singh[9]研究露天矿爆破开采振动效应，发现地下巷道顶部的振动效应明显高于巷道支柱，且在巷道口更甚；Reza Nateghi[10]对在建的Gotvand坝附近地下及地表爆破引起地面振动情况作量测，并按提出的模型预测了爆破振动对地表影响程度。上述研究成果虽深入揭示了地下工程施工对岩体损伤机理，但未涉及地表建筑物破坏问题，尤其对于地表建筑物振动位移研究国内外未见文献报导。

基于上述研究现状，本文拟采用动力学分析方法，并借助拉氏变换构建地上建筑物在爆破作用下的振动位移计算公式，相关研究成果可弥补国内外研究空白，也为地下工程施工及地表建筑物修建提供积极的指导作用，理论和实践意义重大。

1 爆破振动下等效加速度计算

爆源与建筑物相对位置如图1，以此为分析对象，建立爆破作用下建筑物振动加速度计算式。

目前对于爆破振动速度的一般计算途径都是采用回归拟合分析方法，为此，在缺乏实测数据的情况下，借助萨道夫斯基关于爆破振动峰值速度经验公式[11]，获取地面质点振动峰值速度，如式（1）：

式中：Vmax为质点振动峰值速度，m/s；Q为单段最大装药量，kg；R 为测点与爆源直线距离，m；K，α分别为场地系数和衰减系数，与爆破区域地质、爆破方法等因素有关，可参照《工程地质手册》和相关文献取值。

假定研究区域的振动由某一主频率控制，爆破振动峰值速度在水平和竖向分量有如下形式［12］：

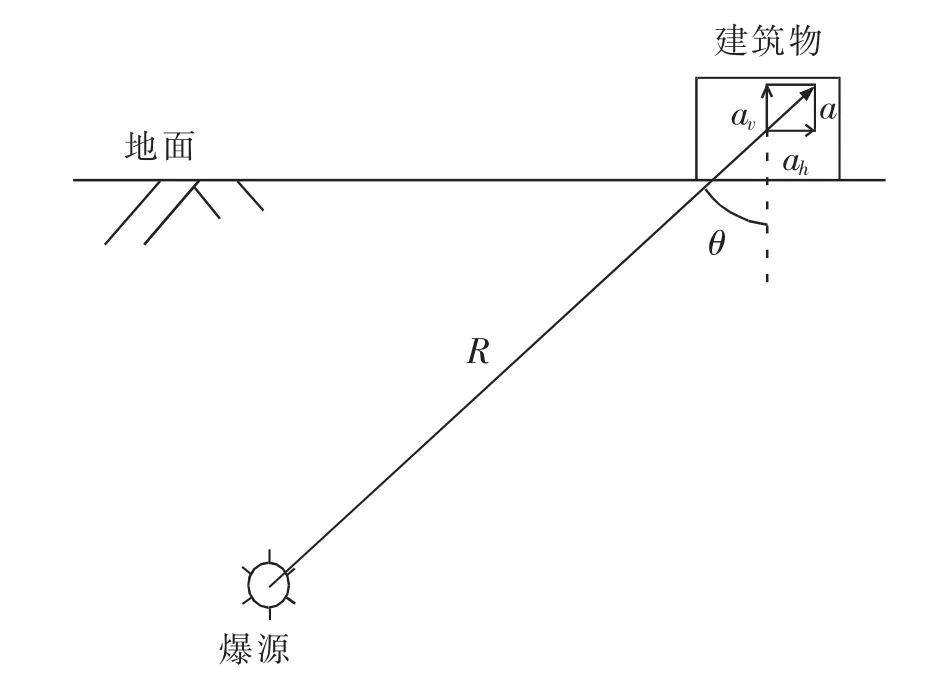
图1 爆源和建筑物相对位置简图Fig.1 Position between explosion source and surface building

式中：η为爆破振动衰减指数；ω为爆破振动波主频率，Hz；φ0为初相位，（°）。

将上式两端对时间t求导得振动加速度：

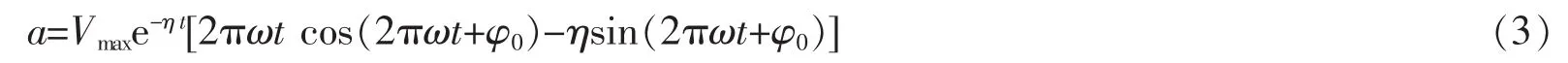
在简单考虑下，认为质点振动加速度方向与爆源和质点连线方向一致[13]，如图1所示。考虑到影响建筑物稳定性因素主要来自于水平向振动，因此，下面主要考虑在水平向振动条件下建筑物稳定性问题，振动加速度按式（4）计算。

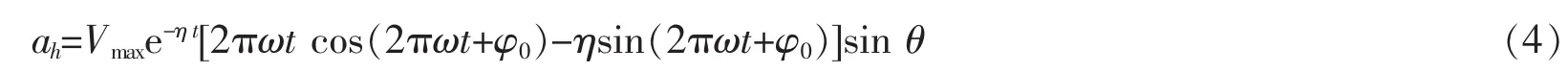
式中：θ为质点与爆源连线方向与竖向夹角，（°）。

2 建筑物的动力分析

按经典结构动力学分析方法，将建筑物动力分析模型简化为图2：

爆破振动引起地面水平运动用相对于固定参考系的结构基底位移ug（t）表示；建筑物总位移为 ut（t），相对于地面位移为 u（t），质量为 m，kg；建筑物变形引起相对运动产生弹性恢复力和阻尼力，弹性恢复系数和阻尼系数分别用k（kN/cm）和 c（kN·s/m）表示。

取隔离体分析，如图3，应用D’Alemert原理，得建筑物动力平衡方程：

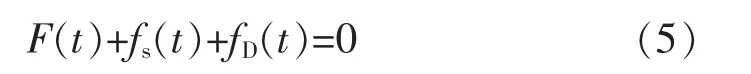
假设研究系统为线性系统，则有（6）：

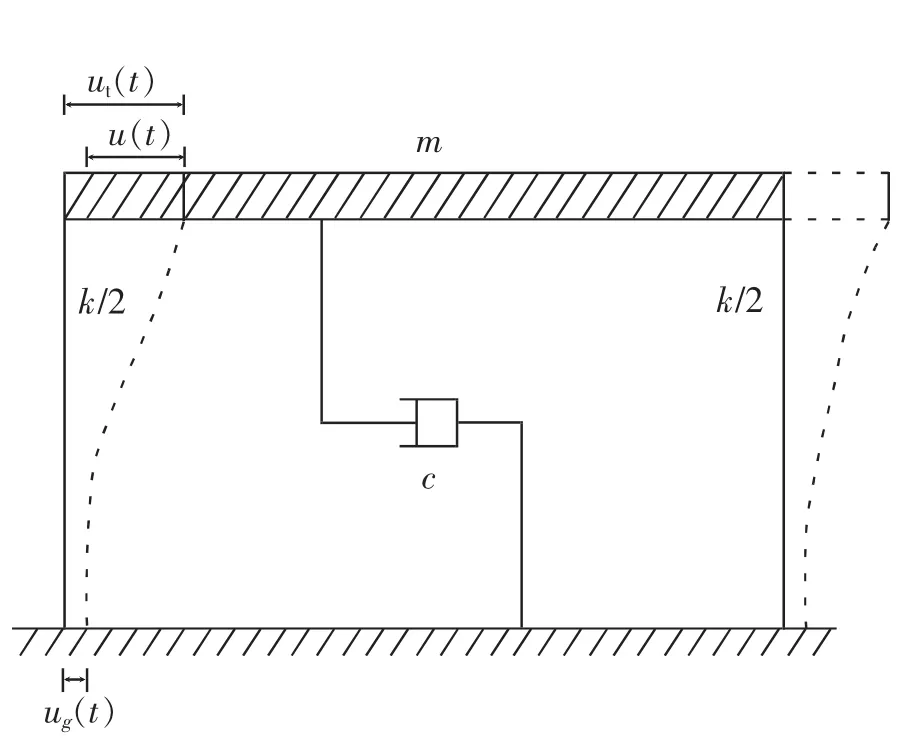
图2 建筑物动力分析模型Fig.2 Building’s dynamic analysis model

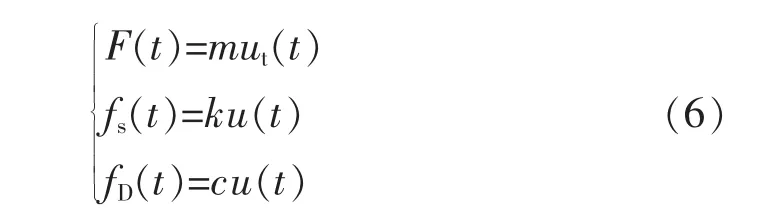
式中：F（t）为建筑物运动产生的惯性力；fs（t）为建筑物相对运动产生的弹性恢复力；fD（t）为建筑物相对运动产生的阻尼力。

考虑到 ut（t）=ug（t）+u（t），将式（6）代入式（5）得

mu（t）＋cu（t）+ku（t）=-mug（t） （7）

观察式(7)形式上特点，可以将右端视为施加在建筑物上的爆破振动等效荷载，因此有式(8)。令 A=c/m，B=k/m，C=2πωK （Q1/3/R)αsin θ，D=-K（Q1/3/R）αsin θη，将式（8）简化为式（9）：

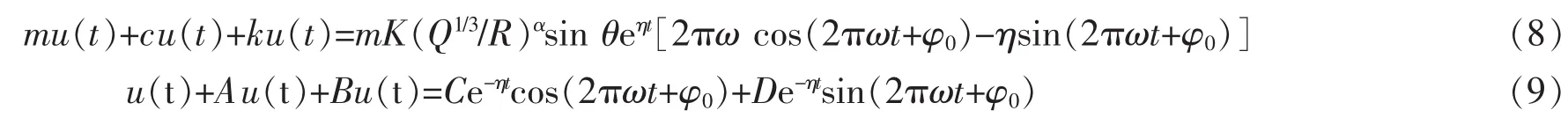
针对一般性二阶常微分方程，已无相应求解公式，因此采用积分变换的一种变换——拉氏(Laplace)变换求解上述二阶常微分方程。

对式（9）两端同时作关于变量t的拉氏变换有：

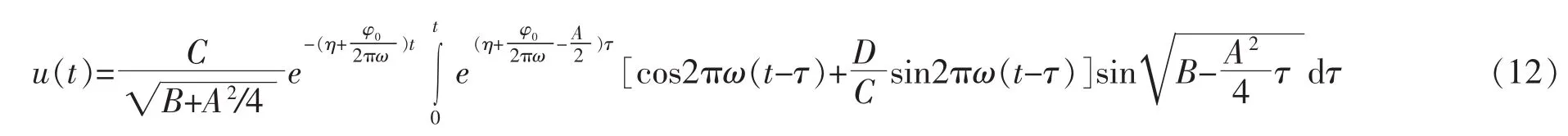
至此，地上建筑物在爆破振动作用下相对于地面的水平位移u（t）求解完毕。依据u（t）大小，查找《爆破安全规程》相关规定，可以判断建筑物稳定状况。

3 实例分析

3.1 中梁山隧道余家湾水库附近建筑物振动位移计算

中梁山隧道是重庆市轨道交通一号线(沙坪坝～大学城段)双碑北站～赖家桥站区间的一部分，两侧与高架桥线路连接，隧道进洞位于沙坪坝区中冶十八局预制构件厂背后中梁山东麓山坡，出洞口位于陈家湾蕉园村常五间社中梁山西麓山坡上。根据重庆一三六地质矿产有限责任公司调查，发现在轨道交通一号线施工过程中，隧道两侧周围出现房屋开裂、地面塌陷等现象，且房屋变形主要集中在余家湾水库四周，位于观音峡背斜西翼，隧道K26+200～K27+900 m段两侧，靠近隧道出口端施工点[14-15]，隧道开挖地质剖面如图4。

按调查报告，房屋变形严重地段与轨道交通一号线施工放炮点垂直距离在170 m范围内，水平距离在250 m范围内，故爆心距R=302 m，爆源和建筑物质点连线方向与竖直向夹角θ=56°，如图5所示。总装药量282 kg，依据隧道开挖场地工程地质条件结合相关文献，查阅工程地质手册，场地系数K=600，衰减系数α=1.2，爆破衰减指数η=10，爆破振动波主频ω=20 Hz，φ0=0°，弹性恢复系数k=170 kN/cm，阻尼系数c=275 kN·s/m，建筑物按单层砌体结构考虑，建筑尺寸取10 m×10 m，总质量m≈1.2×105kg。将以上数据代入计算：

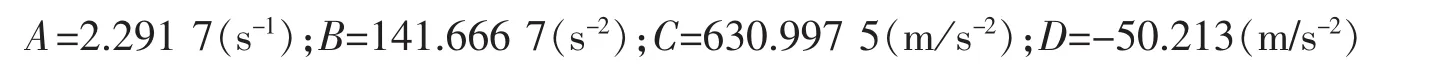
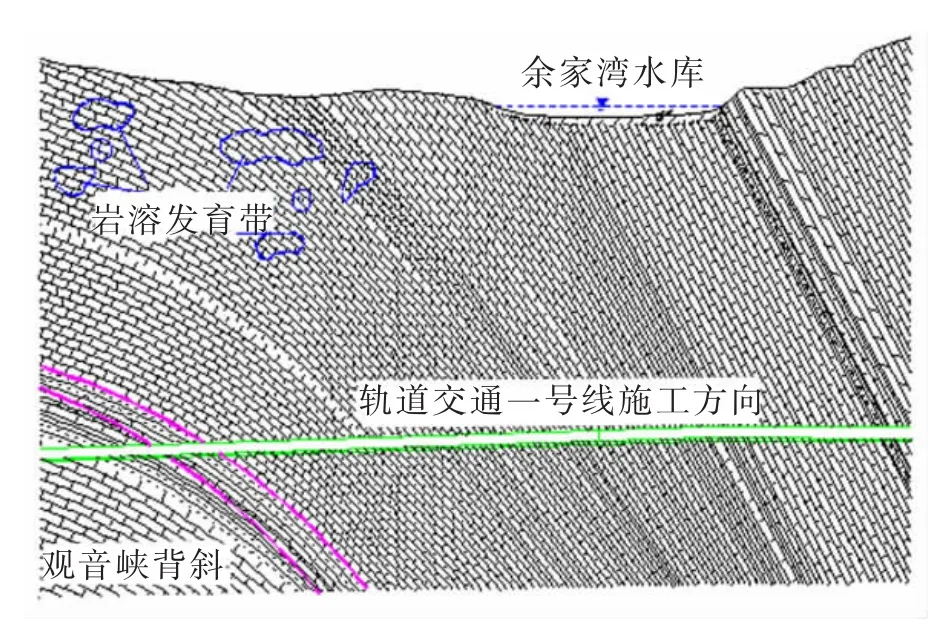
图4 隧道开挖地质剖面图Fig.4 Geological cross-sectional view

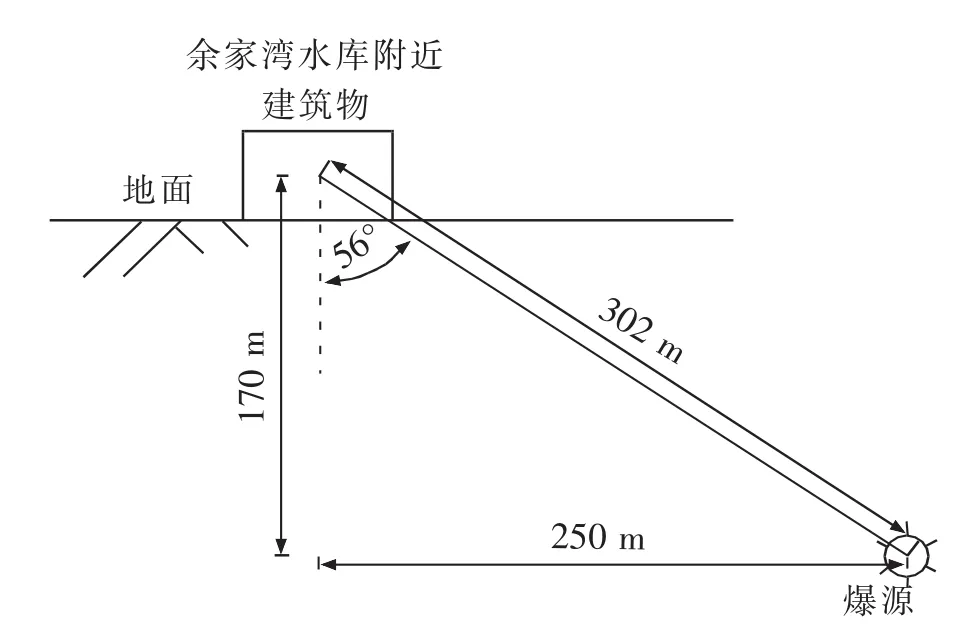
图5 余家湾水库附近建筑物与爆源相对位置图Fig.5 Relative position between explosion source and surface building near Yujiawan Reservoir

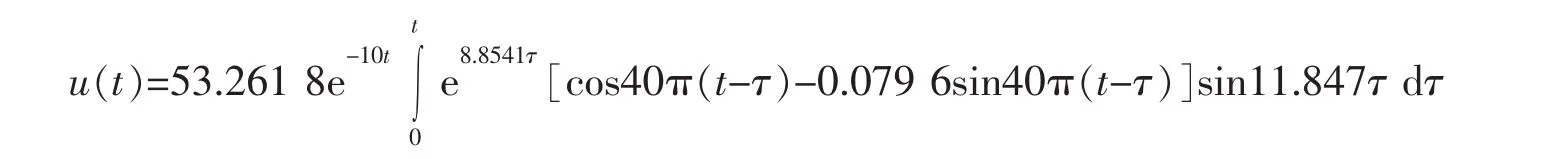
为直观反映建筑物在爆破振动下与地面产生的相对位移，将振动位移函数u（t）随时间变化曲线在数值计算软件matlab中绘出，如下图6示。由曲线知，在爆破振动作用下，隧道K26+200～K27+900 m段两侧建筑物发生相对于地面位移达4 cm，按《爆破安全规程》，在如此大错动位移作用下，建筑物稳定性无法保证，是不允许的，这就印证了调查发现的隧道两侧周围出现房屋开裂这一事实。

因此，上述方法用于预测建筑物在爆破振动下的错动位移是可行的。

3.2 讨论

下面做相关讨论，讨论装药量、爆破振动波主频率以及墙柱侧向刚度（弹性恢复系数）对建筑物振动位移影响，设计参数如表1，其它参数参考中梁山隧道余家湾水库附近建筑物振动位移计算部分。将侧向刚度系数和振动波主频率进行组合，即（k，j），共25种组合工况，具体如表2所示。

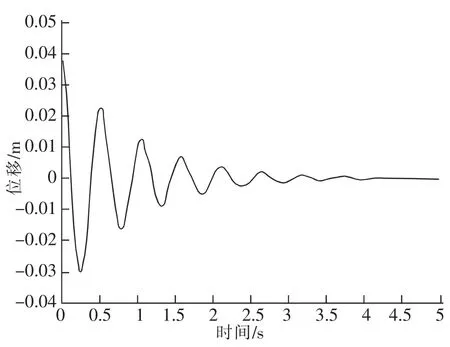
图6 爆破振动下地表建筑物位移时程曲线Fig.6 Surface building displacement-time curve under blasting vibration

表1 设计参数Tab.1 Design parameter

由于设计情况较多，手算时间长，因此在matlab中编制程序做运算，计算结果如图7所示。

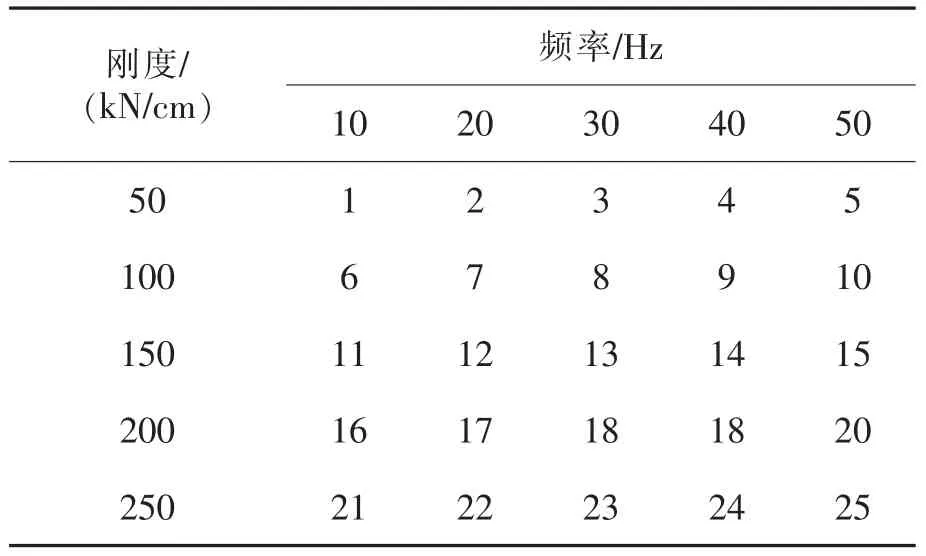
表2 振动波主频率和墙体刚度组合工况表Tab.2 Combination conditions of main frequency and building’s stiffness

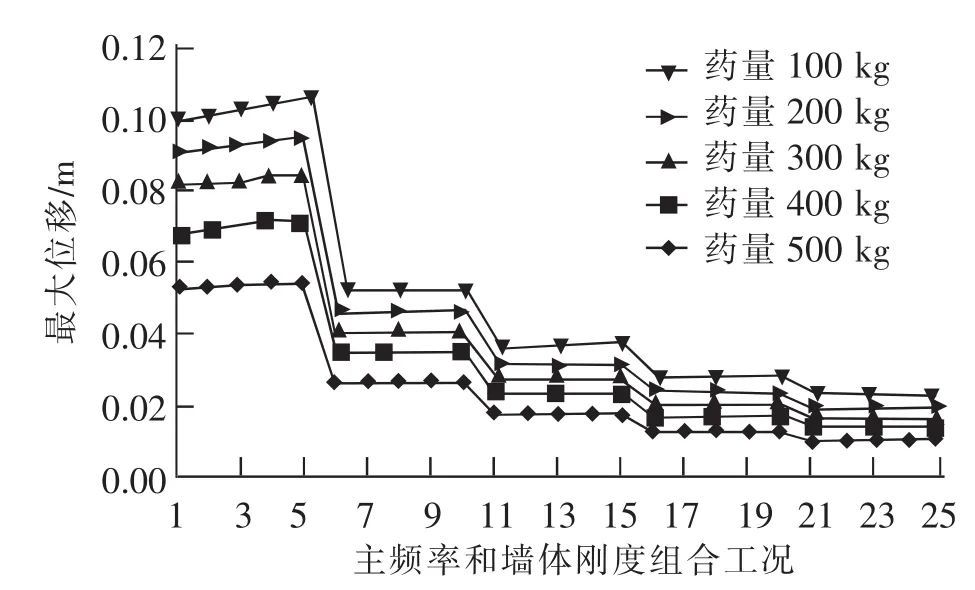
图7 不同药量下建筑物最大位移曲线图Fig.7 Building’s maximum displacement curve in different blasting dosage

分析图7可知：考虑单一因素前提下，建筑物在爆破作用中振动位移随爆破药量的增加呈明显增加趋势，但增加速率却随药量的增加而减小。

在爆破药量和墙体刚度不变的情况下，分析振动波主频率对振动位移影响。以药量300 kg，墙体刚度150 kN/cm为例，振动位移随时间变化曲线如下图8。分析图8可知：在主频率增加的情况下，振动位移有所增加，且呈直线增长，但不是很明显；主频率增加，导致曲线两波峰之间间距缩小，即“振动周期”减小，曲线直观上更具波动性。

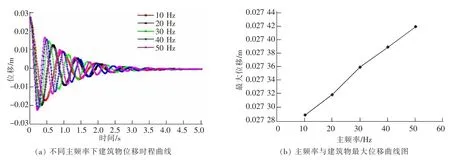
图8 主频率对错动位移的影响分析图Fig.8 Influence analysis of main frequency on building’s displacement

在爆破药量和主频率不变的情况下，分析墙体刚度对振动位移影响。以药量300 kg，主频率30 Hz为例，振动位移随时间变化曲线如下图9。分析图9可知：在墙体刚度增加的情况下，振动位移呈抛物线型下降，可见，墙体刚度对振动位移影响较大，能有效抑制建筑物振动位移的增加。

4 结论

本文针对地下工程爆破施工，研究了爆破施工下地表建筑物振动位移，主要结论如下：

1）运用动力学分析方法，推导了建筑物振动位移满足的微分方程，采用拉氏变换及其逆变换得到了振动位移积分形式的求解公式。

2）以重庆市轨道交通一号线中梁山隧道施工为例，计算了爆破施工过程中，隧道两侧余家湾水库附近房屋建筑发生振动位移大小可达4 cm，与实际调查发现的大面积房屋开裂现象较吻合，验证了公式的合理性。

3）对爆破药量、振动波主频率和建筑物墙体刚度做单因素敏感性分析，发现建筑物振动位移随爆破药量和振动波主频率的增加呈增加趋势。

4）墙体刚度的增加可以有效抑制建筑物振动位移增长，保证建筑物安全，但在刚度达到一定数值后抑制效果不明显。

本文构建的振动位移计算公式弥补了国内外研究空白，且相关结论对地下工程施工及地表房屋建设有积极指导作用，理论和实践意义重大。

[1]李启发.爆破地震波对岩质边坡稳定性的影响[J].爆破，1995，12（3）：1-4.

[2]高文学，刘宏宇，刘洪洋，等.爆破开挖对路堑高边坡稳定性影响分析[J].岩石力学与工程学报，2010，29（1）：2982-2987.

[3]陈兴泽，杨兴国，李洪涛，等.地下厂房开挖爆破地震反应谱特征研究[J].工程爆破，2012，18（1）：44-47.

[4]史秀志，林大能，陈寿如.基于粗糙集模糊神经网络的爆破振动危害预测[J].爆破与冲击，2009，29（4）：401-407.

[5]史秀志，周健，杜坤，等.爆破振动对民房破坏效应预测的BDA模型及应用[J].振动与冲击，2009，29（7）：60-65.

[6]言志信，言浬，江平，等.爆破振动峰值速度预报方法探讨[J].振动与冲击，2010，29（5）：179-182.

[7]陈博闻.基于量纲分析的爆破振动频率公式[J].水利水电技术，2012（2）：54-57.

[8]许名标，彭德红.边坡爆破振动测试及响应规律ANSYS时程分析[J].岩石力学与工程学报，2012，31（A01）：2629-2635.

[9]P K SINGH.Blast vibration damage to underground coal mines from adjacent open-pit blasting[J].International Journal of Rock Mechanics&Mining Sciences，2002，39：959-973.

[10]REZA NATEGHI.Prediction of ground vibration level induced by blasting at different rock units[J].International Journal of Rock Mechanics&Mining Sciences，2011，48：899-908.

[11]张忠伟，朱传云，姜清辉，等.引水隧洞爆破开挖对邻近建筑物的振动影响分析[J].爆破，2004，21（1）：82-85.

[12]许洪涛，卢文波，周创兵，等.基于时程分析的岩质高边坡开挖爆破动力稳定性计算方法[J].岩石力学与工程学报，2006，25（11）：2213-2219.

[13]何蕴龙.岩质边坡施工爆破振动加速度近似计算方法[J].岩石力学与工程学报，1996，15（1）：19-25.

[14]王明年，翁汉名，关宝数.我国3条高速公路隧道污染状况调查[J].环境科学，1997，18（3）：50-55.

[15]曾艳华，李永林，何川，等.隧道通风网络及调节[J].西南交通大学学报，2003，38（2）：183-187.

Study on Surface Building Vibration Displacement under Blasting Vibration

Li Hongmei1，Wang Xiaowei1，Geng Daxin2
（1.Road and Bridge Engineering Department,Jiangxi V&T College of Communication,Nanchang 330013，China；2.Geo-technical Engineering Research Institute,School of Civil Engineering and Architecture,East China Jiaotong University,Nanchang 330013,China）

The analytical expression of surface building vibration displacement was established under blasting vibration by using dynamic analysis methods and Laplace transform.Taking Chongqing Rail Transit Line 1 as an example,the calculation shows that the vibration displacement of buildings near Yujiawan Reservoir reaches 4cm under blast working,which,in an unsteady state,coincides with the actual situation.The effects of blasting dosage,main frequency of vibration wave and building’s stiffness on vibration displacement were discussed and the research results show that with the increase of blasting dosage and main frequency of vibration,building vibration displacement also increases;however,the effect of blasting dosage on vibration displacement is bigger than that of main frequency of vibration wave;the building’s stiffness can,within a certain range,control vibration displacement effectively.

structural dynamics； vibration displacement； Laplace transform； surface building

（责任编辑 王建华）

TD235.1

A

1005-0523（2017）06-0038-07

2017－06－03

李洪梅（1987—），女，助理讲师，研究方向为岩石力学及地下工程地质环境保护。