SD型模数式伸缩缝耦合动力学研究

程海根，梁宝明，占小剑，陈博文

（华东交通大学土木建筑学院，江西 南昌 330013）

SD型模数式伸缩缝耦合动力学研究

程海根，梁宝明，占小剑，陈博文

（华东交通大学土木建筑学院，江西 南昌 330013）

以SD型模数式伸缩缝为研究对象，运用有限元分析软件ABAQUS对SD型模式伸缩缝进行耦合(竖向和水平)动力学研究。其中，建立了完整的耦合动力学理论模型，模拟在行驶的汽车通过伸缩缝时，伸缩缝中梁竖向和水平向振动响应特性。研究结果表明：不考虑车辆制动力以及不同车速情况下，伸缩缝中梁竖向振动位移与水平振动位移之间几乎没有什么影响。因此，对伸缩缝竖向和水平向振动响应研究时可以单独进行研究，从而可以简化研究，提高效率。制动力对伸缩缝水平振动位移影响比较大。如果考虑制动力的影响，水平振动位移的增大会对伸缩缝结构产生不利的影响。不考虑制动力情况下，采用德国规范分析得到的水平振动位移最大值为0.235 mm，采用我国规范并忽略制动力下分析得到最大水平振动位移几乎接近于零；而最大竖向振动位移比按照我国规范并忽略制动力影响的条件下分析得到的小21%。在不同速度80 km/h，120 km/h条件下，采用德国规范分析得到的伸缩缝最大竖向振动位移与我国规范分析得到的相比分别小16%和19%。

SD型模数式伸缩缝；有限元分析软件；耦合动力学；振动响应特性；制动力；德国规范

近年来，随着我国交通运输行业的快速发展，大跨度的桥梁建设显著增多，大位移桥梁伸缩缝的需求也随之增大。桥梁伸缩缝要承受因温度等原因引起的梁长度变化的影响和车辆载荷的反复作用，加之使用环境比较恶劣，又长期暴露在空气中，所以它是桥梁结构最易遭到破坏而又较难修补的装置。

SD型伸缩装置又名美国沃特森（Wotson）伸缩装置[1]，属于模数式伸缩装置的一种，均以80 mm为单元模数，其中包括两种构造型式：箱型构造和鸟形构造。该伸缩装置的中梁钢、边梁钢均采用低碳优质耐腐蚀钢材制造。伸缩装置的主要部件异型钢孔型采用数控机床车削而成，孔型标准，密封橡胶条耐久可靠且防水性能好。且该伸缩装置具有良好的位移控制系统和稳定的支承系统等特点，故其在高速公路桥梁中应用比较广泛。

车辆通过伸缩缝时，将作用在伸缩缝装置顶面的载荷分为两个部分：竖向载荷和水平载荷。目前国内外主要对车辆通过SD型伸缩装置时的竖向振动响应和水平向振动响应特性进行了研究[2-3]，但对SD型伸缩装置进行耦合动力学仿真几乎没有研究。本文将运用有限元分析软件ABAQUS[4-5]对SD型模数式伸缩缝进行耦合动力学仿真研究，对比3种不同工况条件下中梁的最大竖向位移和水平向位移，从而为SD型模数式伸缩缝的设计和研发提供了一定的数据。

1 SD型模数式伸缩缝结构分析

1.1 SD型模数式伸缩缝构造图分析和结构参数

SD型模数式伸缩装置主要由边梁、中梁、横梁、位移控制系统、密封橡胶带、锚固系统等组成，其中梁与支撑横梁采用刚性连接，结构简图如图1所示。

图1 SD型模数式伸缩装置构造图Fig.1 The structure of SD-type modular expansion device

根据参考资料与计算结果，伸缩缝模型的技术参数如表1所示。

1.2 方程建立

当车辆通过伸缩缝时，第f号中梁（f=1～5）的振动方程[6]表述如下：

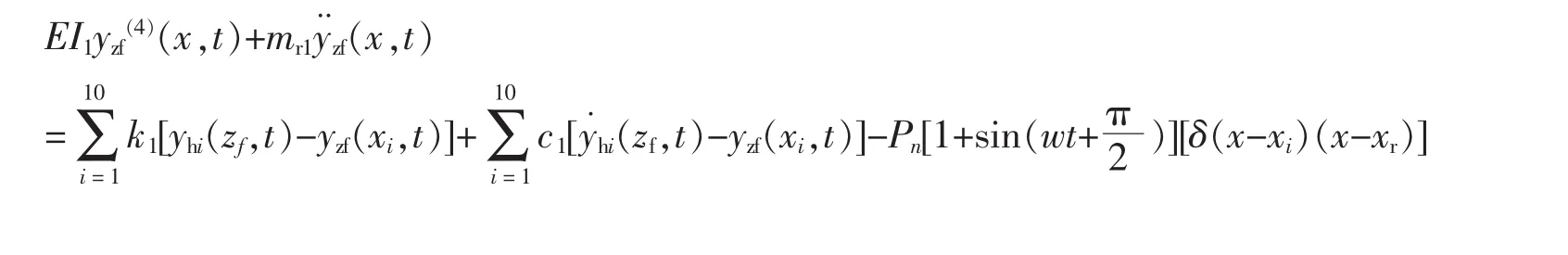
式中：I1为中梁的截面惯性矩，m4；mr1为中梁单位长度的质量，kg；Pn为轮压载荷，N；k1为弹性支撑的刚度系数，N/m；为 f号中梁在位置 x 处的竖向加速度，mm/s；yhi（zf，t），（zf，t）为 i号横梁的竖向位移（mm），和速度，mm/s；yzf（xi，t），（xi，t）为 f号中梁竖向位移（mm），和速度，mm/s；yzf（4）为 f号中梁竖向位移对位置 x 的 4阶导数；这样就建立了完整的动力学方程。

1.3 模型的建立

SD型伸缩装置的中梁钢、边梁钢均采用低碳优质耐腐蚀钢材制造[7]。其中中梁钢、边梁刚、支撑横梁、支撑箱采用梁单元模拟，滑动支撑、压紧支撑、剪切弹簧采用弹簧阻尼单元模拟，中梁和横梁之间采用刚性连接。SD型模数式伸缩缝有限元模型如图2所示。

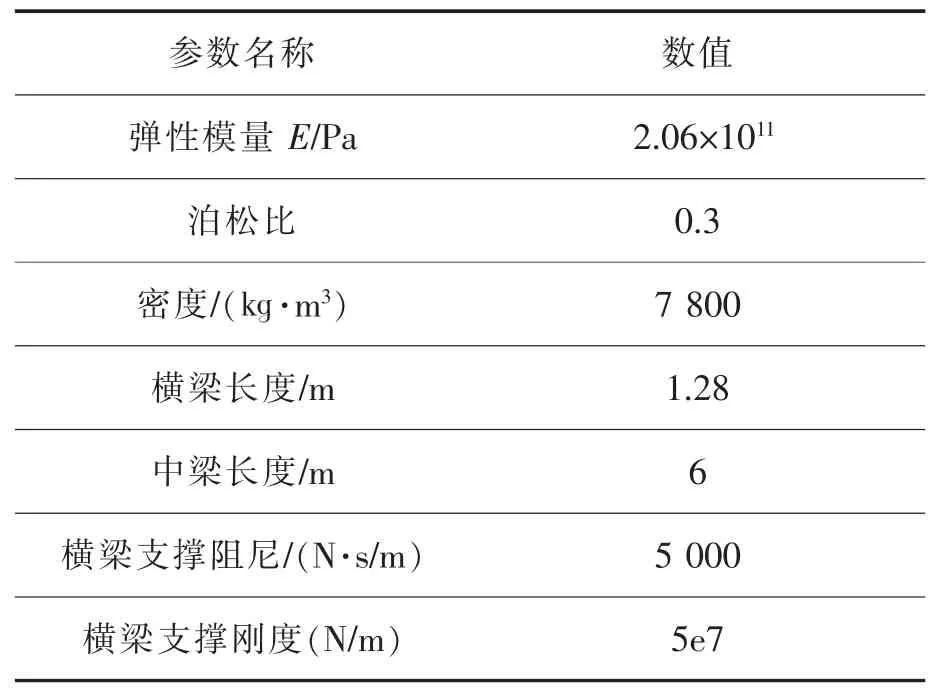
表1 SD型伸缩缝结构参数Tab.1 Structural parameters of SD-type expansion joints

图2 SD型模数式伸缩缝有限元模型Fig.2 SD modular expansion joint finite element model

1.4 载荷分析及加载方案

车轮荷载通过伸缩缝时，对中梁既有竖向荷载，同时也有水平荷载。参考我国 《桥涵设计通用规范》（JTG D60-2004）[8]、《现代桥梁伸缩装置》等,作用在伸缩装置顶面的疲劳载荷主要为竖向疲劳载荷[9]。竖向疲劳载荷：车辆载荷后轴重力标准值140 kN，在不考虑制动力的情况下，汽车单组轮作用下的竖向疲劳载荷大小为101.5 kN，水平疲劳载荷主要为克服风荷载产生的摩擦力大小为21 kN。考虑制动力的情况下，汽车单组轮作用下的竖向疲劳载荷大小为101.5 kN；水平疲劳载荷主要为汽车制动力大小为21 kN。参考德国《公路桥、人行桥不透水伸缩装置技术交付及验收规范》（TP/TP-FU92）第5.2条规定[10]，汽车单组轮作用下的竖向疲劳载荷大小为58.8 kN,水平疲劳载荷大小为4.38 kN。

综合以上载荷分析，本文将分以下3种不同的工况分别进行研究，如表2所示。

表2 载荷分析Tab.2 Load analysis

2 SD型模数式伸缩缝耦合动力学响应分析

本文选定缝宽为80 mm的SD型伸缩缝为研究对象，考虑在最不利的工况条件下，即汽车其中一组单组轮载荷恰好压在两横梁的中间位置处，采用以上3种不同工况条件下,当汽车以速度为80 km/h、120 km/h分别通过伸缩缝时，3号中梁在该单组轮作用位置处的位移响应图分别如图3所示。

2.1 工况a条件下伸缩缝动力学响应分析

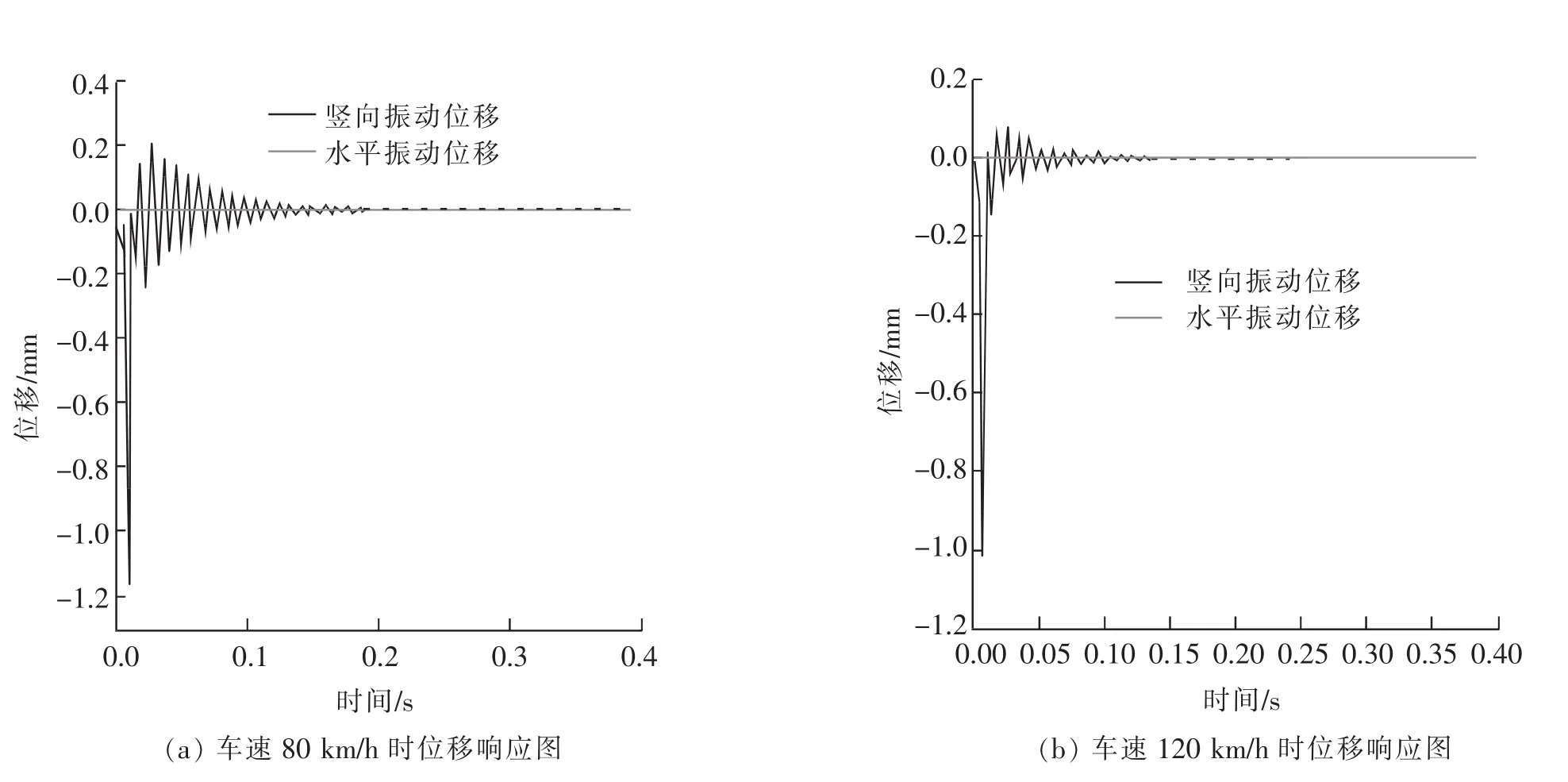
图3 不同车速下3号中梁的位移响应图Fig.3 Displacement response diagram of No.3 center beam at different speeds

由图3及图4可知：不同车速下，伸缩缝中梁的竖向振动位移波动比较大，而水平振动位移几乎为零，说明在不考虑车辆制动力情况下，伸缩缝中梁的竖向振动位移与水平振动位移之间几乎没什么影响。因此，当不考虑车辆制动力情况时，可以对伸缩缝竖向和水平向振动响应单独进行研究。

2.2 工况b条件下伸缩缝动力学响应分析

虽然在进行伸缩缝疲劳计算时，大多数情况下我们不考虑车辆在伸缩缝处制动这种情况。但是，随着汽车数量日渐增多，汽车在伸缩缝处制动的频率也在增大。因此，研究汽车在伸缩缝处制动伸缩缝中梁的动力学响应就显得很有意义。不同车速80，120 km/h下，考虑汽车制动力情况下，伸缩缝3号中梁的位移响应图如图5（a）所示。

图4 3号中梁最大竖向与水平向振动位移随车速变化Fig.4 The maximum vertical and horizontal vibration displacement of No.3 center beam changes with the vehicle speed

图5 不同车速下3号中梁的位移响应图Fig.5 Displacement response diagram of No.3 center beam at different speeds

由图5及图6可知：考虑制动力的情况下，伸缩缝中梁水平振动位移比不考虑制动力情况下增大比较明显；相同速度情况下，最大竖向位移也比不考虑制动力情况下大；当速度大于50 km/h时，随着速度的增大，竖向振动位移和水平振动位移都呈现增大趋势，在速度为100 km/h处达到最大值，然后随着速度的增大逐渐减小。说明制动力对伸缩缝水平振动位移影响比较大。如果考虑制动力的影响，水平振动位移的增大会对伸缩缝结构产生不利的影响。

2.3 工况c条件下伸缩缝动力学响应分析

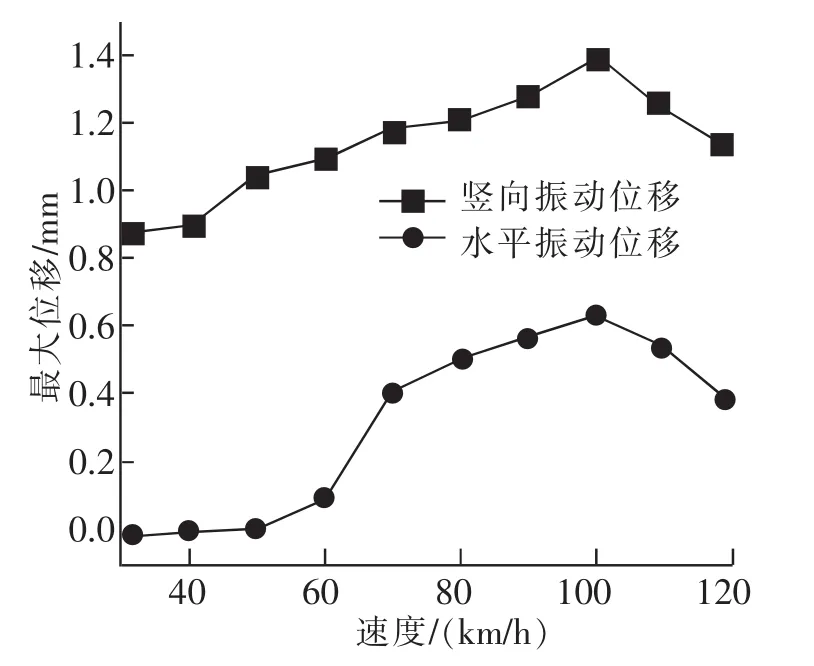
图6 3号中梁最大竖向与水平向振动位移随车速变化Fig.6 The maximum vertical and horizontal vibration displacement of No.3 center beam changes with the vehicle speed

德国规范规定：作用在伸缩缝上的竖向疲劳载荷的大小为轴重力加冲击力的0.6倍大小为117.6 kN。因此，单组轮上的载荷大小为58.8 kN。水平疲劳载荷为静水平载荷的0.25倍大小为8.75 kN，所以单组轮作用位置处的水平疲劳载荷大小为4.38 kN。工况d条件下，汽车以不同速度通过伸缩缝时，伸缩缝3号中梁的振动位移响应图如图7所示。

图7 不同车速下3号中梁的位移响应图Fig.7 Displacement response diagram of No.3 center beam at different speeds

由图7及图8可知：采用德国规范分析得到的伸缩缝最大竖向振动位移比工况a条件下分析得到的小21%；水平振动位移最大值为0.235 mm，而工况a条件下分析得到最大水平振动位移几乎接近于零。在不同速度80，120 km/h条件下，采用德国规范分析得到的伸缩缝最大竖向振动位移与工况a条件下分析得到的相比分别小16%和19%。

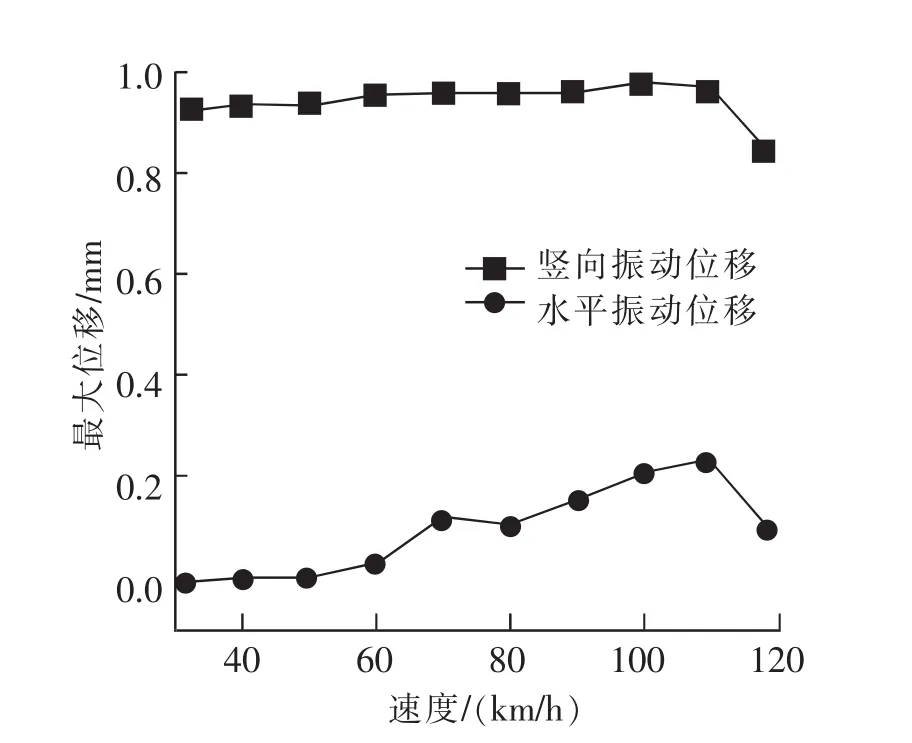
图8 3号中梁最大竖向与水平向振动位移随车速变化Fig.8 The maximum vertical and horizontal vibration displacement of No.3 center beam changes with the vehicle speed

3 结论

通过对SD型模数式伸缩缝进行了简化分析，建立了完整的耦合动力学模型。得到了在不同工况条件下，汽车以不同速度通过伸缩缝时，伸缩缝竖向和水平向的动力学响应特性，结论如下：

1）不考虑车辆制动力及不同车速情况下，伸缩缝中梁竖向振动位移与水平振动位移之间几乎没有什么影响。因此，不考虑车辆制动力情况下，对伸缩缝竖向和水平向振动响应研究时可以单独进行研究。从而可以简化研究，提高效率。

2）制动力对伸缩缝水平振动位移影响比较大。如果考虑制动力的影响，水平振动位移的增大会对伸缩缝结构产生不利的影响。

3）不考虑制动力情况下，当汽车以不同速度80，120 km/h通过伸缩缝时，采用德国规范分析得到的伸缩缝最大竖向振动位移与我国规范分析得到的相比分别小16%和19%。

[1]阳初.桥梁伸缩装置损伤分析和选型应用[D].华南理工大学，2014：41-42.

[2]JIRI STRAKKY.Sress-Ribbon Pedestrian Bridges Supported by Arches[J].Concrete International Farming ton Hills，2010：79-88.

[3]ERIC ANCICH.Dynamic Design of Modular Bridge Expansion Joints by the Finite Element[R].IABSE Symposium Report，2007：155-168.

[4]庄茁，由小川，廖剑晖，等.基于ABAQUS的有限元分析与应用[M].北京：清华大学出版社，2009：151-169.

[5]王恩成.利用有限元分析方法控制桥梁施工[J].公路工程，2010，35（4）：126-129.

[6]衡亚霖，王少华，张露，等.大位移桥梁伸缩缝垂向振动理论研究[J].机械设计与制造，2014（11）：39-42.

[7]张一卓.桥梁伸缩装置疲劳破坏分析及寿命估算[D].西安：长安大学，2005：26-35.

[8]JTGD60-2004，公路桥涵设计通用规范[S].北京：人民交通出版社，2004.

[9]张一卓.桥梁伸缩装置疲劳破坏分析及寿命估算[D].西安：长安大学，2005：17-19.

[10]严情木.大位移桥梁伸缩缝动力学分析[D].成都：西南交通大学，2013：8-9.

Research on the Coupling Kinetics of SD Modular Expansion Joint

Cheng Haigen，Liang Baoming，Zhan Xiaojian，Chen Bowen
（School of Civil Engineering,East China Jiaotong University,Nanchang 330013,China）

Taking SD modular expansion joint as the research object,this paper studied the vertical and horizontal coupling dynamics of SD modular expansion joint by using the finite element analysis software ABAQUS.A complete model of coupling dynamics was established to simulate the vertical and horizontal vibration response characteristics of the center beam of a moving car through the expansion joint.The results show that the vertical vibration displacement and horizontal vibration displacement of the center beam does not influence each other beyond vehicle braking force and speed.Therefore,the study on the vertical and horizontal vibration response of the expansion joints can be studied independently to simplify the research and improve efficiency.The braking force has larger influence on the vibration displacement of the expansion joint.Taking the influence of braking force into consideration,the increase of horizontal vibration displacement would have a negative effect on the expansion joint structure.Without considering the braking force,the maximum value of horizontal vibration displacement is 0.235 mm under Germany's specification and the maximum value of horizontal vibration displacement nearly approaches zero under China’s specification;however,the maximum vertical vibration displacement is 21 percent smaller than that of the analysis under the conditions of China's specification.Under the condition of 80 km/h and 120 km/h,the maximum vertical vibration displacement of the expansion joints obtained by German specification was 16%and 19%respectively smaller than that of China’s specification.

SD modular expansion joint； finite element analysis software； coupling dynamics； vibration response characteristics； braking force； Germany’s specification

（责任编辑 王建华）

U443.35

A

1005-0523（2017）06-0060-06

2017－08－07

国家自然科学基金项目（51068005）

程海根（1971—），男，教授，研究方向为桥梁伸缩缝动力学特性研究。